Ti3C2TxMXeneのその場高圧X線回折およびラマン分光法による研究
要約
Ti 3 の格子安定性とフォノン応答 C 2 T x 高圧のMXeneは、その機械的および熱的特性を完全に理解するために重要です。ここでは、その場での高静水圧X線回折(XRD)とラマン分光法を使用して、Ti 3 の格子変形とフォノン挙動を研究します。 C 2 T x MXene。 XRDスペクトルは、26.7GPaの圧力まで相転移が発生しないことを示しています。 a に沿った弾性定数 格子定数は378GPaと計算されました。高圧で得られたラマンスペクトルでは、面外フォノンモード( A 1g 〜210、〜504、〜711 cm -1 )圧力の増加に伴って単調なブルーシフトを示します。これら3つのモードのグリュナイゼンパラメーターは、それぞれ1.08、1.16、および0.29と計算されました。これらの結果は、Ti 3 の基本的な特性データを充実させます。 C 2 T x MXeneであり、この新しい素材をさらに理解するのに役立ちます。
背景
グラフェン[1]と遷移金属ジカルコゲナイド(TMD)[2,3,4,5]の10年間の集中的な研究の後、2次元(2D)金属炭化物(MXenes)は、その並外れた性質のために最近大きな注目を集めています。電気的特性[6、7]。 Ti 3 C 2 MXeneは、ファンデルワールススタック構造の層状材料であり、各層には3つのTi原子平面に挟まれた2つの炭素原子平面が含まれています。 Ti 3 のエネルギーバンド構造 C 2 MXene、伝導帯はΓ点で価電子帯に接触します。これは、Ti 3 であることを示しています。 C 2 MXeneはハーフメタリック素材です[8]。さらに興味深いことに、Ti 3 のバンド構造 C 2 Mxeneは、–F、–O、–OH [9]などの表面官能基(式では「T」と注釈が付けられています)[8]によってわずかに開くことができます。これらの官能基は、M n の溶液エッチングで生成されます。 AlC n + 1 フェーズ[9]は、Ti 3 を形成します。 C 2 T x 調整可能な電気的特性を備えたMXene。 Ti 3 の電気伝導率 C 2 T x MXeneは4.2×10 -4 と測定されました S / m [10]、これはほとんどのTMDよりも優れています。現在まで、Ti 3 C 2 T x MXeneは、高度なスーパーキャパシタ[11]、リチウム電池[12]、電磁シールド[10]、抗菌[13] 、での潜在的な用途を示しています。 と発光[14]。
高い導電性に加えて、Ti 3 の弾性特性 C 2 T x MXeneも注目を集めています。理論計算では、この極薄炭化物のヤング率は約500GPaと高いと予測されています[15、16、17]。 Lipatov etal。最近、ナノインデンテーションを使用して、単分子層Ti 3 のヤング率を決定しました。 C 2 T x MXeneは330Gpaでした[18]。これらの値は、MoS 2 の値よりもはるかに高くなっています。 [18]そして単層グラフェン[19]のものに匹敵します。最近、Ghidiu等。 Ti 3 の高圧X線回折(XRD)スペクトルを測定しました C 2 T x MXeneは最大3GPaで、相転移は観察されませんでした[20]。ただし、参照でロードされた圧力として。 [20]が低すぎたため、Ti 3 の相安定性と格子変形 C 2 T x 高圧での状態はまだ不明です。
ラマン分光法は、グラフェン[21]やTMD [2]などの2D材料の結晶構造とフォノン振動を調査するための有用な非破壊ツールとして機能します。 Ti 2 の組成 CT x [22]およびTi 3 の相安定性 C 2 T x さまざまなアニーリング条件でのMxene [10]は、共焦点ラマン測定を使用して調べることができます。最近、Ti 3 のフォノン分散 C 2 T x MXeneは、Huらによって理論的に計算されました。 [23、24]、したがって、この材料のラマンスペクトルのさらなる理解を可能にします。ただし、Ti 3 の高圧ラマン分光法 C 2 T x まだ不足しています。さらに、Ti 3 のフォノン応答 C 2 T x 圧力の関数としては不明です。
この論文では、Ti 3 を用意しました。 C 2 T x フレークを薄くし、26.7GPaまでの圧力依存XRDおよびラマンスペクトルを測定しました。 Ti 3 の弾性定数 C 2 T x Murnaghan方程式によるXRD回折ピークシフトから計算されました。面外フォノンの正のグリュナイゼンパラメーターは、それらの圧力依存ラマンシフトと格子パラメーター変形比から得られました。得られた結果は、Ti 3 の機械的およびフォノン振動挙動のさらなる理解に役立ちます。 C 2 T x MXene。
結果と考察
高圧測定を行う前に、まず、剥離したTi 3 の基本的な材料特性を調査しました。 C 2 T x Mxeneフレーク。剥離したTi 3 の光学画像 C 2 T x Si / SiO 2 に堆積したフレーク (300 nm)基板を図1aに示します。剥離したフレークには薄緑色のコントラストが見られます。ミランダらによって報告されたように、Ti 3 の光学コントラスト C 2 T x フレークはフレークの厚さに強く依存し、厚いフレークは常に高いコントラストを示し、薄いフレークは低いコントラストを示します[25]。図1bのほとんどのフレークの薄緑色のコントラストは、それらの薄い厚さを示しています。剥離したTi 3 の原子間力顕微鏡(AFM)トポグラフィー画像 C 2 T x フレークを図1bに示します。マッピング領域のフレークは、Ti 3 で一般的な粗さの高い表面を示しています。 C 2 T x フレーク[26]。典型的な薄いフレークの厚さは、図1bのマークされた位置を横切るラインプロファイル(図1bの挿入図)から170nmであると判断できます。剥離したフレークの走査型電子顕微鏡(SEM)画像を図1cに示します。 Ti 3 の積層構造 C 2 T x はっきりと見ることができ、Ti 3 の準備が成功したことを示しています C 2 T x 階層化されたサンプル[10]。
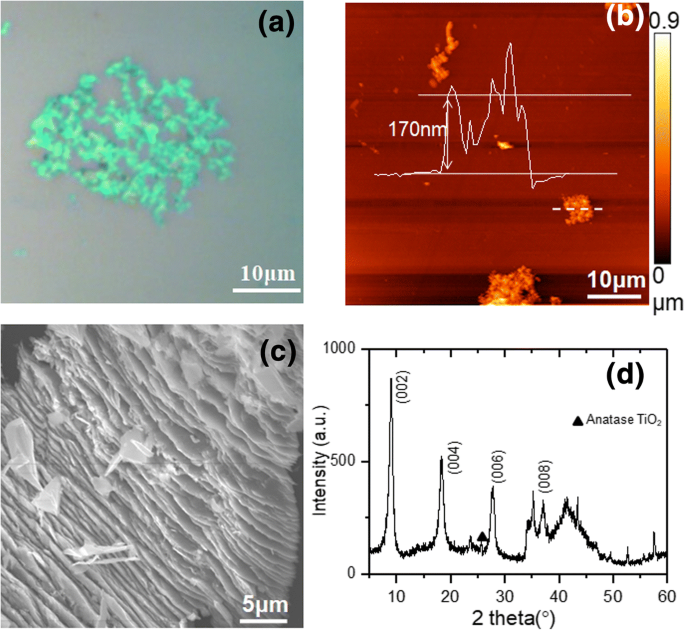
a 超音波剥離したTi 3 の光学画像 C 2 T x フレーク; b 超音波剥離したTi 3 のAFMトポグラフィー画像 C 2 T x フレーク、およびマークされた破線を横切るラインプロファイルは、挿入図として示され、Ti 3 を示します。 C 2 T x フレークの厚さは170nmです。 c 超音波剥離したTi 3 のSEM画像 C 2 T x フレーク; d Ti 3 のXRDスペクトル C 2 T x 生の粉末
さらに、生のTi 3 のXRDスペクトルを測定しました。 C 2 T x 図1dに示すように、粉末。このXRDパターンは、以前のレポート[10]に類似しています。したがって、8.95°、18.28°、および27.7°の顕著なピークは、(002)、(004)、および(006)面の回折に割り当てることができます。顕著なピークと比較して、マイナーフェーズ(アナターゼTiO 2 )の回折ピークの強度 (101)25.3°では、JCPDSカード番号71-1116)は比較的弱く、Ti 3 の純度が高いことを示しています。 C 2 T x 得られた粉末の相。 (002)ピークは、Han etalによって報告された角度よりもわずかに低い角度で現れます。 (9.21°)[10]。計算された c 格子定数19.66Åは、報告された値(19.2Å)よりも大きくなっています[10]。層間空間は、–F、–OH、Li + など、さまざまな密度の化学基とイオンによって調整される可能性があることに注意してください。 、 c 格子定数は、さまざまな研究で19.2Åから58.8Åまで大幅に異なります[10、20、26、27]。 c サンプルの格子定数は、Ti 3 で測定された低い値に非常に近いです。 C 2 T x エッチャントとしてHFを使用するだけの粉末[10]。
Ti 3 のXRDスペクトル C 2 T x 26.7GPaまでさまざまな圧力で測定されたフレークを図2aに示します。異なる圧力で測定されたスペクトルは互いに類似していますが、新しい回折ピークは見つかりません。この結果は、26.7GPaまでの圧力では相転移が発生しないことを示しています。図2aでは、圧力の増加に伴ってすべての回折ピークが大きな角度にシフトし、Ti 3 の収縮を示しています。 C 2 T x 格子。このような疑似負の圧縮率は、Ti 3 でも観察されています。 C 2 T x [20]や、グラファイト[28]、酸化グラフェン[29、30]、MoS 2 など、層状構造を持つその他の低次元材料 [31]、粘土[32]、およびチタン酸塩[33]。 (002)ピークは、圧力が1.8GPaから26.7GPaに増加すると、2.883°から3.162°にシフトします。格子定数の変形率 c 、 c / c 0 、圧力の関数として、(002)ピークのシフトから計算できます。また、 a の変形率 、 a / a 0 、(110)ピークのシフトから計算できます。図2bに示すように、格子定数 c および a 26.7 GPaの圧力で、それぞれ9.1%と2.4%変形します。 〜3 GPaの低圧領域では、格子定数の圧縮比 c 3%です。以前のTi 3 の高圧XRD測定では C 2 T x フレーク、少し大きい c 乾燥Ti 3 の圧縮率4% C 2 T x フレークはGhidiuらによって報告されました。 [11](図2b)。この違いは、より大きな格子定数 c によって引き起こされる可能性があります。 (25.1Å)Ghidiuらが使用したサンプル。 [11]私たちのもの(19.66Å)に関して。
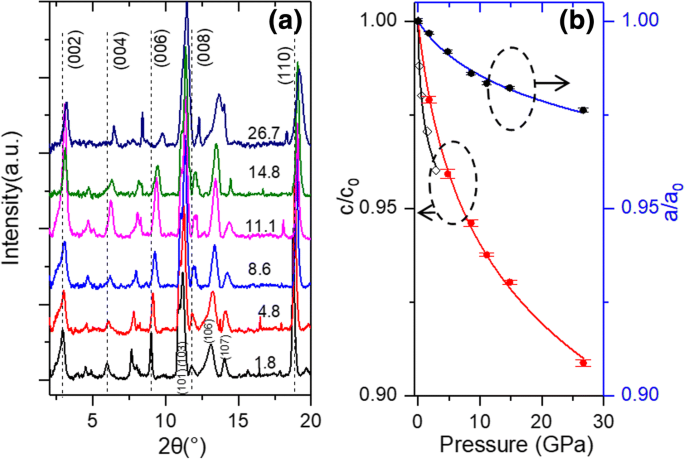
a Ti 3 のXRDスペクトル C 2 T x 異なる負荷圧力で。単位は、各スペクトルに注釈が付けられた圧力のGPaであることに注意してください。ピークは参考文献に従って割り当てられます。 [26]; b c に沿った実験(点)および計算された圧縮率(実線) および a 方向。実線は、方程式\(r(P)/ {r} _0 ={\ left [\ left({\ delta} _0 / {\ delta} ^ {\ prime} \ right)P +1を使用した近似結果です。 \ right]} ^ {\ delta ^ {\ prime}} \)
弾性定数を取得するには、 c および a 図2bの圧縮比は、Murnaghanの式[34]を使用してさらに適合されます。
$$ r(P)/ {r} _0 ={\ left [\ left({\ beta} ^ {\ prime} / {\ beta} _0 \ right)P + 1 \ right]} ^ {-1 / { \ beta} ^ {\ prime}} $$(1)ここで r c に沿った格子定数を表します および a 軸、\({\ beta} _0 ^ {-1} =-{\ left(\ frac {dlnr} {lnP} \ right)} _ {P =0} \)は線形圧縮率、β ' βの圧力導関数です 。
取り付けられた r / r 0 a の曲線 および c 図2bに実線でプロットされています。実験結果は方程式の期待に非常によく適合していることがわかります。最適なフィッティングはβを生成します 0 およびβ ' c の場合 それぞれ67.7GPaと25.5として。一方、格子定数 a 、β 0 およびβ ' それぞれ387.4GPaと72.1と計算されます(表1)。グラフェンなどの極薄2D材料の場合、ヤング率(1TPa)はβに非常に近くなります。 0 厚いグラファイトの[19、28]。したがって、β 0 Ti 3 の弾性定数を評価するための代替として使用できます C 2 T x 。 Ti 3 のヤング率 C 2 T x 最近、Lipatovらによって測定されました。 330 GPa [18]であり、これはβと一致しています。 0 私たちの研究では。測定値は、Ti 3 の弾性定数にも匹敵します。 C 2 他の研究で計算されたものです[15、17](表1)。 β 0 c で 軸がグラファイトの軸よりも大きい(β 0 = 35.7 GPa)、β 0 a で 軸はグラファイトの軸よりも小さい(β 0 = 1250 GPa)[28]。 β 0 Ti 3 の C 2 T x MoS 2 の体積弾性率よりも高い (270 Pa)[35]であり、酸化グラフェン(210 GPa)[36]にも匹敵し、Ti 3 の高い弾性定数を示しています。 C 2 T x 2Dマテリアルの中のMxene。
<図>Ti 3 の高圧ラマンスペクトル C 2 T x 図3aに示すように、サンプルは25.5GPaまでのさまざまな圧縮圧力で測定されました。さまざまな減圧圧力で得られたラマンスペクトルを図3bに示します。低圧縮圧力では、Ti 3 C 2 T x Mxeneは、〜210、〜500、700 cm -1 に3つの主要なラマンバンドを示します。 。 Ti 3 のラマンスペクトルに注意する必要があります C 2 T x MXeneは、さまざまな種類の文献で大きく異なります。 Hu etal。 [23]は〜200 cm -1 に強いラマンピークを報告しました および720cm -1 、400 cm -1 の他のバンド かなり広かった。しかし、ハン等。 [10]およびZhuetal。 [37]は〜200 cm -1 で鋭いピークを観察しました 、しかし他のバンドはすべて広かった。 Xue etal。 [14] 100〜700 cm -1 の広いピークのみが観察されました 。図3のラマンスペクトルは、参考文献のラマンスペクトルとは異なります。 [10、14、23、37]。この違いは、Ti 3 上の化学基の種類と濃度が異なることによって引き起こされる可能性があります。 C 2 T x MXene。これらの異なるラマンバンドをさらに解釈するには、Ti 3 のフォノン分散を思い出す必要があります。 C 2 T x それはHuらによって理論的に計算されました。 [23、24]。 Ti 3 の空間群 C 2 T x P6 3 でした / mmc [23]。原子の数( N )Ti 3 の原始セル内 C 2 T x x が与えられた場合、T =-O、-F、および-OHに対してそれぞれ7、7、および9と計算されました。 =2. Γで 最初のブリルアンゾーンのポイントでは、次の光学フォノンがさまざまなTi 3 に存在すると予測されます。 C 2 T x MXenes:Γ <サブ>オプティカル (Ti 3 C 2 O 2 )=6 E g + 3 A 1g 、Γ <サブ>オプティカル (Ti 3 C 2 F 2 、Ti 3 C 2 (OH) 2 )=8 E g + 4 A 1g [23]。 Ti 3 のさまざまなラマン活性モードの原子振動 C 2 F 2 およびTi 3 C 2 (OH) 2 表2に概略を示します。それらの周波数は、Huらによって理論的に計算されました。 [23]であり、表2にリストされています。Ti 3 の場合 C 2 (OH) 2 、4つの面外モードがあります( A 1g :218、514、684、および3734 cm -1 )および4つの面内モード( E g :138、278、437、および622 cm -1 )。 Ti 3 の場合 C 2 F 2 、3つの A があります 1g モード(190、465、694 cm − 1 )と3つの E g モード(128、231、および612 cm − 1 )[23]。
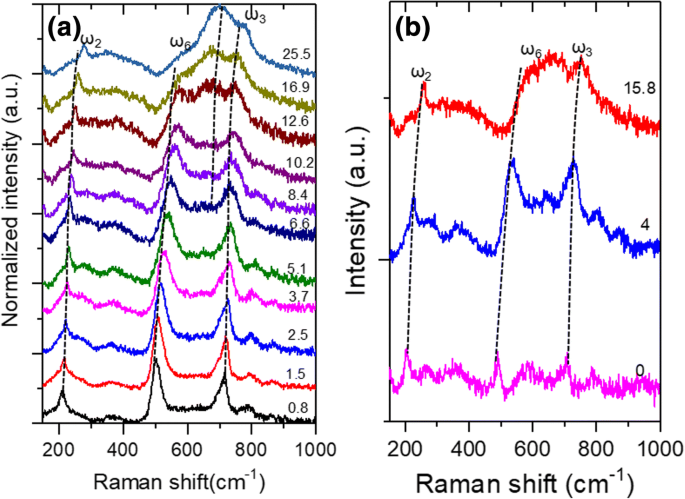
a Ti 3 のラマンスペクトル C 2 T x 異なる圧縮圧力でのフレーク; b 異なる減圧圧力で得られたラマンスペクトル。 a の圧力の単位に注意してください および b GPaです
ただし、純粋なTi 3 の計算されたフォノン周波数を見ることができます。 C 2 F 2 またはTi 3 C 2 (OH) 2 Ti 3 の実験的なラマンスペクトルに適合できません C 2 T x 図3の場合。Ti 3 の表面が C 2 T x 通常、は異なるタイプの化学基によって結合されます。図3の実験的なラマンスペクトルを完全に解釈するには、-Fと-OHの混成振動モードを考慮する必要があります[23]。以前の研究[23]では、〜200、〜500、および〜700 cm -1 のラマンバンド ω 2 に割り当てられました 、ω 6 、およびω 3 、 それぞれ。この指示に従って、205.6、490.2、および702.5 cm -1 の顕著なラマンバンド 図3aの場合、bはω 2 に割り当てることができます。 、ω 6 、およびω 3 それぞれモード。興味深いことに、これらのモードはすべて面外モードです。他のラマンモードは、強度が低いため、隣接するモードから分離するのが困難です。不確実性を排除して堅牢なデータを取得するために、以下の計算と分析ではこれら3つのモードのみが考慮されます。
図3a、bでは、これらの面内モードの相対強度が圧縮圧力の増加とともに増加することもわかります(図3a)。圧縮圧力が≥12.6GPaの場合、〜600 cm -1 に新しいピークがあります。 (ω 4 )出現し、顕著なピークになります。減圧プロセスでは、このω 4 の強度 モードが大幅に減少します。減圧圧力0GPaで得られたラマンスペクトルには、ほぼすべての面内および面外フォノンモードが含まれています。高圧縮圧力での面内モードのこのような出現は、フレーク破壊または配向回転によって誘発される分極に関連している可能性があります。この効果に関する研究はまだ進行中であり、将来報告される予定です。
圧力を0.8GPaから25.6GPaに上げると、ω 2 、ω 6 、およびω 3 すべてが単調に増加するブルーシフトを示し(図4a〜d)、これはグラファイト[28]およびMoS 2 の圧力依存のブルーシフトに類似しています。 [31]。 25.6 GPaでは、これら3つのモードのブルーシフトは66.7、85.1、および60 cm -1 です。 、 それぞれ。このような圧力依存のブルーシフトは、MoS 2 のブルーシフトよりもはるかに大きくなります。 [31]。ラマンシフトと圧力を定量化するために、図4a、b、dのラマンシフトプロットを次の式[28]を使用してフィッティングしました。
$$ \ omega(P)/ {\ omega} _0 ={\ left [\ left({\ delta} _0 / {\ delta} ^ {\ prime} \ right)P + 1 \ right]} ^ {\ delta ^ {\ prime}} $$(2)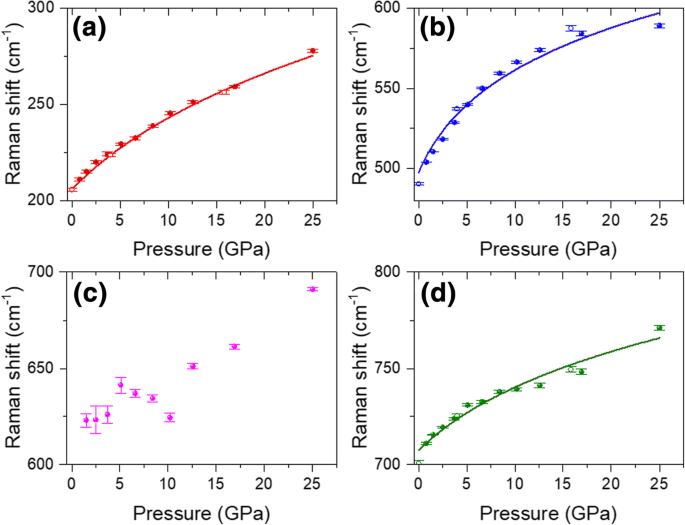
さまざまな圧縮圧力(黒丸)と減圧圧力(白丸)の関数としてのさまざまなフォノンモードのラマンシフト: a 210 cm -1 、 b 504 cm -1 、 c 620 cm -1 、および d 711 cm -1 。実線は、方程式\(\ omega(P)/ {\ omega} _0 ={\ left [\ left({\ delta} _0 / {\ delta} ^ {\ prime} \ right)P +を使用したフィッティング結果です。 1 \ right]} ^ {\ delta ^ {\ prime}} \)
ここで、δ 0 およびδ ' は対数圧力導関数(dlnω / dP ) P =0 およびdlnωの圧力導関数 / dP 、 それぞれ。当てはめた結果は、図4a、b、dに実線でプロットされています。低圧領域では不確実性が高いため、620 cm -1 のラマンモード 取り付けられていませんでした。図4a、b、dから、フィッティング曲線が実験結果と一致していることがわかります。これは、フィッティングプロセスの精度が高いことを示しています。得られたδのパラメータ 0 およびδ ' 表3にリストされています。
<図>MXeneやグラフェンなどの原子の厚さを持つ異方性2D材料の場合、グリュナイゼンテンソルの2つの独立した成分は、通常、 c に平行および垂直なひずみに関連付けられます。 軸。簡単にするために、Zallenらによって提案されたスケーリング関係を採用しました。 [38]、これは、Hanfland etal。によってグラファイトの圧力依存ラマンシフトを適合させるために使用されています。 [28]
$$ \ omega(P)/ {\ omega} _0 ={\ left [r(P)/ {r} _0 \ right]} ^ {3 \ gamma} $$(3)ここで r は、それぞれ層内モードと層間モードの面内および面外の格子定数を指します。 γ 他の研究で定義されたグリュナイゼンパラメータと同等です[39、40]。
圧縮プロセスでは面外モードのみが観察されるため、 c 静圧の関数としての格子定数は、計算に適しています。グリュナイゼンパラメータγの計算には、図2bの(002)平面の0〜26.7GPaの空間距離データを採用しました。 。 ω 2 の平均\(\ overline {\ upgamma} \)最大26.7 GPa 、ω 6 、およびω 3 それぞれ1.08、1.16、0.29と計算されました(表2)。グラファイトと同様に、ω 3 の小さい方の\(\ overline {\ upgamma} \) 他の2つのモードと比較して、力の定数の小さな変化が剛体層の運動に関与していることを示しています[28]。私たちの知る限り、Ti 3 のグリュナイゼンパラメーター C 2 T x まだ報告されていません。ただし、データを他の2Dマテリアルと比較することはできます。 Zha etal。 Ti 2 の音響フォノンモードのグリュナイゼンパラメータを4〜5と報告 CO 2 [41]。高周波光学モードのグリュナイゼンパラメータは通常、低周波モードのグリュナイゼンパラメータよりも1〜2桁低いため[28]、Ti 2 の光学フォノンのグリュナイゼンパラメータは CO 2 0.05〜0.5と見積もることができます。これは、Ti 3 の値と同様です。 C 2 T x 。最近、Peng etal。 [42]は、MoS 2 の室温でのグリュナイゼンパラメーターを1.22、1.20、および1.15と報告しました。 、MoSe 2 、およびWS 2 それぞれ、私たちの結果よりも大きいです。また、結果はグラフェンの結果よりも小さくなっています( E の場合は1.99) 2g モード)[40]およびグラファイト( E の場合は1.06 2g モード)[28]。この発見は、Ti 3 C 2 T x MXeneは、これらの極薄2D材料の中で最も弱い結合非調和性を持っています[42]。
結論
結論として、Ti 3 の格子変形とフォノン応答を測定しました。 C 2 T x 最大26.7GPaのさまざまな静水圧での薄いフレーク。 26.7 GPaの圧力以下では、相変態は観察されていません。すべてのフォノンモードは、圧力の増加に伴って正の周波数シフトを示します。 3つの面外フォノンの正のグリュナイゼンパラメーターは、1.08、1.16、および0.29と計算されます。私たちの結果は、Ti 3 の機械的および熱的特性の理解を深めます C 2 T x 高圧で。
メソッド
Ti 3 C 2 T x 参考文献[43]で報告されている方法で粉末を調製した。簡単に言うと、Ti 3 AlC 2 粉末(Forsman、10 g)をHF溶液(160 ml)で、室温で5時間エッチングしました。得られたTi 3 C 2 T x 粉末を脱イオン水に分散させ、700 Wの電力で超音波剥離しました。得られた溶液は、24時間保管した後に分離しました。得られた上層溶液は、さらなるラマン、原子間力顕微鏡(AFM)、および走査型電子顕微鏡(SEM)分析に使用されました。周囲圧力でのX線回折(XRD)スペクトルは、X線回折計(Rigaku、MiniFlex600)を使用して測定しました。 SEM画像は、走査型電子顕微鏡(日立、Su1510)を使用して得られた。その場高圧XRD測定は、上海シンクロトロン放射施設で、室温でガスケット高圧ダイヤモンドアンビルセル(DAC)によって実行されました。サンプルの周囲に静水圧環境を作り出すために、圧力伝達媒体としてメタノール/エタノール/水(16:3:1)を使用しました。圧力は、鋭いルビー蛍光R1線の圧力依存スペクトルシフトによって決定されました。サンプルは、ダイヤモンドキューレット(直径400μm)が付いたステンレス鋼のガスケット穴(直径100μm)に配置されました。高圧ラマン散乱測定は、励起波長532nmのレニショーinViaラマン分光計を使用して実行されました。地形測定はAFM装置(Bruker、Innova)で実施されました。
回折ピーク位置とラマンピークシフトのフィッティングは、OriginProパッケージで実行されました。ユーザー定義関数、 y =(A1× x + 1) A2 、A1とA2をフィッティングパラメータとして設定して使用しました。シンプレックス法で簡単に適切なフィッティングが得られます。
略語
- 2D:
-
二次元
- AFM:
-
原子間力顕微鏡
- DAC:
-
ダイヤモンドアンビルセル
- SEM:
-
走査型電子顕微鏡
- TMD:
-
遷移金属ジカルコゲニド
- XRD:
-
X線回折
ナノマテリアル
- X線シンクロトロン粉末回折によって調べたHoCo0.5Cr0.5O3の異常な熱膨張
- ボロフェンの安定性とSTM画像に関する第一原理研究
- TIPS-ペンタセンベースの有機電界効果トランジスタの移動度と形態に及ぼすその場アニーリング処理の影響
- 角度分解X線光電子分光法によるAl2O3キャップGaN / AlGaN / GaNヘテロ構造の表面分極に関する調査
- HT29およびSPEV細胞株に対するAuナノ粒子の影響のinvitro研究
- 2〜5nmのサイズ間隔でのナノダイヤモンドのラマンスペクトルと体積弾性率
- らせん状溝管内のTiO2-水ナノ流体の流れと熱伝達特性に関する実験的研究
- Pt / Nd:SrTiO3接合におけるマルチレベル抵抗スイッチングメモリとメモリ状態依存光起電力に関する研究
- 抵抗変化型メモリのモデリングとシミュレーションに関する集合的研究
- 水性電解質中の対称スーパーキャパシタとしてのカーボンナノファイバーと活性炭の研究:比較研究
- 天然および合成ナノ材料の電気化学的、生物医学的、および熱的特性の比較研究



