楕円形のグラフェンと黒色のリンのペアを使用した、調整可能で異方性のデュアルバンドメタマテリアル吸収体

はじめに

グラフェンは、炭素原子がハニカム格子に配置された2次元材料です[1、2]。さまざまなグラフェンベースのフォトニックデバイスが、その超小型サイズと独自の光グラフェン相互作用のために、近年開発されてきました[3,4,5,6]。その最も重要な用途の1つとして、グラフェンに基づくメタマテリアル吸収体は、その強力で調整可能なプラズモン応答により、急成長する関心を集めています[7、8、9、10]。ただし、グラフェンのバンドギャップがゼロまたはゼロに近いため、高いオンオフ比を必要とするいくつかのアプリケーションは制限されています[11]。代替の二次元材料として、しわの寄った構造を持つ六角形の格子に配置されたリン原子の単分子層である黒リン（BP）[12]も、最近研究の関心が高まっています。面内異方性、厚さに依存する調整可能なバンドギャップ[13]、高いキャリア密度と移動度[14]など、優れた光学的および電子的特性を備えています。過去数年にわたって、赤外線領域で、研究者はBPに基づくメタマテリアルの光-BP相互作用強度を強化するために多くの構造を調査してきました[15、16、17]。それにもかかわらず、BPベースの吸収体のプラズモン共鳴は、柔軟かつ効果的に調整することはほとんどなく、通常、適度なドーピングレベルで比較的低い吸収率に悩まされます。これは、単分子層BPの共鳴強度がかなり弱く、異方性電位が制限されているためです。したがって、グラフェンとBPの混成を利用して、強力で異方性のプラズモン吸収を実現する、グラフェン-BPベースのプラズモン吸収体が提案されています[18、19、20]。ただし、以前に報告されたグラフェン-BPベースの吸収体は、一般に比較的複雑な製造技術を必要とするか、単一の吸収帯を持っているため、イメージング、バイオセンシング、および通信システムへのさらなる応用が妨げられます。

私たちの仕事では、異方性デュアルバンド赤外線吸収体は、製造が容易な周期的な楕円グラフェン-BPペアを使用して数値的に提案されています。幾何学的サイズとドーピングレベルによる共鳴の独立した調整可能性が実証されています。電界分布をプロットして、物理的なメカニズムを明らかにします。入射角の許容誤差と偏光感度も示されています。

メソッド

提案された吸収体は、SiO ₂ 上に堆積された横方向および縦方向の楕円形グラフェン-BPペアで構成されています。 図1に示すような層。六方晶窒化ホウ素（hBN）層は、単分子層グラフェンとBPの間に絶縁スペーサーとして挿入され、それらの間のキャリア輸送を防ぎ、高いキャリア移動度を保証します。 SiO ₂ のパラメータ およびhBNは参考文献から取得されます。 21およびRef。それぞれ22。シミュレーションはCOMSOLMultiphysicsによって実行され、周波​​数領域での有限要素法（FEM）に基づくデュアルバンド特性を調査します。両方の x の境界条件として、フロケ周期性を適用します。 -および y - 方向。計算領域の上面には赤外波励起のポートが設定され、下面には完全電気導体（PEC）境界条件が設定されています。ユーザーコントローラーメッシュ密度の四面体メッシュがドメイン全体に適用されます。

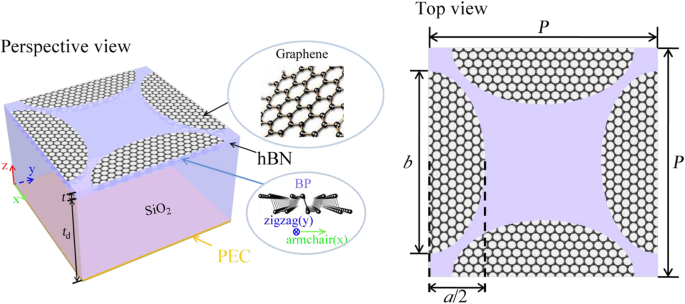
楕円形のグラフェン-BPペアに基づく提案された吸収体のユニットセル。 t _d とtは、それぞれ誘電体層と絶縁体層の厚さです。 a および b 楕円の短軸と長軸です。 P は正方形のユニットセルの周期的な辺の長さです

シミュレーションでは、グラフェンとBPの両方が、誘電率テンソルを備えたバルク材料ではなく、表面導電率を備えた2次元表面として扱われます。この仮定は、極薄材料の厚さ定義と低い計算効率の問題を解決します[23]。

グラフェンの表面抵抗率を説明するにはσ （ω ）、以下のようによく知られている久保公式を使用します[24]：

式によると。 1、σ （ω ）は、バンド内およびバンド間の対応物、つまりσで構成されます。 _イントラ およびσ _inter 。 ω はラジアン周波数、μ _c は化学ポテンシャルです、Г は散乱率であり、 T ケルビン温度です。 ħ 、 e 、ξ 、および k _B は、それぞれ、減少したプランク定数、電子電荷、電子エネルギー、およびボルツマン定数です。

赤外領域では、入射光子はバンド間遷移をほとんど励起できないため、光-グラフェン相互作用はバンド内遷移によって支配されます。特に、μ _c の場合 ≫ k _B T 、久保公式はさらに式（1）に簡略化できます。 5：

したがって、グラフェンの表面抵抗率は、ωの値に依存します。 、Г 、およびμ _c 。ここで、Г 0.3meVおよびμと想定されます _c 前の研究[25、26]によれば、0.7eVであると想定されています。

一方、表面抵抗率σを計算します。 _j 単純な半古典的ドルーデモデルによるBPの比較[27]：

ここで n _s は、ドーピングレベルに関連するキャリア密度です。 n を選択します _s =1.9×10 ¹³ cm ⁻² およびГ _BP = 以前の参考文献[16]によると10meV。 j が関係する方向なので、σ _x およびσ _y x に沿った電子質量によって決定されます -および y -それぞれ方向。 m _x および m _y さらに次のように計算できます：

ここで m ₀ は標準の電子質量であり、Δ および a はそれぞれBP単分子層のバンドギャップとスケール長です。式を代入することによって。 10–12を式に代入します。 8と式。 9、アームチェアに沿った電子質量を取得できます（ x -）およびジグザグ（ y -） 方向。それらの間の不一致は、BPの異方性表面伝導率に寄与します。

結果と考察

提案された吸収体の異方性吸収特性を説明するために、最初に吸収スペクトルをシミュレートして、個々のグラフェン層、個々のBP層、およびグラフェン-BPペアと比較します。図2aで観察できるように、グラフェンのプラズモン応答は等方性であり、分極に関係なく、9.9μmと15.4μmに2つの明らかな吸収ピークがあります。一方、BPのプラズモン共鳴は異方性ですが、TE（<12.7％）またはTM（<0.7％）のいずれの発生率でもその強度は非常に弱いです。グラフェンとBPの利点を組み合わせることにより、グラフェンとBPのペアは強いプラズモン応答と異方性プラズモン応答の両方を示します。 TE発生率の場合、2つの吸収ピークは8.8μmと14.1μmにあり、吸収率は90％を超えています。 TM入射の場合、最大吸収の波長はそれぞれ9.5μmと15.4μmにシフトします。偏光消光比は、PER =10×log（ R ）として定義できます。 ₁ / R ₀ ）、ここで R ₁ および R ₀ 反射率を示します（ R =1- A 、 A 同じ波長での異なる偏光の吸光度を表します。各共振の最大PERは、λで最大23dBおよび25dBに達する可能性があります。 =9.5μmおよびλ =14.1μm、それぞれ。したがって、提案された吸収体は、高性能のデュアルバンド反射偏光子として利用することができます。

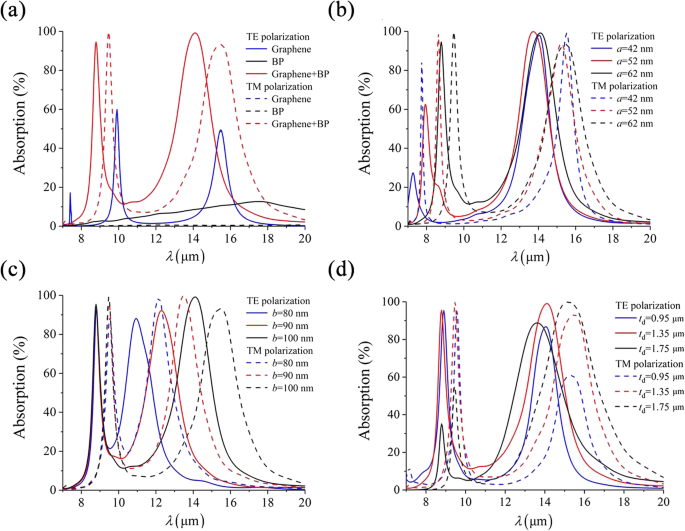
a 単層グラフェン（青い実線の曲線と青い破線の曲線が重なっている）、単層BPとグラフェン-BPのペア、および異なる a の吸収スペクトル間のプラズモニック応答の比較 （ b ）、 b （ c ）、および t _d （ d ）。デフォルトのパラメータは a です =62 nm、 b =100 nm、 t _d =1.35μm、 t =5 nm、および P =250 nm、法線入射下

次に、さまざまな幾何学的構成の吸収スペクトルを分析して、図2b–dの調整可能なデュアルバンド吸収特性を示します。図2bでは、最初の吸収ピークは a のように赤方偏移しています。 両方の偏波で42nmから52nmに増加しますが、2番目の共振周波数はほとんど変化しません。一方、図2cに示すように、長軸の長さを長くすることにより b 、2番目の共鳴も赤方偏移しますが、最初の吸収ピークはTEおよびTM偏光に対して一定のままです。したがって、楕円グラフェンとBPのペアで対応する軸の長さを変えることにより、二重吸収ピークを個別に調整できます。さらに、誘電体層の厚さも、提案されたデバイスの性能に重要な役割を果たします。これは、グラフェン-BPメタ表面とPEC基板によって形成されるファブリペロー共振器として機能します。したがって、異なる t の吸収スペクトル _d 図2dにプロットされています。 t として _d 0.95から1.75μmに増加すると、TEおよびTM偏光の最初の吸収ピークは劇的に低下しますが、2番目のピークは最初に増加してから急激に減少します。結果として、最適な厚さがあります t _d 提案された吸収体の二重吸収ピークを最大化します。

物理的な洞察を解明するために、図3でさまざまな波長での電界強度分布をさらに明らかにします。TE入射の場合、電界はアームチェア（ x ）にあります。 -） 方向。最初のピーク（λ =8.8μm）、入射赤外光はグラフェンとBPの電子を励起して横方向に振動させ、図3aに示すように縦楕円の短軸端に電界を集中させることができます。 λで =14.1μm、局所的な電界は、横楕円の長軸端で増強されます。一方、ジグザグ（ y ）の電界によるTM入射 -）方向は、電子を励起して9.5μmの吸収ピークで縦方向に沿って振動させ、横楕円の短軸端に集中した電界分布をもたらします。その上、λで =15.4μm、電界の増強は、縦楕円の長軸端に集中します。したがって、共鳴波長は、横方向と縦方向の両方の楕円形グラフェンとBPペアで誘導された双極子の有限振動長に直接関係しています。

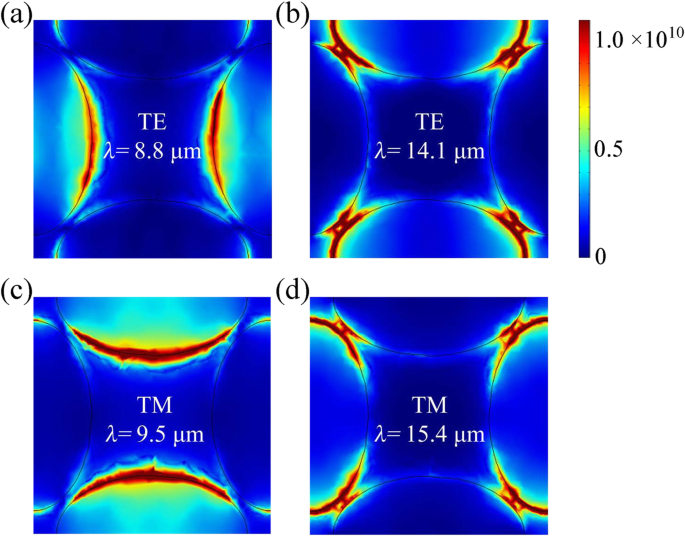
a のさまざまな波長での電界強度分布 、 b TEおよび c 、 d TM分極、ここで a =62 nm、 b =100 nm、 t _d =1.35μm、 t =5 nm、 P =250 nm、法線入射下

図2b–dに示すように、幾何学的寸法を変えることにより、異方性デュアルバンド吸収性能を効果的に調整できます。一方、グラフェンとBPの表面導電率は、μ _c を変化させることによって操作することもできます。 および n _s 上記のグラフェンおよびBPモデル式による。 μ _c および n _s 幾何学的製造後に変更できるグラフェンとBPのドーピングレベルを表します。したがって、異なるμで提案された吸収体の性能 _c および n _s 図4に示します。実際の状況を考慮して、μ _c 実験によって検証された以前の研究から0.4から0.8eVの間で選択されます[28]。以前に報告された研究[29]では、 n の最大理論値 _s BPのは2.6×10 ¹⁴ であることが実証されました cm ⁻² 、中程度の n _s 10 ¹³ から選択されます cm ⁻² および10 ¹⁴ cm ⁻² シミュレーションで。図4aでは、μの場合 _c =0.4 eV、最初の吸収ピークは10.9μmにあり、2番目の吸収ピークは17.1μmにあります。 μとして _c 0.8 eVに増加すると、2つの共振波長は8.4μmと13.4μmにブルーシフトされます。同様に、TM偏光の場合、二重吸収ピークは、μでそれぞれ12.4および19.8μmから8.9および14.4μmにブルーシフトされます。 _c 図4bに示すように、0.4から0.8eVに増加します。個々のパターン化されたBPの場合、共鳴波長λ _p \（{\ lambda} _p \ propto \ sqrt {L / {n} _s} \）として計算できます。ここで、 L は実効発振長です[27]。したがって、 L が固定されている場合、吸収スペクトルは n として明らかな青方偏移を示します _s 図4cにプロットされているように、TE分極の増加。 TM偏光の場合、吸収ピークも n としてわずかにブルーシフトされます。 _s 10 ¹³ から増加 cm ⁻² 〜10 ¹⁴ cm ⁻² 図4dに示すように。

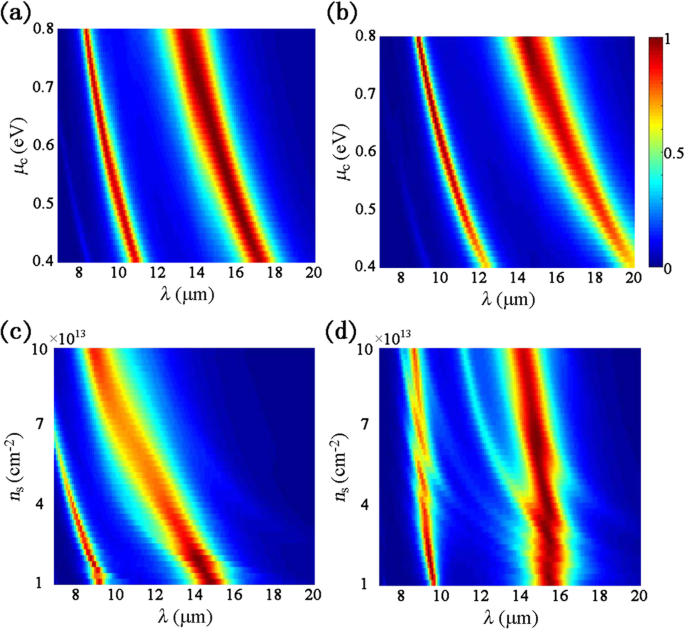
法線入射下での吸収スペクトルとさまざまなドーピングレベルの比較： a および b グラフェンのさまざまな化学ポテンシャルの場合、 c および d BPのさまざまなキャリア密度の場合、 a および c TE偏光の場合、および b および d TM偏波の場合、 a =62 nm、 b =100 nm、 t _d =1.35μm、 t =5 nm、および P =250 nm

実際のアプリケーションでは、赤外線吸収体には広い入射角の許容誤差が好まれます。したがって、斜め入射下での吸収スペクトルを詳しく説明します。図5aでは、TE分極の場合、θのときに最初の吸収ピークが80％より大きいままであることが観察されます。 θの場合でも、2番目の吸収ピークは80％を超えて維持されますが、52°に増加します。 80°に増加します。 θの場合> 46°、2番目の共鳴波長はθとして徐々に赤方偏移します 大きくなります。 TM発生率の場合、θの場合 が62°未満の場合、最初のピークでの吸収率は90％を超えて維持されますが、共振波長はλで一定に保たれます。 図5bに示すように=9.5μm。さらに、2番目の共鳴では、θでピーク吸収が80％を超えたままになります。 60°まで、その後θの増加とともにわずかに低下します 。優れた角度安定性は、斜めの入射角に対してロバストなファブリペロー共振器の共通の特徴に由来します[30]。

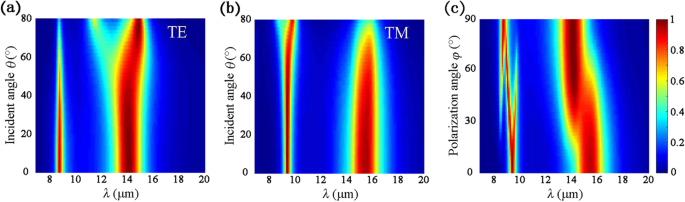
a のさまざまな入射角での吸収スペクトル TEと b TM偏光と c 法線入射下でのさまざまな偏光角。幾何学的パラメータは図4と同じです

異なる偏光角での垂直入射下での吸収スペクトルφ 提案された吸収体の偏光依存性を調査するために図5cに示されています。 TE偏光の偏光角を0°と仮定します。図5cから、φとしてわかります。 0から90°に増加すると、吸収スペクトルは図2aのTM偏光と同じであることがわかります。 0°<φの場合 <90°、入射はBPの電子を励起し、その x により、アームチェアとジグザグの両方向に振動します。 -および y -入射電界の成分。その結果、表面プラズモン共鳴は、BPのアームチェアとジグザグ方向に同時に誘導される可能性があります。

結論

結論として、周期的な横方向および縦方向のグラフェン-BP楕円からなる異方性デュアルバンド赤外線吸収体を提案しました。各共振での最大PERは、最大23dBおよび25dBに達する可能性があります。二重異方性共振は、短軸と長軸の端にある誘導電気双極子に起因します。短軸と長軸の長さを調整することにより、1番目と2番目の吸収ピークをそれぞれ独立して調整できます。さらに、グラフェンとBPの対応するドーピングレベルを変更することにより、共鳴吸収帯を調整することもできます。さらに、両方のピークでの高い吸収率は、任意の偏光の斜め入射の下で達成できます。提案された吸収体は、調整可能な反射偏光子および新しい赤外線センサーとして利用できます。

データと資料の可用性

すべてのデータは制限なしで完全に利用可能です。

略語

BP：

黒リン

FEM：

有限要素法

hBN：

六方晶窒化ホウ素

PEC：

完全電気導体

TE：

横電気

TM：

横磁気