固体酸化物燃料電池アノードにおける異方性微細構造の進化

背景

固体酸化物形燃料電池（SOFC）は、水素の化学エネルギーを直接電気に変換する電気化学デバイスです。単一のセルは通常、不浸透性で高密度のイオン伝導性電解質が2つの多孔質触媒電極（アノードとカソード）の間に挟まれた平板の形をしています。燃料はアノード側に供給され、空気はカソードに供給されます。非生産的な燃焼を避けるためにガスを混合することはできません。代わりに、ガスは触媒材料に衝突し、電子を失い、電解質の両側にコンデンサを形成します。陰極側では反応が遅いため、2つの電極間に電位差が生じます。この電位差は、酸素圧力勾配とともに、酸素イオンをカソードからアノードに移動させる駆動力です。この点で、電極の微細構造の形態は非常に重要です。典型的なアノードは、ニッケル相（Ni）、イットリア安定化ジルコニア相（YSZ）、および細孔相で構成されます。各材料は、さまざまな種に経路を提供することにより、SOFC全体の輸送プロセスで重要な役割を果たします。アノードの場合、YSZ相は酸素イオンへの経路を提供し、Ni相は電子を提供し、細孔相はガスが電極に浸透することを可能にします。電気化学反応は、3つの相すべてが接触しているライン、いわゆる三重相境界（TPB）でのみ発生します。細胞を横切る輸送現象を図1に模式的に示します[1]。

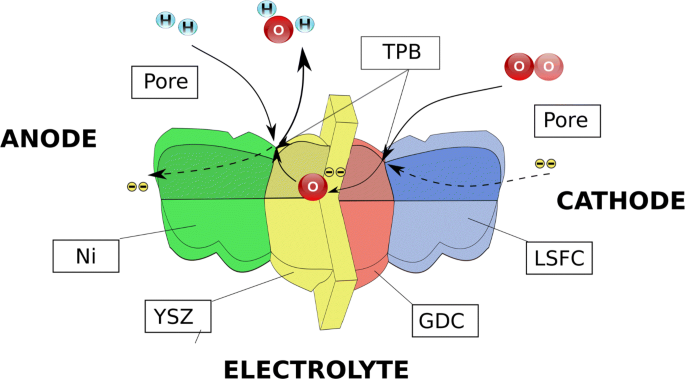
微細構造の役割が強調された、典型的な固体酸化物燃料電池を横切る輸送現象の概略図

アノード複合材料は複雑であるため、微細構造指向の設計はSOFC開発の重要なステップになります[2–7]。この作業では、固体酸化物燃料電池のアノードで長期間の動作中に発生する微細構造の変化を調査します。詳細な分析を提供するために、特定の方向の微細構造の複雑さを反映する異方性の屈曲係数に焦点を当てます。構造解析は、集束イオンビームと組み合わせた走査型電子顕微鏡を使用して行われます。この技術は、2006年にウィルソンらによってSOFCの分野に導入されました。 [8]。この方法では、後続の多くのセクションを直接観察し、その結果を微細構造の3Dデジタル表現に変換できます。再構築された微細構造から、微細構造パラメータを評価することが可能です[9–11]。実際の電極構造から直接得られるこれらのパラメータは、燃料電池システムの長期的な実行中のアノード微細構造の進化を理解するために非常に重要です。この手法は、数値モデリングを改善するために広く使用され[12–17]、最近では、固体酸化物燃料電池のアノードの劣化メカニズムを理解するために使用されました[18–24]。これは、最近の結晶学的研究[25、26]に対する貴重な支持となりました。

この論文では、SOFCスタックの長期運転中の微細構造進化の異方性特性を初めて報告します。微細構造は、主にニッケル粒子の異方性の移動、成長、および粗大化によって進化することを示しています。

実験的な開口部

モジュラースタックテストベンチ

老化試験は、ヨーロッパの大手SOFCメーカーであるSOLID Powerによって設計および開発されたモジュラースタックテストベンチ（MSTB）を使用して実施されました。セットアップの概略図を図2に示します。スタックは電気炉内にあります。

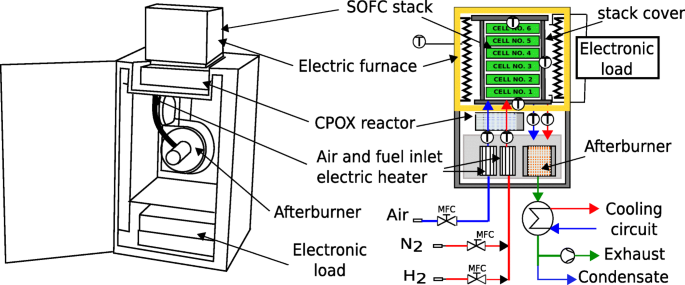
モジュラースタックテストベンチの概略図

燃料と空気は、マスフローコントローラーと予熱器を介してシステムに供給されます。空気と燃料の両方が触媒部分酸化（CPOX）反応器（燃料にメタンが含まれている場合）に供給されるか、燃料が水素と窒素の混合物である場合はそれをバイパスします。予熱後、カソードチャネルに空気が供給されます。供給された空気中の酸素の一部は、電気化学反応で消費されます。同時に、セルスタックから熱を取り除くために空気が使用されます。次に、空気がアフターバーナーに送られ、アノードチャネルからの未使用燃料を燃焼させます。空気処理の反対側では、燃料が酸化されて発電します。この研究で水素の混合物であった燃料（H ₂ ）および窒素（N ₂ ）予熱後、アノードチャネルに供給されます。残留燃料はアフターバーナーで酸化されます。燃焼プロセスの後、ガスは冷却され、凝縮水が分離され、乾燥ガスは最終的に周囲の空気に排出されます。

図2で「T」とマークされた7つの熱電対は、温度分布を監視します。各バイポーラプレートはワイヤーに接続され、ワイヤーはポテンシオスタットに接続されます。この構成により、スタック内のすべてのセルの電流-電圧特性を取得できます。セルの寸法は60×80 [mm×mm]です。反応に利用できるアクティブセルの面積は48 [cm ² ]。セルは最大75％の燃料利用率を実現し、1 [W cm ^-2 を超える高出力密度を実現できます。 ]。スタックは、燃料と空気の流れが同じ方向になる並流構成で構成されています。システムでは、水素と窒素の混合物が燃料として使用されました。

セットアップの詳細については、他の場所で見つけることができます[27、28]。

集束イオンビーム-走査型電子顕微鏡

デュアルビームシステムは、走査型電子顕微鏡（SEM）と集束ガリウムイオンビーム（FIB）の光源を1つのチャンバーに組み合わせたものです。 SEMはイメージングに使用され、FIBは主にフライス盤に使用されます。限られた状況では、FIBを観測に使用できます。システムは、調査されたサンプルの後続のセクションのユニークな可能性を提供します。ホルダーに配置できる材料のサンプルの通常のサイズは25mm ² です。 。 FIB-SEMのセットアップと測定手順を図3に模式的に示します。イオンガンの方向はサンプル表面に垂直であり、電子銃はイオン源に対してある角度で傾けられています。サンプルのセクションの観察。 1回の手順で観察できるサンプルの対象ボリュームは約1000 μです。 m ³ 。集束イオンビームは、トレンチを作成し、最小の代表的なボリュームサイズの要件を満たすサンプルの交差点を露出するために使用されます。トレンチが作成された後、交差点は低エネルギーGa ⁺ を使用して研磨されます ビームと画像はレンズ内検出器を使用して撮影されます。これにより、調査対象の相（Ni、YSZ、および細孔）間で非常に優れたコントラストが得られます。 SEM画像が撮影された後、FIBガンは別の交差点を露出するために粉砕し、材料の別の層が除去されます。 「カットアンドシー」手順は、関心のあるボリュームに応じて200〜300枚の画像が得られるまで繰り返されます。この手順は、セクショニングと呼ばれます。手順は次の手順で要約できます。

1. 1

   関心のあるボリュームに炭素層が堆積します。

   

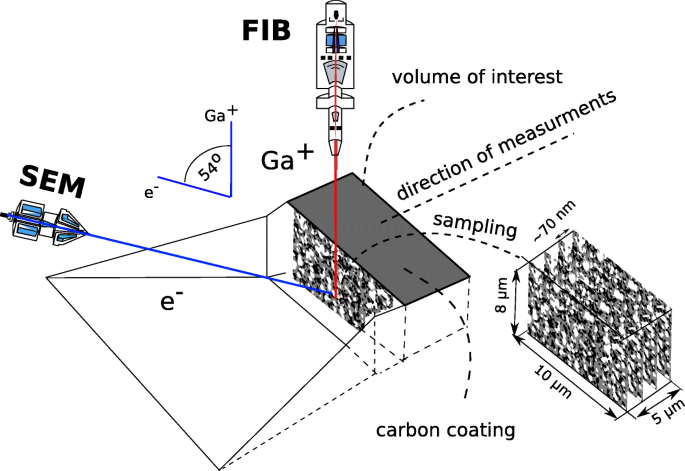
   デュアルビームシステムの構成

2. 2

   サンプルの交差点にアクセスできるようにトレンチが作成されています。

3. 3

   断面は低電流ビームで研磨されています。

4. 4

   観察された交差点のSEM写真は、レンズ内の二次電子検出器を使用して撮影されます。

5. 5

   FIBガンは、Ga +イオンのビームを使用してサンプルに粉砕し、別の交差点を露出させます。

6. 6

   「カットアンドシー」手順を繰り返して、2D画像のシーケンスを取得します。

カットアンドシー手順のアイデアを図3に示します。

実験的方法論

提示された研究は、発電実験と微細構造研究の2つの部分に分けられました。耐久性の研究は、スタックを長期間にわたって一定の負荷の下に保つことによって実施されました。テストの期間を短縮するために、温度を800 ^{o まで上げました。} 実験開始時に90Wの出力電力を供給するために、Cおよび印加電流は19.4Aでした。燃料利用率は75％でした。詳細な実験条件を表1にまとめています。エージングテスト後、スタックを分解し、テスト後の微細構造分析のために9つのサンプルを選択しました。セル番号から3つのサンプルが抽出されました。図4に示すように、1、3、および5（各セルの上流​​、中央、および下流に配置）。追加のセル、いわゆる参照セルは、還元プロセス直後の新しいセルでした。セルはメーカーから提供されたものであり、電気化学的試験には参加していません。したがって、参照セルの微細構造は、エージングテスト前の微細構造を表していると考えるのが妥当です。 FIB-SEM分析用のすべてのサンプルは、5mm×5mmの正方形の形をしており、ダイヤモンドペンを使用してセル（6cm×8cm）から切り取られました。微細構造の研究の前に、すべてのサンプルにエポキシ樹脂を含浸させ、サンドペーパーで研磨しました。含浸は、SEMイメージング中の細孔相の認識にとって重要です。 9つのサンプルすべてがFIB-SEM技術を使用して分析されました。

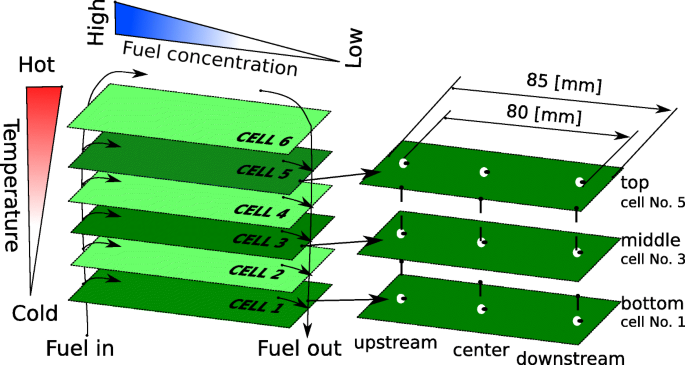
セル内およびスタック内の選択されたサンプルの位置

各サンプルに対して取得されたSEM画像のセットは、画像セグメンテーションプロセスを経て、SEM画像の各領域に3つのフェーズのうちの1つを割り当てました。セグメンテーションは、明るさに基づいて画像領域にラベルを付けるプロセスであり、半自動で実行され、サンプルごとに最大1か月のオペレーター作業が必要です。画像セグメンテーションプロセスに成功した後、画像リサンプリングが行われます（図5を参照）。

画像処理とフェーズラベリングのワークフロー。 a 生の画像。 b 実験的なアーティファクトを手動で削除しました。 c フィルタリング。 d 白はニッケル、黒は細孔、灰色はYSZを表すフェーズラベリング

このホワイトペーパーの後半で紹介するランダムウォークシミュレーションには、キュービックボクセルが必要です。これは、画像間の距離が画像のピクセルサイズと等しくなければならないことを意味します。ただし、スライスが多いほど、セグメンテーションに必要な時間が長くなり、実際には実行不可能です。実際には、画像間の距離は、セグメンテーションの最も時間のかかるプロセス中の時間を節約するために、ピクセルサイズよりも重要です。したがって、セグメンテーションは直方体ボクセルで実行され、後処理中に直方体ボクセルに変換されます。再サンプリングされた画像に基づいて、各相の3次元形態を表す表面は、異なる領域間の界面の三角形近似によって生成されました。三角測量とリサンプリングは、ThermoFisherScientificのAVIZOソフトウェアを使用して実施しました。得られた3次元デジタル素材表現を図6に示します。

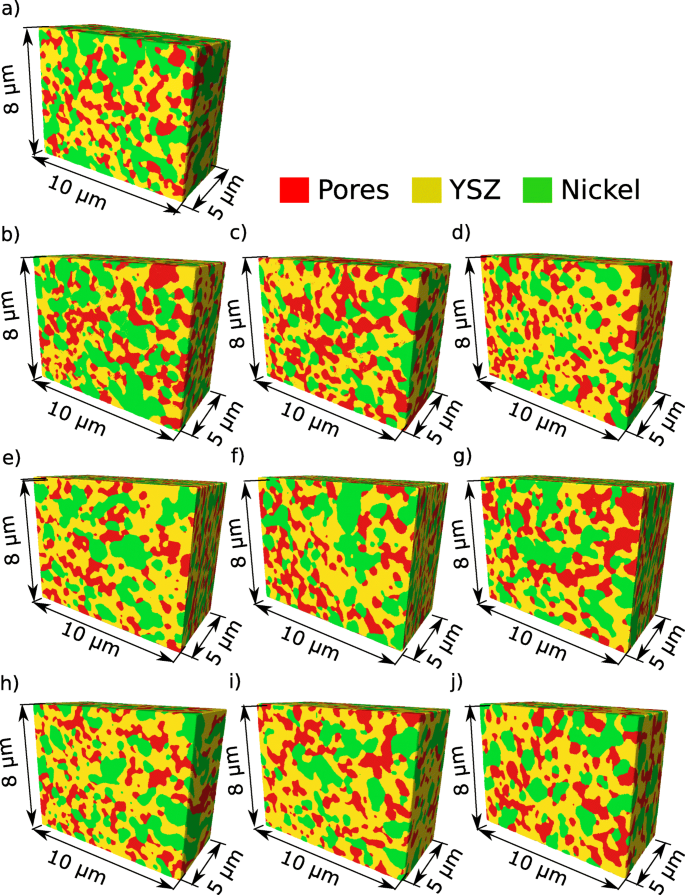
エージングテスト前後のアノード微細構造のデジタル材料表現。 a 参照サンプル。 b セル5の上流。 c セル5の中央 d 。セル5の下流 e セル3の上流。 f セル3の中央 g 。セル3の下流。 h セル1の上流。 i セル1の中央。 j セル1の下流

屈曲係数は、微細構造の複雑さの定量的尺度です。屈曲性の概念は、砂床を通る流れを研究したCarman [29]による多孔質媒体の研究に導入されました。彼は、多孔質媒体内の流体の細長い拡散経路を考慮に入れる要因として、屈曲性を導入しました。彼の研究では、彼は厚さ L の多孔質層を仮定しました _s 均一な断面と長さの曲がりくねった毛細管の束と見なすことができます L _e 。同様に、固体酸化物燃料電池のアノードの場合、屈曲度は実際の拡散経路の長さと電極の厚さの比率として定義できます。この簡略化されたシステムでは、屈曲度は実際の拡散経路の長さの比率 L として定義されます。 _e 、ストレートチャネルの場合のパスへ L _s （陽極の厚さ）：

屈曲度と屈曲度係数の違いを覚えておくことが重要です。カーマンの定式化に照らして、屈曲係数（τ ）は、屈曲度の2乗（τ）として定義されます。 =\（\ bar {\ tau} ^ {2} \））、これは質量拡散方程式の拡張係数として使用されます：

ここで、ε 気孔率、 D _i はガススパイスの拡散係数です i 混合ガスの内部、および D _{i 、eff} は、多孔質媒体内の流体の細長い拡散経路を考慮した有効拡散係数です。

実際のアノードの微細構造では、燃料経路は非常に複雑である可能性があり、ガス接続経路は多くの分岐を作成し、分離し、再結合する可能性があります。したがって、屈曲係数を屈曲度の2乗として表すことはやや象徴的であり、屈曲度と屈曲度係数の実際の関係は、キャピラリーモデルを使用して計算することはできません。一部のグループは、幾何学的な屈曲度を1つの関数に明示的に組み合わせた、いわゆるMファクター、パーコレーションファクター（ P ）を使用してこの問題を克服しています。 ）、収縮係数（β ）、および相体積分率[30]：

ここで a 、 b 、および c 参考文献に記載されている方法論から導出された定数です。 [31]。 Peterson [32]によって導入された収縮係数は、ラッパとボトルネックの比率として理解できます。屈曲係数を推定するための既存のアプローチの包括的なレビューは、Tjaden、Brett、およびShearingによるレビュー[33]にあります。

最近、拡散ベースのアルゴリズムは、収縮係数を必要としないため、ますます注目を集めています。これは、拡散プロセスのシミュレーション中にボトルネックとバルジが直接考慮され、測定値が拡散係数の直接の減少であるためです[34]。

ここで最も有望な方法の1つは、非吸着粒子の屈曲係数を統計的に計算できるランダムウォークプロセスです。この方法では、ランダムウォーカーと呼ばれる多数のマーカーが、図6に赤いボリュームとして示されている細孔フェーズに確率的に分布します。各タイムステップで、各ウォーカーは同じフェーズの隣接するボクセルにランダムに移動します。移行用に選択されたボクセルが別のフェーズに属している場合、ウォーカーは現在の位置に留まり、次のタイムステップを待ちます。このプロセスを繰り返しながら、ランダム歩行者の平均二乗ゆらぎを計算できます。

ここで 𝜗 はランダムウォーク手順の無次元時間であり、 n ランダムウォーカーの数です。

自由空間での格子歩行の平均二乗ゆらぎの正確な解は、[35]：

ここで D ₀ は自由空間での拡散係数[m ² s ^-1 ]、および t [s]の時間です。式からの拡散係数。 （5）導関数を計算することにより、時間の関数として書き直すことができます：

𝜗 時間の関数です t 、式（6）次の形式を取ります：

部分\（\ frac {\ mbox {{d}} \ vartheta} {\ mbox {{d}} t} \）は、式の一部から導出できます。 （5）：

与える

ここで a は、単純な立方格子の格子定数（つまり、FIB-SEMボクセルの寸法）[nm]です。

屈曲係数τ 自由空間と比較した多孔質媒体の平均二乗変位の減少の程度を説明します[34、36]：

式を組み合わせることによって。 （7）と（10）から、次の式が得られます。

これは、さらに式を組み込んだ後です。 （8）と（10）は次のようになります：

移動現象を一方向のみで考える場合、次の式が関係します。

したがって、異方性の屈曲係数を推定するには、式（1）を使用します。 （12）は次のようになります：

この方法は統計に基づいているため、屈曲係数を正しく推定するには、多くの歩行者と大きな平均二乗変位が必要です。最終的に、歩行者は、微細構造のデジタル表現によって表される計算領域を離れます。もちろん、これは、ウォークが計算領域の外に進むことができないため、望ましくありません。この問題を回避するために、フェーズミラーリングが使用されます。歩行者が境界を越えると、元の微細構造の再構築の鏡像である新しい領域に完全に現れます。歩行者が境界を越えるたびにデジタル再構成の完全なコピーを作成することは、コンピュータのメモリには重すぎるため、ハードウェアリソースを節約するために特別なプログラミング手法が適用されました。計算された屈曲度は、調査対象のボリュームの複雑さのみを反映するため（アノード全体ではない）、位相ミラーリングがこの方法の主な制限です。

異方性の屈曲度に基づいて、次のように定義された異方性係数を導入します。

ここでτ _x 、τ _y 、およびτ _z x の異方性屈曲係数です 、 y 、および z それぞれ方向、およびτ _r は、変位が発生する方向に関係なく、歩行者の総変位に対して計算された屈曲係数です。

結果と考察

図7は、エージングテスト中のスタックの平均端子電圧を示しています。ご覧のとおり、パフォーマンスの低下の証拠はありません。さらに、分極は最初の1000時間の動作で減少します。私たちの以前の結果は、性能の低下がないにもかかわらず、反応面の接触面が大幅に減少することを示しました[24]。 TPBの崩壊は不均一であり、スタック内の位置に強く依存していることがわかりました[24]。この論文では、微細構造の進化が不均一であるだけでなく、異方性でもあることを示します。アノードの複雑さは、図6に示されているデジタル材料表現を使用して導出された異方性の屈曲係数に基づいて推定されました。

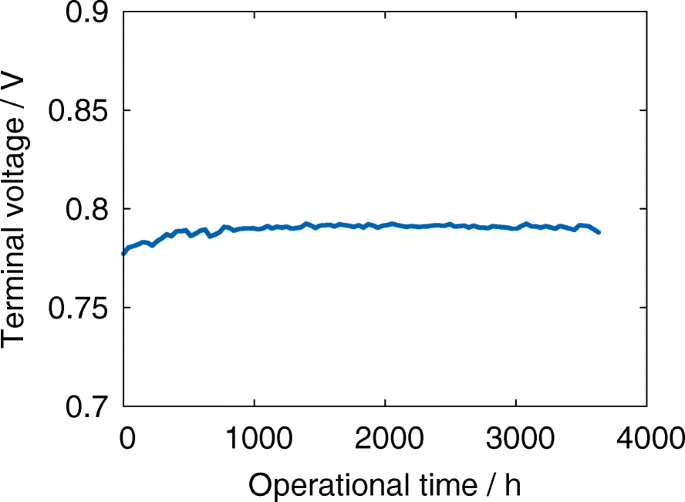
長期動作中の動作時間の関数としての端子電圧

備考 実際の実験では、得られた対象ボリュームの直径は、実験的なアーティファクトの存在により、それぞれ異なります。カーテン効果、シェード、再配置などの最も一般的なアーティファクトは、アクセス可能な断面を制限する場合があります。結果として、適切に認識され、セグメント化できるボリュームは、測定ごとに異なります。場合によっては、10個を超えるμを取得できます。 z のm 方向;ただし、カーテンは音質に影響するため、 y の画像 方向は限られていました。他の人にとっては、 y の画像は鮮明でした 方向ですが、限られた数の画像しか正しく位置合わせできませんでした。定量化のために、各ボリュームは約1000 μでした m ³ 。ただし、視覚化のために、画像を1つの一般的なサイズである10 μにトリミングしました。 m×8 μ m×5 μ mを並べて、図6で比較できるようにします。

屈曲係数推定の方法論は、「実験方法論」のセクションで簡単に紹介されました。図8は、セルとスタックのさまざまな場所の異方性係数を示しています。参照サンプルとの比較も示されています。結果に見られる一般的な傾向から、次の結論に至りました。

• 参照アノード材料は、エージングテスト中に強い異方性に変化する等方性特性を持っています。

  

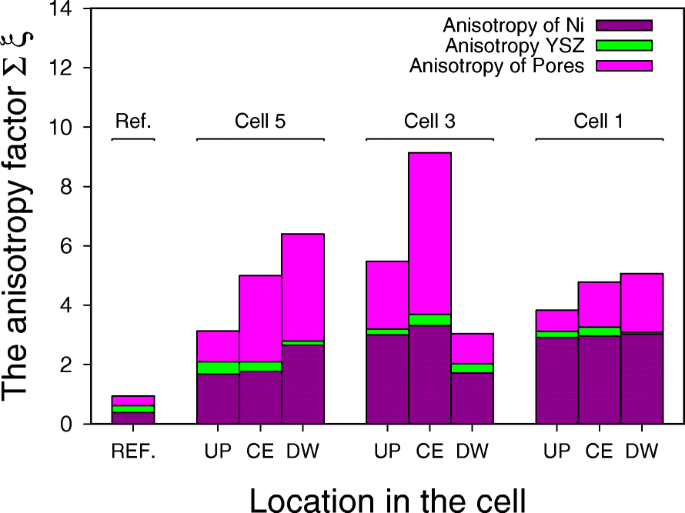
  スタック内とセル内の異なる位置での異方性係数。UP、CE、およびDWはそれぞれセルの上流​​、中央、および下流を指し、頭字語REFは参照セルに対応します

• 一般的な傾向として、異方性係数はセルの下流に移動するにつれて増加します。

• 強い異方性は、ニッケル相と細孔相でのみ観察されました。イットリウム安定化ジルコニウムは等方性のままです。

異方性の考えられる原因は、ニッケル粒子の粗大化[37–39]と、以前の研究[23、24、40]および他の研究グループ[18、41]で観察された移動です。長期間の操作中に、ニッケル粒子はアノード電解質界面からアノード表面に向かって移動します。移動は主に一方向に発生するため、微細構造の異方性につながります。それはまた、異方性がニッケル相と細孔相にのみ影響を与える理由を説明します。詳細なメカニズムは不明ですが、ニッケル粒子がアノード-電解質界面からアノード表面に向かって移動する原因として考えられるのは、水酸化ニッケルなどの揮発性ニッケル種の気化堆積です。それはニッケルの不均一性と不連続な電子伝導経路を引き起こします[42]。

今日のSOFCシミュレーションで使用されるほとんどのガス拡散モデルは、均質な多孔質電極を想定しています。ほとんどのアプリケーションで正確ですが、私たちの結果は、この均一な仮定が劣化後に成り立たない可能性があることを示しています。この記事で提示された観察の直接的な意味は、老化したサンプルの微細構造パラメータを数値シミュレーションに実装したい場合、モデルで考慮される移動現象の方向を覚えておくことが重要であるということです。結果として、微細構造パラメータから適切な異方性特性を抽出する必要があります（異方性が検出された場合）。得られた結果に基づいて、屈曲係数は拡散係数の減少率を定量的に表すため、拡散を考慮している間は異方性が特に重要であると結論付けることができます。長期間の操作後に取得されたさまざまなアノードの微細構造パラメータを並置しながら異方性の方向に注意することは、提示された観察のためのもう1つの実用的な提案です。

一般的な結論

この論文では、SOFCの長期動作がアノードの微細構造の異方性につながる可能性があることを初めて示しました。拡張発電実験は、ショートスタックを使用して実施されました。局所的に分解された微細構造分析は、FIB-SEMナノトモグラフィーを使用したエージングテストの前後に実行されました。得られたアノード微細構造の3D再構成は、異方性屈曲係数を計算するために拡散ベースのアルゴリズムに実装されました。結果は、長期間の操作により、調査したアノードのニッケル相と細孔相に強い異方性が生じたことを示しています。エージングテスト後のアノードの異方性特性の考えられる原因は、ニッケル粒子の移動、成長、および粗大化です。

データと資料の可用性

これらの調査結果を再現するために必要な生データとプロセスデータは、現在進行中の調査の一部を形成しているため、現時点では共有できません。

略語

CPOX：

接触部分酸化

FIB：

集束イオンビーム

MSTB：

モジュラースタックテストベンチ

SEM：

走査型電子顕微鏡

SOCF：

固体酸化物形燃料電池

TPB：

三重相境界

YSZ：

イットリア安定化ジルコニア