デジタルロジック機能

複数の接点を使用して、架空のランプ回路の単純な論理関数を構築し、元の「ラダー」にラングを追加することで、これらの回路を非常に簡単かつ理解できるように文書化できます。

スイッチとランプのステータスに標準のバイナリ表記を使用する場合（0は非作動または非通電、1は作動または通電）、真理値表を作成して、ロジックがどのように機能するかを示すことができます。

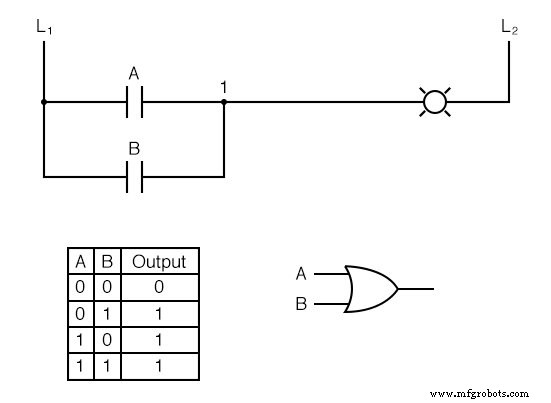
これで、接点Aまたは接点Bのいずれかが作動すると、ランプが点灯します。これは、ランプに通電するために必要なのは、ワイヤL ₁ からの電流の経路が少なくとも1つあることだけだからです。 配線1に。

私たちが持っているのは、接点とランプだけで実装された単純なOR論理関数です。

2つの接点を並列ではなく直列に配線することで、ANDロジック機能を模倣できます。

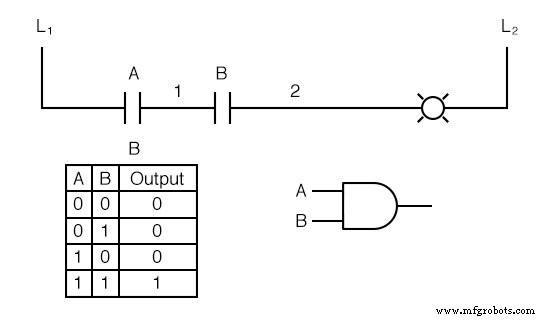
これで、Aに連絡した場合にのみランプが点灯します 接点Bが同時に作動します。

ワイヤL ₁ からの電流のパスが存在します 両方の場合に限り、ランプ（ワイヤー2）に接続します。 スイッチの接点が閉じています。

論理反転（NOT）機能は、通常開接点の代わりに通常閉接点を使用するだけで、接点入力に対して実行できます。

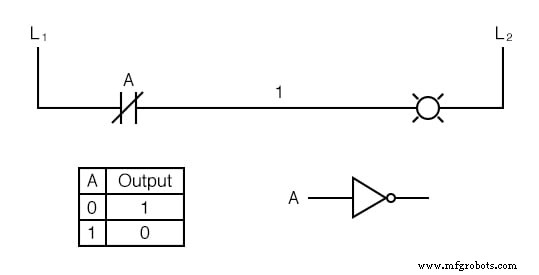
これで、接点が でない場合、ランプが点灯します。 作動し、接点が作動すると非通電になります。

OR関数を使用して、通常は閉じている接点を使用して各「入力」を反転すると、NAND関数になります。

ブール代数として知られる数学の特別な分野 、入力信号の反転に伴って変化するゲート関数の恒等写像のこの効果は、ドモルガンの定理によって説明されます。 、後の章でより詳細に検討される主題。

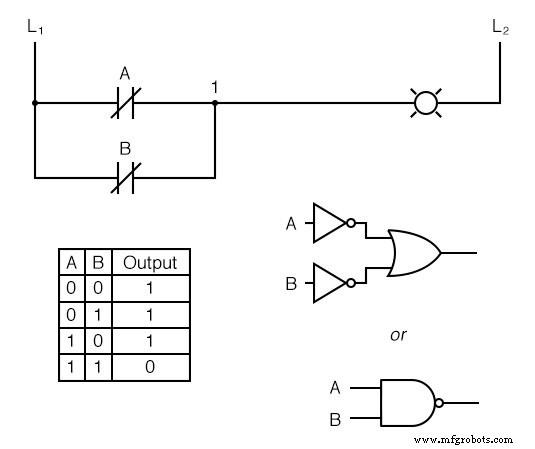
どちらかの場合、ランプが点灯します 連絡先は作動していません。 両方の場合にのみ消えます 接点は同時に作動します。

同様に、AND関数を使用して、通常は閉じている接点を使用して各「入力」を反転すると、NOR関数になります。

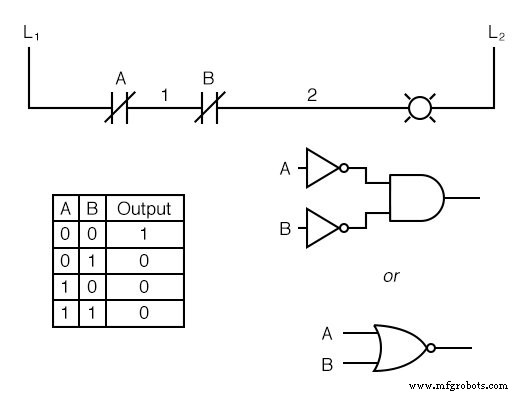
ラダー回路を対応する論理ゲートと比較すると、パターンがすぐに明らかになります。

• 並列接点はORゲートに相当します。
• 直列接点はANDゲートに相当します。
• ノーマルクローズ接点は、NOTゲート（インバーター）と同等です。

接点を直並列配置でグループ化することにより、組み合わせ論理関数を構築することもできます。次の例では、AND、OR、およびインバーター（NOT）ゲートの組み合わせから構築された排他的論理和関数があります。

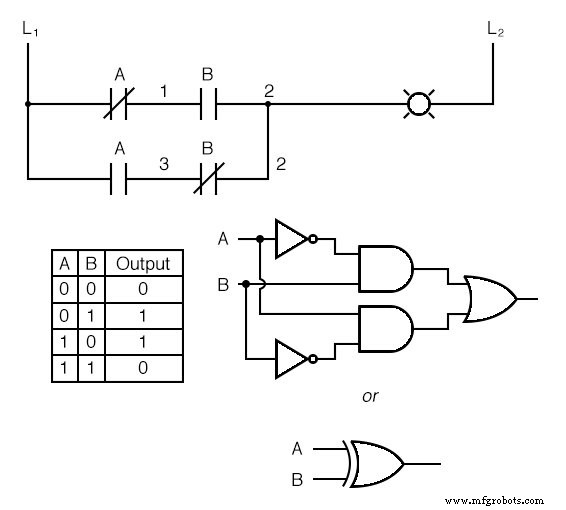
トップラング（NCコンタクトAとNOコンタクトBの直列）は、トップNOT / ANDゲートの組み合わせに相当します。

下部のラング（NC接点Bと直列のNO接点A）は、下部のNOT / ANDゲートの組み合わせに相当します。

ワイヤ番号2の2つのラング間の並列接続は、ラング1またはラング2のいずれかがランプに通電できるようにするという点で、ORゲートに相当します。

排他的論理和関数の設計

排他的論理和機能を作成するには、入力ごとに2つの接点を使用する必要がありました。1つは直接入力用で、もう1つは「反転」入力用です。

2つの「A」接点は、2つの「B」接点と同様に同じメカニズムで物理的に作動します。

連絡先間の一般的な関連付けは、連絡先のラベルで示されます。

ラダー図で使用できるスイッチまたはリレー（通常開または通常閉）の新しい接点はそれぞれ同じラベルでマークされているため、ラダー図で表すことができるスイッチあたりの接点数に制限はありません。

1つのスイッチ（またはリレー）の複数の接点が、2つの「A」ラベルではなく「A-1」や「A-2」などの複合ラベルで指定されている場合があります。

これは、各スイッチまたはリレーのどの接点セットが回路のどの部分に使用されているかを具体的に指定する場合に特に便利です。

わかりやすくするために、このレッスンではこのような手の込んだラベル付けは控えます。複数の連絡先に共通のラベルが表示されている場合は、それらの連絡先がすべて同じメカニズムで作動していることがわかります。

出力を反転したい場合 スイッチで生成されるロジック機能の場合、通常は閉じている接点を持つリレーを使用する必要があります。

たとえば、通常開接点の逆またはNOTに基づいて負荷にエネルギーを供給したい場合は、次のようにすることができます。

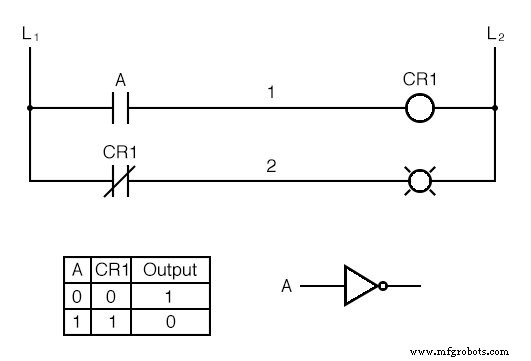
リレーを「制御リレー1」またはCR ₁ と呼びます。 。 CR ₁ のコイルの場合 （最初のラングの括弧のペアで表されます）がオンになり、2番目のラングの接点が開きます 、したがってランプの電源を切ります。

スイッチAからCR ₁ のコイルまで 、論理関数は非反転です。リレーコイルCR ₁ によって作動する通常閉接点 スイッチの作動状態とは反対のランプを駆動する論理インバータ機能を提供します。

この反転戦略を、OR-to-NANDなど、以前に作成した反転入力関数の1つに適用すると、リレーを使用して出力を反転し、非反転関数を作成できます。

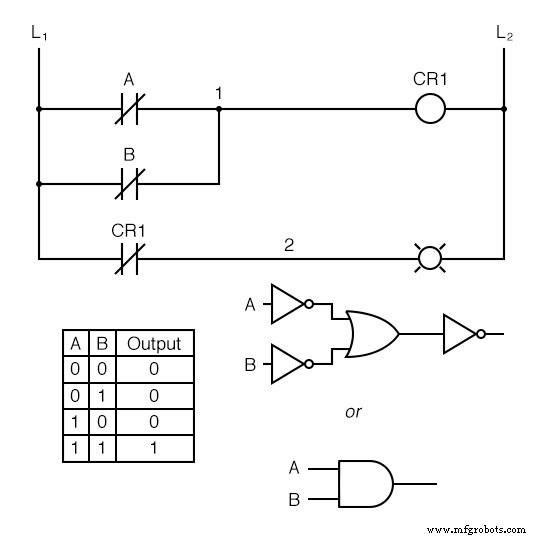
スイッチからCR ₁ のコイルまで 、論理関数はNANDゲートの論理関数です。 CR ₁ の通常閉接点は、NAND関数をAND関数に変換するための最後の反転を1つ提供します。

レビュー ：

• 並列接点は論理的にORゲートと同等です。
• 直列接点は論理的にANDゲートと同等です。
• ノーマルクローズ（N.C.）接点は、論理的にNOTゲートと同等です。
• 出力を反転するにはリレーを使用する必要があります 論理ゲート機能の機能ですが、反転ゲート入力を表すには、単純なノーマルクローズスイッチ接点で十分です。 。

関連するワークシート：

• ブール代数ワークシート
• 電気機械式リレーロジックワークシート
• デジタル論理信号ワークシート