バイナリカウントシーケンス
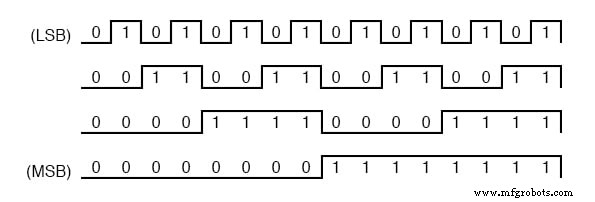
0000から1111までの4ビットのバイナリカウントシーケンスを調べると、0から1までのビットの「振動」に明確なパターンが明らかになります。

最下位ビット(LSB)がカウントシーケンスのすべてのステップで0と1の間で切り替わるのに対し、後続の各ビットは前のビットの半分の周波数で切り替わることに注意してください。
最上位ビット(MSB)は、16ステップのカウントシーケンス全体で1回だけトグルします:7(0111)と8(1000)の間の遷移時。
4ビットバイナリで「カウント」するデジタル回路を設計する場合、必要なのは一連の分周回路を設計することだけです。各回路は、方形波パルスの周波数を2倍に分周します。
J-Kフリップフロップは、J入力とK入力の両方が「ハイ」になったときにクロックパルスのコマンドで出力状態を「トグル」する機能を備えているため、このタスクに最適です(1):
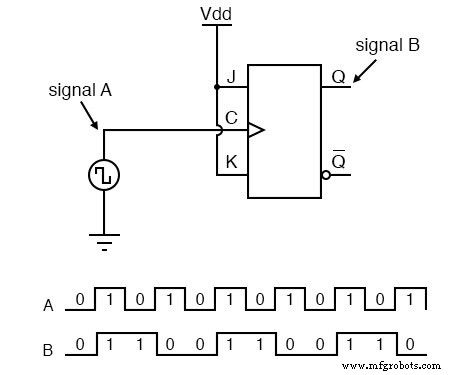
この回路の2つの信号(AとB)が2進数の2ビットを表すと考えると、信号AはLSB、信号BはMSBであり、カウントシーケンスが11から10、01まで逆方向であることがわかります。 00に戻し、再び11に戻します。
私たちが想定した方向には数えられないかもしれませんが、少なくとも数えられます!
次のセクションでは、すべてJ-Kフリップフロップで作成され、そのフリップフロップのトグル動作モードの活用に基づいた、さまざまなタイプのカウンタ回路について説明します。
レビュー:
- バイナリカウントシーケンスは、オクターブ周波数分割のパターンに従います。LSBからMSBまでの各ビットの発振周波数は、2分割パターンに従います。つまり、LSBは最高周波数で発振し、次にLSBの周波数の半分の次のビット、その前のビットの周波数の半分の次のビットなどが続きます。
- 「トグル」モードで設定されたJ-Kフリップフロップを使用して、バイナリシーケンスで「カウント」する回路を構築できます。
関連するワークシート:
- カウンターワークシート
産業技術



