コンポーネント障害分析

技術者の仕事は、誤動作している回路の「トラブルシューティング」（問題の特定と修正）を伴うことがよくあります。優れたトラブルシューティングは、要求が厳しくやりがいのある作業であり、基本的な概念の完全な理解、仮説を立てる能力（効果の提案された説明）、確率に基づいてさまざまな仮説の価値を判断する能力（1つの特定の原因の可能性）が必要です。別のものよりも優れている可能性があります）、そして問題を修正するための解決策を適用する際の創造性の感覚。

これらのスキルを科学的方法論に抽出することは可能ですが、ほとんどの実践的なトラブルシューティング担当者は、トラブルシューティングにはちょっとした芸術が含まれ、この芸術を完全に開発するには何年もの経験が必要になる可能性があることに同意します。

必要なスキルは、コンポーネントの障害がさまざまな構成の回路にどのように影響するかを、すぐに直感的に理解することです。ここでは、直列回路と並列回路の両方でのコンポーネント障害の影響のいくつかを調査し、その後、「直列-並列の直並列回路」の章の最後でさらに詳しく説明します。

単純な直列回路の故障の分析

簡単な直列回路から始めましょう：

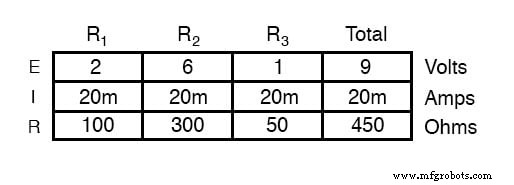
この回路のすべてのコンポーネントが適切な値で機能しているので、すべての電流と電圧降下を数学的に決定できます。

直列回路の短絡部品

ここで、R ₂ 短絡に失敗します。 短縮 これは、抵抗器がほとんどまたはまったく抵抗器のない真っ直ぐなワイヤーとして機能することを意味します。回路は、「ジャンパー」線がR ₂ に接続されているかのように動作します。 （不思議に思うかもしれませんが、「ジャンパーワイヤ」は、回路内の一時的なワイヤ接続の一般的な用語です）。 R ₂ の短絡状態の原因 この例では、私たちには関係ありません。回路への影響のみを考慮します：

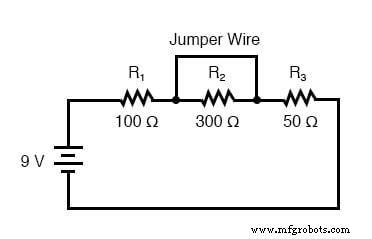
R ₂ を使用 ジャンパー線または内部抵抗器の故障のいずれかによって短絡すると、回路の総抵抗が減少します。 。バッテリーから出力される電圧は一定であるため（少なくともここでの理想的なシミュレーションでは）、総回路抵抗の減少は、総回路電流を増加させる必要があることを意味します。 ：

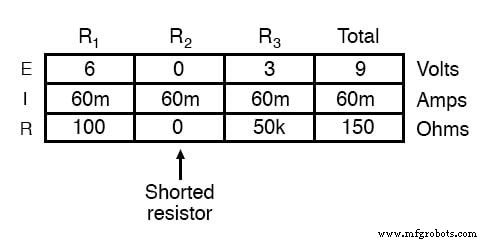
回路電流が20ミリアンペアから60ミリアンペアに増加すると、電圧はR ₁ の両端で低下します。 およびR ₃ （抵抗は変更されていません）も増加するため、2つの抵抗が9ボルト全体を降下させます。 R ₂ 、ジャンパー線の非常に低い抵抗によってバイパスされ、回路から効果的に排除され、一方のリード線からもう一方のリード線への抵抗がゼロに減少しました。したがって、R ₂ の両端の電圧降下 、合計電流を増やしても、ゼロボルトです。

直列回路で開いたコンポーネント

一方、R ₂ の場合 「オープン」に失敗すると、抵抗がほぼ無限のレベルに増加し、回路の残りの部分にも広範囲の影響が生じます。

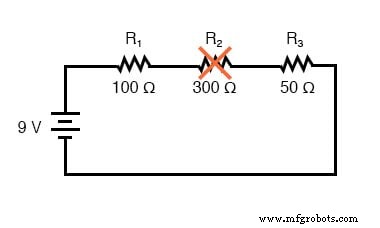
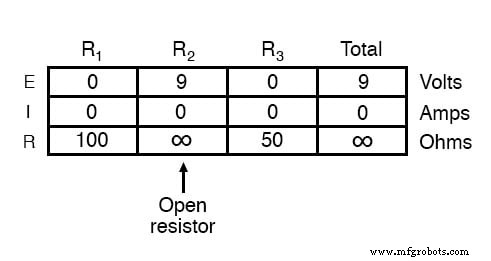
R ₂ を使用 無限抵抗と総抵抗が直列回路のすべての個々の抵抗の合計である場合、総電流はゼロに減少します。回路電流がゼロの場合、R ₁ の両端に電圧降下を発生させる電流はありません。 またはR ₃ 。 R ₂ 一方、端子間の完全な供給電圧が現れます。

単純な並列回路の障害の分析

並列回路にも同じ前後解析手法を適用できます。まず、「正常な」並列回路がどのように動作するかを決定します。

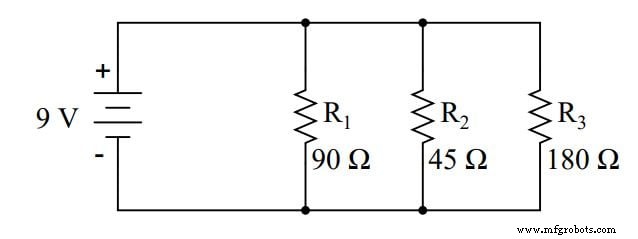
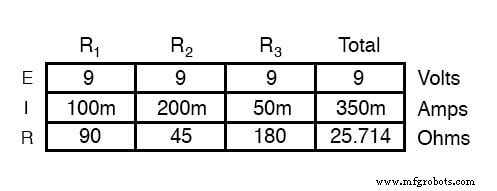
並列回路で開いたコンポーネント

R ₂ この並列回路で開きます。効果は次のとおりです。

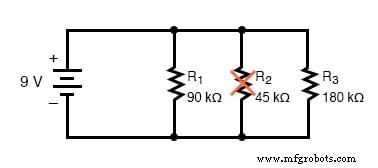
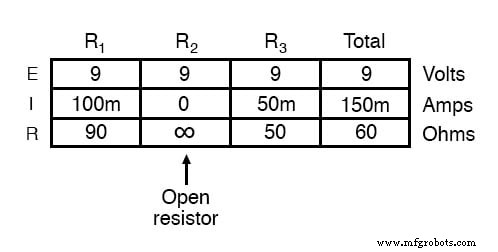
この並列回路では、開いた分岐はその分岐を流れる電流と回路の合計電流にのみ影響することに注意してください。合計電圧—並列回路内のすべてのコンポーネント間で均等に共有されるため、すべての抵抗器で同じになります。電圧源の傾向は電圧を一定に保つことであるという事実のため 、その電圧は変化せず、すべての抵抗器と並列であるため、すべての抵抗器の電圧を以前と同じ9ボルトに保持します。その電圧が並列回路の唯一の一般的なパラメータであり、他の抵抗器は抵抗値を変更していないため、それぞれの分岐電流は変更されません。

家庭用照明アプリケーション

これは家庭用ランプ回路で起こることです。すべてのランプは、並列に配置された電源配線から動作電圧を取得します。 1つのランプのオンとオフ（並列回路の1つの分岐の開閉）は、部屋の他のランプの動作には影響しません。その1つのランプの電流（分岐回路）と、すべてのランプに電力を供給する合計電流のみが影響します。部屋：

並列回路の短いコンポーネント

理想的なケース（完全な電圧源とゼロ抵抗接続ワイヤを使用）では、単純な並列回路で抵抗を短絡しても、回路の他の分岐で何が起こっているかに影響を与えません。実生活では、効果はまったく同じではありません。その理由は次の例でわかります。

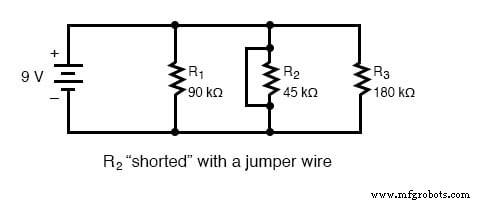
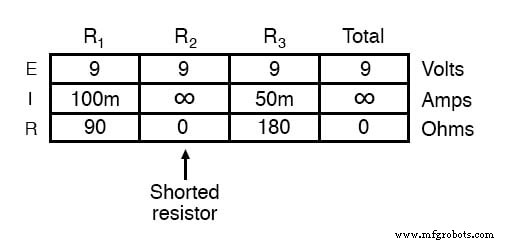
短絡した抵抗（抵抗0Ω）は、理論的には、任意の有限の電圧源（I =E / 0）から無限の電流を引き出します。この場合、R ₂ のゼロ抵抗 回路の総抵抗もゼロΩに減少し、総電流が無限大の値に増加します。ただし、電圧源が9ボルトで安定している限り、他の分岐電流（I _R1 およびI _R3 ）変更されません。

分析における非理想的な仮定

ただし、この「完全な」スキームの重要な前提は、短絡負荷に無限の量の電流を供給しながら、電圧供給が定格電圧で安定した状態を維持することです。これは単に現実的ではありません。短絡の抵抗が（完全にゼロの抵抗ではなく）少量であっても、実際の 電圧源は、任意に巨大な過負荷電流を供給し、同時に安定した電圧を維持することができます。

これは主に、すべての電源に固有の内部抵抗によるものであり、それらが構成されている材料の避けられない物理的特性に起因します。

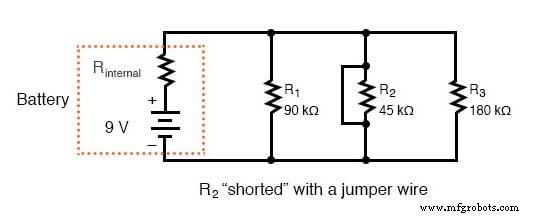
これらの内部抵抗は、小さいかもしれませんが、単純な並列回路を直並列の組み合わせ回路に変えます。通常、電圧源の内部抵抗は十分に低いため無視できますが、コンポーネントの短絡による大電流が発生すると、その影響が非常に顕著になります。

この場合、短絡したR ₂ その結果、ほとんどすべての電圧がバッテリーの内部抵抗の両端で降下し、抵抗R ₁ にほとんど電圧が残りません。 、R ₂ 、およびR ₃ ：

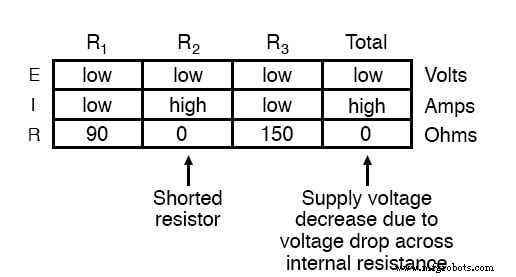
言うまでもなく、電圧源の端子間の意図的な直接短絡は悪い考えです。結果として生じる大電流（熱、フラッシュ、火花）が近くの人に害を及ぼさない場合でも、ほとんどの電圧源ではない短絡を処理するように特別に設計されていない限り、電圧源は損傷を受ける可能性があります。

>

最終的に、この本では、数値を使用せずに回路の分析を紹介します。 つまり、バッテリーが何ボルトを生成するか、各抵抗器に何オームの抵抗があるかなどを正確に知らずに、回路のコンポーネント障害の影響を分析します。このセクションは、その種の分析の導入ステップとして機能します。

一方、オームの法則と直列および並列回路の規則の通常の適用は、数値（「定量的」）で実行されます。 ）、正確な数値のないこの新しい種類の分析は、私が定性的と呼んでいるものです。 分析。つまり、品質を分析します。 正確な量ではなく、回路内の効果の 。その結果、電気回路の動作をより深く直感的に理解できるようになります。

レビュー：

• コンポーネントに障害が発生した場合に回路で何が起こるかを判断するには、障害が発生したコンポーネントの等価抵抗を使用して回路を再描画し、すべての値を再計算します。
• 特定のコンポーネントに障害が発生した回路に何が起こるかを直感的に判断する機能は、重要です。 電子機器のトラブルシューティング担当者が開発するスキル。学ぶための最良の方法は、回路計算と実際の回路を実験し、障害によって何が変化するか、何が変わらないか、そして理由に細心の注意を払うことです。 ！
• ショート コンポーネントは、抵抗が劇的に減少したコンポーネントです。
• オープン コンポーネントは、抵抗が劇的に増加したコンポーネントです。記録として、抵抗器は短絡に失敗するよりも頻繁に開放に失敗する傾向があり、物理的または電気的に過大なストレス（物理的に乱用または過熱）されない限り、抵抗はほとんど失敗しません。

関連ワークシート：

• 基本回路トラブルシューティングワークシート