重ね合わせの原理–解決された例による回路解析

重ね合わせの原理–解決された例を使用したステップバイステップガイド

重ね合わせの原理とは何ですか？

重ね合わせの原理 多数のエネルギー源を持つ複雑なネットワークを解決するために使用されます。各ソースの効果を個別に計算することにより、要素間の電圧と電流を決定することが重要な概念です。そして、すべてのソースの効果を組み合わせて、回路要素の実際の電圧と電流を取得します。

重ね合わせの原理は次のように述べています;

つまり、一度に1つの独立したソースのみが動作していると見なします。したがって、他のソースを削除する必要があります。理想的な電源のために、電圧源は短絡され、電流源は開回路になっています。ソースの内部抵抗が与えられている場合は、回路を考慮する必要があります。

重ね合わせの原理は、オームの法則に従う回路にのみ適用されます。

関連記事：テブナンの定理。解決例を含むステップバイステップガイド

重ね合わせの原理を使用する場合

重ね合わせの原理を適用するには、ネットワークは以下の要件に従う必要があります。

回路で使用されるコンポーネントは線形である必要があります。つまり、抵抗器の場合、電流の流れは電圧に比例します。インダクタの場合、磁束リンケージは電流に比例します。したがって、抵抗、インダクタ、およびコンデンサは線形要素です。しかし、ダイオード、トランジスタは線形要素ではありません。
回路コンポーネントは両側要素である必要があります。つまり、電流の大きさはエネルギー源の極性とは無関係です。
重ね合わせの原理の助けを借りて、電流が要素を通過すること、抵抗の電圧降下、およびノード電圧を見つけることができます。しかし、要素から消費される電力を見つけることはできません。

関連記事：ノートンの定理。解決例を含むステップバイステップガイド

重ね合わせの原理に従うための手順

ステップ-1 ネットワークで利用可能な独立した情報源の数を調べてください。

ステップ2 いずれか1つのソースを選択し、他のすべてのソースを削除します。ネットワークが依存ソースで構成されている場合、それを排除することはできません。計算中はそのままです。

すべてのエネルギー源が理想的なエネルギー源であると考えている場合は、内部抵抗を考慮する必要はありません。そして、電圧源と開回路電流源を直接短絡します。ただし、ソースの内部抵抗が指定されている場合は、内部抵抗を交換する必要があります。

ステップ3 現在、回路には、独立したエネルギー源が1つだけ存在します。回路内のエネルギー源が1つだけの応答を見つける必要があります。

ステップ4 ネットワークで利用可能なすべてのエネルギー源について、手順2と3を繰り返します。独立したソースが3つある場合は、これらの手順を3回繰り返す必要があります。そして、あなたが応答の価値を得るたびに。

ステップ5 ここで、個々のソースによって取得された代数的合計によってすべての応答を結合します。そして、ネットワークの特定の要素に対する応答の最終値を取得します。他の要素に対する応答を見つける必要がある場合は、その要素に対してこれらの手順を再度実行する必要があります。

関連記事：SUPERMESH回路解析–解決された例を使用したステップバイステップ

重ね合わせの原理を解いた例

例：

重ね合わせの原理の働きを例で理解しましょう。現在の（I _L ）重ね合わせの原理を使用して、特定のネットワークの8Ω抵抗を通過します。

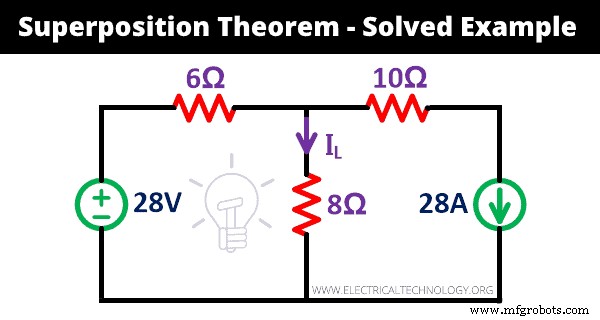
解決策：

ステップ-1 上記のネットワークに示されているように、1つの電圧源と1つの電流源が与えられています。したがって、この手順を2回繰り返す必要があります。

ステップ2 まず、28Vの電圧源がネットワークに存在すると考えます。そのため、開回路端子で電流源を取り除く必要があります。ここでのように、電流源を理想的な電流源と見なします。したがって、内部抵抗を接続する必要はありません。

残りの回路は次の図のようになります。

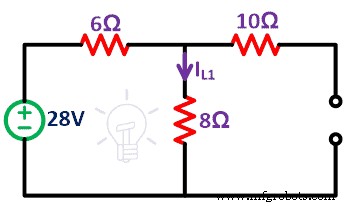
ステップ3 現在の（I _L1 ）8Ω抵抗を通過します。電圧源の効果のみを与えます。

電流源が開回路であるため、10Ωの抵抗には電流が流れません。したがって、ネットワークは1つのループのみで構成されます。

ループにKVLを適用します;

28 =6私 _{L 1} +8私 _{L 1}

28 =14 I _{L 1}

私 _{L 1} =28/14

私 _{L 1} =2A

ステップ4 ここで、現在のソースに対して同じ手順を繰り返します。この状態で、短絡により電圧源を除去します。残りの回路は下図のようになります。

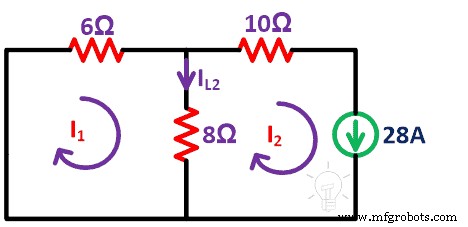
ここでは、2つのループを考慮する必要があります。 I ₁ およびI₂ ループ電流です。そして、現在のI _L2を見つけます。

ループ1にKVLを適用します;

0 =6私 ₁ +8私 ₁ –8私 ₂

14 I ₁ –8私 ₂ =0

電流がループを通過します-2は、電流源から計算されます。そしてそれはそうなるでしょう;

私 ₂ =28A

この値を上記の式に入れます;

14 I ₁ – 8（28）=0

私 ₁ =16A

現在、8Ωの抵抗ブランチは両方のループで共通です。したがって、結果として生じる電流（I _L2）を見つける必要があります。）8Ωレジスターを通過します。

私 _{L 2} =私 ₁ –私 ₂

私 _{L 2} =16 – 28

私 _{L 2} =-12A

ステップ5 ここで、電流の代数的合計によって両方のソースの効果を組み合わせます。したがって、8Ω抵抗を通過する合計電流はI _Lです。。ここでは、電流の方向が最も重要です。現在のI_L2 マイナス記号があります。これは、28Aのソースの間、電流が反対方向に流れることを意味します。そして、方向を変えることはできません。これが、すべてのソースを組み合わせながら、代数的な合計を行う理由です。

私 _L = I _L ₁ – I _L ₂

私 _L =2 +（-12）

私 _L =-10A

ここでは、8Ω抵抗を流れる電流が図に示す矢印の方向であると仮定しています。マイナス記号は反対方向を示します。そして電流量は8Aです。

関連記事：SUPERNODE回路分析–解決された例を使用したステップバイステップ

重ね合わせの原理実験

重ね合わせの原理の実験は、次の手順で実行できます。

目的

抵抗器を流れる電流を決定し、重ね合わせの原理を検証します。

必要なコンポーネント

DCソース、抵抗、DCマルチメータ、接続ワイヤ、ブレッドボードなど

理論

重ね合わせの原理は、回路解析で使用され、特定の回路の要素間の電流と電圧を検出します。この定理は、ソースの数が多い場合に役立ちます。

重ね合わせの原理によると、要素の応答は、個々のエネルギー源からの応答の代数的な合計です。

最初に、特定のネットワークの抵抗を通過する電流を計算します。すべてのソースが接続されている場合。その後、ソースを削除し、個々のソースの電流を見つけます。最後に、個々のソースから測定された電流の合計は、すべてのソースが接続されている現在の測定値と同様です。

手順

次の図に示す線形双方向回路を検討します。

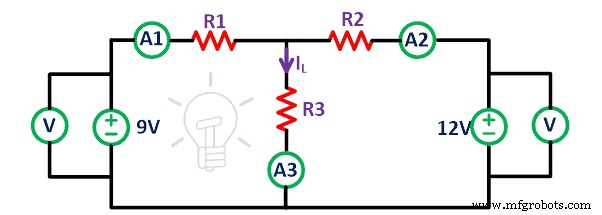
上記の回路で指定されているように、接続ワイヤを使用してブレッドボード上のすべての要素を接続します。電流計をすべての抵抗器に接続して、電流が抵抗器を通過することを確認します。ここでは、2つの電圧源があります。

最初のケースでは、両方の電圧源が回路に存在するときにすべての抵抗を通過する電流を測定します。抵抗R₁を流れる電流、R ₂ 、およびR ₃ 私です ₁ 、私 ₂ 、および私 ₃ それぞれ。

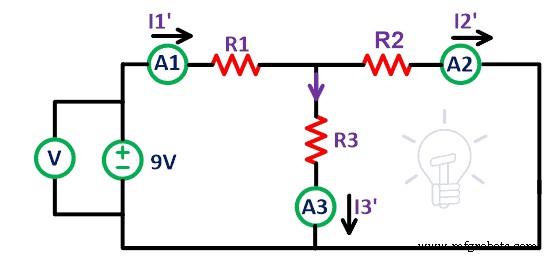
次に、回路から12V電圧源を取り外します。上図のように端子A'とB'を短絡します。ここでは、電圧源が理想的であると仮定しています。したがって、内部抵抗を接続する必要はありません。次に、現在の Iを測定します _1' 、私 _2' および私 _3' これは、それぞれ抵抗R1、R2、およびR3を通過する電流です。

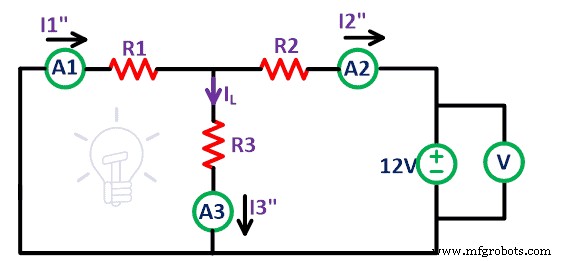
同様に、9V電圧源を取り外すと、残りの回路は上の図のようになります。ここでも、すべての抵抗を流れる電流を測定し、 Iという名前を付けます。 ₁ _“ 、私 ₂ _“ 、および私 ₃ _“ 。

関連記事： ACおよびDC回路の最大電力伝達定理

すべての値を観測テーブルの下に置きます。

観測テーブル

ソース接続	R ₁	R ₂	R ₃
両方のソースが接続されています	私 ₁	私 ₂	私 ₃
12Vのみが接続されています	私 _1'	私 _2'	私 _3'
9Vのみが接続されています	私 _1″	私 _2″	私 _3″