ACコンデンサ回路

コンデンサ対抵抗器

コンデンサは抵抗と同じようには動作しません。抵抗器は電圧降下に正比例して電子の流れを許容しますが、コンデンサは変化に対抗します。 新しい電圧レベルまで充電または放電するときに電流を引き込むか供給することにより、電圧を下げます。

コンデンサを「通過する」電子の流れは、変化率に正比例します。 コンデンサの両端の電圧の。電圧変化に対するこの反対は、リアクタンスの別の形式です。 、しかしインダクタによって示される種類とは正反対のものです。

コンデンサ回路の特性

数学的に表現すると、コンデンサを「流れる」電流とコンデンサ両端の電圧変化率の関係は次のようになります。

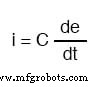
式 de / dt は微積分からのもので、1秒あたりのボルト数で表した瞬間電圧（e）の経時変化率を意味します。静電容量（C）はファラッド単位で、瞬時電流（i）はもちろんアンペア単位です。

時間の経過に伴う瞬間的な電圧変化率は、de / dtではなくdv / dtで表されることがあります。代わりに小文字の「v」または「e」を使用して電圧を表しますが、これはまったく同じことを意味します。交流で何が起こるかを示すために、簡単なコンデンサ回路を分析してみましょう：

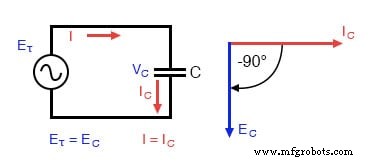
純粋な容量性回路：コンデンサの電圧はコンデンサの電流より90°遅れます

この非常に単純な回路の電流と電圧をプロットすると、次のようになります。

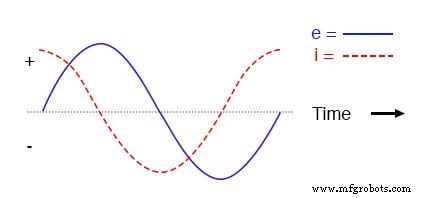
純粋な容量性回路波形。

コンデンサを流れる電流は、変化に対する反応であることを忘れないでください 両端の電圧で。

したがって、瞬時電圧がピーク（電圧正弦波のゼロ変化またはレベルスロープ）にあるときは常に瞬時電流はゼロであり、瞬時電圧が最大変化にあるときはどこでも瞬時電流はピークになります（電圧波の最も急な勾配で、ゼロラインと交差します。

これにより、現在の波と-90°位相がずれた電圧波が発生します。グラフを見ると、現在の波は電圧波に対して「有利なスタート」を持っているように見えます。電流は電圧を「リード」し、電圧は電流より「遅れ」ます。

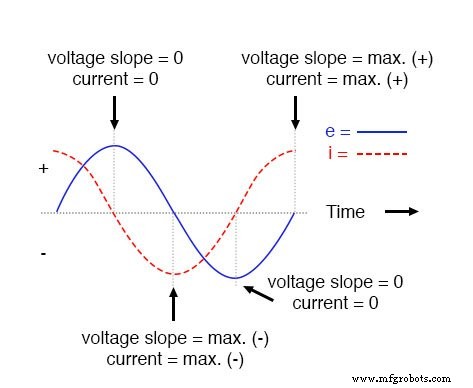
純粋な容量性回路では、電圧は電流より90°遅れます。

ご想像のとおり、単純なインダクタ回路で見たのと同じ異常な電力波が、単純なコンデンサ回路にも存在します。

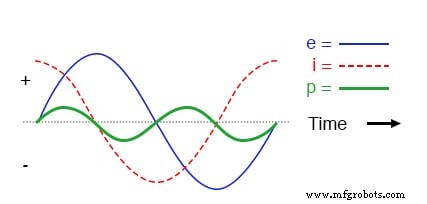
純粋な容量性回路では、瞬時電力は正または負の場合があります。

単純なインダクタ回路と同様に、電圧と電流の間の90度の位相シフトにより、正と負の間で均等に交互に変化する電力波が発生します。これは、コンデンサが電圧の変化に反応するときに電力を消費しないことを意味します。電力を交互に吸収および解放するだけです。

コンデンサのリアクタンス

電圧の変化に対するコンデンサの反対は、一般に交流電圧に対する反対に変換されます。これは、定義上、常に瞬間的な大きさと方向に変化します。

特定の周波数での特定の大きさのAC電圧に対して、特定のサイズのコンデンサは特定の大きさのAC電流を「伝導」します。

抵抗を流れる電流が抵抗の両端の電圧と抵抗によって提供される抵抗の関数であるように、コンデンサを流れるAC電流は、抵抗の両端のAC電圧とリアクタンスの関数です。 コンデンサによって提供されます。

インダクタと同様に、コンデンサのリアクタンスはオームで表され、文字X（またはより具体的にはXC）で表されます。

コンデンサは電圧変化の速度に比例して電流を「伝導」するため、変化の速い電圧ではより多くの電流を流し（より短い時間で同じ電圧ピークに充電および放電するため）、変化の遅い電圧ではより少ない電流を流します。

これが意味するのは、コンデンサのリアクタンス（オーム）は逆に 交流の周波数に比例します。

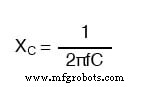
100 uFコンデンサのリアクタンス：

頻度（ヘルツ） リアクタンス（オーム） 6026.525812013.262925000.6366

容量性リアクタンスと周波数の関係は、誘導性リアクタンスの関係とは正反対であることに注意してください。

容量性リアクタンス（オーム）は、AC周波数の増加とともに減少します。逆に、誘導性リアクタンス（オーム）は、AC周波数の増加とともに増加します。インダクタは、より大きな電圧降下を生成することにより、より速く変化する電流に対抗します。コンデンサは、より大きな電流を許容することにより、より速く変化する電圧降下に対抗します。

インダクタと同様に、リアクタンス方程式の2πf項は、ギリシャ文字の小文字のオメガ（ω）に置き換えることができます。これは、角速度と呼ばれます。 AC回路の。したがって、方程式XC =1 /（2πfC）はXC =1 /（ωC）と書くこともでき、ωはラジアン/秒の単位でキャストされます。 。

単純な容量性回路の交流電流は、電圧（ボルト単位）を容量性リアクタンス（オーム単位）で割ったものに等しく、単純な抵抗性回路の交流または直流は、電圧（ボルト単位）を電圧（ボルト単位）で割った値に等しくなります。抵抗（オーム単位）。次の回路は、この数学的関係を例で示しています。

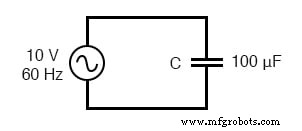
容量性リアクタンス。

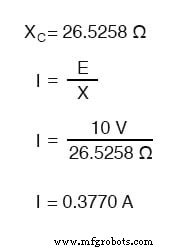
ただし、ここでは電圧と電流が同相ではないことに注意する必要があります。前に示したように、電流は電圧に対して+ 90°の位相シフトを持っています。電圧と電流のこれらの位相角を数学的に表すと、電流に対するコンデンサの無効な反対の位相角を計算できます。

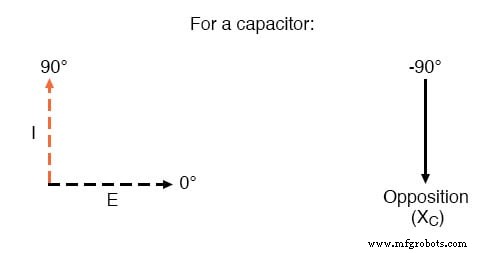
コンデンサの電圧は電流より90°遅れます。

数学的には、コンデンサの電流に対する反対の位相角は-90°であると言います。これは、コンデンサの電流に対する反対が負の虚数であることを意味します。 （上の図を参照してください。）電流に対する無効な反対のこの位相角は、回路解析、特にリアクタンスと抵抗が相互作用する複雑なAC回路の場合に非常に重要になります。

任意のを表すことは有益であることがわかります 抵抗とリアクタンスのスカラー量だけでなく、複素数の観点からの電流に対するコンポーネントの反対。

レビュー：

• 容量性リアクタンス は、コンデンサが位相シフトされた蓄積と電界でのエネルギーの放出のために交流に提供する反対です。リアクタンスは大文字の「X」で表され、抵抗（R）と同じようにオームで測定されます。
• 容量性リアクタンスは、次の式を使用して計算できます：XC =1 /（2πfC）
• 容量性リアクタンス減少 頻度が高くなります。言い換えれば、周波数が高いほど、AC電流に対抗することが少なくなります（より多く「伝導」します）。

関連するワークシート：

• コンデンサワークシート