ACインダクタ回路

抵抗とインダクタ

インダクタは抵抗と同じようには動作しません。抵抗器は（電流に正比例する電圧を下げることによって）抵抗器を流れる電流に対抗するだけですが、インダクターは変化に対抗します。 変化率に正比例する電圧を下げることにより、それらを流れる電流を 電流の。

レンツの法則に準拠 、この誘導電圧は常に電流を現在の値に維持しようとするような極性です。つまり、電流の大きさが増加している場合、誘導電圧は電流の流れを「押し」ます。電流が減少している場合、極性が反転し、電流を「押して」減少に対抗します。

現在の変化に対するこの反対は、リアクタンスと呼ばれます。 、抵抗ではなく。数学的に表現すると、インダクタの両端で降下する電圧とインダクタを流れる電流の変化率の関係は次のようになります。

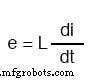
単純な誘導回路の交流

式 di / dt 微積分からの1つであり、1秒あたりのアンペアで表した、時間の経過に伴う瞬時電流（i）の変化率を意味します。

インダクタンス（L）はヘンリー単位であり、瞬時電圧（e）はもちろんボルト単位です。 「e」（v =L di / dt）ではなく「v」で表される瞬時電圧の割合を見つけることがありますが、それはまったく同じことを意味します。

交流で何が起こるかを示すために、簡単なインダクタ回路を分析してみましょう：

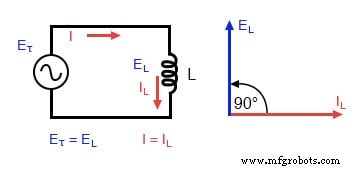
純粋な誘導回路：インダクタ電流はインダクタ電圧より90°遅れます。

この非常に単純な回路の電流と電圧をプロットすると、次のようになります。

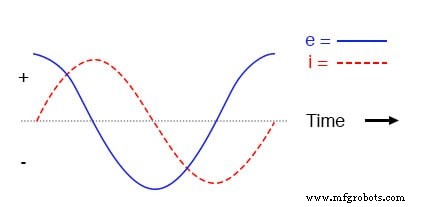
純粋な誘導回路、波形。

インダクタの両端で降下する電圧は、変化に対する反応であることを忘れないでください。 電流が流れています。

したがって、瞬時電流がピーク（電流正弦波のゼロ変化またはレベルスロープ）にあるときは常に瞬時電圧はゼロであり、瞬時電流が最大変化にあるときはどこでも瞬時電圧はピークになります（ゼロラインと交差する現在の波の最も急な勾配。

これにより、電流波と90°位相がずれた電圧波が発生します。グラフを見ると、電圧波は現在の波に対して「有利なスタート」を持っているように見えます。電圧は電流を「リード」し、電流は電圧より「遅れ」ます。

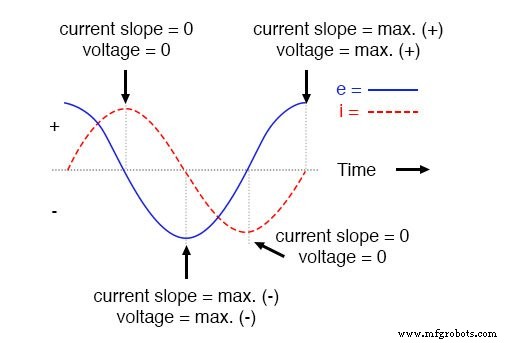
純粋な誘導回路では、電流が電圧より90°遅れます。

この回路の電力をプロットすると、事態はさらに興味深いものになります。

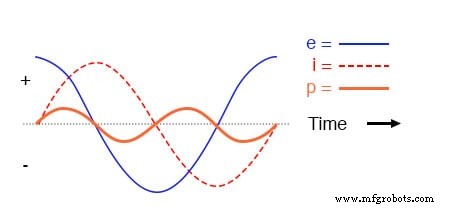
純粋な誘導回路では、瞬時電力は正または負の場合があります。

瞬時電力は瞬時電圧と瞬時電流（p =ie）の積であるため、瞬時電流またはの場合は常に電力はゼロになります。 電圧はゼロです。瞬時電流と瞬時電圧の両方が正（線より上）の場合は常に、電力は正です。

抵抗器の例と同様に、瞬時電流と電圧が両方とも負の場合（ラインの下）、電力も正になります。

ただし、電流波と電圧波は90度位相がずれているため、一方が正でもう一方が負である場合があり、その結果、負の瞬時電力が同じように頻繁に発生します。 。

負の力とは何ですか？

しかし、ネガティブは何ですか パワーはどういう意味ですか？これは、インダクタが回路に電力を放出していることを意味し、正の電力は回路から電力を吸収していることを意味します。

正と負のパワーサイクルは時間の経過とともに大きさと持続時間が等しいため、インダクタは完全なサイクルのスパンにわたって吸収するのと同じ量の電力を回路に放出します。

これが実際的な意味で意味するのは、インダクタのリアクタンスは、熱の形でエネルギーを放散する抵抗器の抵抗とはまったく異なり、ゼロの正味エネルギーを放散するということです。念のために言っておきますが、これは完全なインダクターのみであり、ワイヤー抵抗はありません。

リアクタンスと抵抗

電流の変化に対するインダクタの反対は、一般に交流に対する反対に変換されます。これは、定義上、常に瞬間的な大きさと方向に変化します。

交流に対するこの反対は、抵抗に似ていますが、常に電流と電圧の間の位相シフトをもたらし、ゼロ電力を消費するという点で異なります。違いがあるため、名前は異なります：リアクタンス 。 ACに対するリアクタンスは、抵抗と同じようにオームで表されますが、数学記号がRではなくXである点が異なります。

具体的には、インダクタに関連するリアクタンスは通常、大文字のXで表され、下付き文字は次のようになります。X _L 。

インダクタは電流の変化率に比例して電圧を降下させるため、電流の変化が速い場合は電圧が降下し、電流の変化が遅い場合は電圧が降下します。これが意味するのは、インダクタのリアクタンス（オーム）は交流の周波数に正比例するということです。リアクタンスを決定するための正確な式は次のとおりです。

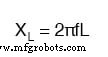
10 mHのインダクタを60、120、および2500 Hzの周波数にさらすと、下の表にリアクタンスが現れます。

10 mHインダクタのリアクタンス：

頻度（ヘルツ） リアクタンス（オーム） 603.76991207.53982500157.0796

リアクタンス方程式では、「2πf」（Lを除く右側のすべて）という用語は、それ自体に特別な意味を持っています。完全な円の回転を表すACの1サイクルを想像すると、交流が「回転」しているのは1秒あたりのラジアン数です。

ラジアン は角度測定の単位です。完全な円に360°があるのと同じように、1つの完全な円に2πラジアンがあります。 ACを生成するオルタネーターが2極ユニットの場合、シャフトが1回転するごとに1サイクル、つまり2πラジアンまたは360°ごとに生成されます。

この2πの定数にヘルツ単位の周波数（1秒あたりのサイクル数）を掛けると、結果は1秒あたりのラジアン単位の数値になります。これは角速度として知られています。 ACシステムの。

ACシステムの角速度

角速度は、式2πfで表すことも、独自の記号であるギリシャ文字の小文字のオメガで表すこともできます。これは、ローマ字の小文字の「w」：ωに似ています。したがって、リアクタンス式X _L =2πfLはX _L と書くこともできます =ωL。

この「角速度」は、AC波形がどれだけ速く循環しているかを表したものであり、全周期は2πラジアンに等しいことを理解する必要があります。これは、ACを生成するオルタネーターの実際のシャフト速度を必ずしも表すものではありません。

オルタネーターに3つ以上の極がある場合、角速度はシャフト速度の倍数になります。このため、ωは電気の単位で表されることがあります。 機械的な動きと区別するために、1秒あたりの（単純な）ラジアンではなく1秒あたりのラジアン。

システムの角速度をどのように表現しても、インダクタのリアクタンスに正比例することは明らかです。 ACシステムで周波数（またはオルタネーターのシャフト速度）が増加すると、インダクターは電流の通過に対してより大きな反対を提供し、その逆も同様です。

単純な誘導回路の交流電流は、電圧（ボルト単位）を誘導性リアクタンス（オーム単位）で割ったものに等しくなります。同様に、単純な抵抗回路の交流電流または直流電流は、電圧（ボルト単位）を電圧（ボルト単位）で割った値に等しくなります。抵抗（オーム単位）。回路例を次に示します：

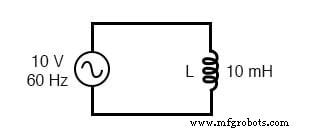
誘導性リアクタンス

位相角

ただし、ここでは電圧と電流が同相ではないことに注意する必要があります。前に示したように、電圧は電流に対して+ 90°の位相シフトを持っています。これらの電圧と電流の位相角を複素数の形式で数学的に表すと、インダクタの電流に対する反対の位相角もあることがわかります。

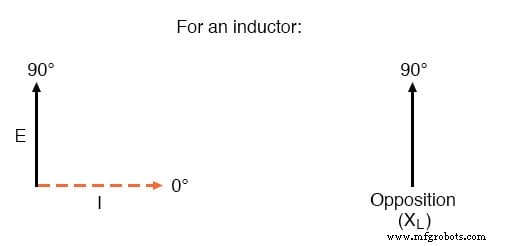
インダクタの電流は電圧より90°遅れます。

数学的には、インダクタの電流に対する反対の位相角は90°であると言います。これは、インダクタの電流に対する反対が正の虚数であることを意味します。電流に対する無効な反対のこの位相角は、特にリアクタンスと抵抗が相互作用する複雑なAC回路の場合、回路解析で非常に重要になります。

任意のを表すことは有益であることがわかります 抵抗とリアクタンスのスカラー量ではなく、複素数の観点からの電流に対するコンポーネントの反対。

レビュー：

• 誘導性リアクタンス は、インダクタが位相シフトされた蓄積と磁場内のエネルギーの放出のために交流に提供する反対です。リアクタンスは大文字の「X」で表され、抵抗（R）と同じようにオームで測定されます。
• 誘導性リアクタンスは、次の式を使用して計算できます：X _L =2πfL
• 角速度 AC回路の周波数は、1秒あたりのサイクル数ではなく、1秒あたりの電気ラジアンの単位で周波数を表す別の方法です。ギリシャ文字の小文字「オメガ」またはωで象徴されています。
• 誘導性リアクタンス増加 頻度が高くなります。言い換えれば、周波数が高いほど、電子のACフローに対抗します。

関連するワークシート：

• インダクタワークシート
• 誘導性リアクタンスワークシート