レゾナントフィルター
これまで、私たちが集中してきたフィルター設計は、どちらかを採用してきました。 コンデンサまたは インダクタですが、同時に両方を使用することはできません。 LとCの組み合わせは共振する傾向があり、この特性はバンドパスおよびバンドストップフィルター回路の設計に利用できることを今では知っておく必要があります。
直列LC回路は共振時に最小のインピーダンスを与え、並列LC(「タンク」)回路はそれらの共振周波数で最大のインピーダンスを与えます。これを知っているので、バンドパスフィルターまたはバンドストップフィルターのいずれかを設計するための2つの基本的な戦略があります。
バンドパスフィルターの場合、2つの基本的な共振戦略は次のとおりです。信号を渡すための直列LC、または信号を短絡するための並列LCです。ここでは、2つのスキームを対比してシミュレーションします:
シリーズレゾナントバンドパスフィルター
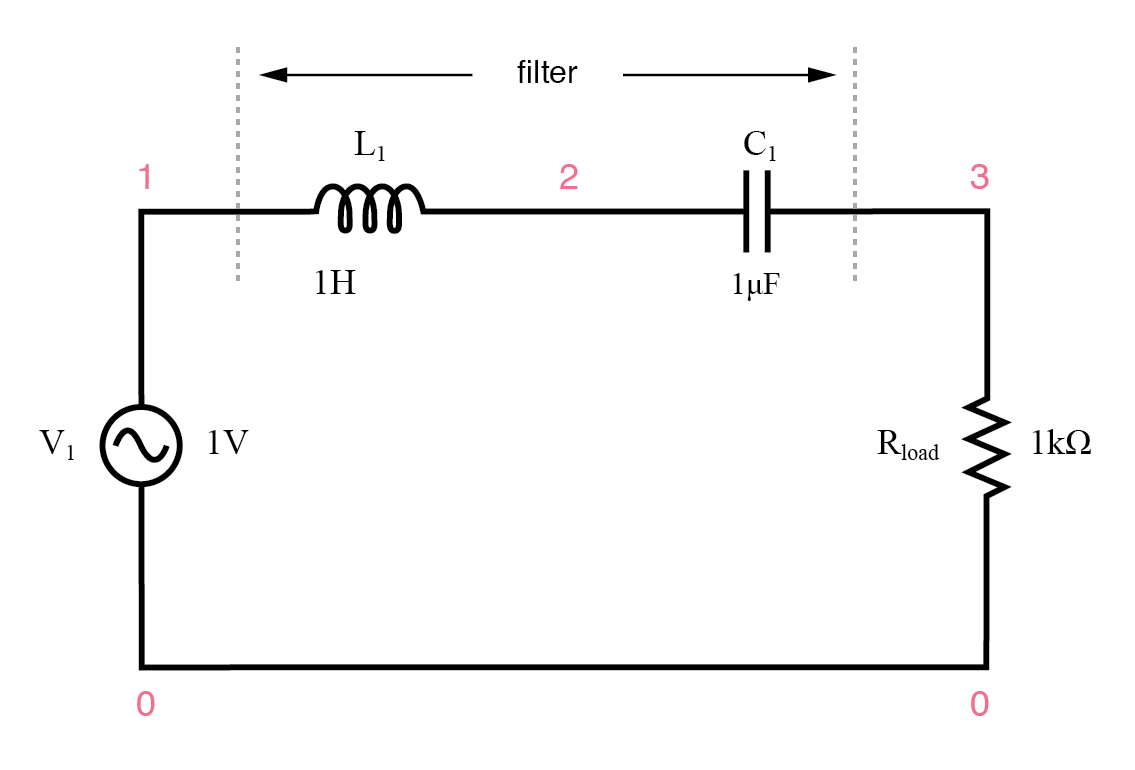
直列共振LCバンドパスフィルター。
直列LCコンポーネントは、共振時に信号を渡し、他の周波数の信号が負荷に到達するのをブロックします。
シリーズレゾナントバンドパスフィルター v1 1 0 ac 1 sin l1 1 2 1 c1 2 3 1u rload 3 0 1k .ac lin 20 50 250 .plot ac v(3) 。終わり
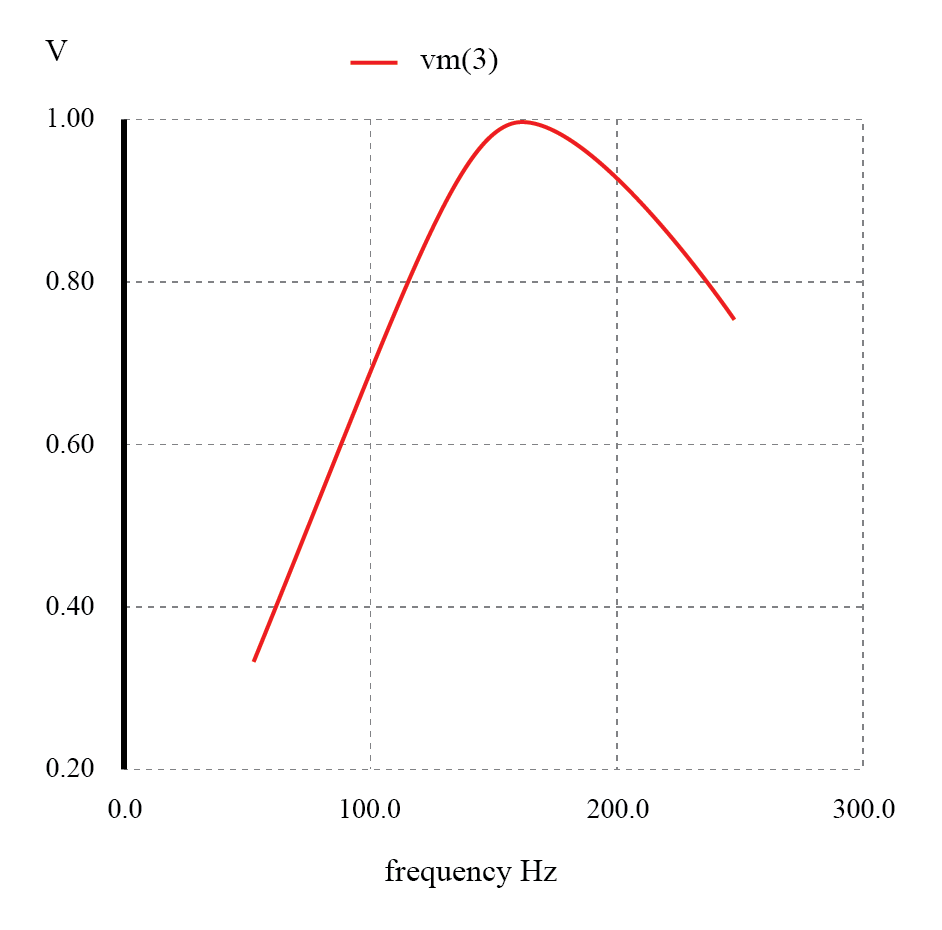
直列共振バンドパスフィルター:159.15Hzの共振周波数で電圧ピーク。
注意すべき点がいくつかあります。コンデンサまたはインダクタのみで作成されたバンドパスフィルタとは異なり、「通過帯域」(負荷電圧のピークに近い周波数範囲)内で信号の減衰が実質的にないことを確認してください。
また、このフィルタは、共振周波数が回路抵抗の影響を受けない直列LC共振の原理で動作するため、負荷抵抗の値がピーク周波数を歪めることはありません。ただし、負荷抵抗の値が異なると ボード線図の「急勾配」(フィルターの「選択性」)を変更します。
共振バンドパスフィルターのもう1つの基本的なスタイルは、タンク回路(並列LCの組み合わせ)を使用して、負荷に到達するまでの周波数が高すぎるまたは低すぎる信号を短絡します。
並列共振バンドパスフィルター
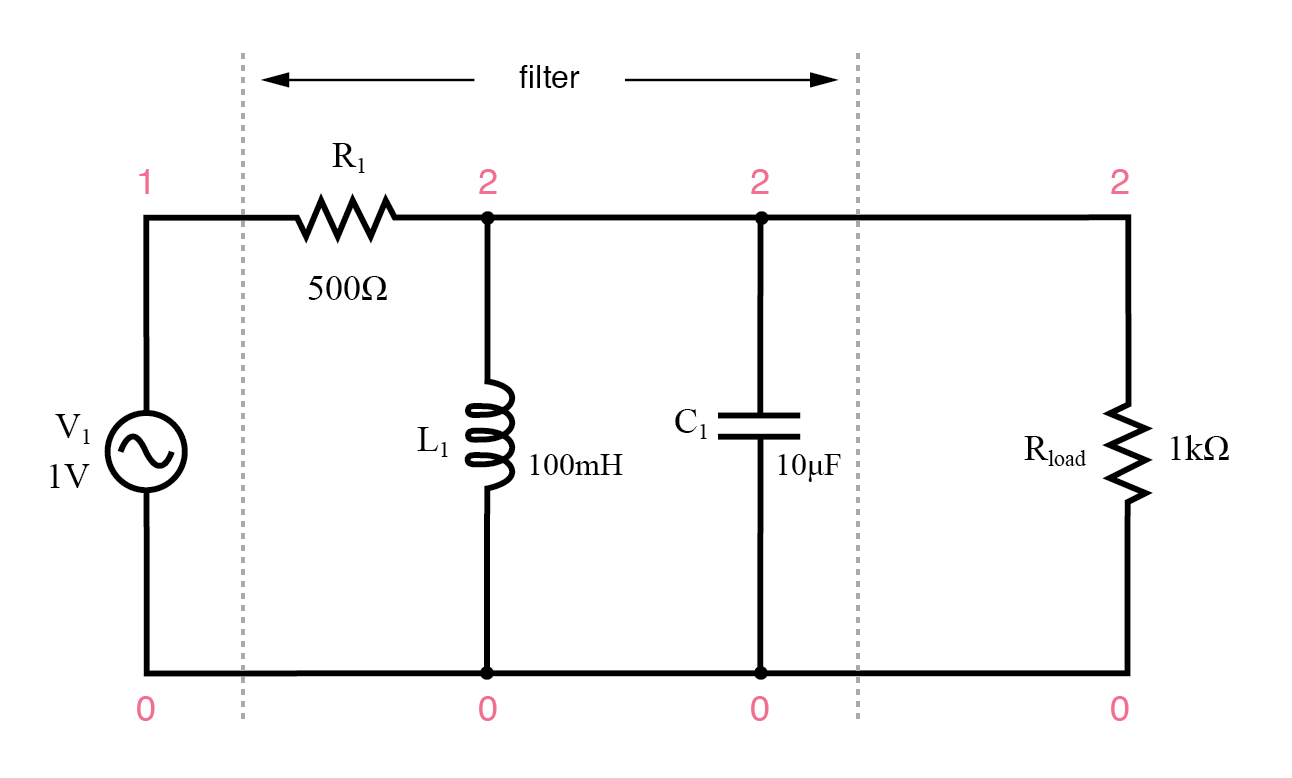
並列共振バンドパスフィルター。
タンク回路は共振時に多くのインピーダンスを持ち、信号が最小限の減衰で負荷に到達できるようにします。ただし、共振周波数が低または過大であると、タンク回路のインピーダンスが低くなり、信号が短絡し、そのほとんどが直列抵抗R 1 にドロップします。 。
並列共振バンドパスフィルター v1 1 0 ac 1 sin r1 1 2 500 l1 2 0100m c1 2 0 10u rload 2 0 1k .ac lin 20 50 250 .plot ac v(2) 。終わり
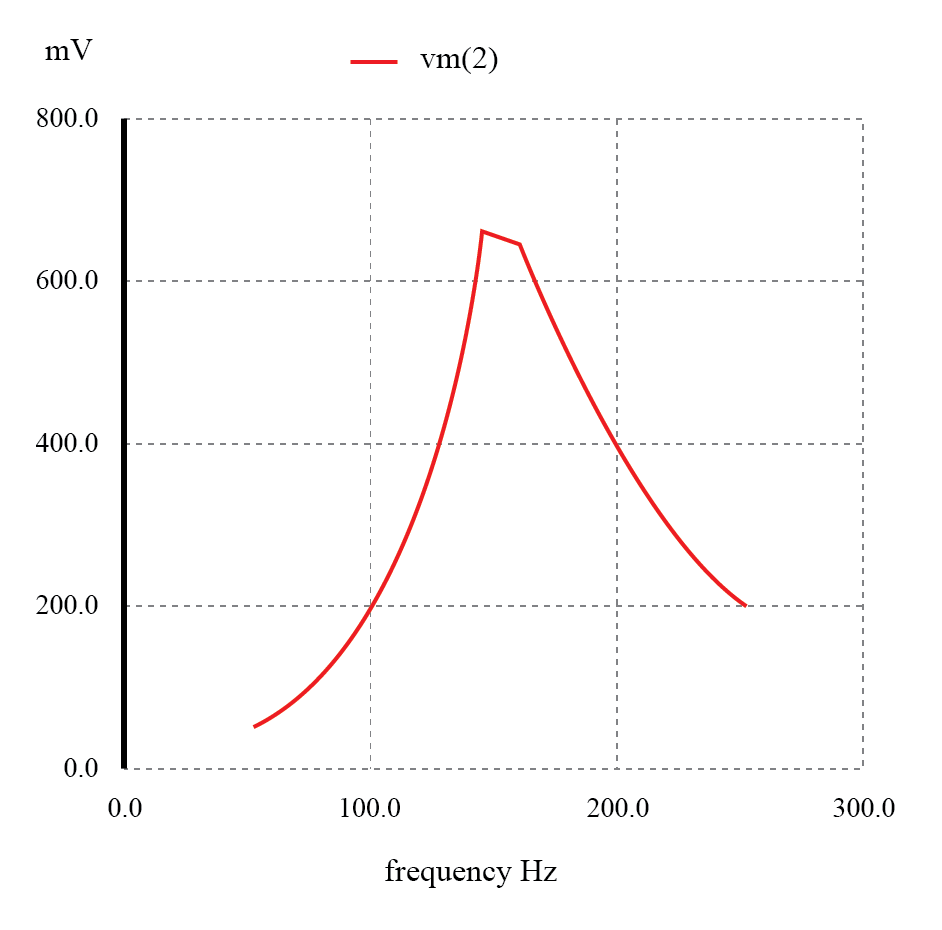
並列共振フィルター:電圧は159.15Hzの共振周波数のピークになります。
不要な周波数を減衰させるために直列抵抗と並列「短絡」コンポーネントに依存するローパスおよびハイパスフィルターの設計と同様に、この共振回路は負荷に完全な入力(ソース)電圧を提供することはできません。
フィルタの出力に負荷抵抗が接続されている限り、その直列抵抗は常にある程度の電圧を低下させます。この形式のバンドパスフィルター回路は、アンテナから利用可能な多数の周波数から特定の無線周波数を選択するために、アナログ無線調整回路で非常に人気があることに注意してください。
ほとんどのアナログラジオチューナー回路では、ステーション選択用の回転ダイヤルがタンク回路内の可変コンデンサーを動かします。

可変コンデンサは、ラジオ受信機のタンク回路を調整して、多くの放送局から1つを選択します。
上の図に示されている単純なラジオの可変コンデンサと空芯インダクタは、あるラジオ局の信号を別のラジオ局の信号と区別するために使用されるタンク回路フィルタの主要な要素で構成されています。
直列および並列LC共振回路を使用して特定の範囲内の周波数のみを通過させることができるのと同様に、それらを使用して特定の範囲内の周波数をブロックし、バンドストップフィルターを作成することもできます。繰り返しになりますが、これを行う際に従うべき2つの主要な戦略があります。それは、直列または並列共振のいずれかを使用することです。まず、シリーズの種類を見ていきます:
シリーズ共振バンドストップフィルター
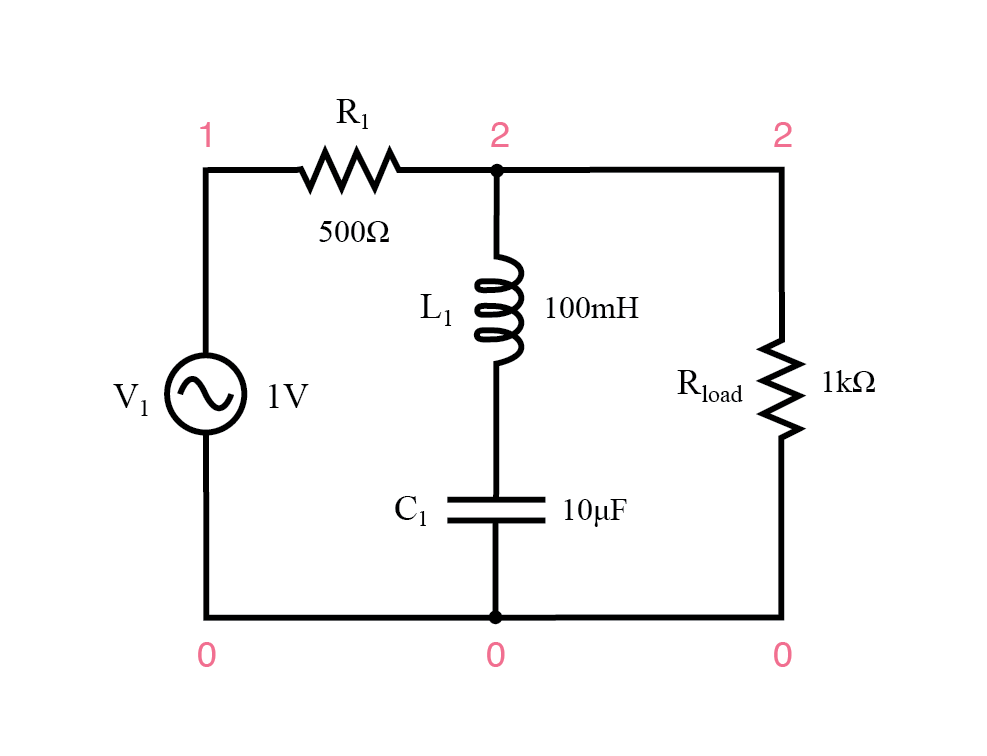
直列共振バンドストップフィルター。
直列LCの組み合わせが共振に達すると、その非常に低いインピーダンスが信号を短絡させ、抵抗R 1 の両端に信号を落とします。 荷物への通過を防ぎます。
直列共振バンドストップフィルター v1 1 0 ac 1 sin r1 1 2 500 l1 2 3 100m c1 3 0 10u rload 2 0 1k .ac lin 20 70 230 .plot ac v(2) 。終わり
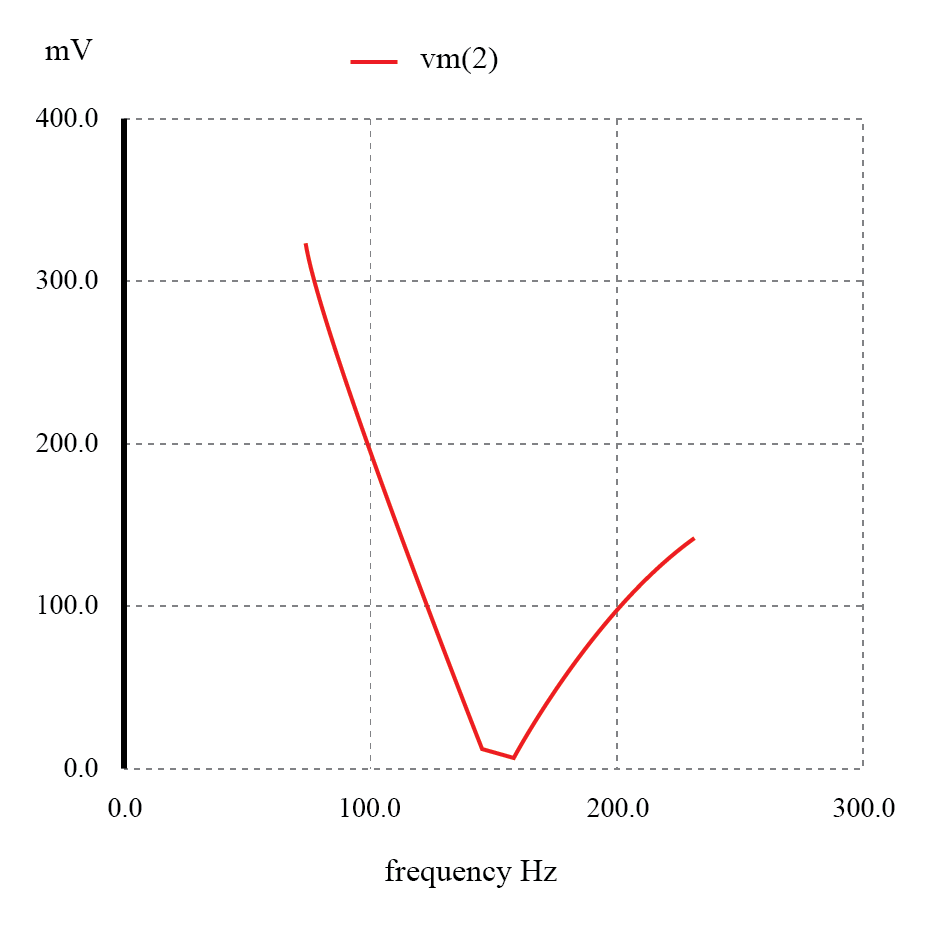
直列共振バンドストップフィルター:ノッチ周波数=LC共振周波数(159.15Hz)。
次に、並列共振バンドストップフィルターを調べます。
並列共振バンドストップフィルター
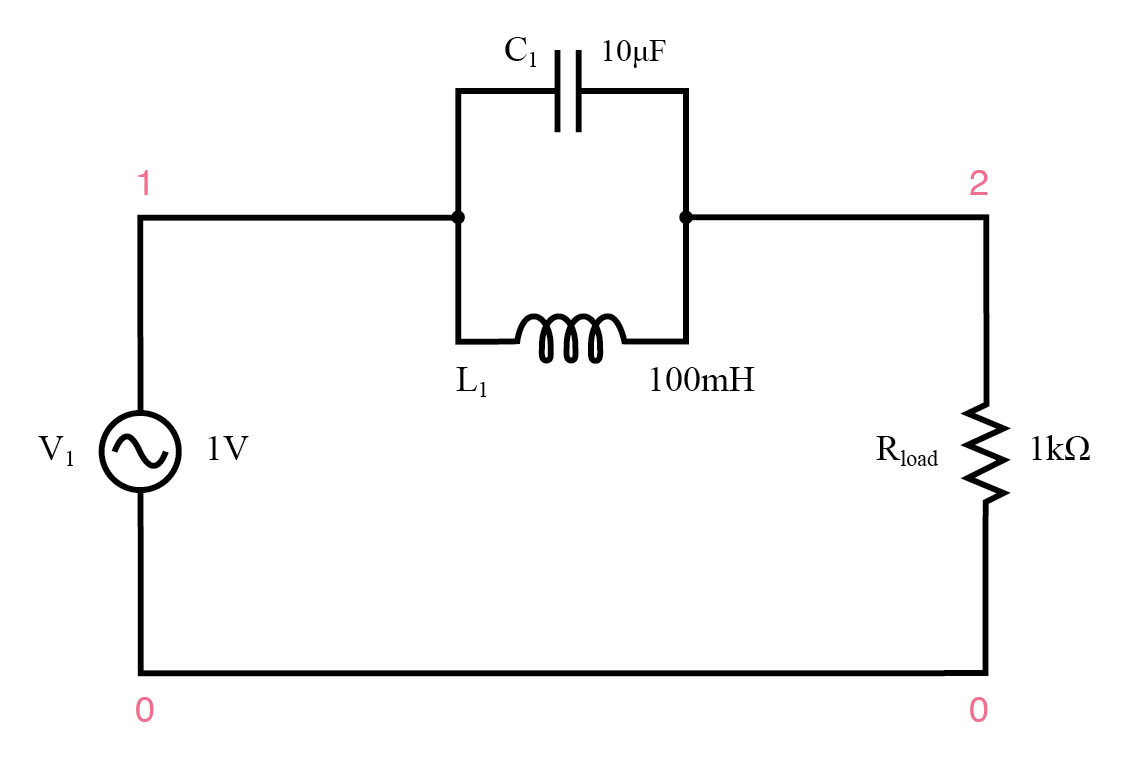
並列共振バンドストップフィルター。
並列LCコンポーネントは、共振周波数で高インピーダンスを示し、それによってその周波数で負荷からの信号をブロックします。逆に、他の周波数で信号を負荷に渡します。
並列共振バンドストップフィルター v1 1 0 ac 1 sin l1 1 2 100m c1 1 2 10u rload 2 0 1k .ac lin 20100200 .plot ac v(2) 。終わり
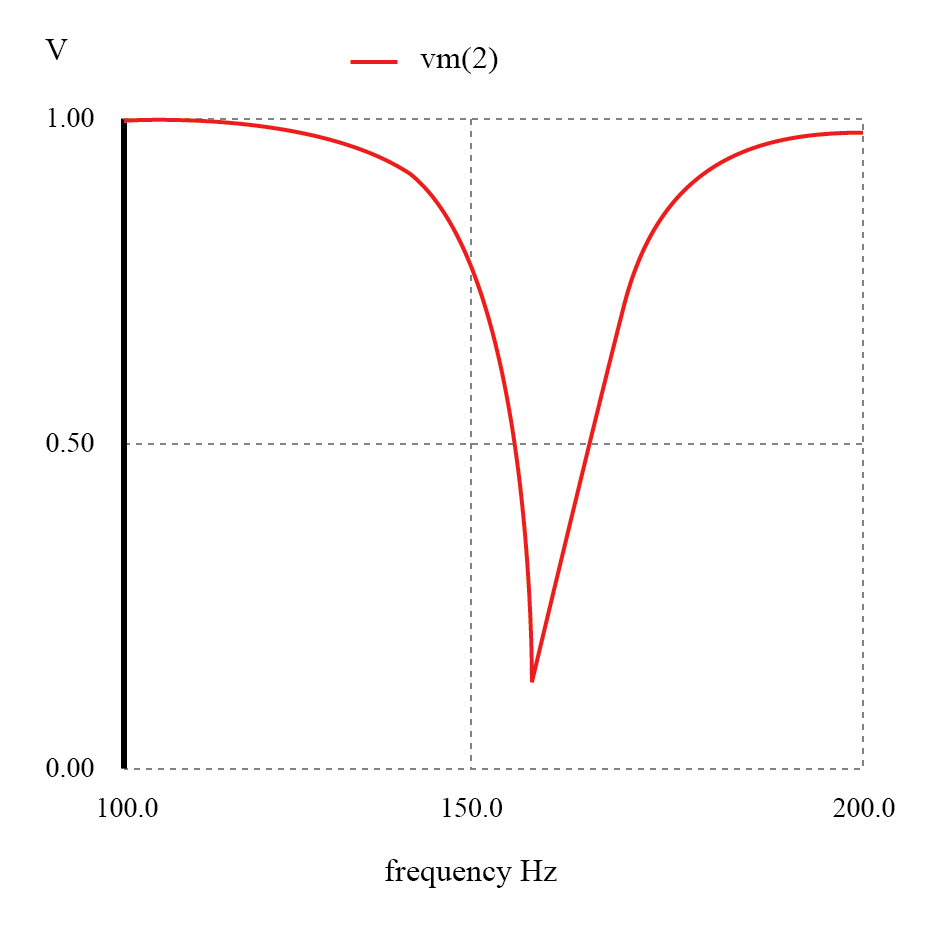
並列共振バンドストップフィルター:ノッチ周波数=LC共振周波数(159.15Hz)。
繰り返しになりますが、直列抵抗がないために、必要なすべての(通過した)信号の減衰が最小になることに注意してください。一方、ノッチ周波数での振幅は非常に小さいです。言い換えれば、これは非常に「選択的な」フィルターです。
これらすべての共振フィルターの設計では、選択性は使用するインダクタンスと静電容量の「純度」に大きく依存します。漂遊抵抗がある場合(特にインダクターにある可能性が高い)、これにより、周波数を細かく区別するフィルターの能力が低下し、ピーク/ノッチ周波数を歪める反共振効果が導入されます。
この時点で、ローパスフィルターとハイパスフィルターを設計する人に注意が必要です。標準のRCおよびLRローパスおよびハイパスフィルターの設計を評価した後、学生は、次のように容量性要素と誘導性要素を組み合わせることで、ローパスまたはハイパスフィルターのより優れたより効果的な設計が実現される可能性があります。下の図。
容量性誘導ローパスフィルター
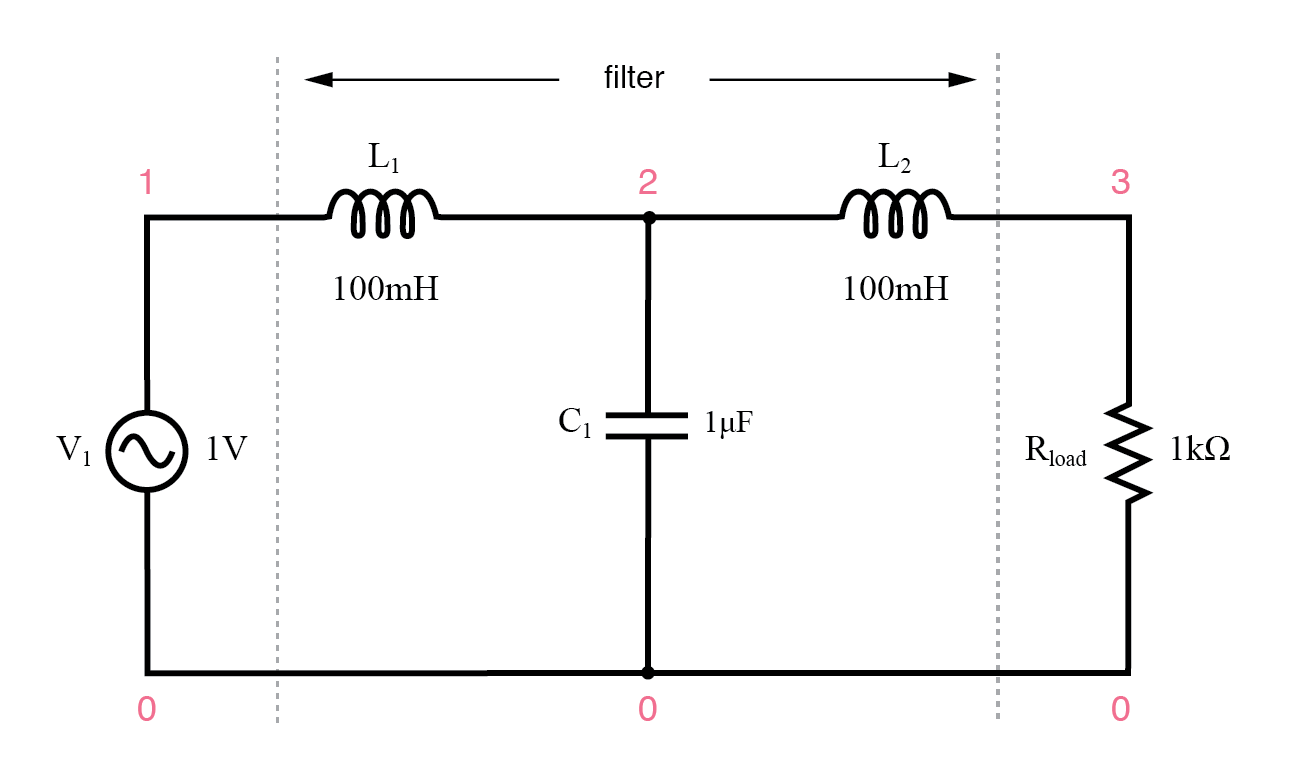
容量性誘導ローパスフィルター。
インダクタはすべての高周波をブロックする必要があり、コンデンサはすべての高周波も短絡する必要があります。両方が連携して、低周波数の信号のみが負荷に到達できるようにします。
最初は、これは良い戦略のようであり、直列抵抗の必要性を排除します。ただし、より洞察力のある学生は、回路内でコンデンサとインダクタを組み合わせると、特定の周波数で共振効果が発生する可能性があることを認識します。
これまで見てきたように、共鳴は奇妙なことを引き起こす可能性があります。 SPICE分析をプロットして、広い周波数範囲で何が起こるかを見てみましょう。
lcローパスフィルター v1 1 0 ac 1 sin l1 1 2 100m c1 2 0 1u l2 2 3 100m rload 3 0 1k .ac lin 20100 1k .plot ac v(3) 。終わり
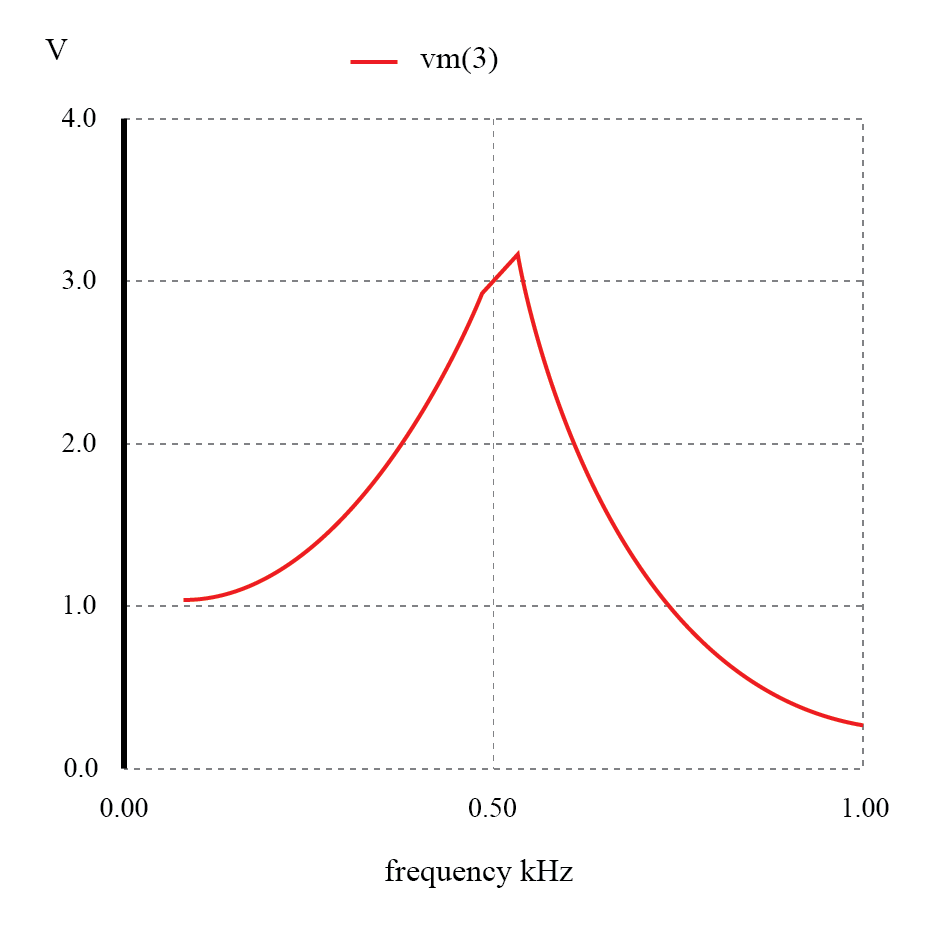
L-Cローパスフィルターの予期しない応答。
ローパスフィルターとされていたものが、526Hz付近にピークを持つバンドパスフィルターであることがわかりました。このフィルタ回路の静電容量とインダクタンスはその時点で共振を達成しており、C 1 付近で大きな電圧降下が発生します。 、L 2 に関係なく、負荷で見られます の減衰の影響。
この時点での負荷への出力電圧は、実際には入力(ソース)電圧を超えています。もう少し考えてみると、L 1 およびC 2 共振していると、AC電源に非常に重い(非常に低いインピーダンスの)負荷がかかりますが、これも適切ではない可能性があります。
同じ分析を再度実行しますが、今回はC 1 をプロットします。 下の図のの電圧vm(2)、およびソース電流I(v1)と、負荷電圧vm(3):
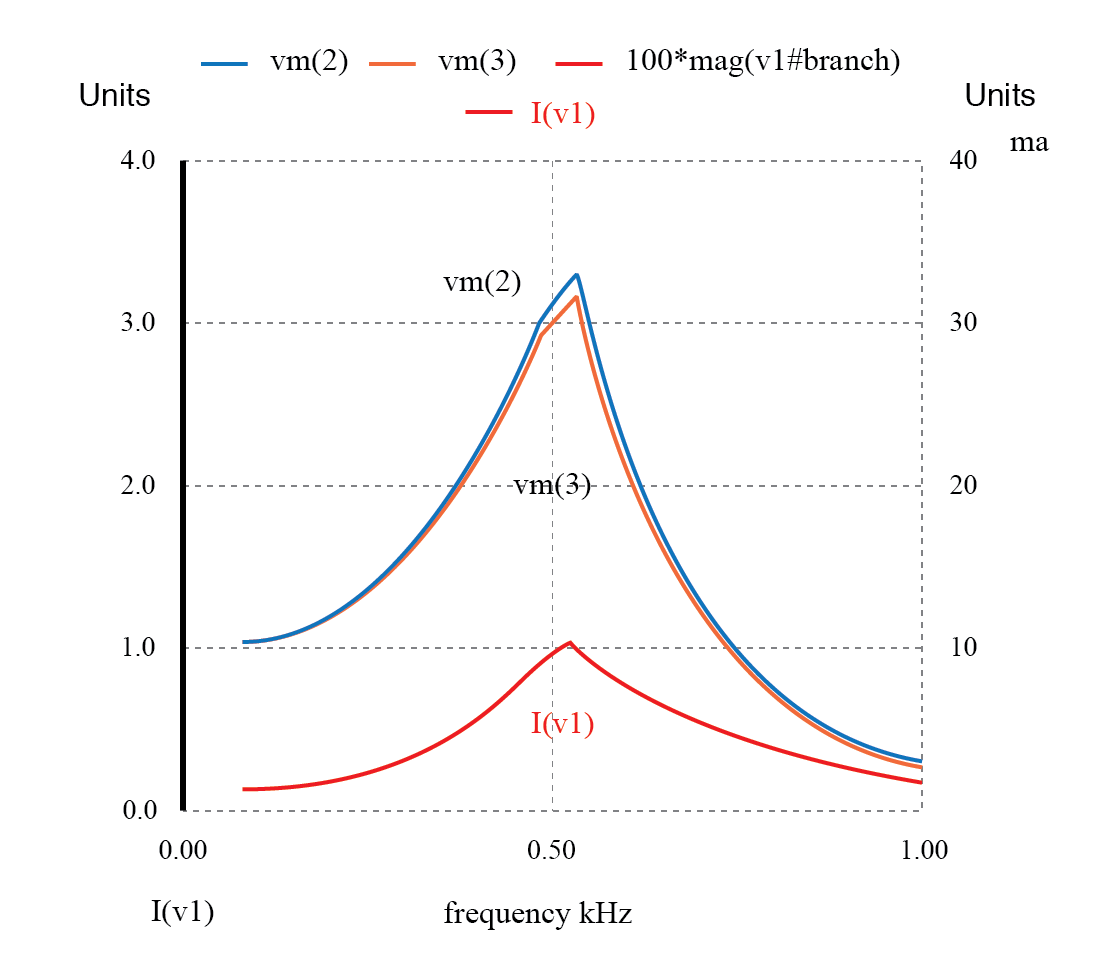
L-Cローパスフィルターの不要な共振で電流が増加します。
案の定、C 1 の両端の電圧がわかります そして、負荷電圧が最大になる同じ周波数で、ソース電流が高いポイントにスパイクします。このフィルターが単純なローパス関数を提供することを期待していた場合、結果に失望する可能性があります。
問題は、L-Cフィルターの入力インピーダンスと出力インピーダンスが一致している必要があることです。電圧源のインピーダンスはフィルターの入力インピーダンスと一致する必要があり、フィルターの出力インピーダンスは「r load 」と一致する必要があります。 」でフラットな応答を実現します。
入力インピーダンスと出力インピーダンスは、(L / C)の平方根で与えられます。
Z =(L / C) 1/2
からコンポーネント値を取得すると、フィルターのインピーダンスと必要なR g を見つけることができます。 およびR load それに合わせて。
L =100 mHの場合、C =1µF Z =(L / C) 1/2 =((100 mH)/(1 µF)) 1/2 =316Ω
下の図では、R g を追加しています。 =316Ωを発電機に接続し、負荷R load を変更しました 1000Ωから316Ωまで。 1000Ωの負荷を駆動する必要がある場合は、その抵抗に一致するようにL / C比を調整できている可能性があることに注意してください。
インピーダンス整合フィルター
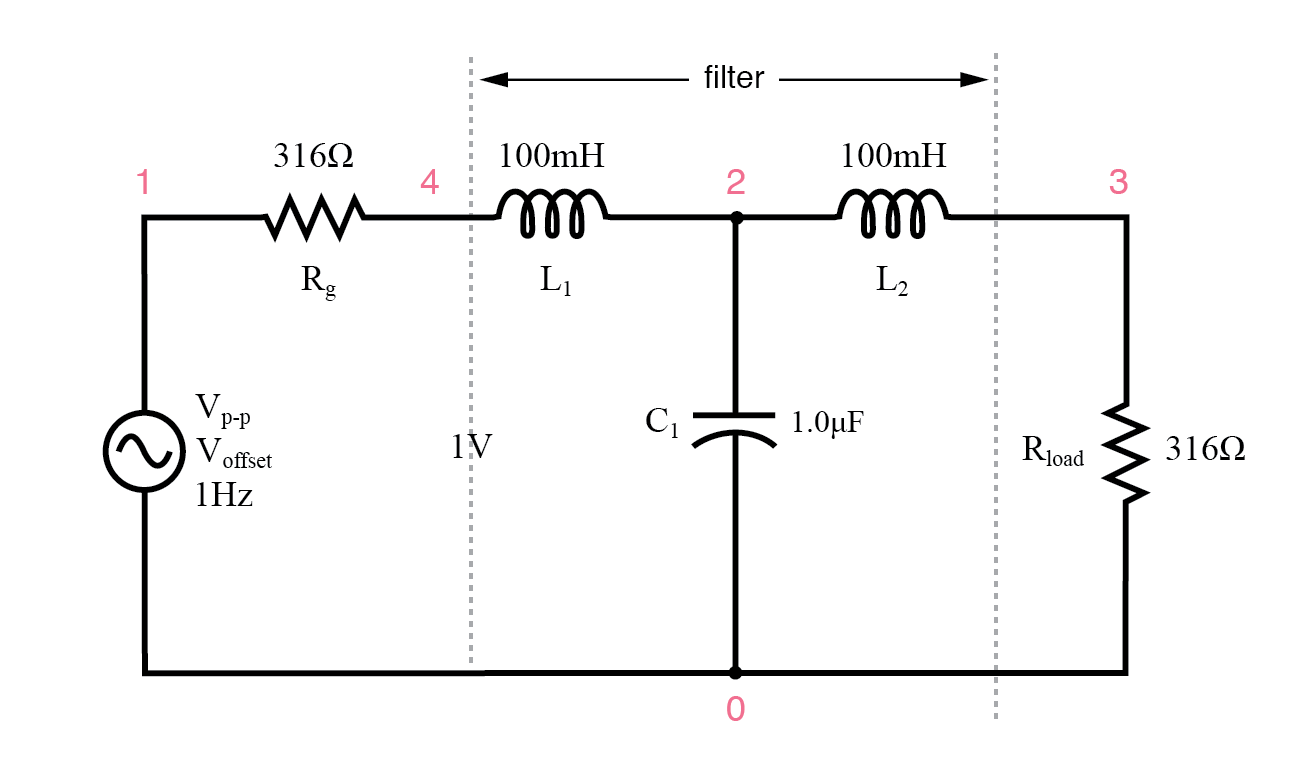
ソースと負荷が一致するL-Cローパスフィルターの回路。
LC整合ローパスフィルター V1 1 0 ac 1 SIN Rg 1 4 316 L1 4 2 100m C1 2 0 1.0u L2 2 3 100m Rload 3 0 316 .ac lin 20100 1k .plot ac v(3) 。終わり
次の図は、ソースと負荷のインピーダンスがフィルターの入力インピーダンスと出力インピーダンスに一致する場合のL-Cローパスフィルターの「フラット」応答を示しています。
インピーダンス整合L-Cローパスフィルターの応答は、カットオフ周波数までほぼフラットです。
整合されていないフィルタの応答を整合されたフィルタと比較する際のポイントは、フィルタの負荷が変動すると電圧が大幅に変化することです。このプロパティは、L-Cフィルター付き電源に直接適用できます– 規制 貧乏です。負荷の変化に伴い、電源電圧が変化します。これは望ましくありません。
この不十分な負荷調整は、スイングチョークによって軽減できます。 。これはチョークです 、インダクタ、飽和するように設計 大きなDC電流が流れるとき。
飽和とは、DC電流が磁気コアに「高すぎる」磁束を生成するため、電流のAC成分が磁束を変化させることができないことを意味します。誘導はdΦ/ dtに比例するため、インダクタンスは大きなDC電流によって減少します。
インダクタンスが減少すると、リアクタンスX L が減少します。 。リアクタンスを減少させると、インダクタ両端の電圧降下が減少します。したがって、フィルタ出力の電圧を上げます。これにより、可変負荷に対する電圧調整が改善されます。
意図しない共振にもかかわらず、コンデンサとインダクタで構成されるローパスフィルタは、ACから変換されたDCから不要なAC「リップル」電圧をフィルタリングするためにAC / DC電源の最終段階として頻繁に使用されます。
この特定のフィルター設計が潜在的に厄介な共振点を持っている場合、これはなぜですか?
その答えは、フィルターコンポーネントのサイズとAC / DCコンバーター(整流器)から遭遇する周波数の選択にあります。 AC / DC電源フィルターで私たちがやろうとしているのは、少量の比較的高周波のAC電圧からDC電圧を分離することです。
フィルタのインダクタとコンデンサは一般に非常に大きく(インダクタには数ヘンリー、コンデンサには数千μFが一般的です)、フィルタの共振周波数は非常に低くなります。もちろん、DCの「周波数」はゼロであるため、LC回路を共振させる方法はありません。
一方、リップル電圧は、変換されたAC電圧の周波数の少なくとも2倍の基本周波数と、それに加えて何倍もの高調波で構成される非正弦波AC電圧です。
60 HzのAC電源(米国では60 Hz、ヨーロッパでは50 Hz)で動作するプラグインザウォール電源の場合、フィルターで検出される最低周波数は120 Hz(ヨーロッパでは100 Hz)であり、これははるかに高い周波数です。その共振点。したがって、そのようなフィルターの潜在的に厄介な共振点は完全に回避されます。
次のSPICE分析では、このようなフィルターの電圧出力(ACおよびDC)を計算します。直列のDCおよびAC(120 Hz)電圧源は、AC / DCコンバーターの混合周波数出力の大まかな概算を提供します。
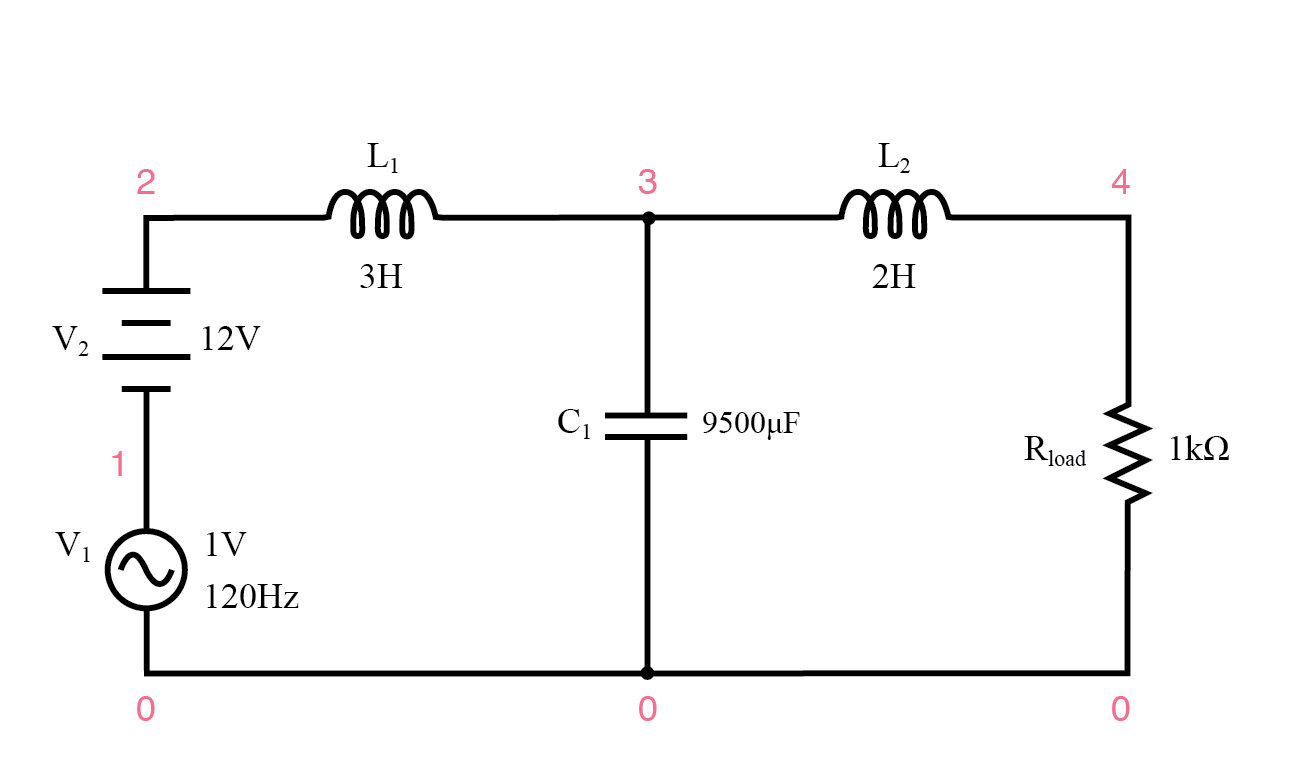
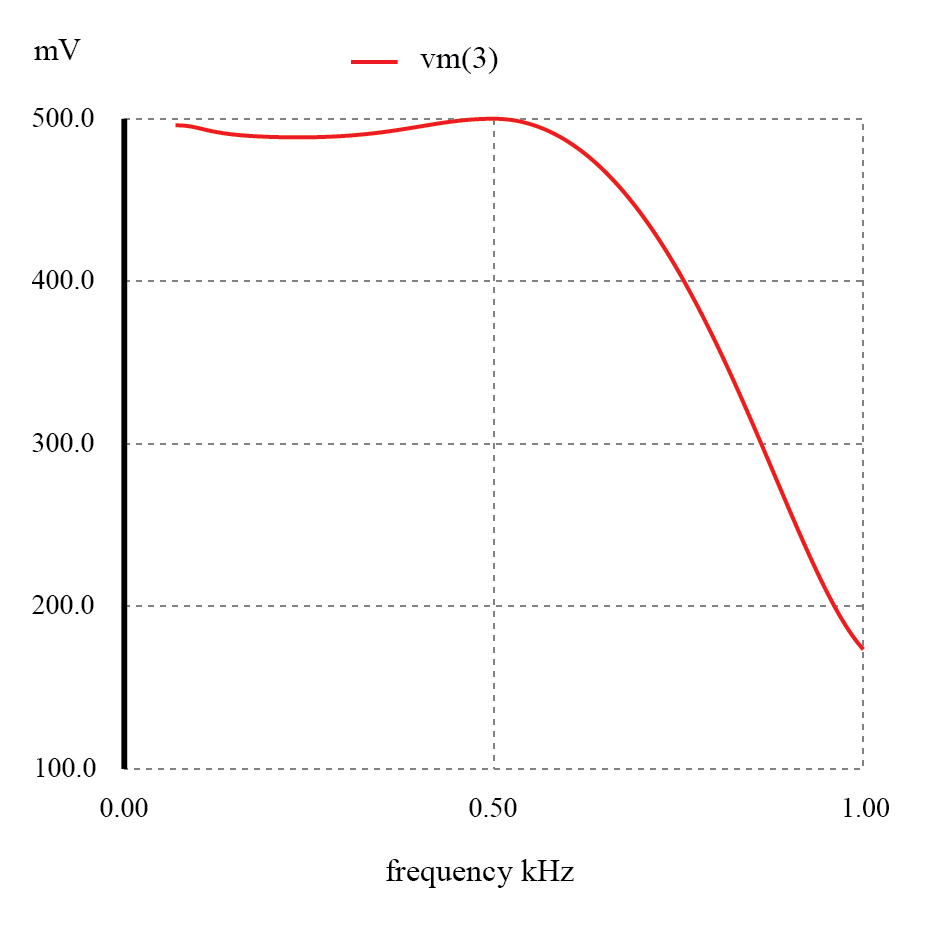
AC / DC電源フィルターは、「リップルのない」DC電源を提供します。
AC / DC電源フィルターは「リップルのない」DC電源を提供します AC / DC電源フィルター v1 1 0 ac 1 sin v2 2 1 dc l1 2 3 3 c1 3 0 9500u l2 3 4 2 rload 4 0 1k .dc v2 12 12 1 .ac lin 1 120 120 .print dc v(4) .print ac v(4) 。終わり v2 v(4) 1.200E + 01 1.200E +01負荷時のDC電圧=12ボルト 周波数v(4) 1.200E + 023.412E-05負荷時のAC電圧=34.12マイクロボルト
負荷に完全な12ボルトのDCがあり、負荷の両端に1ボルトのAC電源からわずか34.12 µVのACが残っているため、この回路設計は非常に効果的な電源フィルターであることが証明されています。
ここで共振効果について学んだ教訓は、コンデンサとインダクタの両方を使用するハイパスフィルタの設計にも当てはまります。望ましい周波数と望ましくない周波数が共振点のいずれかの側に十分にある限り、フィルターは正常に機能します。
しかし、共振周波数に近いかなりの大きさの信号がフィルターの入力に適用されると、奇妙なことが起こります!
レビュー:
- 静電容量とインダクタンスの共振の組み合わせを使用して、回路に抵抗を追加することなく、非常に効果的なバンドパスフィルターとバンドストップフィルターを作成できます。これにより、目的の周波数の通過が減少します。
関連ワークシート:
- レゾナンスワークシート
- パッシブフィルター回路ワークシート
産業技術



