抵抗性および反応性AC回路の電力

120ボルト、60HzのAC電圧源が抵抗性負荷に電力を供給している単相AC電源システムの回路を考えてみましょう:(下の図）

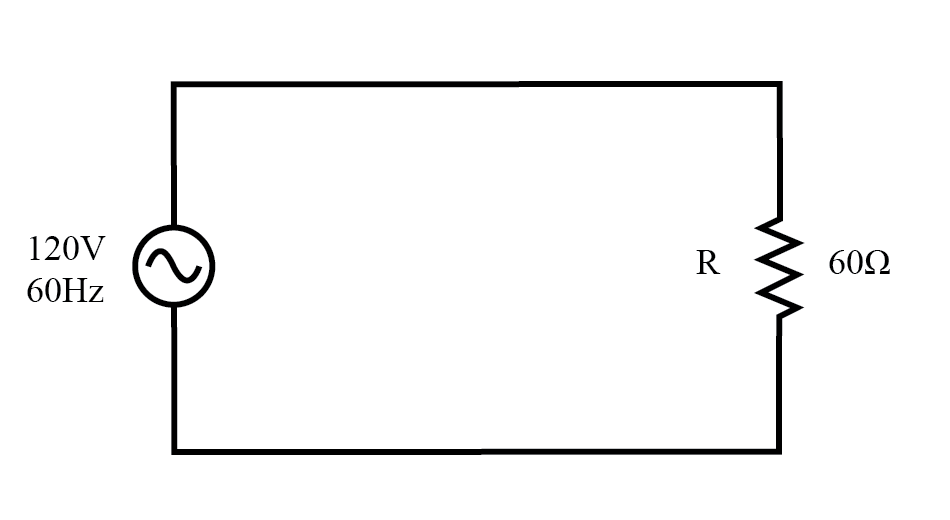
AC電源は純粋な抵抗性負荷を駆動します。

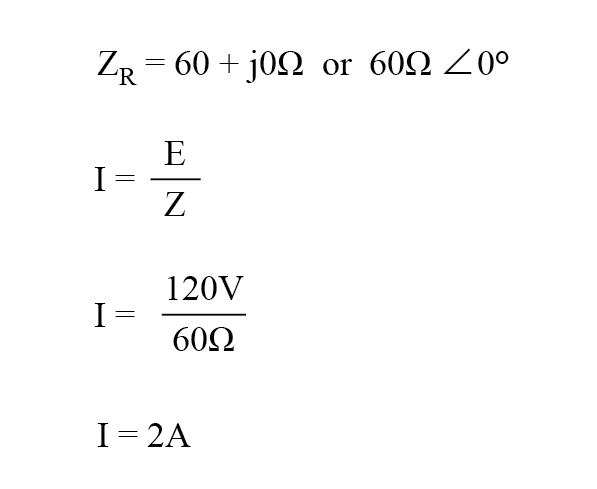
この例では、負荷への電流は2アンペア、RMSになります。負荷で消費される電力は240ワットになります。

この負荷は純粋に抵抗性（リアクタンスなし）であるため、電流は電圧と同相であり、計算は同等のDC回路の場合と同様に見えます。

この回路の電圧、電流、電力の波形をプロットすると、次の図のようになります。

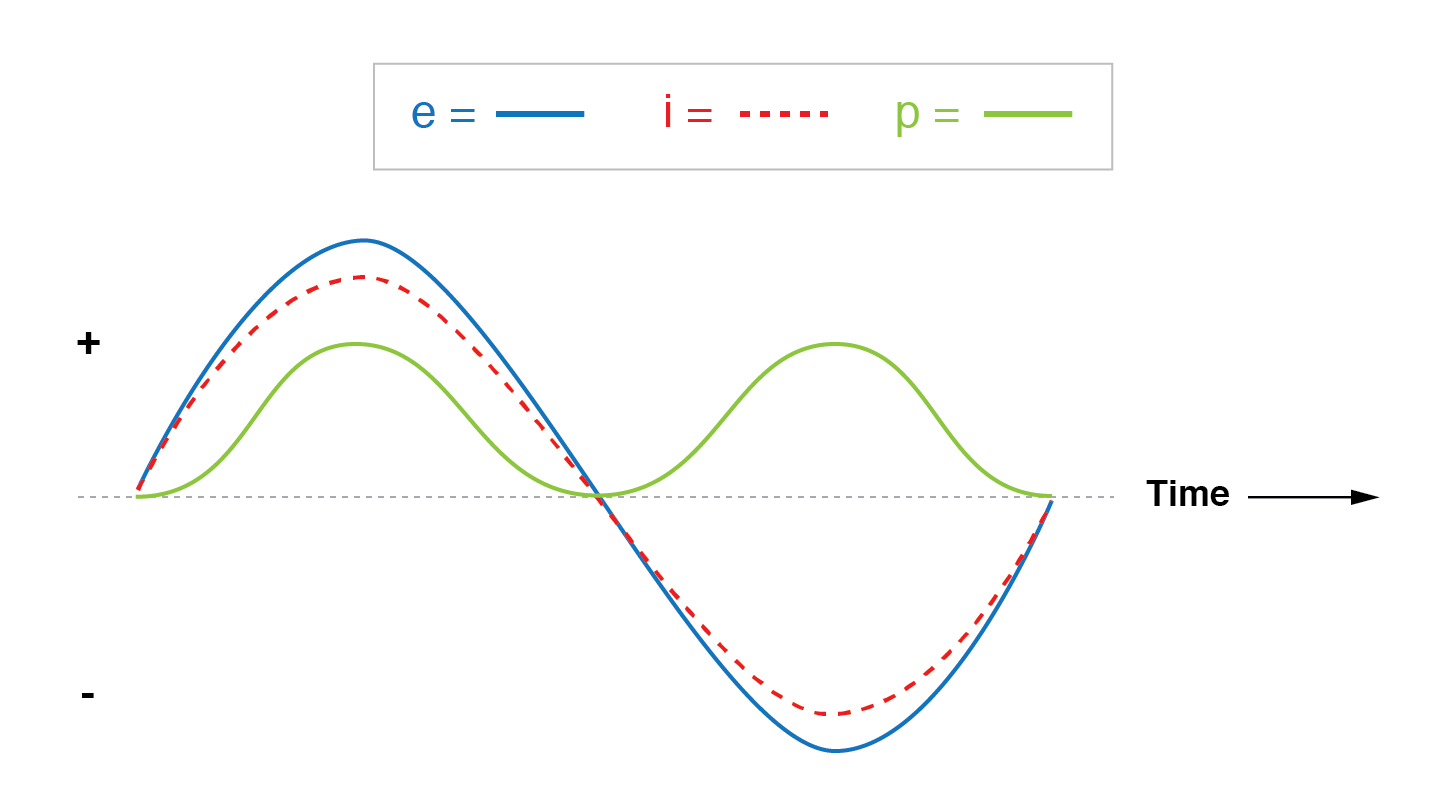
電流は抵抗回路の電圧と同相です。

電力の波形は常に正であり、この抵抗回路では負になることはありません。

これは、電力が常に抵抗性負荷によって消費され、無効負荷の場合のように電源に戻されないことを意味します。ソースが機械式発電機の場合、シャフトを回転させるのに240ワット相当の機械的エネルギー（約1/3馬力）が必要になります。

また、電力の波形は電圧または電流と同じ周波数ではないことに注意してください。むしろ、その頻度は double 電圧または電流波形のいずれかです。

この異なる周波数は、電圧、電流、およびインピーダンスに使用されるのと同じ複素数（長方形または極）表記を使用したAC回路での電力の表現を禁止します。これは、この形式の数学的記号が不変の位相関係を意味するためです。

周波数が同じでない場合、位相関係は常に変化します。

奇妙に思われるかもしれませんが、AC電力の計算を進める最良の方法は、スカラーを使用することです。 表記法と三角法との関連する位相関係を処理します。

純粋に反応性の負荷を備えたAC回路

比較のために、下の図の純粋な無効負荷を持つ単純なAC回路を考えてみましょう。

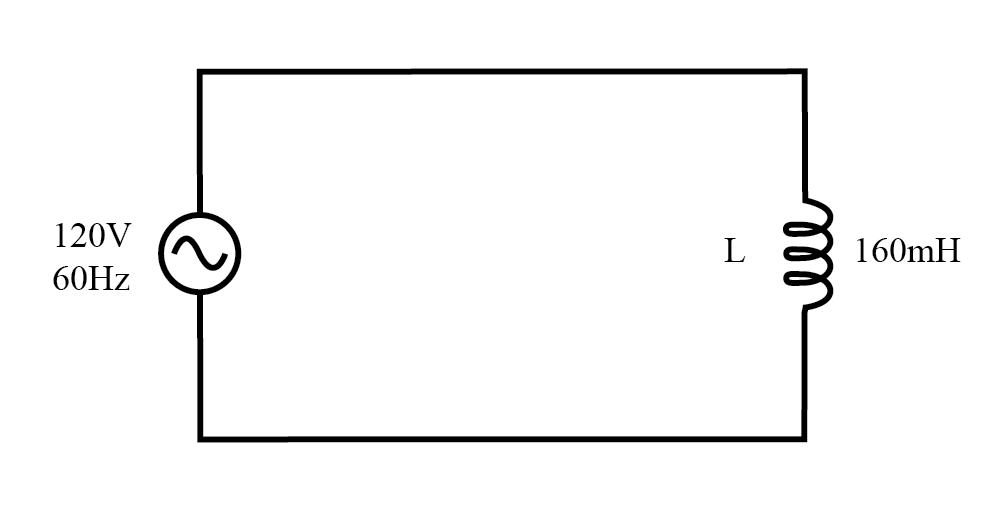
純粋に無効な（誘導性）負荷のあるAC回路。

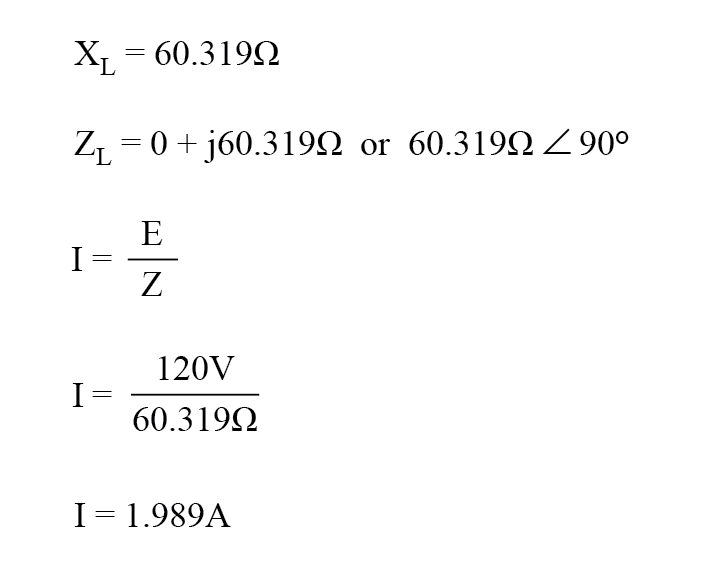
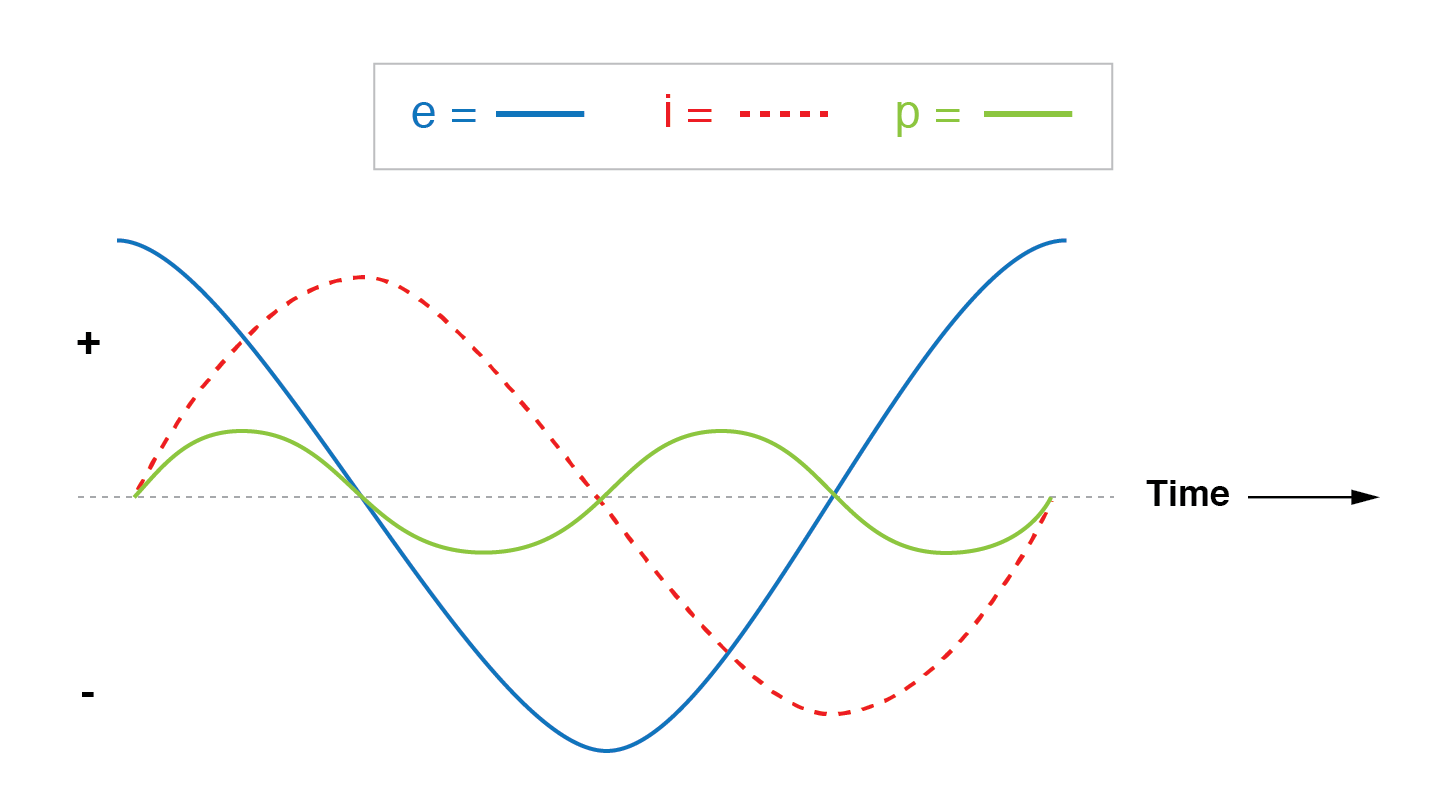
純粋な無効負荷では電力が消費されません。ソースから吸収され、ソースに戻されますが。

電力は、正と負のサイクル間で均等に切り替わることに注意してください。 （上の図）これは、電力が電源から交互に吸収され、電源に戻されることを意味します。

ソースが機械式発電機の場合、負荷によって電力が使用されないため、シャフトを回転させるのに（実際には）正味の機械的エネルギーは必要ありません。

発電機のシャフトは回転しやすく、インダクターは抵抗器のように暖かくなりません。

抵抗性および純粋に反応性の負荷を備えたAC回路

次に、下の図のインダクタンスと抵抗の両方で構成される負荷を持つAC回路について考えてみましょう。

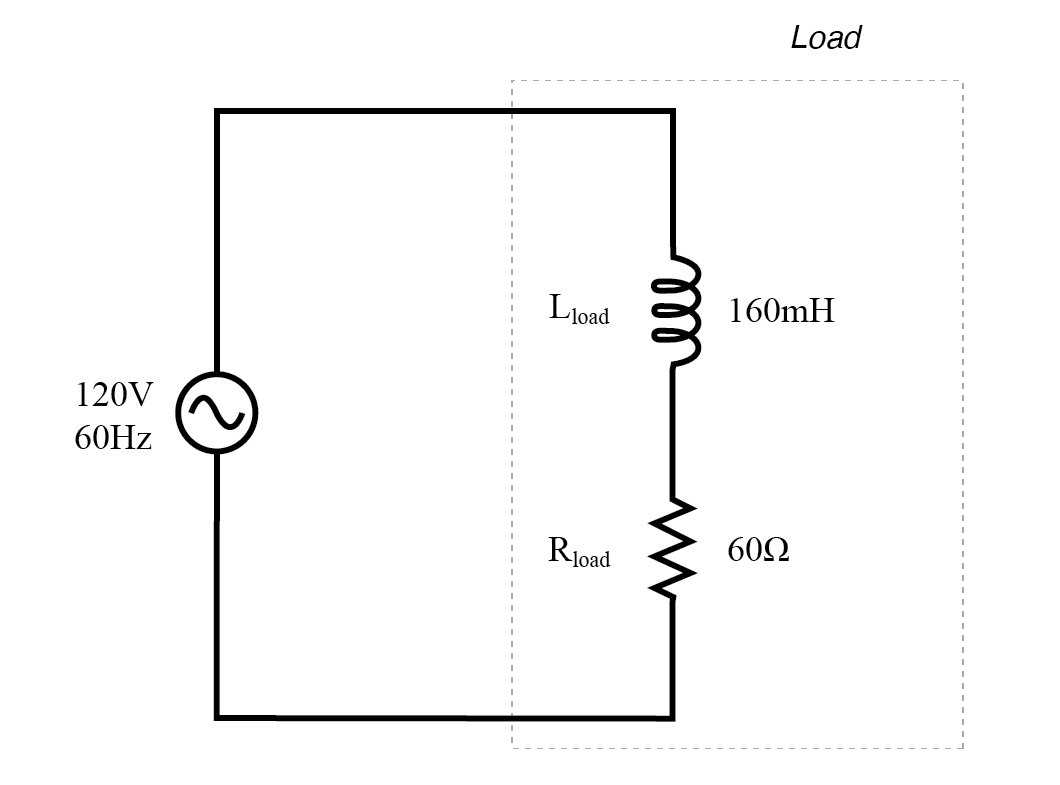
リアクタンスと抵抗の両方を備えたAC回路。

60 Hzの周波数では、160ミリヘンリーのインダクタンスにより60.319Ωの誘導性リアクタンスが得られます。

このリアクタンスは60Ωの抵抗と組み合わされて、60 +j60.319Ωまたは85.078Ω∠45.152 ^o の合計負荷インピーダンスを形成します。 。位相角（現時点では関係ありません）を考慮しない場合は、電圧源の極の大きさ（120ボルト）をインピーダンスの極の大きさで割ることにより、回路の電流を計算できます。 （85.078Ω）。

120ボルトRMSの電源電圧で、負荷電流は1.410アンペアです。これは、RMS電流計が抵抗器およびインダクターと直列に接続されている場合に示す図です。

無効なコンポーネントは、回路の他の部分から電力を均等に吸収し、回路の残りの部分に電力を戻すため、ゼロ電力を消費することはすでにわかっています。

したがって、この負荷の誘導性リアクタンスは、同様にゼロ電力を消費します。

ここで電力を消費するために残されているのは、負荷インピーダンスの抵抗部分だけです。この回路の電圧、電流、および総電力の波形プロットを見ると、この組み合わせが次の図でどのように機能するかがわかります。

抵抗/反応回路を組み合わせると、ソースに戻るよりも多くの電力が消費されます。リアクタンスは電力を消費しません。ただし、抵抗器はそうです。

他の無効回路と同様に、電力は時間の経過とともに正と負の瞬時値の間で切り替わります。

正電力と負電力の交代が均等に分割される純粋な無効回路では、正味の消費電力はゼロになります。ただし、このような抵抗とリアクタンスが混在する回路では、電力波形は正と負の間で交互になりますが、正の電力の量は負の電力の量を超えます。

言い換えると、誘導/抵抗負荷の組み合わせは、ソースに戻るよりも多くの電力を消費します。

電力の波形プロットを見ると、波が中心線の負の側よりも正の側で多くの時間を費やしていることが明らかです。これは、回路に戻されるよりも負荷によって吸収される電力が多いことを示しています。

発生する電力の戻りがほとんどないのは、リアクタンスによるものです。正の電力と負の電力の不均衡は、回路の外部にエネルギーを放散するときの抵抗によるものです（通常は熱の形で）。

ソースが機械式発電機の場合、シャフトを回転させるために必要な機械的エネルギーの量は、正と負のパワーサイクルの間で平均化されたパワーの量になります。

電力波は電圧または電流と同じ周波数ではないため、AC回路の電力を数学的に表すことは困難です。

さらに、電力の位相角は、電圧または電流の位相角とはまったく異なるものを意味します。一方、電圧または電流の角度は、相対的なタイミングのシフトを表します。 2つの波の間で、電力の位相角は比率を表します。 消費電力と戻り電力の間。

このようにAC電力はAC電圧または電流とは異なるため、実際には、スカラーを使用して計算することで電力の数値に到達する方が簡単です。 ベクトルから導出しようとするよりも多くの電圧、電流、抵抗、およびリアクタンス 、または複雑 これまでに取り組んできた電圧、電流、インピーダンスの量。

レビュー：

• 純粋な抵抗回路では、すべての回路電力が抵抗によって消費されます。電圧と電流は互いに同相です。
• 純粋に無効な回路では、負荷によって回路の電力が消費されることはありません。むしろ、電力はAC電源から交互に吸収されてAC電源に戻されます。電圧と電流は互いに90°位相がずれています。
• 抵抗とリアクタンスが混在する回路では、負荷によって消費される電力は返されるよりも多くなりますが、一部の電力は確実に消費され、一部は単に吸収されて返されます。このような回路の電圧と電流は、0°から90°の間の値で位相がずれます。

関連ワークシート：

• AC電源ワークシート