SUPERNODE回路解析|解決された例を使用したステップバイステップ
スーパーノード分析– ステートメント 、数式とステップバイステップの解決例
スーパーノード分析とは何ですか?
今日は、なぜスーパーノード回路分析を使用するのかという一般的な質問に答えようとします。 単純なノードまたはノード回路解析によって回路を単純化できます。 。
前回の記事では、スーパーメッシュ回路解析を使用する理由について説明しました。 回路を単純化するために単純なメッシュ解析を使用する代わりに。この点を理解した場合、これは議論についても同じです。満足できない場合は、次の例で説明してみましょう。
次の図1の両方の回路を検討してください。何か違うことに気づきましたか?
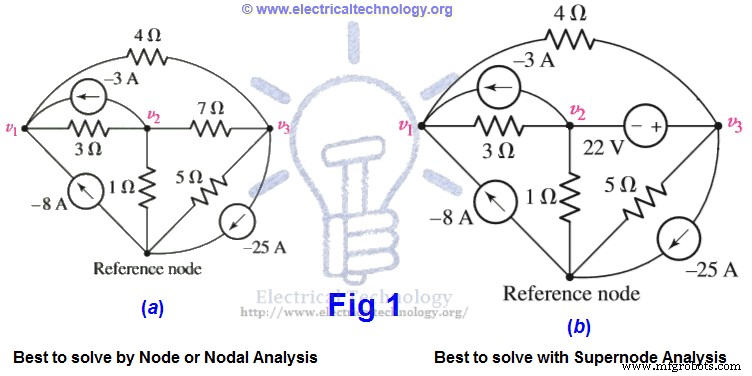
両方の回路の違いは、ノード2とノード3の間の7Ω抵抗の代わりに22Vの追加の電圧源。これが要点です。
ノード またはノード解析 、各非参照ノードにKCL(キルヒホッフの現在の法則)を適用します。つまり、図1(a)の3つのノードに単純なKCLを一度に適用します。
同じことを行う場合、つまり、図1(b)の回路にスーパーノード回路解析の代わりにノード解析を適用すると、ノード1とノード2で問題が発生します。電圧源との分岐の電流は何ですか?さらに、状況を調整するような方法はありません。つまり、電圧を電圧の関数として表すことはできません。電圧源の定義では、電圧は電流に依存しません。これらの困難とトラブルのために、上記の図1(b)では、ノード解析の代わりにスーパーノード回路解析を使用しています。
上記の図1(b)の回路を単純化する方法は2つあります。
最初の st 1つは、より複雑ですが、電圧源を含むブランチに未知の電流値を割り当てることです。次に、3つのノードにKCLを3回適用します(ノードごとに1つのKCL方程式)。最後に、 v であるKVL(キルヒホッフの電圧法則)を適用します。 3 – v 2 =ノード2とノード3の間で22V。この場合、上記の例では未知の値に対して4つの方程式が得られますが、これは単純化するのが少し複雑です。
2番目の この方法は、スーパーノード分析と呼ばれる上記の方法よりも簡単です。この方法では、Node2、Node3、および22Vの電圧源を一緒に一種のスーパーノードとして扱い、KCLを両方のノード(Nod2とNode3)に同時に適用します。
スーパーノードは、点線で囲まれた領域で示されます。これが可能なのは、ノード2を出る合計電流がゼロ(0)で、ノード3を出る合計電流がゼロ(0)の場合、組み合わせを出る合計電流がゼロになるためです。この概念は、スーパーノード(破線で囲まれた領域)とともに次の図2(b)に示されています。
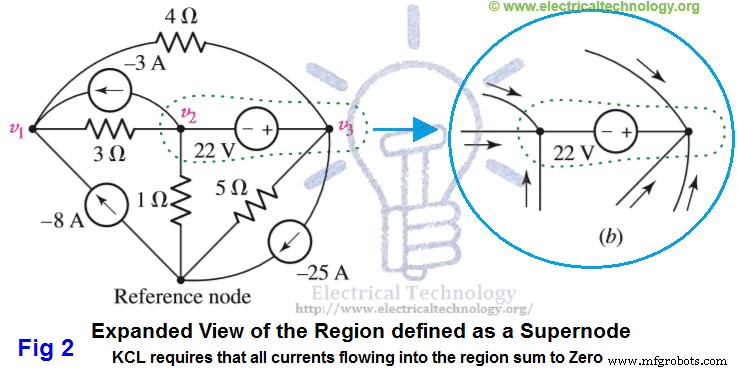
次に、以下の回路を段階的に解きます。スーパーノード回路分析を段階的に行い、次にスーパーノード分析全体を(段階的に)要約します。
- 関連記事:SUPERMESH回路解析|解決された例を使用したステップバイステップ
スーパーノード分析の解決例
例:
スーパーノード分析を使用して、各電流源の両端の電圧を見つけます。つまり、 v 1 & v 2 次の図3(a)?
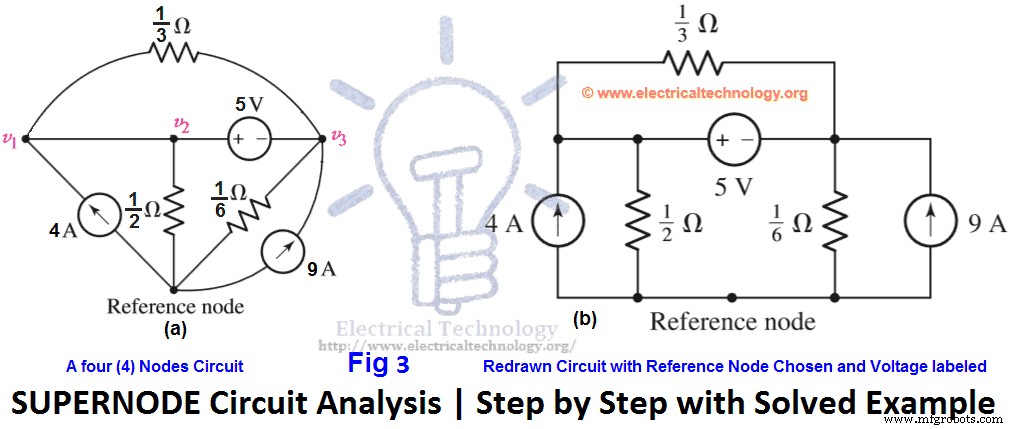
解決策:
まず、図3(b)に示すように回路を再描画します
ノード1のKCL方程式を書くことから始めます。
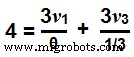
4 =0 + 3 v 1 + 3 v 3 …→式1。
ここで、スーパーノード(Node1とNode2の組み合わせ)について考えてみましょう。さらに、1つの電流源と3つの抵抗が接続されています。したがって、
スーパーノード(ノード1とノード2)にKCLを適用する
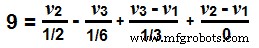
9 =2 v 2 + 6 v 3 + 3 v 3 – 3 v 1 +0。
9 =– 3 v 1 + 2 v 2 + 9 v 3 …→式2。
3つの未知の値があるため、追加の式が1つ必要です。明らかに、ノード2と3の間の5V電圧源を使用します。これは、
v 2 – v 3 =5…→式3。
方程式1、2、3をクラメルの公式またはクラメルの公式計算機で解く 、削除 、ガウスの消去法 またはコンピュータ支援プログラム MATLABなど 、私たちは見つけます、
- v 3 =0.575Vまたは375mV。
- v 2 =5.375V。
- v 1 =1.708V。
スーパーノード分析の概要(ステップバイステップ)
- 回路を再描画します 可能であれば。
- ノードの数を数える サーキットで。
- 参照ノードを設計する 。これは、ブランチの数が最も多いノードである可能性があります。そのため、方程式の数を最小限に抑えることができます。
- ノード電圧にラベルを付ける 。 (N-1)はどれですか 、ここでN=ノードの数。
- スーパーノードを形成する 回路またはネットワークに電圧源が含まれている場合。この作業は、ソース端子と、2つの端子の間に接続されている他の回路要素を点線で囲むことによって行われます。これは上の図2(b)に示されています。
- KCLを作成する (キルヒホッフの現在の法則)各非参照ノードおよび参照ノードを含まない各スーパーノードの方程式。最初の側面では、スーパーノードに流れる電流を追加します または現在のソースからのノード。一方、抵抗を介してスーパーノードまたはノードを出る電流を追加します。 KCL方程式を記述し、回路を解くときは、アカウントの「-」記号を使用してください。
- 定義されたスーパーノードごとに1つのKCL(キルヒホッフの現在の法則)が必要です。これは、KCLを簡単に適用することで実現できます 。簡単に言えば、各電圧源の両端の電圧をノード電圧に関連付けます。
- 依存ソースが回路に表示される場合 、この場合、追加の不明な値を表現します 適切なノード電圧の観点から、ノード電圧以外の電流や電圧などの量。
- 連立方程式を整理して整理する 。
- 最後に、ノード電圧の連立方程式を解きます V 1など 、V 2 、およびV 3 など(N-1、ここで「N」=ノードの数)があります。連立方程式を解くのが難しい場合は、上記の解いた例を参照してください。
- 関連記事:
- テブナンの定理。解決された例を使用したステップバイステップの手順
- ノートンの定理。例を使用した簡単なステップバイステップの手順(図解)
- オームの法則:ステートメントと数式を使用した簡単な説明
- ACおよびDC回路の最大電力伝達定理
- キルヒホッフの電流および電圧法(KCLおよびKVL)|解決した例
- 補償定理–証明、説明、および解決された例
- 置換定理–解決された例を使用したステップバイステップガイド
- ミルマンの定理– ACおよびDC回路の分析–例
- 重ね合わせの原理–解決例を用いた回路解析
- テレゲンの定理–解決された例とMATLABシミュレーション
- 分圧器ルール(VDR)– R、L、C回路の解決例
- 現在の分流の法則(CDR)–ACおよびDC回路の解決例
産業技術



