ネットワーク分析とは何ですか？

一般的に、ネットワーク分析 回路（相互接続されたコンポーネントの「ネットワーク」）を数学的に分析するために使用される構造化された手法です。技術者またはエンジニアは、直列/並列解析技術による単純化に反する複数の電源またはコンポーネント構成を含む回路に遭遇することがよくあります。そのような場合、彼または彼女は他の手段を使用することを余儀なくされます。この章では、このような複雑な回路の分析に役立ついくつかの手法を紹介します。

単純な回路の分析

単純な回路でさえ、直列部分と並列部分に分解することによって分析に逆らうことができる方法を説明するために、この直並列回路から始めてください。

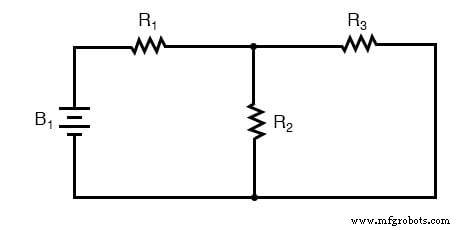
上記の回路を分析するには、最初にR ₂ に相当するものを見つけます。 およびR ₃ 並行して、R ₁ を追加します 直列に接続して、完全な抵抗に到達します。次に、バッテリーB ₁ の電圧を取得します その総回路抵抗を使用して、総電流はオームの法則（I =E / R）を使用して計算でき、次にその電流値を使用して回路の電圧降下を計算できます。全体として、かなり簡単な手順です。

シリーズ/並列解析に逆らう回路

2つのバッテリー回路

ただし、バッテリーを1つ追加するだけで、すべてが変わる可能性があります。

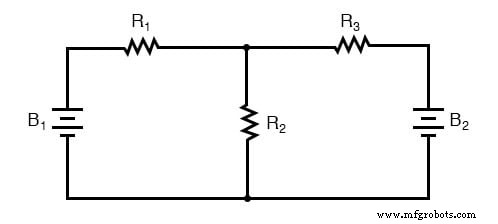
抵抗器R ₂ およびR ₃ B ₂ であるため、互いに並列ではなくなります。 R ₃ に挿入されました の回路の分岐。よく調べてみると、 はないようです。 この回路の2つの抵抗器は、互いに直接直列または並列に接続されています。これが主な問題です。直並列解析では、だった抵抗のセットを特定することから始めました。 直接直列または並列に接続して、単一の等価抵抗に減らします。互いに単純な直列または並列構成の抵抗がない場合、何ができるでしょうか？

抵抗が3つしかないこの一見単純な回路は、単純な直列セクションと単純な並列セクションの組み合わせとして削減することは不可能であることは明らかです。これはまったく異なるものです。ただし、直列/並列解析に反対する回路のタイプはこれだけではありません。

不平衡ブリッジ回路

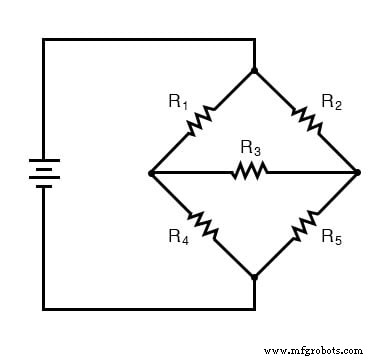
ここにブリッジ回路があります。例として、 ではないと仮定します。 バランス（比率R ₁ / R ₄ 比率R ₂ と等しくない / R ₅ ）。バランスが取れていれば、R ₃ を流れる電流はゼロになります。 、および直列/並列の直並列回路（R ₁ -r ₄ // R ₂ -r ₅ ）。ただし、R ₃ を流れる電流 直列/並列解析が不可能になります。 R ₁ R ₄ と直列ではありません 電流が流れる別の経路があるため、つまりR ₃ 。 R ₂ でもありません R ₅ と直列に 同じ理由で。同様に、R ₁ R ₂ と並列ではありません R ₃ 下部のリード線を分離しています。 R ₄ でもありません R ₅ と並行して 。 Aaarrggghhhh！

この時点では明らかではないかもしれませんが、主な問題は複数の未知の量の存在です。少なくとも直列/並列の組み合わせ回路では、総抵抗と総電圧を見つけて、総電流を単一の未知の値として計算する方法がありました（その後、その電流は、還元プロセスで以前は未知の変数を満たすために使用されました。回路全体を分析できます）。これらの問題があるため、回路の単純化の最も基本的なレベルでは、複数のパラメーター（変数）が不明です。

2つのバッテリー回路では、2つあるため、「総抵抗」の値に到達する方法はありません。 電圧と電流を供給するための電源（ 2つが必要です） オームの法則の計算を進めるための「合計」抵抗）。不平衡ブリッジ回路では、1つのバッテリーの総抵抗（総電流の計算の道を開く）などがありますが、その総電流はブリッジの両端ですぐに未知の比率に分割されるため、それ以上はありません電圧（E =IR）のオームの法則の計算を実行できます。

では、回路内で複数の未知数に直面したときに何ができるでしょうか。答えは、最初は連立方程式として知られる数学的プロセスで見つかります。 または連立方程式 、複数の未知の変数を複数の方程式で相互に関連付けることにより、それらを解きます。未知数が1つしかないシナリオ（これまで扱ってきたすべてのオームの法則の方程式など）では、単一の未知数を解くために必要な方程式は1つだけです。

ただし、複数の未知の値を解く場合、解に到達するには、未知の値と同じ数の方程式が必要です。連立方程式を解く方法はいくつかありますが、すべてかなり威圧的で、この章の説明には複雑すぎます。ただし、多くの科学的でプログラム可能な計算機は、同時に未知数を解くことができるため、これらの回路を分析する方法を最初に学ぶときは、そのような計算機を使用することをお勧めします。

これは最初に思われるほど怖くはありません 。信じて！

後で、これらのタイプの回路で連立方程式を使用する必要をなくすためのトリックを見つけた賢い人がいることがわかります。これらのトリックをネットワーク定理と呼びます。 、およびこの章の後半でいくつか説明します。

レビュー：

• 一部の回路構成（「ネットワーク」）は、複数の未知の値が原因で、直列/並列回路ルールに従って縮小しても解決できません。
• 複数の未知数を解くための数学的手法（「連立方程式」または「システム」と呼ばれる）は、ネットワークを解くための回路の基本法則に適用できます。

関連するワークシート：

• DC分岐電流分析ワークシート
• シリーズ-並列DC回路ワークシート