置換定理–解決された例を使用したステップバイステップガイド
置換定理を使用した電気回路の分析と解決
置換定理
名前が示すように、回路の1つの要素を別の要素に置き換えるために置換定理が使用されます。ただし、エレメントを交換するときは、回路の動作が変わらないように注意する必要があります。
置換定理は次のように述べています;
この定理は、いくつかの定理を証明するために使用されます。ネットワークのブランチを置き換えるために、この定理は境界条件を示します。
電流の値が分岐を通過し、分岐の両端の電圧の値がわかっている場合、この分岐を電圧源、電流源などの他の要素に置き換えることができます。これにより、抵抗器等の値は変化しません。
この定理は、直列または並列に接続された3つ以上のソースを持つ回路には適用できません。
- 関連記事:テブナンの定理。解決例を含むステップバイステップガイド
置換定理の説明
置換定理は、ネットワークの任意のブランチを、異なる要素を持つ同等のブランチに置き換えることです。この定理では、ブランチまたは要素が元のネットワークと同じ電圧および電流源に置き換えられた場合、そのブランチの電圧と電流があります。
下の図に示すネットワークでの置換定理を理解しましょう。
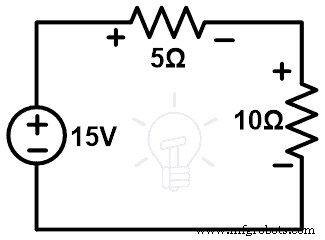
上の図に示すように、DC電源と直列に接続された2つの抵抗があります。次に、ブランチまたは要素を他の要素に置き換えようとします。その前に、すべての分岐を通過する電圧と電流を知る必要があります。
ここでは、この回路にはループが1つだけあります。したがって、電流はすべての分岐を通過し、要素は同じです。この電流は、KVLをネットワークに適用することで決定できます。
たとえば、ループを通過する電流の量です。
+ 15 =5 I +10私
15 =15私
私 =1A
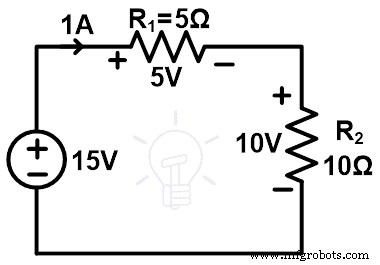
したがって、各要素を流れる電流は1Aです。次に、すべての要素の電圧を見つける必要があります。
1つのブランチに電圧源があります。したがって、その分岐の電圧は見つかりません。この電圧は2つの抵抗に分割されます。そして、各抵抗器の両端の電圧を見つける必要があります。分圧器のルールを適用することで見つけることができます。
つまり、5Ω抵抗の両端の電圧は;
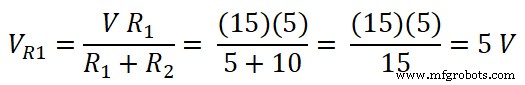
同様に、10Ω抵抗の両端の電圧は;
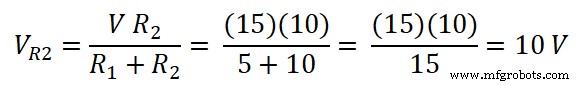
- 関連記事:ノートンの定理。解決例を含むステップバイステップガイド
代替-1
次の図に示すように、10Ωの抵抗ブランチを10Vの電圧源に置き換えることができます。
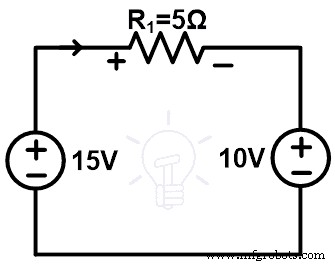
次に、KVLをネットワークに適用します
+ 15 – 10 =5私
5 =5 I
私 =1 A
したがって、ループ電流は元の回路と同じです。次に、要素間の電圧を計算します。 10Ωの抵抗分岐は10Vの電源に置き換えられています。したがって、その分岐の両端の電圧は10Vです。そして、この電圧は元の回路のその分岐の電圧と同じです。
ここで、5Ω抵抗ブランチの両端の電圧を見つけます。この分岐を流れる電流は1Aです。したがって、オームの法則によれば、
V 5Ω =1 A ×5=5 V
したがって、電流はすべてのブランチを通過し、すべてのブランチの電圧は元のネットワークと同じになります。
代替-2
5Ωの抵抗ブランチを削除します。そして、この分岐を5Vの電圧源に置き換えます。この置換の回路図は下図のようになります。
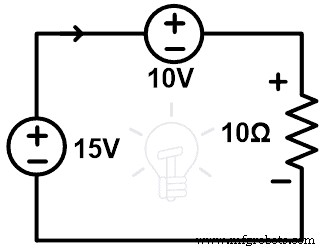
次に、すべてのブランチの電流と電圧を計算し、元のネットワークと比較します。
ループを通過する電流を見つけるには、KVLを適用します;
+ 15 – 5 =10私
10 =10私
私 =1 A
したがって、ループ電流または要素を通過する電流は、元のネットワークを通過する電流と同じです。
5Ω抵抗ブランチは5V電圧源に置き換えられています。したがって、この分岐の電圧は元のネットワークの電圧と同じです。次に、10Ωの抵抗ブランチの両端の電圧を計算する必要があります。
10Ωの抵抗ブランチを流れる電流は1Aです。オームの法則によると;
V 10Ω = IR
V 10Ω =1× 10
V 10Ω =+10 V
したがって、5Ωの抵抗を5Vの電圧源に交換した後でも、ネットワークの動作は変わりません。
- 関連記事:重ね合わせの原理–解決された例を使用した回路解析
代替-3
10Ωの抵抗ブランチを取り外し、1Aの電流源に置き換えます。置換後の回路図は下図のようになります。
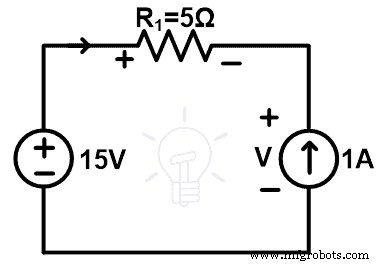
回路に電流源があります。したがって、ループを通過する電流は、電流源の量と同じです。この状態では、1Aの電流源がネットワークに接続されています。したがって、ループを通過する電流は1Aであり、これは元のネットワークを通過する電流と同じです。
次に、5Ωの抵抗と1Aの電流源の両端の電圧を計算します。
オームの法則によると
V 5Ω = IR
V 5Ω =1× 5
V 5Ω =+5 V
ここで、1Aの電流源の両端の電圧を見つけます。 1Aの電流源の両端の電圧をVと仮定しましょう。
上の図から;
+ 15 – 5 – V =0
V =+10 V
したがって、10Ωの抵抗を1Aの電流源に置き換えた後、すべての要素の両端の電圧と電流が元のネットワークと同じであることが証明されました。
- 関連記事:ミルマンの定理– ACおよびDC回路の分析–例
置換-4
10Ω抵抗ブランチを取り外し、5V電圧源と直列に接続された5Ω抵抗に置き換えます。この代替品の回路図は下図のようになります。
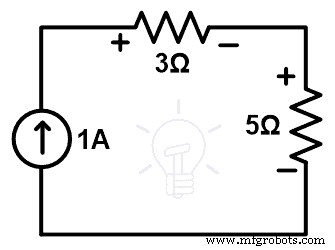
次に、ループを通過する電流を見つける必要があります。したがって、上記のネットワークにKVLを適用します。
15 – 5 =5私 +5私
10 =10私
私 =1A
したがって、要素を通過する電流は元のネットワークと同じです。次に、すべての要素の電圧を見つけます。
5Ω抵抗の両端の電圧を見つけるには;オームの法則を使用します。
V 5Ω = IR
V 5Ω =1×5
V 5Ω =5 V
これで、A点とB点の両端の電圧がわかります。
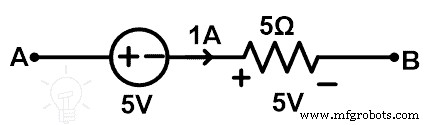
上の図から、5Ω抵抗を流れる電流は1Aです。したがって、この要素の両端の電圧は5Vです。そして、A点とB点の間の合計電圧は
V AB =5 + V 5Ω
V AB =5 + 5
V AB =+10 V
したがって、10Ωの抵抗ブランチを5Ωの抵抗と5Vの電圧源に置き換えた後も、ネットワークの動作は同じままです。
したがって、要素の電圧と電流を変更せずに、また要素の動作を変更せずに、ネットワークの要素の置換を見つけるために利用できるいくつかの方法があると言えます。ネットワーク。
- 関連記事:テレゲンの定理–解決された例とMATLABシミュレーション
置換定理を使用してネットワークを解決する手順
ステップ-1 ネットワークのすべての要素の電圧と電流を見つけます。一般に、電圧と電流は、KCL、KVL、またはオームの法則を使用するだけで計算できます。
ステップ2 電流源、電圧源、抵抗などの別の要素によって削除したい関連するブランチを見つけます。
ステップ3 電圧と電流が変化してはならないという条件で、置換された要素の適切な値を見つけます。
ステップ4 すべての要素の電圧と電流を計算して、新しい回路を確認します。そして、それを元のネットワークと比較します。
これはすべて置換定理に関するものです。それでは、例を見てみましょう。
- 関連記事: ACおよびDC回路の最大電力伝達定理
置換定理の例と解決策
置換定理を使用して以下のネットワークを解き、すべての抵抗器の電流と電圧を計算します。
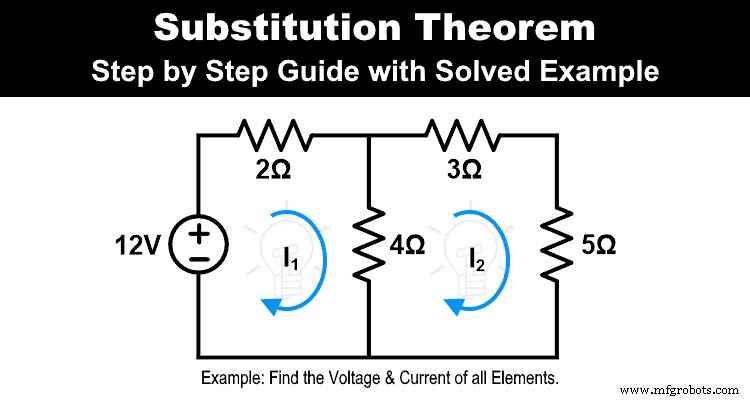
ステップ-1 すべての要素の電圧と電流を見つけます。そのために、この例では、KVLをネットワークに適用します。
ループ1にKVLを適用します;
14 =6私 1 –4私 2 …(1)
ループ2でKVLを適用します;
0 =12 I 2 –4私 1
12 I 2 =4私 1
私 1 =3私 2 …(2)
この値を式-1に入れます;
14 =6(3 I 2 )–4私 2
14 =18私 2 –4私 2
14 =14 I 2
私 2 =1 A
式2から;
私 1 =3 A
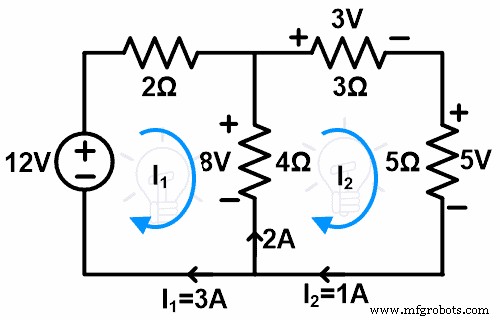
ステップ2 次に、loop-1のブランチを削除して、単一のループを作成します。
ステップ3 4Ω抵抗の代わりに電圧源または電流源を置くことができます。ここに、電流源を入れます。
ループ2を通過する電流は1Aです。したがって、ブランチを1Aの電流源に置き換えます。したがって、残りの回路は次の図のようになります。

ステップ4 すべての要素の電圧と電流を確認しましょう。
このネットワークには単一のループがあります。そして、このループには電流源があります。したがって、ループを通過する電流の値は、電流源の値と同じです。
ここでは、現在のソースの値は1Aです。したがって、電流は3Ωの分岐を通過し、5Ωの抵抗分岐は元のネットワークと同じ1Aになります。
ここで、オームの法則を使用して3Ω抵抗の両端の電圧を見つけます;
V 3Ω = IR
V 3Ω =1 x 3
V 3Ω =3 V
オームの法則を使用して、5Ω抵抗の両端の電圧を見つけます;
V 5Ω = IR
V 5Ω =1 x 5
V 5Ω =5 V
したがって、電圧と電流は元のネットワークと同じです。これが置換定理の仕組みです。
ステップ3で電圧源を選択した場合、電流源の代わりに。この状態では、電圧源の値は4Ωの抵抗分岐の値と同じです。
元のネットワークでは、電流は4Ωの抵抗ブランチを通過します;
私 1 –私 2 =3 – 1 =2 A
オームの法則によると;
V 4Ω =2 x 4 =8 V
したがって、8V電圧源をネットワークに接続する必要があり、残りの回路は次の図のようになります。
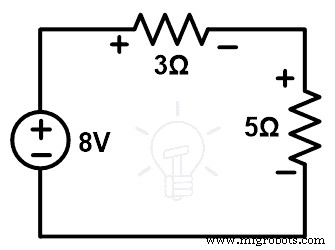
ステップ-4電圧と電流を確認します。上記のループにKVLを適用します。
8 =3私 + 5私
8 =8私
私 =8 A
3Ω抵抗の両端の電圧;
V 3Ω =1× 3 =3 V
5Ω抵抗の両端の電圧;
V 5Ω =1× 5 =5 V
したがって、置換後の電圧と電流は元のネットワークと同じです。
関連する電気回路解析チュートリアル:
- SUPERNODE回路解析–解決された例を使用したステップバイステップ
- SUPERMESH回路解析–解決された例を使用したステップバイステップ
- キルヒホッフの電流および電圧法(KCLおよびKVL)|解決した例
- クラメルの公式計算機–電気回路用の2および3方程式システム
- ホイートストンブリッジ–回路、動作、派生、アプリケーション
- 電気電子工学計算機
- 5000以上の電気電子工学の公式と方程式
産業技術



