磁性ナノ粒子の集合における相互作用効果

背景

磁気温熱療法[1,2,3,4]は、癌治療に関連する現代の生物医学研究において最も有望な方向性の1つです。交番外部磁場で熱を発生させる磁性ナノ粒子の性能は、それらの幾何学的および材料パラメーター、媒体中のナノ粒子の濃度、交番磁場の周波数と振幅などのさまざまな要因の影響を受けます。この論文では、交流磁場上の磁性ナノ粒子の集合体の比吸収率（SAR）に対する相互磁気双極子相互作用の影響を理論的に研究している。酸化鉄のナノ粒子は、生体適合性と生分解性があり、臨床MRIを使用して人体で検出できるため、磁気温熱療法での使用に最も有望であると思われます[2、3、4、5]。この研究では、酸化鉄ナノ粒子に典型的な磁気パラメータを持つナノ粒子の集合体を検討します。最近[4、6]、生物学的環境、たとえば腫瘍に埋め込まれると、磁性ナノ粒子が周囲の組織にしっかりと結合していることがわかりました。したがって、交流外部磁場の影響下での磁性ナノ粒子全体の回転は大きく妨げられます。このような場合、ブラウン運動の緩和は重要ではありません[4]。したがって、交流磁場と熱ゆらぎの影響下での粒子の磁気モーメントの動きのみを考慮する必要があります。さらに、粒子間の磁気双極子相互作用の影響を考慮に入れる必要があります。生物学的媒体中の磁性ナノ粒子は凝集する傾向があり[2、4、7]、フラクタル[8、9]の幾何学的構造を持つナノ粒子の密な凝集体を形成するため、後者の効果は特に重要です。

交流磁場中の磁性ナノ粒子の希薄集合体における熱放散に対する熱ゆらぎの影響は、参考文献で詳細に研究されています。 [10、11、12、13]。特に、そのような集合体のSARは、他の要因の中でも、平均ナノ粒子直径に実質的に依存することが示されている[10]。希薄なナノ粒子アセンブリの場合、詳細な計算[10]により、与えられた粒子の磁気パラメータと、交番磁場の与えられた振幅と周波数でのナノ粒子の最適な直径を決定できます。ナノ粒子の幾何学的および磁気的パラメータを最適に選択することで、1000 kW / kgのオーダーの非常に高いSAR値が予測されています[10、11]。多くの実験で報告されたSAR値[14、15、16、17]が、上記の理論的推定値に非常に近いことは注目に値します。同時に、多くの実験[5、18、19、20、21]で、SAR〜20–50 kW / kgの有意に低い値が測定されました。この事実は、おそらく、磁性ナノ粒子の密集した集合体における強い磁気双極子相互作用の影響によって説明することができます。

実際、磁性ナノ粒子の高密度集合体におけるSARは、本質的に試験サンプルのアスペクト比、つまりサンプルの長さと幅の比に依存することが実験的に示されています[22、23]。これは、交流外部磁場でのナノ粒子の集合体の応答に対する磁気双極子相互作用の影響の間接的な証拠です。磁性ナノ粒子の集合によるエネルギー吸収率に対する磁気双極子相互作用の影響は、最近の多くの理論的および実験的調査で研究されてきました[7、24、25、26、27、28、29、30、31、32 、33、34、35、36、37、38]。ただし、生物学的媒体におけるナノ粒子分布のフラクタル性[8、9]を考慮に入れるには、さらなる調査が必要と思われます。

磁気双極子相互作用の影響を明確に確認するために、この論文では、最初に、相互作用しない酸化鉄ナノ粒子の集合体のSARを計算します。磁気双極子相互作用の効果を研究するために、粒子の磁気モーメントの熱ゆらぎの存在と磁気双極子相互作用の両方を同時に考慮した、ランダウ-リフシッツ確率方程式[13、39、40、41]を数値的に解きます。クラスターのナノ粒子間。 2種類の磁気クラスターが考えられます。剛体媒体に分布するナノ粒子の通常のランダム3Dクラスターと、通常は細胞内空間内に発生するナノ粒子のフラクタルクラスターです。クラスター内では、ナノ粒子は強力な磁気双極子相互作用によって結合されていることに注意してください。同時に、クラスターの希薄なアセンブリの場合、クラスター間の磁気相互作用は、最初の近似では無視できます。

ランダムな3Dクラスターの希薄集合体の特性に対する磁気双極子相互作用の影響は、主にナノ粒子の充填密度ηによって決定されることが示されています。 = N _p V / V _cl 、ここで N _p はクラスター内の粒子の平均数、 V はナノ粒子の体積であり、 V _cl クラスタボリュームです。ヒステリシスループの面積とアセンブリSARは、3Dクラスターの充填密度が調査した充填密度の範囲（0.005≤η）で増加すると、大幅に減少することがわかります。 <0.4。磁性ナノ粒子のフラクタルクラスターの場合、SARの大幅な減少に加えて、通常、最大吸収率はより小さな粒子径にシフトします。フラクタルクラスターのSARは、ナノ粒子表面の非磁性シェルの厚さが増加するにつれて、かなり増加することもわかります。この効果は、磁気温熱療法における磁性ナノ粒子アセンブリの適用に重要である可能性があります。

数値シミュレーション

相互作用しないナノ粒子

交流磁場における相互作用しない超常磁性ナノ粒子の集合体の挙動を最初に思い出させることは有益です。これにより、アセンブリのプロパティに対する磁気双極子相互作用の影響を明確に確認できます。 W.F.によって導出されたフォッカープランク方程式に基づくブラウン[39]、人口数 n の近似運動方程式[10]を得ることができます ₁ （ t ）および n ₂ （ t ）一軸超常磁性ナノ粒子の2つのポテンシャル井戸の

ここで、τ ₁ （ T ）およびτ ₂ （ T ）は、特定の温度での対応する緩和時間です T それぞれ、第1および第2のポテンシャル井戸に対して。緩和時間τ ₁ （ T ）およびτ ₂ （ T ）粒子の容易異方性軸に関して、印加される磁場の振幅と方向に本質的に依存します（参考文献[10]の付録を参照）。反復手順を使用して、ウェルの人口数を計算できます n ₁ （ t ）および n ₂ （ t ）交流磁場のいくつかの期間。交流磁場中で粒子の定常ヒステリシスループを得るだけで十分です。そうするために、磁場方向に沿った減少した粒子磁化の成分の近似関係を使用することができます

ここで、θ ₀ は、粒子の容易異方性軸に対する外部磁場の角度、θです。 _min、1 およびθ _min、2 は、減少した印加磁場の関数としてのポテンシャル井戸の最小値の位置です。 h _e （ t ）= H ₀ sin（ωt ）/ H _a 、ここでω =2π f は角周波数、 H _a 粒子異方性フィールドです。ランダムに配向した独立したナノ粒子のアセンブリのヒステリシスループを取得するには、減少した磁化を平均化する必要があります m _h （ t ）磁場の方向に。近似分析解の精度は、次のようになります。フォッカープランク方程式の（1）、（2）は、相互作用しない磁性ナノ粒子の確率論的ランダウリフシッツ方程式の数値解との直接比較によって検証されています[10]。

ナノ粒子クラスター

交番磁場における相互作用する磁性ナノ粒子の集合体の比吸収率に対する磁気双極子相互作用の影響を調査するために、この論文では、超常磁性ナノ粒子の通常の3Dクラスターの希薄集合体の挙動とフラクタルの挙動を研究します。クラスター[8、9]は、通常、微細な磁性ナノ粒子がロードされた生物学的媒体で発生します。

図1aに概略的に示されているナノ粒子の準球形の3Dクラスターは、その半径 R によって特徴付けることができます。 _cl 、およびナノ粒子の数、 N _p >> 1、そのボリューム内。ナノ粒子の直径はほぼ同じであると想定されています D 、およびそのセンター、{ r _i }、 i =1、2、.. N _p 、はクラスターボリュームにランダムに分散されます。また、粒子が薄い非磁性シェルでコーティングされているため、クラスターの隣接するナノ粒子間の交換相互作用がないと仮定します。前述のように、このような3Dクラスターは、ナノ粒子の充填密度ηによって特徴付けられます。 = N _p V / V _cl 。これは、クラスターのボリュームに分散された磁性材料の総ボリュームです。 D の関係により、クラスターのナノ粒子間の平均距離を定義できます。 _av =（6 V _cl / πN _p ） ^1/3 。次に、ナノ粒子の充填密度はηで与えられます。 =（ D / D _av ） ³ 。

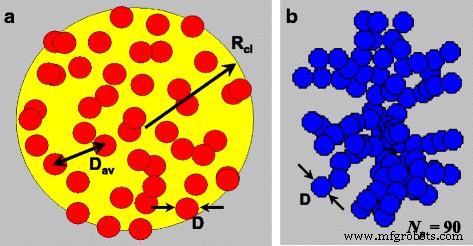
シングルドメインナノ粒子の準球形ランダム3Dクラスターの形状（ a ）およびフラクタルクラスター（ b ）フラクタル記述子 D _f =2.1および k _f =1.3

完全にランダムな3Dクラスターのアセンブリの場合、ナノ粒子の容易な異方性軸の方向{ e _i }、 i =1、2、 .. N _p 、は、単位球上でランダムかつ独立して選択されます。あるいは、静磁気相互作用の影響下での溶液中のクラスターの形成中に、ナノ粒子の容易異方性軸方向の分布に特定の相関関係が生じると仮定することができます。このような半順序クラスターを説明する1つの可能性は、ナノ粒子の容易な異方性軸が立体角θで均一に分布していると仮定することです。 <θ _max 、球面座標で。

与えられた数の粒子を含むランダムな3Dクラスター N _p 直径 D この研究では次のように作成されました。まず、十分に密度が高く、ほぼ均一な N のセットを生成しました。 ランダムポイント{ρ _i }半径 R の球形ボリューム内 _cl 、そのため| ρ _i | ≤ R _cl 生成されたすべてのポイントについて、 i =1、2 ... N 、 N >> N _p 。最初のナノ粒子の中心は、最初のランダムな点 r に配置されました。 ₁ =ρ ₁ 。次に、座標が| ρのすべてのランダムな点 _i – r ₁ | ≤ D ランダムポイントの初期セットから削除されました。この操作の後、ランダムな点の残りのセットの任意の点を2番目のナノ粒子の中心として使用できます。たとえば、単純に r と言うことができます ₂ =ρ ₂ 。次のステップでは、座標が不等式| ρを満たすすべてのランダムな点を削除します。 _i – r ₂ | ≤ D 。この手順は、すべての N まで繰り返されます _p ナノ粒子の中心はクラスターボリューム内に配置されます。その結果、すべてのランダムなナノ粒子の中心は、半径 R の球内にあります。 _cl 、そのため| r _i | ≤ R _cl 、 i =1、2、... N _p 。さらに、どのナノ粒子も隣接するナノ粒子と直接接触していません。このアルゴリズムにより、ナノ粒子の体積分率ηの中程度の値に対して、磁性ナノ粒子のランダムな準球形の3Dクラスターを構築できます。 <0.5。

与えられた初期パラメータのセット、つまり D 、 R _cl 、および N _p 、さまざまなランダム3Dクラスターは、ナノ粒子中心の座標のセットによって異なります{ r _i }と方向{ e _i }粒子の容易な異方性軸。ただし、計算によると、限界 N _p >> 1、確率変数のさまざまな実現のために取得されたヒステリシスループ{ r _i }および{ e _i }は互いにわずかに異なります。ランダムナノ粒子クラスターの希薄なアセンブリの動作を特徴づけるには、十分に多数のランダムクラスターの実現にわたって平均化されたアセンブリヒステリシスループを計算する必要があります。極限で N _p >> 1、クラスターアセンブリの平均化されたヒステリシスループは、初期パラメーター D の固定値を使用して、ランダムクラスターの20〜30の独立した実現にわたって平均化されても、分散がかなり小さくなります。 、 R _cl 、および N _p 。

シングルドメインナノ粒子のフラクタルクラスターの形状は、フラクタル記述子 D によって特徴付けられます[42、43] _f および k _f 。定義上、ナノ粒子の総数 N _p フラクタルクラスターでは、関係\（{N} _p ={k} _f {\ left（2 {R} _g / D \ right）} ^ {D_f} \）で与えられます。ここで、 D > _f はフラクタル次元、 k _f はフラクタルプレファクターであり、 R _g 回転半径です。これは、粒子の中心と骨材の幾何学的な重心との間の距離の平均二乗によって定義されます[43]。この論文では、さまざまなフラクタル記述子を持つフラクタルクラスターが、よく知られているFilippov etal。のアルゴリズムを使用して作成されました[43]。例として、図1bは、フラクタル記述子 D を持つフラクタルクラスターの幾何学的構造を示しています。 _f =2.1および k _f =1.3 N で構成 _p =90個の単一ドメインナノ粒子。幾何学的には、3Dクラスターとフラクタルクラスターの主な違いは、後者の場合、すべてのナノ粒子には、ナノ粒子の直径 D に等しいナノ粒子の中心間の可能な限り近い距離に位置する少なくとも1つの隣接粒子があることです。 。

i の単位磁化ベクトル\（{\ overrightarrow {\ alpha}} _ i \）のダイナミクス -クラスターの1番目の単一ドメインナノ粒子は、確率論的ランダウリフシッツ（LL）方程式によって決定されます

ここで、γ は磁気回転比、κ は現象論的減衰パラメータ、γです。 ₁ =γ /（1+ κ ² ）、\（{\ overrightarrow {H}} _ {ef、i} \）は有効磁場、\（{\ overrightarrow {H}} _ {th、i} \）は熱場です。別のナノ粒子に作用する有効磁場は、全クラスターエネルギーの導関数として計算できます

クラスターの総磁気エネルギー W = W _a + W _Z + W _m は、磁気結晶異方性エネルギー W の合計です。 _a 、ゼーマンエネルギー W _Z 印加磁場中の粒子の割合\（{\ overrightarrow {H}} _ 0 \ sin \ left（\ omega t \ right）\）、および粒子の相互磁気双極子相互作用のエネルギー W > _m 。

一軸タイプの磁気異方性を持つほぼ球形のナノ粒子の場合、結晶磁気異方性エネルギーは次の式で与えられます。

ここで e _i i の容易異方性軸の方向です。 -クラスターの5番目の粒子。ゼーマンエネルギー W _Z 印加磁場中のクラスターの割合は次の式で与えられます

次に、球状の均一に磁化されたナノ粒子の場合、クラスターの静磁エネルギーは、粒子の中心にある点相互作用する双極子のエネルギーとして表すことができます r _i クラスター内。次に、磁気双極子相互作用エネルギーは

ここで n _ij i の中心を結ぶ線に沿った単位ベクトルです -thおよび j それぞれ-番目の粒子。

したがって、 i に作用する有効磁場 -クラスターのn番目のナノ粒子は

ここで H _a =2 K / M _s。 は粒子の異方性場です。

熱場、\（{\ overrightarrow {H}} _ {th、i} \）、 i =1、2 ... N _p 、クラスターのさまざまなナノ粒子に作用することは統計的に独立しており、すべてのナノ粒子の成分の次の統計的特性[39]があります

ここでは、 k _B はボルツマン定数、δです。 _αβ はクローネカーのシンボルであり、δ （ t ）はデルタ関数です。

確率微分方程式を解くための手順。 （3）、（8）、および（9）については、参考文献で詳しく説明されています。 [13、40、41]。

結果と考察

相互作用しない酸化鉄ナノ粒子

平均直径 D の超常磁性ナノ粒子の希薄集合体を考えてみましょう。 。粒子は周囲の媒体に密に詰まっていると想定され、それらの容易な異方性軸は空間内でランダムに配向されます。交流磁場 H におけるそのようなアセンブリのヒステリシスループ = H ₀ sin（ωt ）は、式を使用して計算できます[10]。 （1）と（2）。このアプローチは、その単純さのために、交流磁場の周波数と振幅に応じて、さまざまな粒子サイズのアセンブリヒステリシスループの詳細な計算を実行することができます。実行された計算では、実験データ[2,3,4,5,6]に従って、酸化鉄ナノ粒子の飽和磁化は M であると想定されています。 _s。 =70 Am ² / kg、磁気異方性定数は K =10 ⁴ J / m ³ 。アセンブリ温度は T =300 K、ナノ粒子の直径は D の範囲にあります =10〜30nm。これらのパラメータは、酸化鉄ナノ粒子で実行された実験では典型的なようです。

図2は、一定の振幅の交番磁場 H でのさまざまな周波数での酸化鉄ナノ粒子の非相互作用アセンブリのSARを示しています。 ₀ =8 kA / m。見てわかるように、磁気温熱療法に特徴的な周波数範囲では、 f =200〜500 kHz、SARには、直径 D の酸化鉄ナノ粒子の集合に最大値があります =20〜21nm。交流磁場の比較的中程度の振幅でも、ナノ粒子の直径が適切に選択されていれば、アセンブリSARは350〜450 kW / kgという十分に高い値に達することに注意してください。

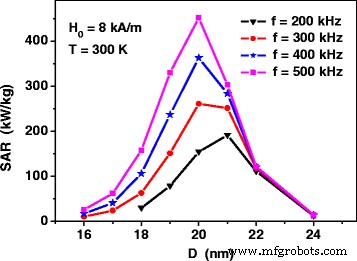
酸化鉄ナノ粒子の非相互作用集合体の比吸収率。 （1）および（2）、交流磁場のさまざまな周波数での平均粒子径の関数として

ただし、酸化鉄ナノ粒子の集合体について実験的に測定されたSAR値は、原則として、これらの理論値を大幅に下回っています[18、19、20、21]。次のセクションで見るように、この事実は[22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]によって説明することができます。磁性ナノ粒子の密集した集合体における強い磁気双極子相互作用の影響。

3Dクラスターのアセンブリ

ここで、空間内でランダムに配向された個々のナノ粒子の異方性軸が容易な3Dランダムクラスターの希薄アセンブリのヒステリシスループについて考えてみます。図2に示すように、相互作用しない酸化鉄ナノ粒子の集合体の場合、交番磁場でのエネルギー吸収のピークは、直径 D の粒子に対応します。 =20nm。したがって、最初に、粒子径 D の3Dクラスターのアセンブリのヒステリシスループを計算しました。 =20nm。

図3aは、ナノ粒子中心間の平均距離 D に応じたアセンブリヒステリシスループの変化を示しています。 _av 粒子径の固定値 D 。交流磁場の周波数と振幅は f に固定されています =400kHzおよび H ₀ =それぞれ8kA / m。クラスター内の粒子の数は N に等しくなります _p =40。計算は T で実行されます =300 K、磁気減衰定数はκと見なされます =0.5。

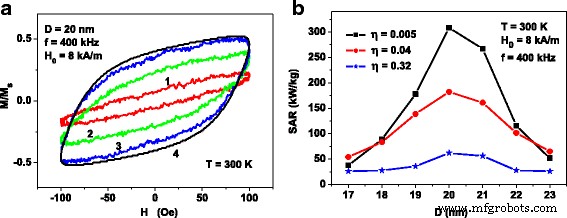
（ a ）直径 D の酸化鉄ナノ粒子のクラスターの希薄集合体のヒステリシスループの進化 =さまざまな比率で20nm D _av / D ：（ 1 ） D _av / D =1.46; （ 2 ） D _av / D =2.92; （ 3 ） D _av / D =5.84。ヒステリシスループ4は、同じ直径の相互作用しないナノ粒子の集合に対応します。これは、式によって計算されます。 （1）と（2）。 （ b ）平均ナノ粒子直径の関数としてのSAR D 異なる充填密度のナノ粒子クラスターの希薄集合体の場合η

明らかに、クラスターのナノ粒子間の平均距離の減少は、クラスター内の磁気双極子相互作用の強度の増加につながります。 N の場合は注意してください _p =40、比率 D _av / D 図3aで指定されているのは、クラスターのパッキング密度ηに対応します。 =それぞれ0.005、0.04、0.32。図3aを見ると、パラメータηの関数としてヒステリシスループ面積が急速に減少していることがわかります。 。比較のために、図3aは、相互作用しない粒子の集合体に対して計算されたヒステリシスループ4も示しています。つまり、限界 D _av / D →∞、 N _p =const、式を使用（1）と（2）。

ヒステリシスループ3（η =0.005）図3aは、相互作用しないナノ粒子の集合体のヒステリシスループに近いことがわかります。したがって、ηの場合 ≤0.005クラスター内のナノ粒子の磁気双極子相互作用は無視できます。ただし、ηの場合 ≥0.04の磁気双極子相互作用は、ランダムな3Dクラスターのアセンブリのプロパティに大きな影響を与えます。周波数 f についても、アセンブリヒステリシスループの同様の進化が得られました。 =それぞれ300kHzと500kHz。

図3aに示すヒステリシスループは、さまざまな比率 D に対して計算されています。 _av / D 、ただし、クラスター内のナノ粒子の数が固定されている場合 N _p =40.ただし、詳細なコンピュータシミュレーションでは、粒子の数が N の場合、ランダムな3Dクラスターの希薄なアセンブリのヒステリシスループの形状は実質的に変化しないことが示されています。 _p >> 1、およびクラスターの半径 R _cl ナノ粒子の充填密度がηになるように変更されます 一定のまま。したがって、ランダム3Dクラスターの希薄アセンブリのヒステリシスループは、主にクラスターのパッキング密度ηに依存します。 。

図3bは、さまざまなηの酸化鉄ナノ粒子のランダムクラスターのアセンブリのSARを示しています。 値。アセンブリのSARは、 SAR として計算されます[10]。 = M _s fA / ρ 、ここで A は変数のヒステリシスループ領域です（ M / M _s。 、 H ）、ρ ρであると想定される酸化鉄ナノ粒子の密度です。 =5×10 ³ kg / m ³ 。図3bに示すように、SARはηの関数として減少します。 クラスター内の磁気双極子相互作用の強度の増加による。同時に、アセンブリSARの平均粒子径への依存性は、あまり目立たなくなりますが、依然として残っています。

ηの値が小さい場合 ≤0.005の場合、3DクラスターのランダムアセンブリのSARは、図2に示すように、相互作用しないナノ粒子のアセンブリのSARと実際に一致します。一方、クラスターのパッキング密度が<まで増加すると、SARは約6倍低下します。 i>η =0.32。次に、酸化鉄ナノ粒子アセンブリを使用した多くの実験[5、18、19、20、21]で得られた一般的なSAR値〜50〜100 kW / kgに近づきます。

フラクタルクラスターのアセンブリ

さまざまなフラクタル記述子を持つナノ粒子のフラクタルクラスターの希薄集合体についても、同様の計算が実行されました。図4に示すように、ナノ粒子のフラクタルクラスターの場合、粒子径の関数としてのSARも、相互作用しないナノ粒子の集合体のSARに比べて大幅に減少します。ただし、3Dクラスターのアセンブリとは対照的に、SARのピーク値は、フラクタル次元 D の場合を除いて、より小さな粒子径に体系的にシフトされます。 _f =2.7、これは D の3Dクラスターの場合に近い _f =3.0。ナノ粒子の直径が最適でない場合、たとえば、直径が D のナノ粒子の場合も興味深いことに注意してください。 ≤17nmの場合、相互作用しないナノ粒子の集合のSARは、直径がi未満のナノ粒子では非常に小さいため、磁気双極子相互作用の影響により、相互作用しないナノ粒子の集合の場合に比べてSARが増加します。> D ≤17nm。

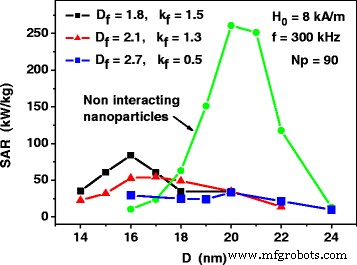
平均ナノ粒子直径の関数としてのSAR D さまざまなフラクタル記述子を持つナノ粒子のフラクタルクラスターの希釈アセンブリ用。非相互作用ナノ粒子の集合体のSARは、式（1）を使用して計算されます。 （1）と（2）

図4に示す計算は、厚さが t の薄い非磁性シェルの存在を想定して実行されました。 _Sh =磁性ナノ粒子の表面で1nm。これにより、フラクタルクラスターのナノ粒子が直接交換相互作用するのを防ぎます。明らかに、ナノ粒子上の磁気コア間の平均距離が増加するにつれて、非磁性シェルの厚さが増加すると、最も近いナノ粒子の磁気双極子相互作用の強度が減少します。図5は、非磁性シェルの厚さを増やすことが、ナノ粒子のフラクタルクラスターのアセンブリのSARを上げる適切な方法であることを示しています。つまり、非磁性シェルの厚さが十分に大きい場合、SARの粒子径への依存性は、弱く相互作用する磁性ナノ粒子の依存性に似ています。この事実は、磁気温熱療法における磁性ナノ粒子アセンブリの適用にとって重要である可能性があります。

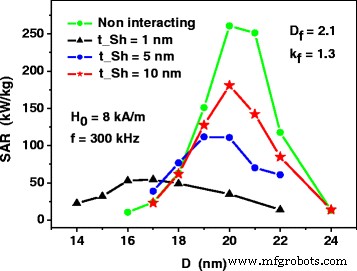
フラクタルクラスターの希薄集合のSARの厚さ t への依存性 _Sh ナノ粒子の表面の非磁性シェルの。非相互作用ナノ粒子の集合体のSARは、式（1）を使用して計算されます。 （1）と（2）

結論

この研究の主な結論は、交流磁場中の磁性ナノ粒子のクラスターの希薄集合体のSARは、クラスター内の磁気双極子相互作用の強度の増加とともに大幅に減少するということです。ナノ粒子の通常の3Dクラスターの場合、磁気双極子相互作用の強度は、無次元のパッキング密度ηによって特徴付けることができます。 = N _p V / V _cl =（ D / D _av ） ³ 。後者は、クラスターのナノ粒子間の平均距離を決定します。計算によると、ランダムな3Dクラスターのアセンブリの場合、エネルギー吸収ピークは、酸化鉄ナノ粒子の場合、平均直径 D の粒子に対応します。 =20 nm、パッキング密度がηから増加すると、約6分の1に減少します =0.005からηまで =0.32。アセンブリSARの平均ナノ粒子直径への依存性は、ηの増加とともに維持されます。 、しかしあまり目立たなくなります。

磁性ナノ粒子のフラクタルクラスターの希薄なアセンブリの場合、アセンブリのフラクタル記述子に関係なく、SAR値も数倍減少します。さらに、SARのピーク値は、原則として、より小さな粒子径に体系的にシフトされます。ただし、ナノ粒子表面での非磁性シェルの厚さの増加により、弱く相互作用するナノ粒子の集合体のSAR値に近いSAR値が復元されることに注意することが重要です。この事実は、磁性ナノ粒子アセンブリのさまざまな生物医学的用途にとって重要になる可能性があります。

この論文で検討されているモデルは、生物学的媒体[4、8、9]（特に腫瘍）で実験的に観察されたナノ粒子集合体の幾何学的構造、つまり、さまざまなサイズの十分に密なフラクタルクラスターにおけるナノ粒子の凝集を考慮に入れています。クラスター内のナノ粒子の数が異なります。確率的LL方程式。 （3）は、粒子間の磁気双極子相互作用と熱ゆらぎの影響の両方を考慮に入れて、ナノ粒子の磁気モーメントの実際のダイナミクスを正確に記述します。研究されたクラスターモデルは、それをより実用的にすることができる明白な一般化を可能にします。まず、アセンブリ内の磁性ナノ粒子のサイズ分布を考慮する必要があります。第二に、場合によっては、クラスターの隣接するナノ粒子が直接原子接触している場合、それらの間に交換相互作用が存在する可能性があります。

この研究で得られた理論的結果は、最適な直径の酸化鉄ナノ粒子に関する最近の実験データ[35]と十分に一致しているようです。確かに、参考文献によると。 [35]、酸化鉄ナノ粒子のSARは、ナノ粒子の平均直径とともに増加し、平均直径 D のナノ粒子のピークになります。 =20〜21nm。さらに、磁気双極子相互作用の強度が増加するため、ナノ粒子間の平均距離が減少すると、SARは減少します[35]。

残念ながら、磁性温熱療法で使用するために磁性ナノ粒子の特性を最適化するために実施されたいくつかの実験的研究[5、21]では、アセンブリSARの特性への有意な依存性に関する理論的予測[10、11]を考慮しないことがよくあります。磁性ナノ粒子のサイズ。この論文に示されているように、この依存性は、かなり高密度のナノ粒子集合体に対してさえもかなりのものになる可能性があります。理論的な観点から、非常に小さい D の酸化鉄ナノ粒子の集合体は明らかです[10]。 ≤10nm、または大きすぎる D 直径が30nm以上の場合、一般的な磁気温熱療法の周波数 f に対して十分に高いSAR値を提供することはほとんどできません。 =200〜600 kHz、磁場振幅 H ₀ 〜8 kA / m。最適な直径に近い鋭いサイズ分布を持つ単結晶酸化鉄ナノ粒子の作成は、磁気温熱療法への応用に有望である必要があります。