最適化された反射率ファセットコーティングによる分散フィードバック量子カスケードレーザーの安定したシングルモード動作

背景

中赤外量子カスケードレーザー（QCL）[1]は、多くの商用アプリケーションにとって最も有望な光源の1つです。ガス検知、自由空間通信、高分解能分光法[2,3,4,5]などのこれらの実用的なアプリケーションには、高出力、改善されたシングルモード信頼性、および低コストのQCLが必要です。その結果、1997年に最初の分散フィードバック（DFB）-QCLが実証されて以来[6]、これらのデバイスの性能は、室温連続波（CW）動作の実証により大幅に改善され、中赤外線領域[7,8,9,10]。ただし、埋め込み格子構造に基づくほとんどのDFB-QCLには、レイジング周波数モードを決定するランダムな劈開ファセットの問題があります。 2つのバンドエッジモードで同じ量の損失があるため、安定したシングルモード動作は保証されません[11]。特に高温条件または大きな注入電流の下で​​は、モードホッピングが常に発生します。これは、これらのシングルモードデバイスのアプリケーションにとって有害で​​す。

安定したシングルモード動作を得るために、レーザーが欠陥モードで動作できるように、回折格子周期に1/4波長位相シフト（λ/ 4PS）が導入されました。したがって、2つのバンドエッジモード間の競合を回避できます。しかし、λ/ 4 PSグレーティングの製造には電子ビームリソグラフィーを使用する必要があり、これには時間と費用がかかります[12]。ゲイン結合DFBレーザーは、従来の半導体レーザーの安定したシングルモード動作を実現するための優れた選択肢です[13]。ただし、エッチングされたアクティブ領域によって大きな損失が発生するため、QCLがゲイン結合DFBレーザーを作成することは非現実的です。もう1つの巧妙な方法は、2つのDFBモード間の差損失を増やすためにキャビティ損失結合メカニズムを使用することです。適切な反射率ファセットコーティングは、高温および大電流でも安定したシングルモード動作を実現できると考えられています。ファセットコーティングに関するいくつかの研究がありますが、それらは常に最適な等価キャビティ長 L の形成に焦点を合わせています。 _opt シングルモードの信頼性ではなく、レーザーのウォールプラグ効率（WPE）を維持するため[14、15]。また、最適化された反射率コーティングは、2つのDFBモード間の競争力を解決するための有望な方法であり、体系的に調査するのに興味深いはずです。

この論文では、λでのDFB-QCLの安定したシングルモード動作 〜4.76μmは、反射防止（AR）/高反射（HR）コーティング後に表示されます。 ARコーティングは、Al ₂ の二重層誘電体で構成されています。 O ₃ （380 nm）およびGe（33 nm）。これらのデバイスは、0.65 kA / cm ² という非常に低いしきい値電流密度を示します。 20°Cで。 26 dBを超えるサイドモード抑制比（SMSR）のシングルモード放射は、モードホッピングなしでCW動作で90°Cの温度まで達成されます。フロントファセットの反射防止コーティングは、キャビティファセットのランダムな位相を抑制するのに非常に価値があると考えられています。

メソッド

理論とシミュレーション

有限DFBキャビティでの反射防止コーティング効果のシミュレーションの中核は、2つのバンドエッジモードのモード損失の計算です。転送行列法は、レーザー構造全体を分析するための適切な方法です[16、17]。この方法を、図1に示すような縦方向の屈折率プロファイルを持つデバイスに適用することを検討します。この概略図は、小さな異なる実効屈折率摂動（ n ）を使用したグレーティングの効果を示しています。 _eff、1 、 n _eff、2 ）およびコーティングされたフィルム（ n ₃ 、 n ₄ ）ガイドモードで。計算に使用した主な材料の複素屈折率は次のとおりです。InP（3.088 + i * 2e-4）、InGaAs（3.4 + i * 2.9e-5）、活性領域（3.298 + i * 4e-5）、高濃度ドープInP（2.81 + i * 1.4e-2）、SiO ₂ （1.3603 + i * 6.3e−4）、Au（1.341 + i * 32.582）、Al ₂ O ₃ （1.5348 + i * 3.2967e−3）、およびGe（4.0165 + i * 4e−2）。次に、さまざまな実効インデックス n _eff、1 =3.1599 + i * 5.17e−5および n _eff、2 =3.1662 + i * 5.6756e-5は、偏微分方程式（PDE）関数を介してCOMSOLで計算されました。レーザーは単一の横モードで動作すると想定されているため、レーザーキャビティに沿った各ポイントでの光の伝搬特性は、単一のスカラー複素量 k で表されます。 、これは媒体の波数ベクトルです。さらに、レーザーは直線偏光であり、それに関連する電場は正弦波の時間依存性を持っていると考えられます e ^{i ω t} 。 上記のこれらの仮定に従って、1次元平面電磁波係数 E _z 波動関数の特殊な変化の部分を表す、はヘルムホルツ方程式を満たします

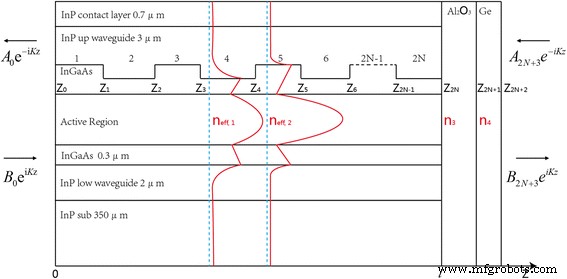
縦方向の光学モードプロファイルに反射防止コーティングを施した有限DFBキャビティのモデルを示す概略図

K （z）は

ここでω および c それぞれ角周波数と光速、そして n （z）は、レーザーキャビティに沿った各ポイントでの複素屈折率です。波数ベクトル k 解決する必要があるのは、次の2つの部分に分けることができます。 k _r および k _i 。実数部 k _r 虚数部 k がレーザーキャビティ内の光の波長を決定しますが、 _i 有限キャビティのモード損失が減衰の原因であることに起因します。図1から、レーザーは2 N のマルチセクションデバイスと見なすことができます。 + N の2つのセクション はグレーティング周期です。これらの各セクションでは、電界 E _n （z）は、2つの逆伝播する指数平面波の線形結合であり、1つは複素振幅で減少しています A _n もう1つは B で増加しています _n 。方程式は次のように記述されます：

合計で2 N + があります 3つのインターフェース。これらの各インターフェースでは、電界と伝搬方向に関するその導関数の両方が、インターフェースの両側で等しくなければなりません。方程式は次のように得られます：

伝達行列 M （ d _n ）によって与えられます

電動ポンピングレーザーが自励発振装置であることを考えると、装置の外部からの到来波はありません。これにより、境界条件 B が発生します。 ₀ = A _{2 N + 3} =0、方程式は次のようになります

波数ベクトル k の各値 式を介してMatlabの助けを借りて取得することができます。 （6）。虚数部 k _i キャビティモードの損失に対応することは、ARコーティング効果の分析に役立ちます。

図2aは、伝達行列シミュレーションに基づく計算結果を示しています。 2つの赤い曲線が示すように、高周波モードの損失は反射率の低下に伴って非常にゆっくりと変化しますが、低周波モードは急激に増加します。挿入図は、グレーティングの単一周期について、低周波数モードと高周波数モードで計算されたモードプロファイルを示しています。プロットされているように、低周波モードは、格子の高屈折率部分である格子ピークでより高い電界の大きさを有し、また、高周波モードは、格子の低屈折率部分により集中している。ファセット反射率のない無限キャビティモデルの場合、高周波モードは常に低周波モードよりもモード損失が低くなります。エンドファセットミラーの影響を無視できれば、導波路損失が小さい高周波モードは常に低下します。ただし、エンドファセットミラーの存在は、レーザーキャビティ内のDFBモードを建設的または破壊的に妨害する反射をもたらします。この干渉は、各モードの有限グレーティングキャビティ損失に影響を与え、どのモードのレーザー発振を決定することができます。ミラーの効果は、両方のミラーの位置が一方のDFBモードの電界振幅のピークと一致する場合に最大になることに注意してください。これは、ミラーがもう一方のDFBモードのノードにある場合でもあります。ここで、コーティングされていないファセットのミラーは低周波モードのピークと一致し、エンドミラーからの反射はレーザーキャビティに存在するモードと最大限に建設的に干渉します。これにより、ミラーの建設的な寄与により、合計モード損失が減少します。反射率が低下し、二重層ARコーティングを使用することで追加の位相シフトの影響を受けると、低周波モードの損失は、干渉効果の弱化とミラー損失の増加による反射率の低下とともに徐々に増加しました。一方、高周波モードの損失は、干渉効果の強化により少し変化しました。これにより、特に前面ファセットの反射率が<0.15の場合、Δモード損失は指数関数と同様に機能します。シミュレーションによると、フロントファセットの反射率が<0.11の場合、スペクトル全体に最小点が1つだけ存在します。これは、別のバンドエッジモード損失が高すぎてレーザー発振できないため、理論的にはモードホップが発生しないことを意味します。

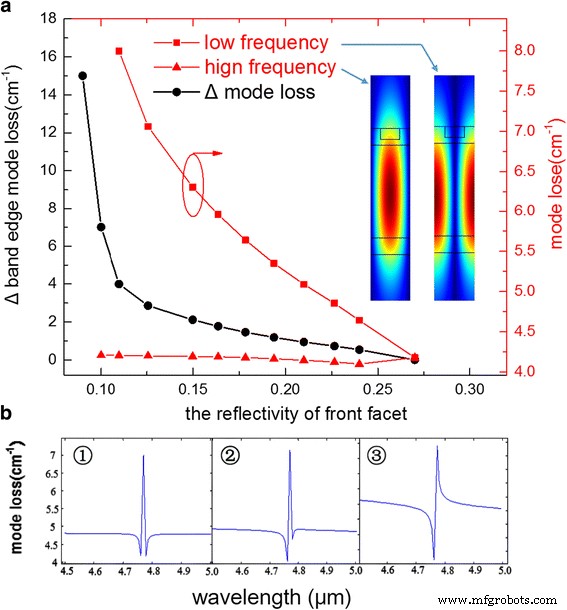
a 2つの赤い曲線は、それぞれ高周波数モードと低周波数モードのモード損失です。黒い曲線は、Δとラベル付けされた2つのバンドエッジモード間の差動モード損失です。挿入図は、グレーティングの単一周期について、低周波数モードと高周波数モードで計算されたモードプロファイルを示しています。 b さまざまなARコーティングを使用した伝達マトリックスシミュレーションに基づいて計算されたモード損失スペクトル

図2bは、シミュレーション中の3つの典型的なモード損失スペクトルを示しています。ここで、高周波数モードと低周波数モードはそれぞれ4.762μmと4.779μmです。 1つ目はARコーティングなしのDFB-QCLです。グレーティングフィードバックから発生した阻止帯域がはっきりとわかり、2つの帯域エッジモードはほぼ同じです。 2つ目は、200 nm Al ₂ による特定のARコーティングです。 O ₃ 反射率0.22の5nmGe。 2つのバンドエッジモードの違いが明らかになり始めます。最後の1つは、反射率の低いコーティングでは、Δモードの損失が非常に大きいため、低周波モードが阻止帯域の損失の下に沈むことを示しています。理論的には反射率が低いほどΔモード損失が大きくなりますが、反射率が極端に低いと、デバイスで大きなミラー損失が発生し、WPEが急激に低下することも考慮する必要があります。これは、実験に基づいて膜厚を選択することのトレードオフです。

デバイス製造

QCLウェーハは、nドープ（Si、3×10 ¹⁷ ）上で成長しました。 cm ^-3 ）2フォノン共鳴設計に基づく固体分子線エピタキシー（MBE）によるInP基板。アクティブコアには、ひずみ補償されたIn _0.669 の40ステージが含まれます Ga _0.331 As / In _0.362 Al _0.638 量子井戸と障壁として、これは参考文献に似ています。 [18]。層の順序は次のとおりです。2μm下のInPクラッド層（Si、2.5×10 ¹⁶ cm ^-3 ）、0.3μmの厚さの一致したIn _0.47 Ga _0.53 層として（Si、4×10 ¹⁶ cm ^-3 ）、40のアクティブ/インジェクターステージ、0.3μmの厚さのIn _0.47 Ga _0.53 層として（Si、4×10 ¹⁶ cm ^-3 ）、3μmの上部InPクラッド層（Si、2.5×10 ¹⁶ cm ^-3 ）、および0.7μmの高濃度にドープされたInPクラッド層（Si、5×10 ¹⁸ cm ^-3 ）。活性領域の平均ドーピングレベルは、経験的に2.4×10 ¹⁶ に調整されました。 cm ^-3 。埋め込みグレーティングを製造するために、上部のクラッドを上部のInGaAs層まで除去しました。周期がΛ=0.755μmの1次DFBグレーティング（デューティサイクルσ =20％）は、ホログラフィックリソグラフィー技術を使用して厚さ300 nmの上部InGaAs層で定義され、その後、湿式化学エッチングによって約90nmの深さまでエッチングされました。次に、厚さ3μmの低ドープ（Si、2.5×10 ¹⁶ cm ^-3 ）InP層に続いて0.2μmを徐々にドープ（1×10 ¹⁷ から変更） cm ^-3 〜3×10 ¹⁷ cm ^-3 ）InP層と0.5μmInP（5×10 ¹⁸ cm ^-3 ）接触層は、有機金属気相成長法（MOVPE）によって上部クラッドとして順番に達成されました。

グレーティングパターンと再成長の実装に続いて、エピウェーハは幅10μmのリッジにエッチングされ、次に導波路がMOVPEシステムに再導入され、半絶縁性InP（Fe）に埋め込まれました。厚さ450nmのSiO ₂ 層は、尾根の周りの絶縁のためにプラズマ化学気相成長法（PECVD）によって堆積され、電気的接触はTi / Au層によって提供されました。続いて、熱放散をさらに改善するために、追加の5μm厚の金層に電気めっきを施しました。導波路は2mmの長さのバーに劈開され、テストは最適化された反射率ファセットコーティングを備えたデバイスで実行されました。 Al ₂ で構成される両方のリアファセットHRコーティング O ₃ / Ti / Au / Ti / Al ₂ O ₃ （400/5/100/10/200 nm）およびAl ₂ で構成されるフロントファセットARコーティング O ₃ / Ge（380/33 nm）は、電子ビーム蒸着によって堆積されます。フロントファセットの計算された反射率は、4.76μmの波長で3.4％であり、コーティングの厚さの変動と反射率の詳細な関係については、以前に公開された論文[19]で説明されています。レーザーは、インジウムはんだを使用してSiCヒートシンクにエピレイヤー側を下にして取り付け、外部コンタクトパッドにワイヤーボンディングしました。スペクトルおよび電気的特性評価では、レーザーをペルチェ素子に取り付け、サーミスタを使用してヒートシンクの温度を監視しました。

結果と考察

図3は、Bruker Vertex 70FTIRと窒素冷却HgCdTe検出器で測定された電流の増加に伴ってエレクトロルミネッセンスからレイジングに動的に変化する閾値下発光スペクトルを示しています。しきい値のすぐ上のレーザースペクトルは、デバイスが基本モードで動作していることを示しており、電流が285mAのときに基本モードの阻止帯域を明確に取得できます。阻止帯域幅からΔν =3.076cm ^-1 および実効インデックス n _eff =1 /（2νΛ）=3.153、結合係数κを計算します =Δν ・π ・ n _eff =30.4cm ^-1 、カップリング製品κLのHRコーティングされた長さ2mmのキャビティの結果 12.1の、これは私たちのデバイス製造によく対応しています。 κLの製品 以前の理論的調査よりもはるかに大きいκL ≈1[20]は、過結合方式が得られることを示します。これは、全電流および検査された温度範囲内でシングルモードを確保するのに有益です。

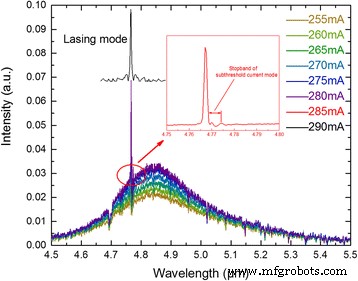
30°Cで測定されたデバイスのしきい値以下のDCスペクトル

図4aは、一般的なCW電力-電流-電圧（ P ）を示しています。 -私 - V ）20〜90°Cのさまざまなヒートシンク温度でのDFBレーザーの曲線。 0.65 kA / cm ² の低しきい値電流密度の2mm長デバイスの出力電力は200mWに達します。 20°Cで。しきい値電圧（ V _th ）13.2〜14.2 Vは、20〜90°Cの温度範囲で測定されました。モードホップは、 P から簡単に推測できる60°C未満の低いヒートシンク温度でのみ存在することに注意してください。 -私 曲線。ヒートシンクの温度が高いと、レーザーコアにさらに深刻な熱が蓄積するため、熱効果によって別のモードのレーザー発振が抑制され、モードホップが発生しなくなります。図4bは、 P を示しています。 -私 - V 反射防止（AR）コーティングが前面に堆積されたDFBレーザーの曲線であり、3.4％のARコーティング反射率を選択します。すべてのスムーズな P -私 曲線は、測定した温度の周囲にモードホップが存在しないことを示しています。図4c、dは、25 mAのステップで150〜250mAのさまざまな電流でのレイジングスペクトルを示しています。図4dから、図4cのモードホップではなく、最適化されたARファセットコーティングを使用して、さまざまな電流の周りで安定したシングルモードを実現していることが明らかです。周波数は常に注入電流と線形関係を保ち、電流調整係数Δν /Δ I =− 0.024cm ⁻¹ mA ^-1 ARコーティングがDFB-QCLのモードホップの問題を解決するためのシンプルで効率的な方法であることを証明します。

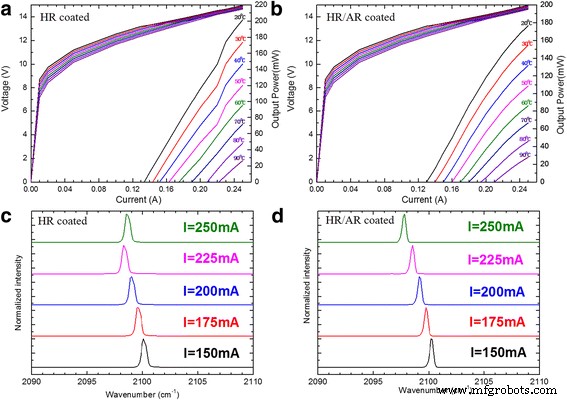
a 、 b V とともに20〜90°Cのさまざまなヒートシンク温度でCWモードで動作するDFBレーザーの出力電力と電流 -私 曲線。 c 、 d 20°Cで25mAのステップで、150〜250mAのさまざまな電流でのCWレイジングスペクトル

図5は、20〜90°Cのさまざまなヒートシンク温度でのコーティングDFBレーザーの発光スペクトルを示しています。測定は、0.25 cm ^-1 のNICOLET8700FTIR分光計を使用して実行されました。 ラピッドスキャンモードでの解像度。単一の縦モード放射が、90°Cの高温でサイドモード抑制比（SMSR）26 dBで、調査された温度範囲全体で観察されます。図5の挿入図に示されているように、ピーク発光スペクトルは2100.4 cm ^-1 からシフトすることが観察されました。 20°C〜2088.6 cm ^-1 90°Cで、温度調整係数Δνに対応 /Δ T =− 0.168 cm ⁻¹ K ^-1 。良好な線形調整は、ヒートシンク温度の変化中にモードホッピングが発生しなかったことを示しました。さらに、言及されたすべてのデバイスは、リッジ幅の正確な制御により、基本モードでのCW動作下で支配的な単一の横方向遠方場を表示します。

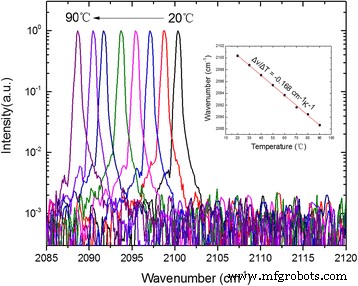
20〜90°Cのさまざまなヒートシンク温度での駆動1.1しきい値電流でのDFBレーザーのシングルモード発光スペクトル。インサートは、温度によるレイジング周波数の線形適合チューニング特性を示しています

CW WPEは、図6に入力電力消費量の関数として計算およびプロットされました。20°Cでは、出力電力170mWで約240mAで最大4.7％のWPEが得られました。最大WPEは、50°Cと90°Cでそれぞれ2.9％と0.8％でした。現在まで、これらの値は、高しきい値のDFB-QCLの場合でも、材料品質が高く、反射率ファセットコーティングが最適化されているため、非常に高くなっています。コーティング効果を考慮したレーザーキャビティ長の最適化された選択により、WPEをさらに改善できると考えられています。

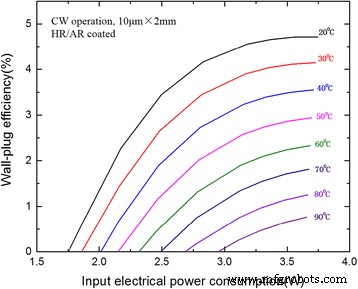
長さ2mmのHRおよびARコーティングされたDFB-QCLの電力損失の関数としてのウォールプラグ効率

結論

λでのシングルモードDFB-QCLの室温CW動作を実証しました 〜4.76μm。二層誘電体Al ₂ からなるARコーティングを堆積することにより O ₃ 前面のGeは、すべての電流および温度条件下でモードホップのない安定したシングルモードを実現することに成功しています。 20°Cでは、170 mWものCW出力電力が観測され、0.65 kA / cm ² という非常に低いしきい値電流密度が観測されています。 。このようなデバイスは、実用的なアプリケーションで中赤外線スペクトル範囲でDFB-QCLの安定したシングルモード動作を使用するための重要なステップを表しています。

略語

AR：

反射防止

BH：

埋もれたヘテロ構造

CW：

連続波

DFB：

分散フィードバック

HR：

高反射

MBE：

分子線エピタキシー

MOVPE：

有機金属気相エピタキシー

PDE：

偏微分方程式

PECVD：

プラズマ化学気相成長法

P -私 - V ：

電力-電流-電圧

QCL：

量子カスケードレーザー

SMSR：

サイドモード抑制率

V _th ：

しきい値電圧

WPE：

ウォールプラグの効率

λ / 4 PS：

1/4波位相シフト