ハイブリッド全誘電体-グラフェンメタ表面に基づく制御可能な複屈折を備えた偏光変換器

背景

ナノフォトニクスの研究は、特に調整可能で実験的に実現可能な光操作メタ表面の設計において、全誘電体要素にシフトしています[1、2]。主な目標は、そのようなメタ表面をナノフォトニックセンシングデバイスに統合することです。誘電体メタ表面への焦点のシフトは、プラズモンメタ表面と比較して、シリコンおよび他の誘電体材料で示される低い放射損失およびオーム損失によるものです。その結果、高Qトラップモード共鳴を使用する特別なプラズモン構造が、伝送効率を高めるために以前に提案されました[2–5]。損失の低減は、離散的な電気モードと磁気モードの間の干渉、または金属元素の対称性の破れのいずれかによって達成されます。自由空間での弱い結合が発生し、損失の低減が強化されます[1、6]。チタニア（TiO ₂ ）などの磁気共鳴を示す材料 ）、窒化ケイ素、およびゲルマニウムは、損失が少ないため、電磁スペクトルのさまざまな領域で優れた光学特性を示します[7–9]。特に、可視分散が低く、電気光学特性が強いため、低コントラストのメタ表面光学素子の設計に使用できます。

最近、グラフェンベースのファノ共鳴メタサーフェスが、変調器[10–13]、吸収体[14、15]、低速光デバイス[16、17]、マント[16、18]などの光操作デバイス用に提案されました。他の人と同様に。これらのデバイスでは、単分子層グラフェンと共鳴ギャップ内の閉じ込められた電界との間の強い相互作用の結果として、放射損失が軽減されました。グラフェンは、調整可能な光伝導度や高いキャリア移動度など、優れた特性を提供します。これにより、放射損失が抑制された高Q共振構造をサポートできます[19、20]。一方、金属メタ表面は、サブ波長要素を利用して電界の閉じ込めを強化し、衝突する光の位相、振幅、および偏光に急激な変化をもたらします。

スプリットリング共振器（SRR）は、光学特性を柔軟に調整できるインダクタンス-静電容量共振の性質があるため、一般的なプラズモンメタ表面要素です。同様に、他の誘電体メタ表面も、調整可能性と製造能力のために、基本的なメタ表面ユニットとしてSRRを採用しています[21、22]。シリコン膜上の「Zスロット」などの他の要素形状も、偏光スプリッターとして設計されています[23]。ただし、金属メタ表面はオーム損失が高く、透過率が低いため、光操作の効率が低下します[24、25]。

Chenらによって提案された全誘電体メタデバイスおよび勾配格子偏光変換器。とKruket al。は、驚くべき効率を示しています〜99 ％ [26、27]。構造は、テラヘルツ領域と近赤外領域で、それぞれ0.35と0.9の高い複屈折比を示します。ただし、複屈折調整メカニズムは提案されていません。この作業では、複屈折の調整可能性とスイッチングがゲート電圧バイアスによって示され、構造の柔軟性が寸法変化によって示されます。通常、高屈折率アンテナから構築されたメタサーフェスは、インピーダンスの不一致による部分的な後方反射の存在によって制限されます。この課題を克服する方法は、強力な局所的な電気的および磁気的三重型共鳴を備えたシリコンメタ表面を設計して、ほぼ単一の透過を実現できるようにすることです[28–30]。一方、高コントラストのメタサーフェスは、効率は高くなりますが、格子線に沿った正確な位相または偏光プロファイルを実現するための空間分解能は低くなります[31、32]。

この作業では、トラップされた磁気モードに基づいてQ値が高い全誘電体メタサーフェスが示されています。提案されたユニットセルは、シリコン、グラフェン、およびシリカ基板で作られた十字型の非対称の長方形の双極子で構成されています。グラフェン層はシリコンとシリカの間に挟まれています。光の偏光の制御は、グラフェンの固有の特性とシリコンの寸法によって実現され、4分の1波長板の特性を示します。したがって、入射する直線偏光は、近赤外（> 95 ％）で高い偏光変換率（PCR）で円偏光に変換されます。 ）。さらに、散乱光の円偏光状態は、外部ゲート電圧バイアスを介して、右回りの円偏光（RCP）状態と左回りの円偏光（LCP）状態の間で切り替えることができます。この偏光の動的制御により、構造の自由度が高まり、CMOSフォトニックデバイスに大きな影響を与える可能性があります。 COMSOL Multiphysicsを使用した有限要素法を使用して、ユニットセルをモデル化し、メタサーフェスのパフォーマンスを分析しました。

メソッド

構造のユニットセルの概略図を図1aに示します。これは、グラフェン層の上部にあるシリコンの十字型アンテナとシリカ基板で構成されています。シリコンとシリカの比誘電率はそれぞれ12.25と2.25です[33]。すべての寸法は図1aのキャプションに示されています。まず、許容できる共振を得るために、周期性 P _x =600 nmが固定され、 P _y いくつかの値にまたがってスイープしました。内部寸法 L ₁ =440nmおよび L ₂ =370 nmも固定されたままでしたが、後で位相調整用に最適化されました。高さ h =110nmおよび幅 W =60 nmは、シミュレーション全体を通して固定されたままでした。ポートソースからの通常の入射光、周期境界、および出口端の完全一致層が使用されました。

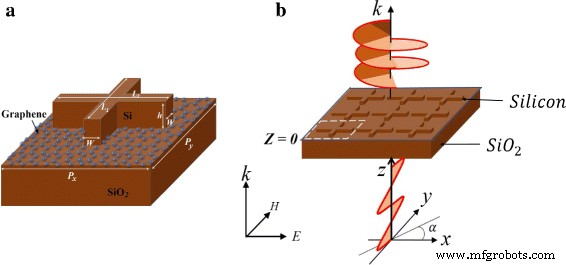
概略図。 a。 ユニットセルの寸法： L ₁ =450 nm、 L ₂ =370 nm、 h =110 nm、 W =60 nm、 P _x =600 nm、および P _y =560nm。 b。 偏光角αでの入射直線偏光 、構造を介して円偏光に変換されます

光の透過特性は、散乱電場 E に基づいて定義されました。 _i （ i = x 、 y ）、つまり、\（T_ {xx} =\ left | \ frac {E_ {x}} {E_ {0}} \ right | \）、\（T_ {yy} =\ left | \ frac {E_ {y }} {E_ {0}} \ right | \）、Φ _xx =arg（ E _x ）、およびΦ _yy =arg（ E _y ）、ここで T _ii （ i = x 、 y ）は透過係数とΦ _ii （ i = x 、 y ）はフェーズコンポーネントです。次に、位相遅延を\（\ Delta \ Phi =\ text {arg} \ left（\ frac {E_ {x}} {E_ {y}} \ right）=\ Phi _ {xx}-\ Phi_として定義しました。 {yy} \）そして距離 z で計算しました =1.2 μ 表面からm。複屈折メタサーフェスは、透過フィールドのコンポーネントの1つに位相遅延を導入することにより、入射光の偏光状態を操作します。ホイヘンスの原理により、構造はΦの間に位相の不連続性と位相遅延を作成します _xx およびΦ _yy 透過光の\（E =E_ {x} e ^ {i \ Phi _ {xx}} \ hat {x} + E_ {y} e ^ {i \ Phi _ {yy}} \ hat {y} \ ）。導入された位相遅延が90°または− 90°の場合、LCPまたはRCPライトがそれぞれ生成され、図1bに示すようにQWPの動作が確認されます。一般に、メタサーフェスを通過する送信波は楕円偏波です。

通常、グラフェンの光学特性は、その導電率σによって表されます。 、バンド間遷移とバンド内遷移の両方を特徴とする：σ =σ _私 + σ _D 、ここでσ _私 およびσ _D それぞれ、バンド間およびバンド内の導電率です。表面電荷密度の変化、 n _s 、グラフェンでは、グラフェンの電子集団とフェルミエネルギーが変化します。つまり、\（E_ {F} =\ hbar \ nu _ {F}（\ pi n_ {s}）^ {1/2} \）、ここでν _F =10 ⁶ m / sは電子のフェルミ速度です。グラフェンを、厚さδのメッシュセルのバルク単層としてモデル化しました。 =1nm、面内寸法、1nm×1nm。面内誘電率は、室温でのランダム位相近似内で計算されました。\（\ epsilon _ {g}（\ omega）=1+ \ frac {i \ sigma} {\ omega \ epsilon _ {0} \ delta} =\ epsilon '+ i \ epsilon' '\）、ここでε ^' およびε ^″ は、それぞれ、誘電率の実数部と虚数部であり、入射光子エネルギー\（E =\ hbar \ omega \）と E の関数として定義されます。 _F ：

ここで、Γ =110 meVは、近赤外およびτでバンド間遷移の広がりをもたらすエネルギーです。 は自由キャリア散乱率です。パラメータ\（\ frac {1} {\ tau} \）は、近赤外線でのバンド内遷移よりもバンド間遷移が優勢であるため、ゼロと見なされます[1]。

結果と考察

フェルミエネルギーと構造の寸法による複屈折制御

まず、グラフェン層のない全誘電体メタ表面をシミュレートし、図2aに示す透過スペクトルを取得しました。構造は、偏光角αで入射直線偏光（LP）によって照らされました。 、図1bに示すように。図2aの透過率の結果は、Q値が高い狭い共振を示しています。これは、トラップされた磁気モードの励起に起因します。共鳴波長λには強い面内電界があります =1.49 μ アンテナの端に沿ってm（図2b）。面内電界は逆平行であり、電気双極子応答と磁気双極子応答の間に破壊的な干渉効果を引き起こします。偏光角αでの入射LP光の成分 =48°、トラップされた電磁モードと自由空間光の間に弱い結合を引き起こします。さらに、シリコン双極子への強い電界浸透により、鋭い位相シフトが発生し、入射平面波と循環変位電流の間の結合が強化されます。図3a、bに示すように、強い磁気共鳴と急激な相変化が共鳴波長で発生します。磁気ダイポールモードは、電気モードよりも円形変位電流の影響を受けます。これは主に、隣接するアンテナダイポール間の結合によるものです。さらに、Kirshav etal。磁気共鳴は構造の寸法と形状によって影響を受けることを実証しました[34]。たとえば、私たちの構造では、入射光の横方向の寸法と波長は、\（L_ {i}（i〜 =〜1,2）\ approx \ frac {\ lambda} {n _ {\ text { si}}} \）、ここで L _i 約440nmおよび n _si =3.5。

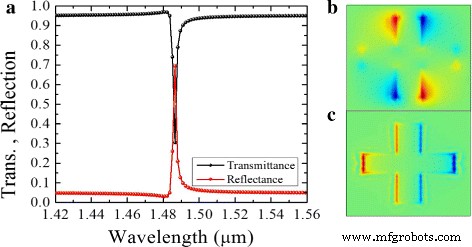
a グラフェンを含まない誘電体構造の透過と反射。 b 、 c 。面内電界 E _x （b）および E _v （c）、共振波長λで計算 =1.49 μ m

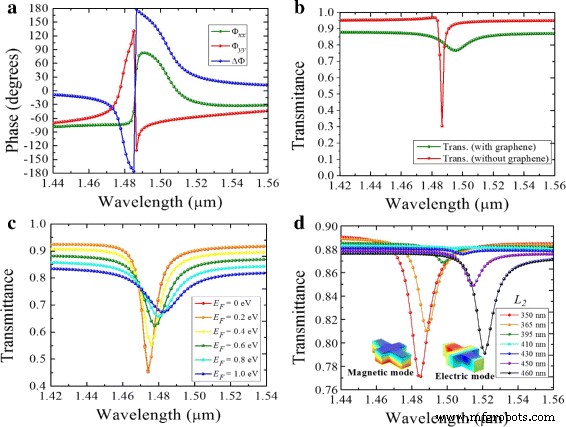
a グラフェンを含まない全誘電体メタ表面の相成分とリターデーション。 L の波長の関数としてプロットされた透過率 ₁ =440 nm、 L ₂ =370 nm、および W =60 nm、 b の場合 グラフェンを含まない構造とグラフェンを含む構造（ E _F =0.8 eV）、 c 変化するフェルミエネルギー、および d さまざまな L ₂ 350から450nmまで。 L で対称性の破れ ₂ =410 nmは、磁気と電気の2つの主要なモードを分割します

グラフェン層を基板とナノアンテナの間に挿入すると、シリコンアンテナ内の循環変位電流が減少し、表面電界が増強されます。これは、入射電界の分極がナノアンテナの反対側の境界で反平行であり、要素内の循環変位電流との弱い結合を引き起こす状態に対応します。グラフェンは、シリコンとシリカ基板の間の表面に強化された伝導を導入します。エレメント内の変位電流との結合と比較して、面内電界とのより強い結合が発生します。この効果により、図3bに示すように、表面に破壊的な干渉を引き起こす逆平行電界が減少し、Q値が大幅に低下します。共振波長もλからわずかにシフトします =1.49 μ mからλ =1.5 μ mシリコンへの浸透が減少したため。図3cに、グラフェンのフェルミエネルギーを変化させた場合の効果を示します。ドープされていないグラフェンの場合（ E _F =0 eV）、λに強い共鳴があります =1.5 μ mは、ドーピングレベルが増加するにつれて減少します。フェルミ準位が低く、グラフェンがより大きなεの誘電特性を示す場合、バンド間遷移が支配的になります。 ^' 。ただし、 E _F が増加すると、いくつかのバンド間遷移チャネルがブロックされます。バンド内遷移は、グラフェンの誘導応答を引き起こし、その吸収を減少させます[1,20]。グラフェンの下層とシリコン構造の適切な寸法により、磁気および電気双極子モードの強度を高め、高い散乱効率を実現できることは注目に値します[34]。シリコンアンテナは、図3dに示すように、共振の周りの2つの近い波長からの結合共振を示します。 λで =1.48 μ m、アンテナはλにある間、誘導された磁気双極子の結合を示します =1.52 μ m、結合は電気モード間です。 2つのモードは、アンテナの対称性が x から変化したときに発生します。 y L での向き ₂ 約410nm。寸法 L ₂ L を維持しながら、350〜480nmの範囲の値をスイープしました ₁ 440nmで固定。

グラフェン効果は、透過電界の位相成分と位相遅延を調整するのに役立ちます。まず、入射LP光の成分がシリコンアンテナの直交アームに分解されます。各双極子共鳴は、散乱光に異なる位相パターンを刻印します。具体的には、共鳴の近くで、各双極子共鳴は、[− πの範囲で入射電場の位相をシフトします。 、π ]。アンテナの適切な寸法で、図4aに示すように90°の位相差が得られます。対応する透過係数を図4bに示します。交点 T が目立ちます _xx = T _yy 共振の近くで発生し、理想的なQWP条件を定義します。さらに、長さ L のさまざまな値をスイープすることによって ₂ L を維持しながら ₁ 修正済み（ L ₁ =440 nm）、さまざまな電気モードと磁気モードに関連する共振振幅を変えることができます。 L の場合、±10°以内の許容可能な位相帯域幅範囲が得られました。 ₂ =RCPの場合は365nm、 L ₂ =図4cに示すように、LCPの場合は450nm。次に、図4dでは、グラフェンのフェルミエネルギーを変化させることにより、それに応じて位相帯域幅が変化します。 λで =1.48 μ m、ドープされていないグラフェン（ E _F =0 e V ）シリコン双極子への電界の高い浸透と x 間の大きな位相差を引き起こします および y 散乱光の成分（約150°）が発生します。ただし、 E として _F 0.8 e に近づく V 、面内プロパティ（ε _x =ε _y ）グラフェンの表面伝導率を高め、シリコンへの浸透を減らし、Δ Φ λで約90° =1.49 μ m。

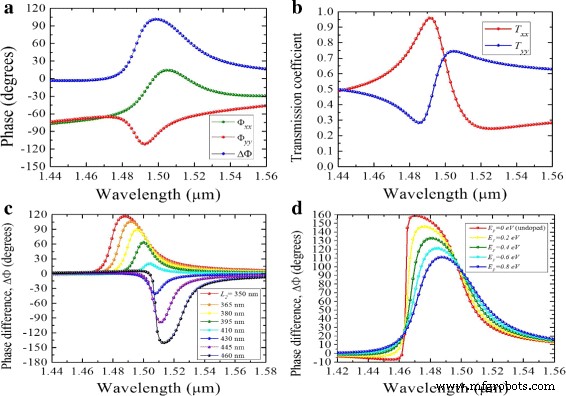
a 全誘電体/グラフェンメタ表面と b の相成分とリターデーション 対応する透過係数 T _xx および T _yy 。 L の波長の関数としてプロットされた位相遅延 ₁ =440 nm、 L ₂ =370 nm、および W =60 nm、 c の場合 変化するフェルミエネルギーと d さまざまな L ₂ 350〜450 nm

L を使用したハイブリッド構造の計算されたストークスパラメータと偏光楕円の寸法 ₁ =450 nm、 L ₂ =370 nm、および W =60 nmを図5a、bに示します。共鳴波長から離れると、透過光の偏光は入射光の偏光と変わらないことに注意されたい。ただし、共鳴の近くでは、入射LP光の偏光状態は円形に変化します。 λで =1.5 μ m、ストークスパラメータ比| S ₃ / S ₀ |≈±1、ここで+ 1値は完全なRCPを示し、-1は完全なLCP出力を示します。ここで、 S ₀ =| E _x | ² + | E _y | ² および S ₃ =2 E _x E _y sin Δ Φ ストークスパラメータです。透過強度の程度は S によって決定されます ₀ 、つまり、値> 50 ％ 許容範囲です。図5cは、透過係数から計算されたPCR効率を示しています。

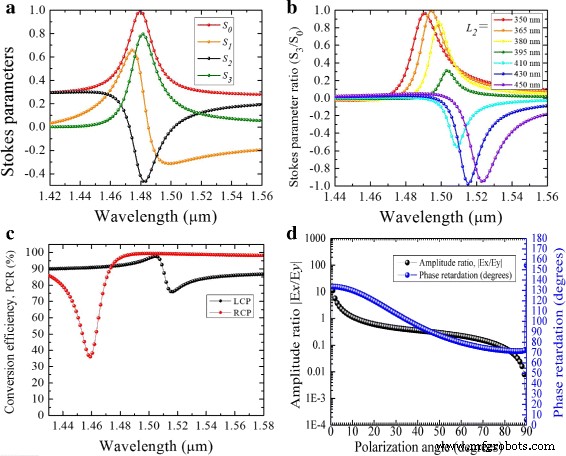
a 入射偏光角αの波長に対するストークスパラメータの変化 =48°。 b 。ストークスパラメータ比（ S ₃ / S ₀ ） L の関数としての変動 ₂ αで a に記載 、 c 入射直線偏光に対して計算された偏光変換率。 d 。波長λでの振幅と位相差の比率 =1.5 μ 偏光角の関数としてのm

ここで T _yx および T _xx それぞれ、交差偏波と共偏波の項です。波長範囲内λ =1.48 μ mとλ =1.51 μ m、効率は約96 ％ RCPおよび≈90％の場合 LCP出力用。ただし、λでは =1.52 μ m、効率はわずかに約80 ％に低下します LCPの場合。図5dに示すように、構造は入射LP光の偏光角の影響を受けません。許容振幅比 E _x / E _y ≈1および位相シフトΔ Φ 広い範囲で約90°が得られます。 αの場合 =48°、正確なQWP条件が得られます

さらに、フォーム複屈折を定義する透過位相プロファイルは、周期性 P の関数として計算されました。 _i （ i = x 、 y ）波長λ =1.49 μ m。図6aでは、構造の調整可能な位相遅延は、2つの周期性が逆の関係を示す対角線に沿って得られます。位相遅延（Δ）も注目に値します。 Φ 図6bに示すように、透過率が80％を超える領域で約90°）が発生します。シリコンとシリカは分散が低く、屈折率が比較的高いため、短波長での低吸収をサポートします[8]。同様に、位相出力は外部ゲート電圧を介して制御できます。

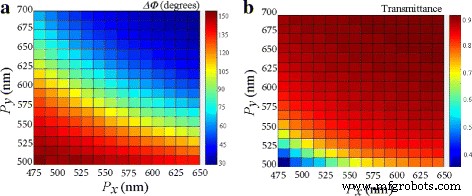
a – b 周期性の変化 P _x および P _y λで =1.5 μ m。 a 送信フェーズと b 透過率

ゲート電圧バイアスによる複屈折スイッチング

y の両端にゲート電圧バイアスをかける -シリコン/グラフェン構造の平面は、図7aに示すように設計されました。ゲート電圧を順方向バイアス値と逆方向バイアス値の間で切り替えることにより、入射LP光は散乱光のRCP状態とLCP状態​​にそれぞれ動的に変換されます。バイアス電圧は、電子のフェルミ速度νを制御します。 _F 、電子の流れの方向を切り替えます。さらに、バイアス電圧はグラフェンのキャリア密度を変化させ、それが次にその電気伝導率と誘電率の変化につながります。この構成では、構造は、単位面積あたりの静電容量 C を持つ準平行板コンデンサモデルを形成します。 、 C として定義 =ε _si ε ₀ / P _x 、ここでε _si はシリコンの誘電率です。フェルミエネルギー\（E_ {F}〜=〜\ hbar \ nu _ {F} \ sqrt {\ pi n_ {s}} \）も変調されます。電荷密度（ n _s ）および単位面積あたりの静電容量（ C ）ゲート電圧、つまり n を介してフェルミエネルギーをスケーリングします。 _s = C V _G / e 。その結果、 P の増分 _x グラフェンのキャリア濃度と単位面積あたりの静電容量の両方を減少させます。その結果、図7bに示すように、位相遅延の位置は赤方偏移し、中赤外線の摂動理論と一致します[35]。

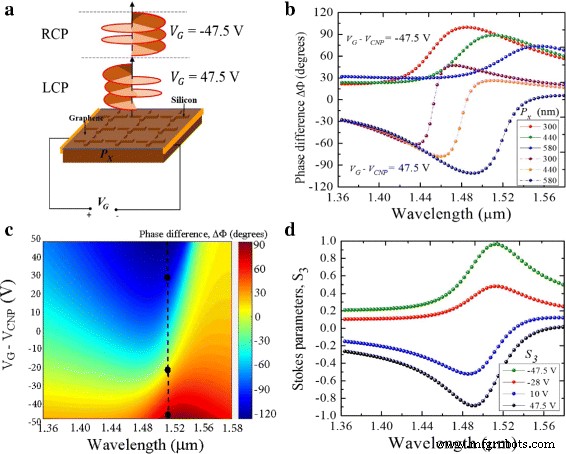
a ゲート電圧バイアスによる分極状態のシリコン/グラフェンスイッチングの概略図。 b。 ゲート電圧バイアスの関数としてシミュレートされた位相差。 c。 周期性の関数として示される位相差 P _x とゲート電圧。 d。 ストークスパラメータ S ₃ 異なるゲート電圧によって定義される円偏光の2つの状態を示すスペクトル

λで =1.5 μ m、円偏光の2つの状態は、0と1の2つのバイナリ状態としてエンコードできます。論理状態0は、逆電圧-47.5 V に対応します。 一方、論理状態1は順方向電圧47.5 V に対応します。 、図7cに示すように。位相遅延のごくわずかな変化、Δ Φ 約0°、ゲート電圧が− 25 V のときに観察できます （図の黒い点線に沿って）。この観察結果は、-47.5、-25、および47.5 V での相変化における非線形応答を示しています。 、キャリア密度とゲート電圧の変化によりグラフェンがより導電性になるにつれて、容量結合が変化することに起因します。近赤外線の他の波長と比較して、1.5 μ mは、散乱光の円偏光状態を切り替えるための最適なポイントを示しています。

図7dでは、ストークスパラメータ S ₃ は、ゲート電圧バイアスの結果としての円偏光の程度を示しています。 − 1および1の限界は、それぞれ線形状態からLCPおよびRCP状態への理想的な偏光変換を示します。波長間λ =1.49 μ mとλ =1.52 μ m、円偏光度は1に近づきます（> 90 ％ ）両方の状態について、構造の最も適切な操作領域をQWPとして確認します。

図8a、bは、 z の位相分布を示しています。 設計波長λで計算された電界の成分 =1.5 μ m at z =0。電圧が47.5から-47.5 V に反転すると、分布がシフトします。 。グラフェンの電気伝導率とキャリア密度の変化により、シリコン構造の周りにトラップされた磁気モードが回転します。

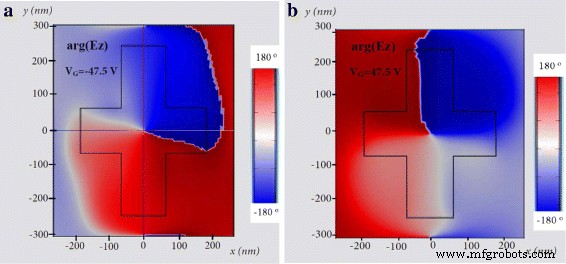
電界成分の位相マップ E _z z のシリコン/グラフェンの十字型構造を介して =0設計波長λで計算 =1.5 μ m、 a ゲート電圧が V の場合 _G =− 47.5 V 、および b ゲート電圧が V の場合 _G =47.5 V

結論

要約すると、ハイブリッドシリコン/グラフェンメタ表面偏光コンバータの複屈折可制御性は数値的に設計されています。トラップされた磁気モードと高いQ値は、グラフェンとシリコンを統合することによって変調されます。ハイブリッド構造の2つの構成が示されています。1つはゲート電圧バイアスあり、もう1つはゲート電圧バイアスなしです。電圧バイアス構造では、複屈折性能はゲート電圧の反転によって示されます。入射LPライトから、逆バイアス電圧（-47.5 V）がRCP出力を生成し、順バイアス電圧（47.5 V）がLCP出力を生成します。したがって、動的スイッチング性能が達成されます。自由空間構成の場合、QWPのパフォーマンスは、シリコンの寸法とグラフェンのフェルミ準位を操作することで示されます。どちらの設計でも、グラフェンのない構造よりも安定した広い帯域幅が得られます。設計は、より高度な偏光変換を示しています（> 96 ％ ）近赤外線（λ =1.45〜1.54 μ m）。プラズモンメタ表面とは異なり、これらの成果は、放射損失やオーミック損失のない高効率を示しています。さらに、構造はコンパクトで非常に薄いため、CMOSおよびフォトニックデバイスとの互換性と統合に適しています。一方、グラフェンは実現可能であり、基板上に化学蒸着を使用して成長させることができますが、シリコン構造は標準的なリソグラフィー法を使用して製造することができます。