非対称メタマテリアル共振器に基づくテラヘルツ周波数での高Qファノ共鳴

背景

メタマテリアルは、負の屈折率[1]や超高屈折率[2]など、ほとんどの状況で天然素材では実現できないエキゾチックな特性を示す一種の人工材料です。このような人工材料は、大量の周期的な金属ユニットで構成されており、ユニットの幾何学的パラメータを変更することで、その特性（誘電率や透磁率など）を簡単に制御できます[3]。その結果、近年、メタマテリアルの研究が広く注目されています。この領域では、完全な吸収[4、5]、メタマテリアルセンサー[6、7、8、9]、クローキング[10]、ファノ効果[11]など、非常に多くの新しいアプリケーションが登場しています。

ファノ共鳴の線形状は、対称ローレンツプロファイルとはかなり異なります。非対称でシャープで、 Q が比較的高くなっています。 -要素。ファノは理論的にファノ共鳴の量子メカニズムを明らかにして以来[12]、それはホットな話題になっています。ファノ共鳴の起源を説明するために、ファノの量子力学的解析[12]、古典的な振動子モデル[13]、結合モード理論[14]、ファノ共鳴の電磁理論[15、16]などのいくつかの理論が設定されています。 。 GallinetとMartinによって提案されたファノ共鳴の電磁理論[16]によると、特徴的なファノプロファイルは、非放射モードと連続体としても見ることができる放射モードの間の結合に起因します。

テラヘルツレジームでは、メタマテリアルに弱い非対称性を導入することで鋭いファノ共鳴を実現できます[17、18、19、20]。これにより、基礎となるダークモードが出現する可能性があります[21]。さらに、グラフェン材料を利用して、ファノ共鳴を生成し、さらには変調することもできます[22、23]。 EIT（電磁誘導透明度）[24、25]およびPIT（プラズモン誘導透明度）[26、27]の大部分と比較して、ファノ線の形状ははるかに鋭く、狭くなっています。 Q -ファノの係数[17、28]プロファイルは、多くの状況でローレンツの線形状[29、30、31]の約10倍です。この特性により、ファノ共鳴は高感度検出を実現するための有望な選択肢になります[8]。ただし、 Q -多くのメタマテリアルの係数は十分に高くないため[17、32、33]、センシングの観点からそれらのアプリケーションを制限します。ファノ共鳴をセンシングに広く効率的に適用するには、 Q を大幅に改善する必要があります。 -メタサーフェスの係数。

最近、いくつかのメタマテリアル構造は、高い Q を実現するように設計されています。 ファノ共鳴。たとえば、Ding etal。異なる幾何学的パラメータを持つ非対称スプリットリングの2つのセットで構成される二重層メタマテリアルを提案しました。 Q の3つのファノ共鳴をサポートできます -係数はそれぞれ33、42、および25です[19]。 Q を改善するために、各層に同一のスピットリング共振器で構成される対称二量体構造も提示されました。 -ファクター[34]。ただし、これらの積み重ねられた構造は、製造における技術的な課題に苦しんでいます。高- Q シンプルな構造設計との共鳴は、依然としてホットな問題です。

この論文では、4つの金属ストリップで構成される共面メタマテリアル構造を示します。各ユニットセルには、3つの平行なストリップが4番目のストリップに垂直に配置されています。この構造は、高い Q をサポートできます ファノ共鳴（ Q -値は、25％の透過率で0.81THzで約58）です。この鋭い線の形は、明るい（放射）モードと暗い（非放射）モードの間の相互作用に由来します。さらなる議論のために、ファノ共鳴の電磁理論が採用されています[15、16]。ファノ共鳴の特性は、幾何学的パラメーターの制御を介して変更できます。デバイスのセンシング性能について説明します。さらに、元々設計された構造にさらにストリップを追加することで、複数のファノ共鳴を実現できます。

メソッド/実験

大量の研究により、構造の対称性を破ると、非対称のファノライン形状が誘発される可能性があることが示されています[17、18、35、36、37]。このコンセプトに基づいて、図1に示すこの4ストリップのメタマテリアルを設計します。ここで、ストリップ2は、対称性の破れを実現するように設定されています。図1aは、提案されたメタマテリアルの3次元図を示しています。図1b、cは、それぞれ構造ユニットの側面図と上面図を示しています。金属製の4ストリップ共振器は、屈折率の実数部が1.5、虚数部が0の理想的な誘電体基板の上部に配置されます。実際には、この誘電体材料はシリカに対応しています。つまり、テラヘルツ領域では基板は無損失です。導電率σのAuを選択します =4.09×10 ⁷ 厚さが0.2μmの金属平面共振器を形成するためのS / m。繰り返し期間は P _x = P _y =180μm。 3つの平行なストリップ（1、2、および3）は同じサイズです。それらの長さは l _x =120μm、幅は w =20μm。ストリップ4は、他のストリップ（1、2、および3）に垂直です。その長さは l _y =150μm、幅は w =20μm。ストリップ2の軸と構造の中心点の間の距離は d です。 =30μm。有限差分時間領域法を使用して、この平面メタマテリアルをシミュレートします。シミュレーション時間と計算メモリを節約するために、Δ x のメッシュサイズを選択します。 =Δ y =1μmおよびΔ z =0.02μm。この場合、シミュレーション結果は非常に正確であることがわかります。より小さなメッシュサイズが適用されても、シミュレーション結果はほとんど変わりません。 x に沿った境界条件のシミュレーション -軸と y -軸は周期的に設定され、 z に沿った条件 -軸は完全一致レイヤーとして設定されます。図1aは、構造全体が垂直に入射するTHz波のビームで照らされていることを示しています。図1b、cに見られるように、電気ベクトル E および磁気ベクトル H 入射テラヘルツビームの y -軸偏光および x -それぞれ偏光された軸。

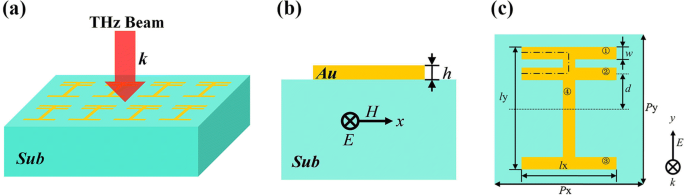
提案されたメタマテリアルの3次元図（ a ）。側面図（ b ）および上面図（ c ）非対称メタマテリアル共振器の;同等の長さ l 一点鎖線でマークされています

結果と考察

提案されたメタサーフェスの透過スペクトルを図2aに示します。 0.430THzと0.809THzの周波数で2つの伝送ディップがあり、伝送速度はそれぞれ0.10％と26.45％です。以下の説明をより簡潔にするために、 R を使用します。 _s R _s および R _d これらの2つの共振モードをマークするには、 R _s 0.430THzおよび R で共振するモードの場合 _d より高い周波数での共振モードの場合。 R の光伝送速度 _s は、0.256THzの比較的広い帯域幅を持つ対称ローレンツプロファイルを示しています。比較すると、 R _d 0.014THzの帯域幅ではるかにシャープな非対称ファノライン形状を示します。 Q -係数は、線の形状を判断するための重要な基準です。中心周波数を帯域幅で割ることで得られます。実際、 Q - R の係数 _d Q の30倍の58に達することができます - R の値 _s 、これは多くの分野で基盤となるアプリケーションに貢献します。ダークモードとブライトモードの間の相互作用、つまり非放射状態と連続体の間の相互作用に非対称ファノプロファイルのルーツが存在することは、放射状態から生成されます[16、38、39]。この論文の残りの部分では、ファノライン形状の詳細なメカニズムについて説明し、理論的な透過スペクトルを分析します。提案されたメタサーフェスでは、0.809 THzでの透過率は26.45％ですが、さらに低減することができます。 [40、41]によると、損失のある誘電体材料を使用すると、透過率が低下する可能性があります。シミュレーションでは、選択した基板材料は、テラヘルツ領域で損失のない、実際の屈折率が1.5の理想的な材料です。透過率を低減するための実行可能な方法は、この理想的な無損失材料ではなく、複雑な屈折率を持つ損失材料を使用して基板を形成することです。

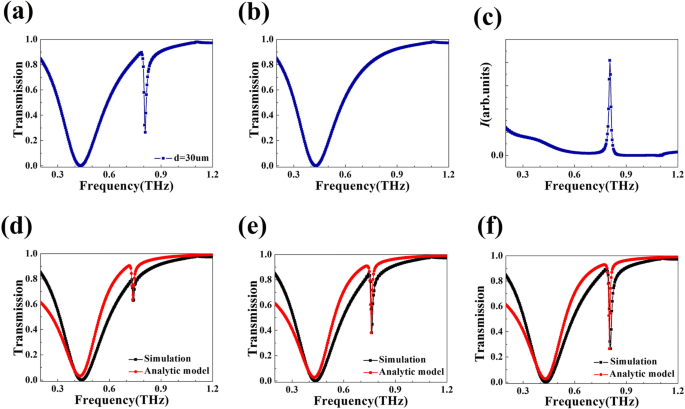
a 数値シミュレーションによって与えられた設計されたメタ表面の透過率曲線。 b ブライトモードの透過スペクトル。 c 双極子源によって照らされた提案された4ストリップナノ構造の電界強度。 d 、 e 、 f d を使用して設計された構造のシミュレーション（赤い曲線）および理論（黒い曲線）の透過スペクトル =10μm、 d =20μm、および d =それぞれ30μm

透過率曲線の原点を把握するために、電界の分布∣ E ∣と z 磁場の成分（ H _Z ）2つの共振ディップの中心周波数での値を図3に示します。 R の電界分布には大きな違いがあります。 _s および R _d 。図3aは、共振モード R の電界を示しています。 _s 主にストリップ1とストリップ3、特にこれら2つのストリップの端に集中しています。ただし、ストリップ2やストリップ4など、構造の他の部分の電界分布はほとんどありません。このような電界分布は、電気ベクトルが E y に沿っています -軸。したがって、 R _s 基本共振（つまり、局所的な電磁EM（電磁）応答）と見なすことができます[42]。その上、 z の分布 磁場の成分（ H _Z ）モード R の場合 _s を図3bに示します。ここから、表面電流分布を取得できます。表面電流の分析は、モードの結合がファノ共鳴をどのように生成するかを明らかにするための重要な方法として役立つことが実証されています[28]。図3bに示すように、表面電流は構造の下部から上部に流れ、ストリップ1とストリップ3の両側に反対の電荷を集めることに寄与します。対照的に、中心周波数 R _d かなり違います。ストリップ1とストリップ2の周囲に強い電界が見られ（図3c）、これはモード R の約4倍です。 _s 。 H の分布によると _Z 図3dに示すフィールドでは、表面電流がストリップ1とストリップ2の間を上向きに流れ、ストリップ2とストリップ3の間の電流が反対方向に流れることが明らかです。マクロレベルでは、このような電界分布は、水平ストリップ間のある種の電荷誘導と見なすことができます。モード結合の観点から、この現象は明るいモードと暗いモードの間の相互作用によるものです。

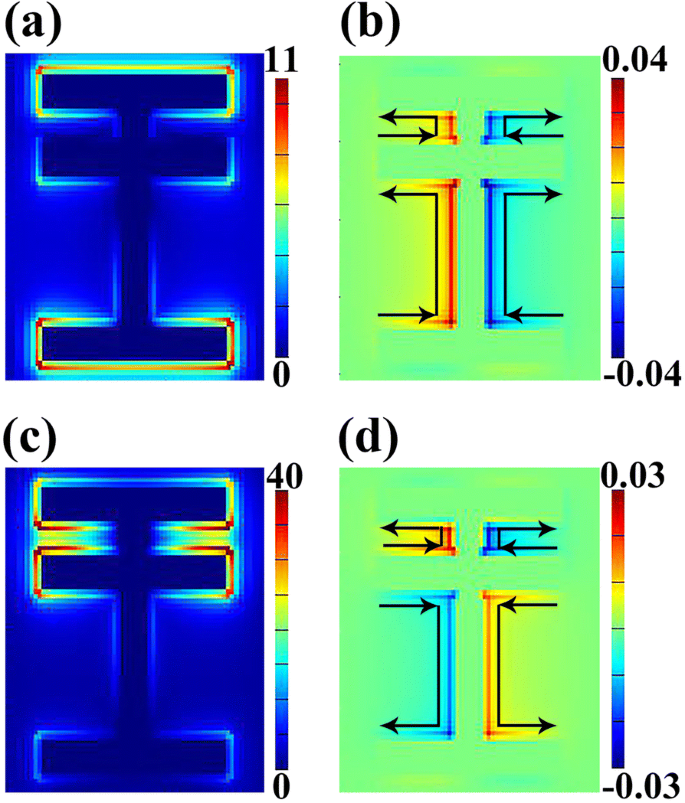
電界の分布∣E∣（ a ）および z 磁場の成分（H _Z ）（ b ）0.430 THz（ R _s ）; ∣E∣の分布（ c ）およびH _Z （ d ）0.809 THz（ R _d ）; b の黒い矢印 および d 表面電流の方向を表す

説明を深めて定量化することを目的として、明るいモードと暗いモードのスペクトルをシミュレートし、ファノ共鳴の電磁理論[15、16]を提案構造で使用します。図2bは、周期単位がストリップ1、3、および4で構成される構造の透過スペクトルを示しています。このような構造によってサポートされる共振モードは、平面波によって直接励起できます。したがって、これは「ブライトモード」です。対照的に、ダークモードは平面波のビームによって励起することはできません。それは、急速に変化する場、例えば、双極子の近接場を通して励起することができます[15、43]。図2cは、双極子源によって照らされた4ストリップメタマテリアルの電界強度を示しています[44]。マクスウェルの方程式は、ナノ構造におけるファノ共鳴の電磁理論の確固たる基盤を形成します。マクスウェルの方程式によると、電気ベクトル E 以下の波動方程式に従います：

$$ {\ in} ^ {-1} \ left（\ mathbf {r}、\ upomega \ right）\ nabla \ times \ nabla \ times \ mathbf {E} \ left（\ mathbf {r}、\ upomega \右）-\ frac {\ upomega ^ 2} {{\ mathrm {c}} ^ 2} \ mathbf {E} \ left（\ mathbf {r}、\ upomega \ right）=0 $$（1）

ここで、ωは入射ビームの周波数であり、∈（ r 、ω）は、損失のある材料の複素誘電率です。電界 E 誘電率∈は、周波数ωと位置ベクトル r の両方に関連しています。 。 2つの正射影演算子PとQを使用して、波動関数∣ E を分離できます。>明るいモードにP∣ E >およびダークモードQ∣ E >、すなわち、放射モードと非放射モード[15、38]。複雑な導出により、明るいモードの強さに対する全フィールドの強さの比率は、次のように与えることができます

$$ {I} _ {\ mathrm {a}} \ left（\ upomega \ right）=\ frac {{\ left（\ frac {\ upomega ^ 2-{\ upomega _ {\ mathrm {a}}} ^ 2 } {2 {W} _ {\ mathrm {a}} {\ upomega} _ {\ mathrm {a}}} + q \ right）} ^ 2 + b} {{\ left（\ frac {\ upomega ^ 2 -{\ upomega _ {\ mathrm {a}}} ^ 2} {2 {W} _ {\ mathrm {a}} {\ upomega} _ {\ mathrm {a}}} \ right）} ^ 2 + 1} $$（2）

ここで W _a およびω _a は、それぞれ非対称共振の帯域幅と中心周波数です。非対称パラメータ q および変調減衰パラメータ b どちらも I を説明するために不可欠です _a （ω）[15、16]。式。 （2）は、 I _a （ω）は非対称のプロファイルを示し、最終的に透過率曲線に非対称のファノライン形状をもたらします。

明るいモードの強度 R _s 滑らかなローレンツプロファイルに従います。これは周波数ωに依存し、次の式に従います。

$$ {I} _ {\ mathrm {s}} \ left（\ upomega \ right）=\ frac {a ^ 2} {{\ left（\ frac {\ omega ^ 2-{\ omega _ {\ mathrm {s }}} ^ 2} {2 {W} _ {\ mathrm {s}} {\ omega} _ {\ mathrm {s}}} \ right）} ^ 2 + 1} $$（3）

そのうち W _s およびω _s それぞれ、図2bに表示されているスペクトルの帯域幅と中心周波数、および a は共振の振幅の最大値です。総力 I （ω ）の共振は、 I の積で計算できます。 _a および私 _s 、最終的に透過率を取得できます T （ω）。

$$ I \ left（\ omega \ right）={I} _ {\ mathrm {a}} \ left（\ omega \ right）\ times {I} _ {\ mathrm {s}} \ left（\ omega \右）$$（4）$$ T \ left（\ omega \ right）=1-I \ left（\ omega \ right）$$（5）

省エネの要件を満たすために、 a 1より大きくすることはできません。 W _a およびω _a 中心周波数と帯域幅から計算できます[15、16]。非対称パラメータ q 変調減衰パラメータ b [16]で与えられた方法で得ることができます。このようにして、この非対称構造の理論的な透過スペクトルを得ることができます。図2fで、黒い曲線はFDTD法によって与えられた透過スペクトルを表し、赤い曲線はファノ共鳴の電磁理論に基づいた計算結果を示しています。黒と赤の曲線の一貫した傾向は、共振器の透過特性を明るいモードと暗いモードの結合に帰することが合理的であることを示しています。この結論は、図3の電界の分布とも一致します。

幾何学的パラメータ d ストリップ2の軸と構造全体の中心点との間の距離を表します（図1c）。これは、透過ディップの中心周波数とその透過係数に大きな影響を与える可能性があります。異なる d の対応する透過スペクトル 図2dに示されています。黒の曲線と赤の曲線は、それぞれシミュレーションと理論計算に基づく透過スペクトルを表しています。 d を使用 10μmから30μmに変化すると、明るいモードと暗いモードの間の結合強度の増加に起因して、鋭いファノディップが深くなることが明らかです。さらに、モード R の中心周波数 _d ストリップ2をストリップ1の近くに配置すると、明確な青方偏移が存在します。LC回路モデルに基づくと、 R の共振周波数 _d [45]によって与えられます。

$$ {\ omega} _ {\ mathrm {d}} =\ frac {1} {2 \ uppi \ sqrt {\ mathrm {LC} / 2}} \ propto \ frac {1} {\ mathrm {l}} $$（6）

ここで l 対応する共振器の等価長です。式（6）は、中心周波数ω _d l に反比例します 。私たちの構造では、同等の長さ l 図1cでは一点鎖線の長さで示されています。これは、 R のフィールド分布が原因です。 _d 主にストリップ1と2に制限されます。ストリップ1（と2）の長さと、2つのストリップ間の距離が lを決定します。 d のとき 増加すると、2つのストリップ間の距離が減少します。したがって、図1cに示すように、 d の場合、等価長は減少します。 10から30μmに変化します。これにより、 R が増加します。 _d の共振周波数。

1961年にファノによって提案されたファノ共鳴の理論[12]によれば、自動イオン化のプロセスが研究され、共鳴の非対称の線形状は、連続体と離散状態の間の干渉に起因します。これは、この論文で提示されたメタマテリアル共振器の非対称特性の起源でもあります。図4に示すように、構造の遷移メカニズムを明らかにするために3レベルのシステムを利用できます。 R ₀ システム全体の基底状態として機能します。ブライトモード R ₁ は、垂直入射ビームによって直接励起できる放射モードです。このシステムでは、非放射状態 R ₂ 前述のように、「ダークモード」[21]と見なすことができます。 R ₂ 対称性の破れによって興奮することができます。非対称性を導入すると、明るいモードと暗いモードを結合できるチャネルが提供されるため、ファノ共鳴が発生します[46]。

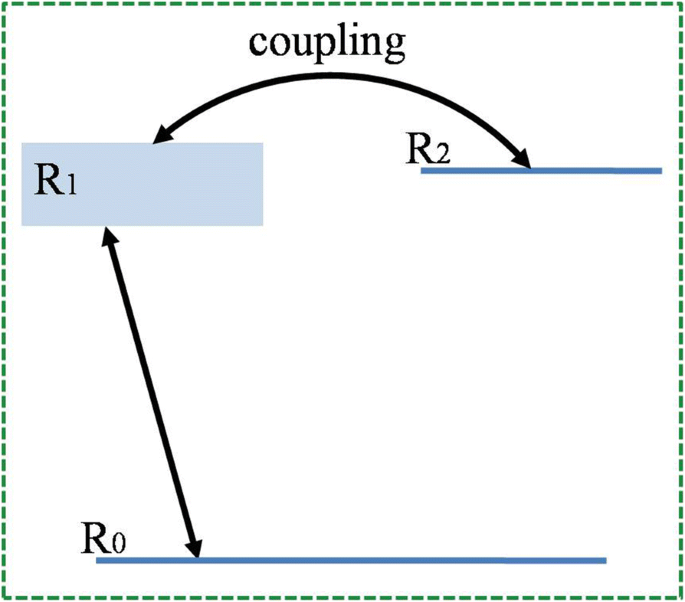
3レベルシステムの概略図

入射電磁波と分析物層の間の強い相互作用により、 Q が高くなります。 屈折率の超高感度検出を実現する有望な方法であるファノ共鳴 n [8]。図5aで提案されているデバイスは、屈折率 n を検出するための効果的なセンサーとして機能できます。 厚さが4μmの上部の分析物層の。伏角の中心周波数は n の変化に伴って変化します 。したがって、 R の共振周波数を分析することにより、屈折率を得ることができます。 _d 。図5bは、デバイス内のFanodipの共振周波数のシフトを示しています。 n の場合、明確な赤方偏移が表示されます 1から1.6に増加します。センシング感度 S \（\ frac {\ varDelta f} {\ varDelta n} \）と等しい。ここで、 S センサーの屈折率は0.105THz / RIU（屈折率単位）と計算されます。 FOM（性能指数）がセンサーの性能の重要な基準であることはよく知られています[47]。 FOM =\（\ frac {S} {\ mathrm {linewidth}} \）で計算できます。この提示された構造では、FOM値は7.501に達する可能性があり、これは理想的なレベルです[47、48]。センシング機能は通常、FOM * =\（\ frac {S ^ {\ ast}} {I} \）およびS * =\（\ frac {\ varDelta I} {\ varDelta n} \）によっても説明されます。検出された強度に関連しています。この構造でのS *の計算結果は2.6 / RIUです。また、構造内のFOM *は10と計算されます。また、分析物層の厚さによる応答の変化を把握するためにいくつかの作業を行いました。追加ファイル1を参照してください。

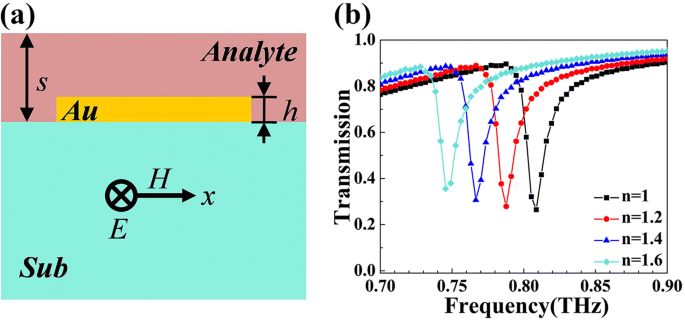
a センシングデバイスの断面。 b 屈折率の変化に対する透過スペクトルの依存性 n

複数のファノ共鳴は、多くの状況で応用できる可能性があります。ただし、ほとんどのプラズモンファノメタマテリアルは、単一のファノ共鳴をサポートするように設計されています[11、17]。そのため、構造を調整することで複数のファノ共鳴を実現することは容易ではありません。この論文では、メタマテリアルの元の設計に水平方向のストリップを追加することで、複数のファノ共鳴を実現します。代表的な例として、5ストリップ構造を示します。 5ストリップ共振器の概略図を図6aに示します。ストリップ1、2、3、および4は同じサイズで、互いに平行です。それらの長さは l _x =120μm、幅は w =20μm。ストリップ3は中央にあり、距離は d ストリップ2とストリップ3の軸の間は32μmです。ストリップ5は、他の4つのストリップに垂直です。その長さは l _y =150μm、幅は w =20μm。境界条件とメッシュサイズは、4ストリップ共振器のシミュレーションと同じに保たれます。シミュレーション結果を図6bに示します。この図では、0.75THzと0.91THzで2つの鋭いファノディップがはっきりとわかります。 Q これらの2つのディップの値はそれぞれ61と65です。構造に水平方向のストリップを追加すると、ファノディップをさらに生成する必要があります。

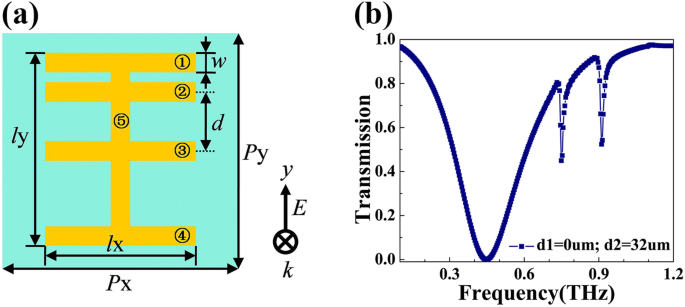
a 提案された5ストリップ構造の上面図。 b 5ストリップ共振器のシミュレートされた透過率曲線