有限要素引き裂きおよび相互接続法によるナノスケールでの光トラッピングの効率的な予測と分析

はじめに

表面プラズモン（SP）に基づくプラズモニック光ピンセットは多くの注目を集めており、ナノ粒子の捕捉に広く適用されています[1,2,3,4,5,6]。 SPは、金属と誘電体の界面での特定の波長と自由電子との入射光の結合によって引き起こされる共鳴現象です[7]。 SPを使用すると、光ピンセットが回折限界を突破できます。さらに、SPの劇的な局所場増強は、入射光の強度の要求を減らすことができます[7、8]。ただし、SPは物体の材質や寸法、入射光の波長と密接に関係しているため、実際にSP光ピンセットの最適なパラメータを決定するには多くの実験が必要です。これに基づいて、シミュレーション方法は、SP光ピンセットの設計と最適化の補助手段としてますます重要な役割を果たします[9]。これらのシミュレーションでは、安定したトラッピングを予測するために光学力の計算が必要です。球などの通常のオブジェクトの場合、光学力は一般化されたLorenz-Mie理論から解析的に導き出すことができます[10、11]。ただし、複雑な構成のオブジェクトの場合、電磁場とそれに続く光学力およびポテンシャルをモデル化するには、支配的なマクスウェルの方程式を厳密に解く数値的手法が必要です。

これらの数値解法は、主に微分方程式法（DEM）と積分方程式法（IEM）に分類できます[12、13、14、15]。 IEMと比較して、微分方程式法（DEM）は、複雑な形状やコンポーネントを処理する上で優れた能力を示します。 DEMには、SPの分析で重要な役割を果たす近接場分布を簡単に計算できるという利点もあります。代表的なDEMとして、有限差分時間領域（FDTD）法が時間領域に実装されており、ブロードバンド情報と過渡応答を簡単に取得できます[16、17]。ただし、FDTDは、SPの周波数依存材料特性を記述するための正確な分散モデルを必要としますが、FDTDソリューションの精度は、この分散モデルの近似精度に大きく依存します[18]。さらに、FDTDは構造化メッシュに依存しているため、曲面の階段エラーが発生することがよくあります。もう1つの代表的なDEMとして、有限要素法（FEM）が広く採用されています。これは、周波数領域で分散材料を簡単に処理でき、非構造メッシュによる階段誤差を排除できるためです[19、20、21、22]。 FDTDと比較すると、FEMは、近似分散モデルなしで、測定された材料パラメータを直接採用できます。ただし、SPでの大幅なローカルフィールドの拡張には、FEM離散化での細かいメッシュが必要です。その上、大きな次元と複数のオブジェクトを持つオブジェクトは、未知数の数を劇的に増やします。これらの要因は、悪条件のマトリックスシステムと膨大な計算量の消費を引き起こし、SPで強化された光トラッピングの分析のための従来のFEMに大きな課題をもたらします。

この記事では、ナノスケールでの光トラッピングをシミュレートするために、効率的なデュアルプライム有限要​​素引き裂きおよび相互接続（FETI-DP）法を紹介します。 FETI-DPは、元の大規模な複雑な問題を一連の小規模な単純な問題に分割してそれらを克服する、重複しない領域分割スキームを採用しています。サブドメインインターフェイスで送信条件を適用して、フィールドの連続性を確保し、デュアル変数を導入して、元の3次元（3D）問題をラグランジュ乗数による2次元（2D）問題に減らします。双対問題の反復解の収束率を加速するために、サブドメインコーナーの主変数が抽出されます[23、24、25、26]。 FETI-DPのパフォーマンスを向上させるために、低ランクのスパース化アプローチが開発されています。データスパースアルゴリズムを使用して、サブドメイン問題と双対問題を解決するための効率を向上させます[27、28]。提案された方法は、完全に分離されたサブドメインを提供し、ナノ粒子をトラップするための光学力の並列シミュレーションを可能にします。電磁場と機械的運動量の関係を明らかにするマクスウェル応力テンソル（MST）を採用して、光学力を評価します[29]。得られた光学力に基づいて、安定したトラッピングの分析のために光学ポテンシャルをさらに計算することができます。 IEMと比較して、提案された方法は、複合材料を処理し、SPベースの光トラッピングの近接場を解決する上でより強力です。 FDTDと比較して、提案された方法は、SPベースの光トラップシステムで分散金属材料を正確に処理し、曲線境界を持つオブジェクトの階段誤差を排除することができます。提案手法はFEMと比較して、光トラッピングの大規模計算に適しています。いくつかの例が分析され、数値結果は、ナノスケールでの光トラッピングの予測と分析のために提案された方法の精度と効率を示しています。

メソッド

FETI-DPの定式化

FETI-DP実装の場合、元の計算ドメインΩは最初に一連の重複しないサブドメインΩ ^{i に引き裂かれます。} （ i =1、2、3⋯、 N _s ）、図1に示すように。各サブドメインでΩ ⁱ 、サブドメイン有限要素システムは、ベクトル波動方程式から次のように導出できます。

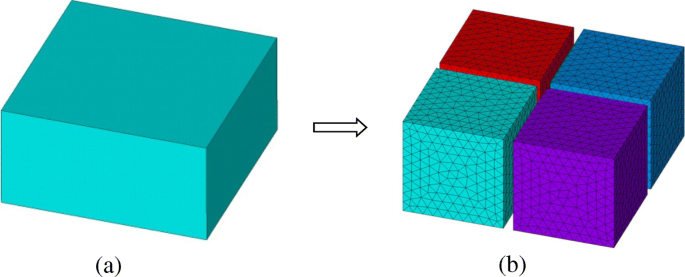
FETI-DP方式でサブドメインが重複しないドメイン分割スキーム。 a 元のドメイン。 b 分割されたサブドメインと離散化されたメッシュ

ここで E ⁱ \（{\ Omega} ^ i \）、 k で解かれる未知の電場を示します ₀ およびη ₀ はそれぞれ自由空間の波数と固有インピーダンスであり、\（{\ mathbf {J}} _ i ^ {\ mathrm {imp}} \）は印加電流です。 \（{\ Gamma} _ {\ mathrm {ABC}} ^ i \）は、無限の開いた領域を切り捨てるための吸収境界条件（ABC）を意味します。 k に注意する必要があります ₀ 周囲の媒体が自由空間でない場合は、媒体の波動インピーダンスに置き換える必要があります。これは、光トラッピングで一般的です。サブドメインインターフェースでΓ ⁱ 、Ω ^{i で完全な境界値問題を生成するには、仮定された境界条件が必要です。} 。ここで、未知の補助変数Λを持つロビンタイプの送信条件 _i として課せられる

ここで、\（{\ hat {n}} ^ i \）は、サブドメインインターフェイスΓ ^{i での単位法線外向きベクトルを示します。} 、およびα ⁱ は複雑なパラメータであり、多くの場合 jk として選択できます。 ₀ 。次に、すべてのサブドメインが四面体要素によって離散化されます。各要素で、 E を展開します ベクトル基底関数 N および未知の電界係数 E として

ここで s 各四面体要素のベクトル基底関数の数を示します。 s は、エッジに基づく従来の低次基底関数では6に選択されますが、面または体積に基づく追加の基底関数が導入されるため、高次ベクトル基底関数では大きくなります。

ガラーキン法を適用すると、Ω ^{i のFEM行列方程式} 未知の電界係数について E ⁱ として取得できます

ここで、添え字表記 c および r コーナー自由度（DOF）と残りのDOFを区別します。これにより、コーナーDOFがプライマリ変数として抽出され、デュアルプライマル（DP）スキームが構築されます。ここでは、 K はFEMシステムマトリックスであり、 f は励起ベクトルです。 B サブドメインのインターフェースDOFを抽出するブール行列です。 λ Λの展開から生成される二重変数です _i 、これはラグランジュ乗数とも呼ばれます。

次に、隣接するサブドメインは、界面で接線方向の電界と磁界の連続性を強制することによって相互接続できます。すべてのサブドメインインターフェースを組み立て、すべてのサブドメイン内部の未知数を排除します E ⁱ 。二重変数λに関する縮小グローバルインターフェース方程式 として取得できます

式（6）は、一般化最小残差（GMRES）法などの反復法によって解くことができます。 \（{\ tilde {\ mathbf {K}}} _ {cc} \）は、原始空間での反復収束を加速できるグローバルコーナーシステムです。適切な前処理行列を使用して、近似逆および不完全なLU分解などの反復収束率を向上させることができます。一度二重変数λ が解かれると、各サブドメイン内の電界は（5）によって独立して評価できます。グローバル行列\（{\ tilde {\ mathbf {K}}} _ {rr} \）を構築するには、サブドメインの数値グリーン関数\（{\ mathbf {Z}} _ {rr} ^を構築する必要があります。 i \）の形式で

ここで、サブドメインFEM行列の逆関数\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} ^ {-1} \）が含まれます。さらに、行列の場合\（{\ tilde {\ mathbf {K}}} _ {rc} \）、\（{\ tilde {\ mathbf {K}}} _ {cr} \）、および\（{\ tilde {\ mathbf {K}}} _ {cc} \）およびベクトル\（{\ tilde {f}} _ r \）および\（{\ tilde {f}} _ c \）、\（{\ left（{ \ mathbf {K}} _ {rr} ^ i \ right）} ^ {-1} \）を計算する必要があります。前処理段階での\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} ^ {-1} \）の構成と、それらの行列-ベクトル積（MVP）反復解法の段階では、計算コストが高くなります。 \（{\ mathbf {K}} _ {rr} ^ i \）はまばらですが、\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} ^ {-1} \ ）密度が高いため、計算コストが高くなります。次に、\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} ^ {-1} \）の計算を高速化するために、低ランクのスパース化メソッドが導入されます。グローバルインターフェースシステムの一部の部分行列は低ランク行列形式で表すことができるため、それらの計算は低ランクアルゴリズムで実行でき、FETI-DPのパフォーマンスが向上します。 FETI-DPは独立したサブドメイン操作を提供するため、並列計算を活用して効率を向上させることができます。効率的な並列スキームの場合、ドメイン分割の原則は、各サブドメインのDOFの数を可能な限りバランスさせることです。したがって、サブドメインのサイズはメッシュの離散化密度に関連している必要があります。通常、小さなサブドメインは細かいメッシュの領域で採用され、大きなサブドメインは粗いメッシュの領域で採用されます。

低ランクのスパース化

FETI-DPの効率を改善するためのデータスパースな方法を提供するために、低ランクのスパース化アプローチが提案されています。ここでは、データスパース つまり、これらの行列は実際にはスパースではありませんが、それらの特定のサブブロックを低ランクの分解行列形式で表すことができるという意味でスパースです。

ここで、 X および Y 完全な行列形式であり、ランク k m よりはるかに小さい および n 。行列\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} ^ {-1} \）は、積分の行列プロパティを持っているため、データスパース行列形式で表すことができます。オペレーター。したがって、\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} ^ {-1} \）が特定のサブドメインで低ランクのプロパティを持っている場合、効率的に計算して次の場所に格納できます。反復ソリューションでMVPを高速化する、低ランクのスパース化アプローチを使用したデータスパースフォーム。

低ランクスパース化アプローチのプロセスは、次のステップに分けることができます。（1）各サブドメインに設定された基本関数を細分化してクラスターツリーを構築する、（2）2つのクラスターツリーの相互作用によってブロッククラスターツリーを構築する、（ 3）許容条件によって\（{\ mathbf {K}} _ {rr} ^ i \）のデータスパース形式を生成します。（4）低ランク形式のアルゴリズムを実行して\（のデータスパース表現を取得します。 {\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} ^ {-1} \）、および（5）次の方法でFETI-DPシステムの解を入力します。データスパースアルゴリズム。適切な前処理行列を使用して、ソリューションを高速化できます。データスパースLU分解\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} ={\ left（{\ mathbf {L}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} {\ left（{\ mathbf {U}} _ {rr} ^ i \ right）} _ {\ mathrm {DS} } \）は、行列の反転\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} ^ {-1} \）の代わりに採用されます。ネストされた解剖技術は、低ランクのスパース化の効率をさらに改善するために採用されています。ネストされた解剖では、セパレータを使用して大きな非対角のゼロサブブロックを生成します。これにより、LU分解中にゼロが維持されるため、フィルインを大幅に削減できます。

\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} \）を生成するには、最初にクラスターツリー T を構築します。 _私 サブドメインエッジベースの基底関数セット I の再帰的細分割による ={1,2、…… N }バウンディングボックスを使用します。ネストされた解剖では、クラスター t 対応するバウンディングボックス内で、3つの後続{ s ₁ 、 s _9月 、 s ₂ }、ここで s ₁ および s ₂ は、2つの切断されたバウンディングボックスと s のインデックスセットです。 _9月 セパレータのインデックスセットです。図2aは、このプロセスの簡単な例を示しています。次に、ブロッククラスターツリー T _{私 ×私} 2つのクラスターツリー T を相互作用させることで構築できます _私 、図2 bに示すように、これは、元のエッジベースの基底関数セットとガラーキン法で設定されたテスト基底関数のクラスターツリーとして選択できます。次に、ネストされた解剖に基づく許容条件を導入して、 T の完全なブロック、低ランクの分解ブロック、および非対角のゼロブロックを区別する必要があります。 _{私 ×私} [23]。したがって、\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} \）は、対応するブロックにゼロ以外のエントリを入力することで生成できます。 \（{\ mathbf {K}} _ {rr} ^ i \）。最後に、\（{\ left（{\ mathbf {K}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} ={\ left（{\ mathbf {L }} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} {\ left（{\ mathbf {U}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} \ ）から再帰的に計算できます

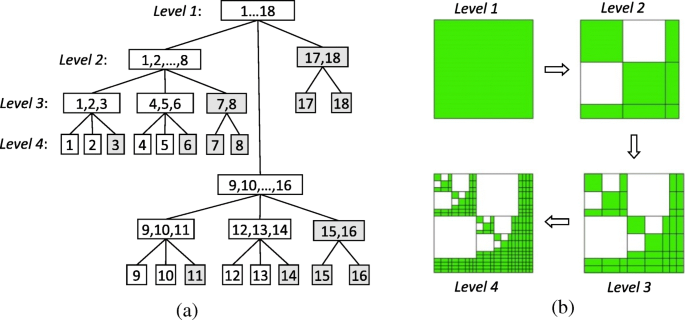
ネストされた解剖に基づく4レベルのクラスターツリーとブロッククラスターツリーの構築。 a エッジベースの基底関数セット I の再帰的細分割によるクラスターツリーの構築 ={1,2、…18}。 b 白のブロッククラスターツリーの構築 ブロックはゼロ行列であり、緑 ブロックは、完全行列または低ランク分解行列にすることができます

ここで、従来の完全行列演算は、データが少ない対応する演算に置き換えられます[28]。適応打ち切り誤差ε _t 低ランク近似の精度を制御するために使用されます。得られたLU係数\（{\ left（{\ mathbf {L}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} \）および\（{\ left（{\ mathbf {U} } _ {rr} ^ i \ right）} _ {\ mathrm {DS}} \）が保存され、

ここで、\（{\ mathbf {B}} _ r ^ i {\ left（{\ mathbf {U}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} ^ {-1} \）および\（{\ left（{\ mathbf {L}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} ^ {-1} {\ mathbf {B}} _ r ^ i \）データスパース上三角ソルバーと下三角ソルバーによって計算されます。 \（{\ left（{\ mathbf {L}} _ {rr} ^ i \ right）} _ {\ mathrm {DS}} \）、\（{\ left（{\ mathbf {U}} _ { rr} ^ i \ right）} _ {\ mathrm {DS}} \）、および\（{\ mathbf {Z}} _ {rr} ^ i \）は、データがスパースな前方および後方でFETI-DP計算を入力します置換（FBS）とデータスパースMVP。

光学力とポテンシャル

電気力学理論によれば、光力は、電磁場と機械的運動量の関係を明らかにするマクスウェル応力テンソル（MST）によって評価できます[29]。対象物の周囲の電磁界分布が得られたら、対象物を取り巻く閉じた表面上でMSTを積分することにより、光学力を計算できます。得られた電界分布に基づいて、任意の座標でのMSTを作成できます

ここで、上付き文字のアスタリスクは、電場または磁場の共役εを示します。 μです は誘電率と透磁率であり、\（\ overleftrightarrow {\ mathbf {I}} \）は3×3単位行列です。ベクトルの外積により、\（\ overleftrightarrow {\ mathbf {T}} \）のテンソル形式は

ここで、下付き文字 x 、 y 、 z 3方向のコンポーネントを示します。 E の拡大によると （4）で説明されている、MST T のエントリ _mn （ m 、 n = x 、 y 、 z ）は、FETI-DP計算で次のように拡張形式に変換できます

ここでω 角周波数です。 N および s 式で説明されています。 （4）。

最後に、オブジェクトに作用する光学力は、オブジェクトを囲む閉じた表面上でMSTを積分することによって計算できます

MSTの積分は対応するサブドメインに割り当てられているため、光学力の計算も並行して実行できることに注意してください。安定した光トラッピングの場合、主な条件の1つは、勾配力が散乱力よりも大きくなければならないことです。つまり、全力の方向は勾配力の方向と同じである必要があります。勾配力は、常に電界強度が最も強い位置を指します。

光ポテンシャルは、光トラップの安定性を明らかにするもう1つの魅力的なパラメータです。得られた光学力に基づいて、光学ポテンシャルの深さ U 位置 r ₀ によって計算することができます

ここで、下付き文字∞は、電位がゼロの基準点として定義された無限大を示します。 U の値 k で表すことができます _B T、ここで k _B 1.3806488×10 ⁻²³ のボルツマン定数を示します J / KおよびTは周囲温度です。一般に、粒子は溶液中のブラウン運動に打ち勝ち、 U のときに安定してトラップされます。> 1 k _B Tは満足しています。そうしないと、粒子を安定してトラップできません。総光学力には保存力勾配力成分と非保存散乱力成分が含まれるため、総光学力 F （15）からは非保守的です[30、31]。ただし、ナノ粒子の運動が1次元に制限されている場合、総光学力は保存的ではありませんが、これにより（16）からの光学ポテンシャルの明確な定義が得られます。

結果と考察

提案された方法の有効性を実証するために、3つの例が提示されます。表面プラズモンを励起するために貴金属が一般的に使用されるため、分析には代表的な金と銀の材料を選択します。最初の例では、銀ナノ粒子の光学力を計算して、提案された方法の精度を検証します。 2番目と3番目の例では、金ナノ粒子の光トラップをシミュレートして説明します。すべての例で、無限領域はABCで切り捨てられ、ABCとオブジェクト間の距離は1波長に設定されています。これは、許容可能な精度を達成するのに十分です。すべての計算は、3.6GHzのIntelXeonプロセッサを搭載したDellワークステーションで実行されます。

シルバーナノカプセル

銀ナノカプセルオブジェクトは、光学力を予測する際に提案されたFETI-DP法の精度と効率をテストするために最初に考慮されます。図3aおよびbは、その構成と寸法を示しています。銀の構成パラメータはすべて[32]から取得した測定値です。 FETI-DPスキームを実装するために、分析ドメイン全体が最初に24のサブドメインに分割されます。プラズモン局所場増強効果をモデル化するために、金属表面の近くに高密度メッシュが必要です。離散化には四面体要素が採用されており、全体で6.9×10 ⁵ になります。 4.1×10 ⁴ を含む不明 デュアル未知数と313コーナー未知数。入射光は+ z の方向に沿って点灯します 、電界の分極方向は- x です。 。

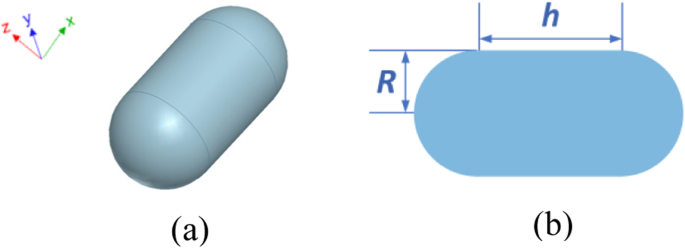
銀ナノカプセル構造の構成。 a 3Dビュー。 b 正面図と寸法、ここで R =30nmおよび h =60 nm

まず、入射光の波長を変更しますλ ナノカプセルに加えられる光学力をシミュレートするために200nmから400nmまで。 FETI-DPは周波数領域で動作するため、光学力は15のサンプリング周波数ポイントで計算されます。図4は、銀ナノカプセルに加えられる光学力の計算された曲線を示しています。 FETI-DPの精度を示すために、FETI-DPの光学力の結果を商用ソフトウェアのLumerical FDTD Solutions [33]の結果と比較すると、良好な一致が見られます。

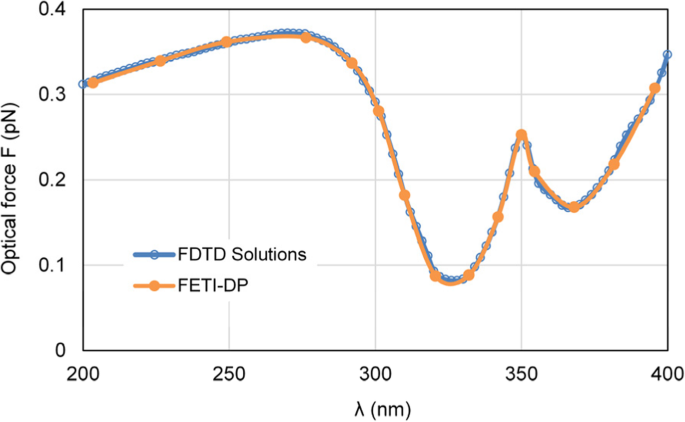
銀ナノカプセルに加えられた光学力の結果。波長λによって異なります。 FETI-DPおよび商用ソフトウェアFDTDソリューションの結果を含む入射光の分析

次に、FETI-DPのパフォーマンスが、さまざまな数のサブドメインについてテストされます。離散化密度を維持することにより、サブドメインの数を4から24に増やします。各プロセッサに1つのサブドメインを処理するように割り当てます。表1は、グローバルインターフェイスの構築に使用された時間を示しています。 （6）および合計ソリューション時間。 FETI-DPは、並列コンピューティングリソースを十分に活用し、ソリューションの効率を大幅に向上させることができます。さらに、サブドメインの数が増加するFETI-DPの精度も調べて、表1に報告します。ここで、精度は、光学力の2ノルム相対誤差によってδとして定義されます。 _OF =‖ OF _i − OF _ref ‖/‖ OF _ref ‖、ここで OF _i i を使用した光学力です サブドメインと OF _ref 2つのサブドメインを使用した参照光学力を示します。サブドメインの数が増えても、精度はほぼ一定に保たれていることがわかります。

ゴールドナノスフィアダイマー

2番目の例では、金ナノスフェアダイマーを使用して金ナノスフェアの光トラッピングを分析します。二量体ギャップでのプラズモン効果は、ナノ粒子をトラップするための光学力を効果的に高めることができます。図5aおよびbは、このシステムの構成と寸法を示しています。金の構成パラメータはすべて[32]から取得した測定値です。周囲の媒体は、相対屈折率が n の水です。 =1.33。入射光は、10mW /μm ² のパワーを持つ平面波です。 、電界分極方向は+ x 、および入射方向は- z 。対象物のナノスフェアにかかる光学力は、FETI-DP法により計算されます。 FETI-DP実装の場合、計算ドメイン全体が32のサブドメインに分割され、四面体メッシュによって離散化されます。これにより、3.5×10 ⁶ になります。 1.6×10 ⁵ を含む不明 二重未知数と1738コーナー未知数。

水中の金ナノスフィア二量体の光トラップシステムの構成。 a 3Dビュー。 b 正面図と寸法、ここで R =25 nm、 r =5 nm、および g =2 nm

まず、さまざまな数のプロセッサを使用して、提案されたFETI-DPの並列パフォーマンスをテストします。表2は、式（1）の解の時間を示しています。 （6）および総解決時間。さらに、並列計算のスピードアップも表2に示されています。ここで、スピードアップは次のように定義されます。

ここで、\（{T} _ {N_p} \）は、 N を使用した実時間の合計を示します。 _p プロセッサ。 FETI-DPはソリューション効率を大幅に改善し、優れた並列スピードアップを示すことがわかります。この多数の未知数の場合、すべてのプロセッサの合計メモリ使用量はわずか57.2GBです。

次に、低ランクのスパース化アプローチの有効性を調べます。低ランクのスパース化では、サブドメイン行列をデータスパースアルゴリズムで因数分解し、データスパース行列として保存できます。構築時間とメモリ使用量はわずか18秒と0.5GBですが、従来のマトリックスアルゴリズムでは67秒と1.7GBです。 72％の時間節約と70％のメモリ圧縮が得られることがわかります。メモリ使用量に関連して、後続のMVPも70％の時間を節約できます。

次に、FETI-DPは、波長λでの光学力計算のためにテストされます。 277nmから818nmまで変化します。実際には、異なる波長の入射光の下での光学力の分析は、プラズモン共鳴波長を検索するためにしばしば必要であり、そこでは劇的な場の増強が起こり、最も強い光学力を得ることができる。ナノスフェアが（0、0、20 nm）と（0、0、− 20 nm）にある場合の2つのケースが考えられます。図6aおよびbは、さまざまなλに対してナノスフェアに加えられた計算された光学力をプロットしています。 。最大光学力はλで発生することがわかります。 =472 nm、これはプラズモン共鳴波長です。この共鳴波長での光学力は、非共鳴波長での光学力に比べて約40倍向上しました。また、電界強度が最も強い図6に示すように、光学力は常に二量体ギャップを指します。これは、オブジェクトをトラップする勾配力の方向でもあります。図7aおよびbは、λの非共鳴波長で計算された電界増強分布を示しています。 =300nmおよびλの共鳴波長 それぞれ=472nm。プラズモン共鳴効果により、電界強度が約250倍に増加していることがわかります。

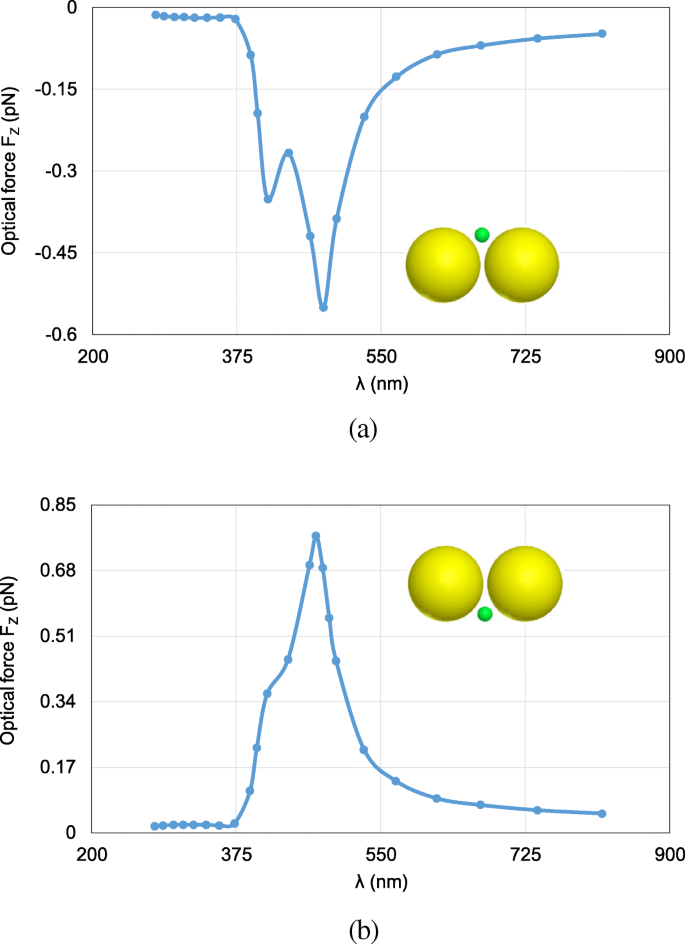
金ナノスフィア二量体のシステムでナノスフィアに加えられた光学力の計算結果。波長λによって変化します。 入射光の。 a オブジェクトのナノスフェアは（0、0、20 nm）にあります。 b オブジェクトナノスフェアは（0、0、− 20 nm）にあります

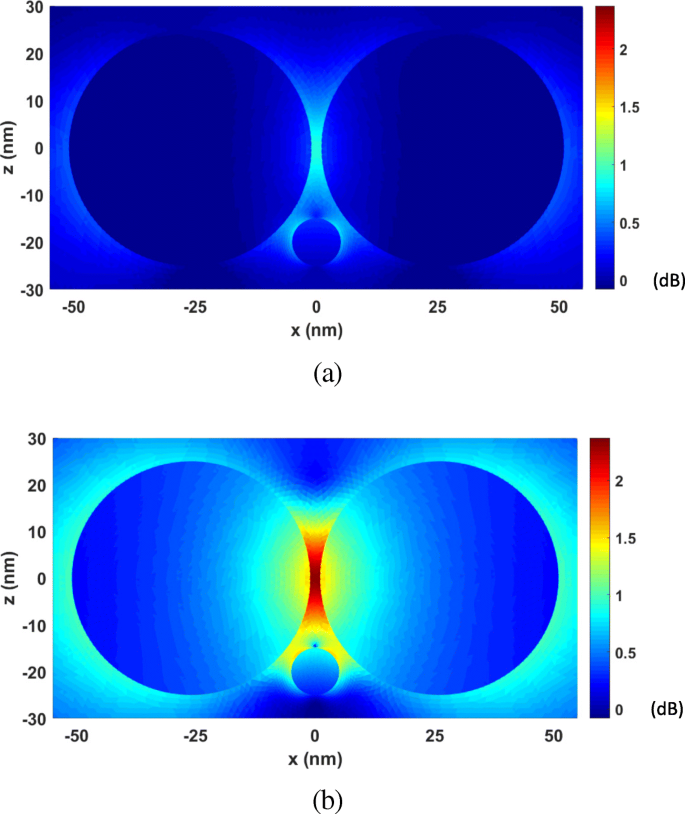
xoz の電界増強分布 金ナノスフェア二量体のシステムの平面。 a λ =300 nm（非共振波長）。 b λ =472 nm（共振波長）

さらに、光学力と光学ポテンシャルは、ナノスフェアが z に沿って（0、0、− 30 nm）から（0、0、− 17 nm）に移動することで計算されます。 -軸。トラップ力とポテンシャルの最も典型的で興味深い振る舞いは、 z に沿って作用するものです。 -方向、ここでは z に沿った積分による軸方向のトラップの可能性を検討します -軸。ナノ粒子の運動は一次元に制限されているため、（15）からの総光学力は非保存的ですが、光学ポテンシャルの定義は（16）から明確です。図8a、bに示すように、ナノスフェアが二量体ギャップに移動すると、光学力と光学ポテンシャルの深さが明らかに増加します。 （0、0、− 17 nm）の位置で、4.6 k の光学ポテンシャルの深さ _B Tが生成されます。これは、水中でのブラウン運動を克服して安定した光トラップを実現するのに十分です。

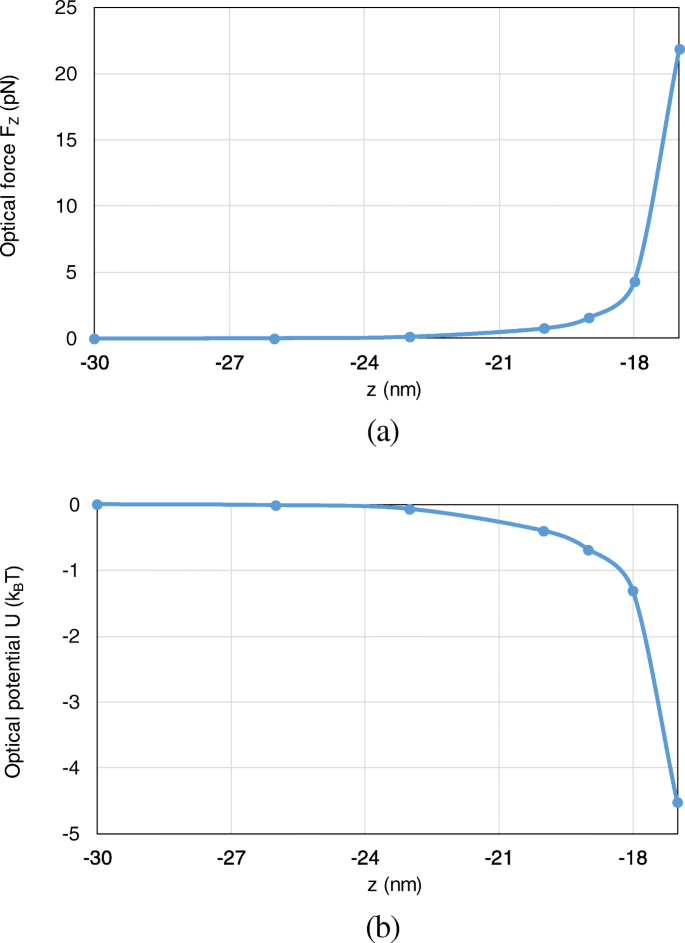
ナノスフィアが（0、0、− 30 nm）から（0、0、− 17 nm）に移動するときに、金ナノスフィア二量体のシステムでナノスフィアに作用する光学力と光学ポテンシャル。 a 光学力。 b 光学ポテンシャル

最後に、この例の誘電体基板の効果をテストします。光学力は、基板がある場合とない場合でそれぞれ計算されます。どちらの場合も、ナノスフェアは（0、0、− 20 nm）に位置し、入射波長が共鳴波長として選択されます。基板がない場合、光学力の計算結果は| F です。 ₀ | =0.769pN。基板の場合、金ナノスフェアダイマーは、厚さ60 nm、比誘電率εの誘電体基板上に配置されます。 _r =2.25。光学力の計算結果は| F です。 ₁ | =0.761pN。これら2つの光学力の結果の相対誤差は、約1.0×10 ^-2 です。 、これは| F として定義されます ₁ − F ₀ | / | F ₀ |。

ゴールドの円錐台ダイマー

3番目の例では、金の円錐台二量体を使用した金ナノスフェアの光トラップを扱います。図9に、このシステムの構成と寸法を示します。金の構成パラメータは[32]から取得されます。誘電体基板の比誘電率はεです。 _r =2.25。周囲の媒体は、相対屈折率が n の水です。 =1.33。入射光は10mW /μm ² のパワーの平面波です。 、電界分極方向は+ x 、および入射方向は- z 。計算ドメイン全体が32のサブドメインに分割され、四面体メッシュによって離散化されます。これにより、3.1×10 ⁶ になります。 1.3×10 ⁵ を含む不明 二重未知数と1227コーナー未知数。

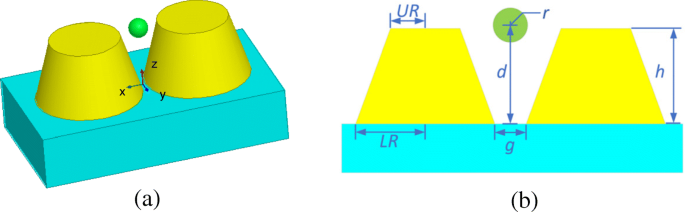
水中の誘電体基板に基づく金の円錐台二量体の光トラップシステムの構成。 a 3Dビュー。 b 正面図と寸法、ここで UR =20 nm、 LR =30 nm、 h =35 nm、および g =2 nm

まず、λを変えて光学力を解析します。 277nmから818nmまで。図10は、さまざまなλに対してナノスフェアに加えられた計算された光学力をプロットしたものです。 。ナノスフェアは（0、0、35 nm）にあります。最大光学力はλで発生することがわかります。 =464 nmはプラズモン共鳴波長であり、ここでの光学力は非共鳴波長で約30倍に増強されます。さらに、総光学力は常に- z を指します 、図10に示すように、勾配力の方向です。これは、勾配力が散乱力よりも大きいことを確認します。これは、ナノスフェアを安定してトラップできる条件の1つです。図11aおよびbは、λの非共鳴波長で計算された電界分布を示しています。 =300nmおよびλの共振波長 それぞれ=464nm。局在表面プラズモン共鳴により、電界強度が約500倍に増加していることがわかります。

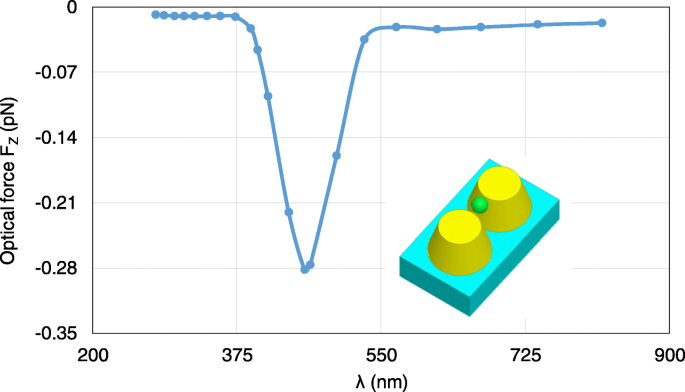
λによって変化する、金の円錐台二量体のシステムでナノスフェアに加えられた光学力の計算結果 。ナノスフェアは（0、0、35 nm）にあります

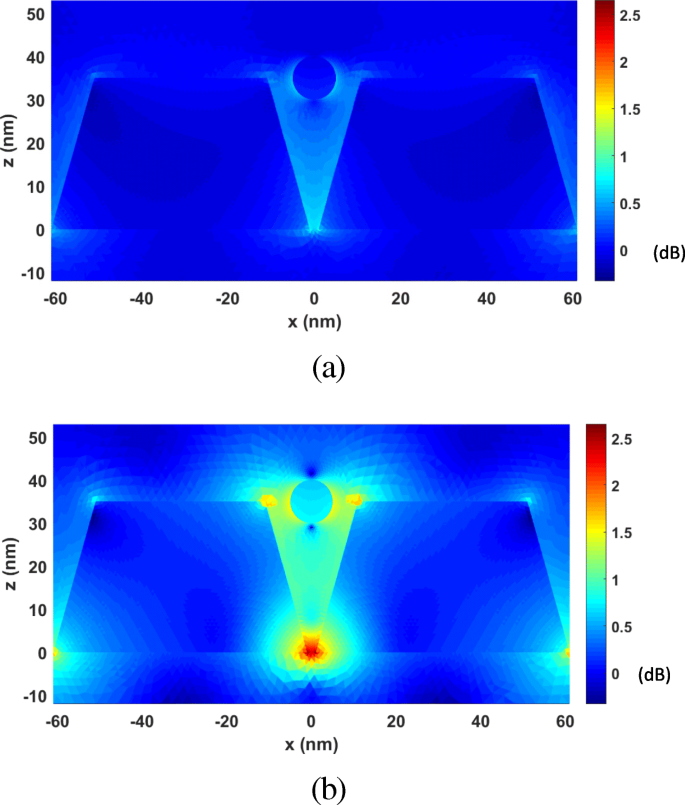
xoz の電界増強分布 金の円錐台二量体のシステムの平面。 a λ =300 nm（非共振波長）。 b λ =464 nm（共振波長）

次に、ナノスフェアの位置を0、5、および35 nmに変更して、光学力を観察します。図12は、ナノスフェアに加えられた計算された光学力を示しています。ここで、明らかな y - z が大きい間、光学力の成分を観察できます -光学力の成分が存在します。総光学力は、依然として、ナノスフェアをトラップするための最も強い電場のある位置を指しています。

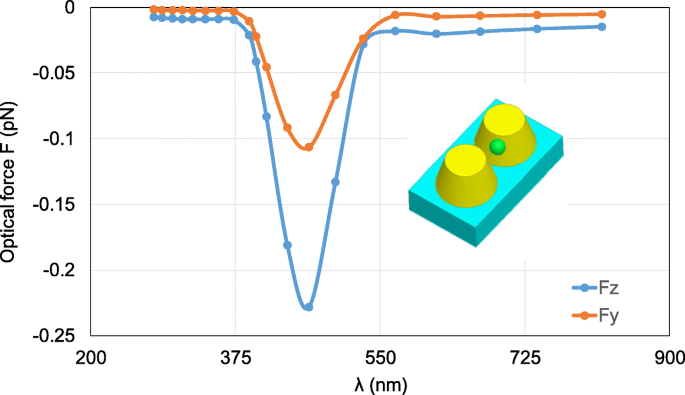
λが変化する金の円錐台二量体のシステムでナノスフェアに加えられた光学力の計算結果 。ナノスフェアは（0、5 nm、35 nm）にあります

さらに、 z に沿ってナノスフェアが（0、0、50 nm）から（0、0、20 nm）に移動するときの光学ポテンシャルを分析します。 -軸。ここでは、 z に沿った軸方向のトラップポテンシャルを検討します。 -方向。ナノ粒子の動きを1次元に制限し、光学ポテンシャルの明確な定義につながります。光学力と電位の両方が計算されます。図13a、bからわかるように、ナノスフェアが二量体ギャップに移動すると、光学力と光学ポテンシャルの深さが明らかに増加します。 （0、0、20 nm）で、3.8 k の光学ポテンシャルの深さ _B 安定した光トラッピングを実現するために水中でのブラウン運動を克服するのに十分なTが得られます。

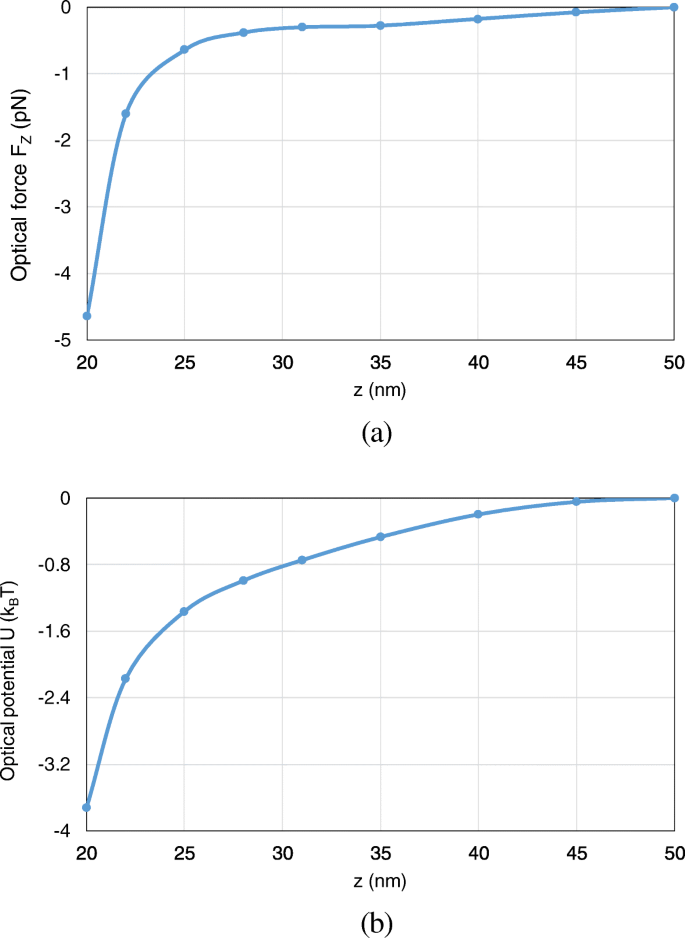
ナノスフェアが（0、0、50 nm）から（0、0、20 nm）に移動するときに、金の円錐台二量体のシステムでナノスフェアに作用する光学力と光学ポテンシャル。 a 光学力。 b 光学ポテンシャル

最後に、メッシュサイズの違いに基づいて未知数の数を100万から320万に変更することにより、FETI-DPの計算コストをテストします。実際には、さまざまな精度要件を満たすには、通常、さまざまなメッシュ密度でのテストが必要です。このような大規模で複雑な問題は、従来の数値解法に大きな課題をもたらします。ただし、FETI-DPはこの問題を簡単に処理できます。 FETI-DPシミュレーションには32個のプロセッサが使用され、各プロセッサはサブドメインを処理します。表3に、FETI-DPの計算コストを示します。 FETI-DPは、高いシミュレーション効率と低いメモリ要件を示していることがわかります。

結論

金属ナノ粒子の光トラッピングの予測と分析のために、低ランクのスパース化と組み合わせたFETI-DP法が提案されています。提案された方法は、完全に分離されたサブドメイン問題を提供し、それは大規模な複雑な問題を一連の小規模な単純な問題に変換します。並列計算に最適で、数値シミュレーションの効率を大幅に向上させることができます。例は、提案された方法が大規模計算の優れた性能を示し、ナノスケールでの光トラッピングの高速で正確なシミュレーションに非常に適していることを示しています。

データと資料の可用性

この調査中に生成または分析されたすべてのデータは、この記事に含まれています。

略語

ABC：

吸収境界条件

DOF：

自由度

FDTD：

有限差分時間領域

FEM：

有限要素法

FETI-DP：

デュアルプライム有限要​​素の引き裂きと相互接続

MST：

マクスウェル応力テンソル

MVP：

行列-ベクトル積