ナノアンテナ粒子に基づくインテリジェントドラッグデリバリーシステムの新しい設計
要約
化合物ナノ粒子ドラッグデリバリーシステムは、リンパ節との相互作用において重要な役割を果たします。リンパ球には、B細胞、T細胞、ナチュラルキラー細胞の3つの主要なタイプがあります。免疫系の細胞が発がん性になると、体の細胞を攻撃します。リンパ液は、体の健康な細胞を攻撃する上で重要な役割を果たします。したがって、この論文は、感染した細胞を標的とするようにナノ粒子を効率的に誘導し、そのような細胞の高速除去を助けることができるドラッグデリバリーシステムを設計することを目的とした。提案された設計はこれらの分子間の相互作用に依存し、インテリジェントナノコントローラーは嫌気性接触によってナノ粒子を誘導する能力を持っています。提案された設計は、ナノ粒子のサイズと密度が小さいほど、液体の動的粘度が低くなることを証明しました。これは、流れに対する抵抗を反映しています。さらに、水素分子は密度が低いため、リンパ液の抵抗を減らすのに重要な役割を果たしていると結論付けられました。
はじめに
現在のがん治療の選択肢には、手術、放射線、化学療法などがあります。これらの治療戦略はまた、通常の組織に害を及ぼし、悪性腫瘍の部分的な消滅をもたらします。したがって、ナノテクノロジーは、有害な細胞や新生物を特異的に標的とし、腫瘍を直接切除し、放射線ベースおよびその他の治療法の有効性を高めることにより、これらの欠点を克服することができます。これにより、治療の副作用を大幅に減らし、生存率を高めることができます。ナノテクノロジーは、ナノ材料を使用することにより、より新しく、より優れた治療法を提供するため、悪性腫瘍の治療のための有望なツールです。ナノ粒子は、癌細胞で差次的に発現する多くの分子を特異的に標的にすることができます。ナノ粒子の一般的に広大な翼型領域は、小粒子やデオキシリボ核腐食性またはリボ核腐食性鎖ペプチド抗体などのリガンドで機能化することができます。リガンドは、薬物として、およびセラノスティックアプリケーションで使用されます。活力の注意散漫や再放射などのナノ粒子の物理的特性も同様に、レーザー脱毛や温熱療法の用途など、病気の組織に影響を与えるために使用できます[1]。
革新的なナノ粒子ソフトウェアプログラムと医薬品有効成分は、有効成分の幅広いレパートリーの探索も可能にします。したがって、免疫原性カーゴと表面コートは、ナノ粒子を介した化学療法と従来の化学療法の両方の補助剤として研究されています。この革新的な戦略には、細胞に提示する人工抗原としてのナノ粒子の設計と、抗腫瘍効果を発揮する刺激因子のinvivoデポが含まれます。ナノテクノロジーは、多くのアプリケーションで活発な研究分野を表しています。ナノ粒子は、解凍指数点、親水性、電気および熱伝導、触媒活性、光吸収、散乱などの調整可能な物理化学的特性により、医療技術に関心を集めています[2]。原則として、ナノ材料は1〜100nmの範囲の粒子を持つ材料として説明されます。欧州連合と米国には、ナノマテリアルを使用した医学研究に特に関連したいくつかの法律があります。しかし、国際的に認められているナノマテリアルの定義はありません。さまざまな組織がナノマテリアルのさまざまな概念を検討しています[3]。ナノ粒子ドラッグデリバリーシステムの目的の1つは、リンパ液を癌細胞で治療することです。リンパ節と相互作用する複合ナノ粒子ドラッグデリバリーシステムを図1に示します。
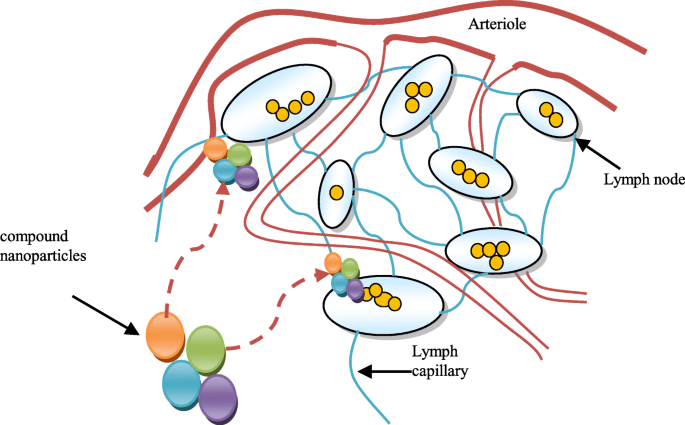
化合物ナノ粒子ドラッグデリバリーシステムとそのリンパ節との相互作用
米国食品医薬品局は、バルク材料とは異なる特性を持つ1〜100の範囲の粒子を持つ材料としてナノ材料をほのめかしています[4、5]。ナノファイバー、ナノプレート、ナノワイヤー、量子ドット、およびその他の関連材料が特徴づけられています[6]。固体脂質ナノ粒子(SLN)は、固体脂質を利用して構築できる脂質ナノ粒子(LN)の一種です[7]。ナノ構造脂質担体(NLC)などのSLNの後続バージョンが開発されており、これはLNの第2の時代を表しています[8]。 SLNとNLCはどちらも固体脂質から作られています。 SLNの内部構造には固体脂質が含まれていますが、NLCは固体脂質と液体脂質の混合物を利用して開発されており、宝石の断面を生成します[9、10]。これらの欠陥は、多くの固体脂質セグメントを含むSLNが医療用途で使用できるという事実に照らして、SLNについてさらに報告されています[11、12]。高分子ナノ粒子(PN)は、天然高分子または無機材料、たとえばシリカから構築できます[13]。ポリマーまたは脂質はNPのコアを形成し、安定性と薬物送達を改善し、均一な形状とサイズを提供します[14]。 PNは、ナノカプセルまたはナノスフェアとして説明できます。ナノカプセルは薬物とともに小胞構造の油を含み[15、16]、ナノスフェアは油を含まない高分子鎖を含みます[17、18]。薬物は、ポリマーとのブレンドによってPNに詰め込まれます。薬物の取り込みは、重合時にナノ粒子に確実に組み込まれます。 PNには、ポリマーネットワークの構成要素に薬物を溶解、散乱、または人工的に吸着させることにより、薬物がロードされます[19、20]。リンパ球には、B細胞、T細胞、ナチュラルキラー細胞の3種類があります。 B細胞は、侵入する微生物を攻撃する抗体を作りますが、発がん性になると免疫系も攻撃します。したがって、自己免疫におけるリンパ液の重要な役割を考慮して、この論文の目的は、ナノアンテナ粒子に基づくインテリジェントなドラッグデリバリーシステムを設計することでした。したがって、システムにはさまざまな量の多くのナノ粒子が含まれています。次のセクションでは、インテリジェントなドラッグデリバリーシステムの設計について説明します。
ナノインテリジェントドラッグデリバリーシステムの設計
提案されたナノインテリジェントドラッグデリバリーシステムは、ナノ圧電材料で作られたナノ粒子の電源によって操作されるナノコントローラーを含んでいます。ナノ粒子の複雑なリポジトリには、多数のマイクロリポジトリがあります。各小さなリポジトリには、1種類のナノ粒子が含まれています。ナノ粒子分子には、ナノコントローラーと通信するように設計されたナノアンテナが含まれています。提案されたナノインテリジェントドラッグデリバリーシステムには、癌細胞への薬物の迅速なデリバリーのためのカーボンナノチューブも含まれています。図2に示すように、感染した細胞と関連付けることができます。システムは、「探索的ナノ粒子」と呼ばれるナノ粒子を癌細胞に送ることから始まります。これらの分子は、嫌気性通信によって、細胞内の位置の全体像をナノコントローラーに送信します。探索的ナノ粒子が遭遇する状況に基づいて、ナノコントローラーは、探索的ナノ粒子から収集された情報に基づいて、異なる数、タイプ、および密度のナノ粒子を癌細胞に送信します。これらのナノ粒子は「ファイティングナノ粒子」と呼ばれます。
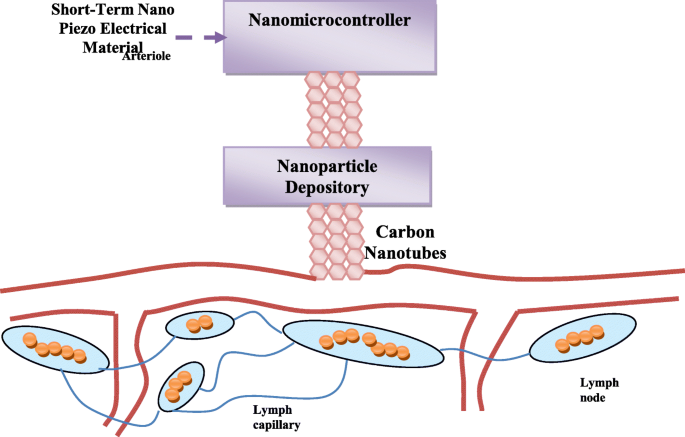
提案された薬物システムと感染細胞との関連を示す一般的な構造
これはランダムなプロセスではありませんが、ナノ粒子の効率的かつ迅速な送達を保証するいくつかの側面と対数を考慮して、ナノコントローラーによって制御されます。ナノ粒子を癌細胞に正確かつ迅速に送達するために、圧縮二分探索アルゴリズムが採用されます[21]。さらに、ナノ粒子は異なる密度で送達されるため、薬物はより効果的になります。ナノコントローラーを使用したこれらの方法論とその手口を図3に示します。ナノコントローラーの物理的構造はナノ粒子の物理的構造と似ていますが、電気エネルギーを得ることができるように金属の形をしています。作業中の短期間。この金属には、ワイヤレスアンテナと、ナノコントローラーとナノ粒子ストア間のナノ粒子リンクを備えた操作コードを含む小さなメモリが含まれています。ナノ粒子リポジトリには、いくつかの異なるタイプのナノ粒子が含まれています。ナノゲートの開閉、および開口時間は、送達される粒子の数を調整するために制御されます。
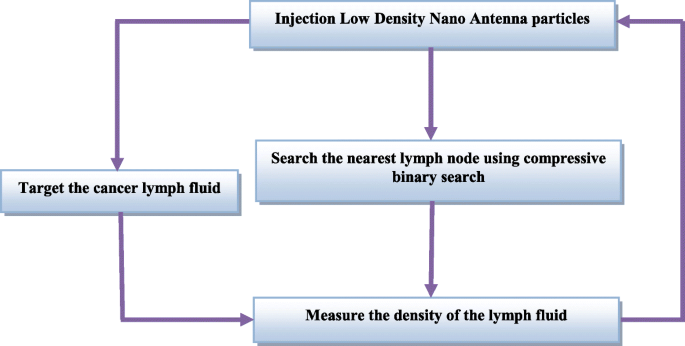
ナノ粒子と戦うプロセスを癌細胞に送る
提案された薬物システムで使用されるナノ粒子の性質の説明
次のセクションでは、提案されたドラッグデリバリーシステムで利用されるナノ粒子の性質について説明します。この作業では、以前のレポート[22]で説明されているように、低密度の嫌気性ナノ粒子が使用されました。
低密度ナノ粒子
腫瘍がリンパ液に囲まれているリンパ液への浸透プロセスとして、癌に対する化合物ナノ粒子のドラッグデリバリープロセスを考えてみてください。黒色腫の組成はリンパ液に似ています。提案された分析モデルは、3つの異なるタイプのナノ粒子からなるナノチューブシステムに基づいています。ナノ粒子は高密度のリンパ液に入れられます。球面極座標で固体Aの特定のナノ粒子を A として定義できます。 =(ra、ϑ a 、φa)、ここで、raは固体Aのナノ粒子の半径座標、ϑ a は固体Aのナノ粒子の天頂座標であり、φaは固体Aのナノ粒子の方位座標です。固体Bの対応する座標は B です。 =(rb、ϑb、φb)であり、ソリッドNの対応する座標は N です。 =(rn、ϑn、φn)、それぞれ。ホジキンリンパ腫のがん細胞の影響を受けるリンパ節には、圧痛と腫れの2つの特性があることを考慮してください。圧痛特性Tpのリンパ節はTp( N 、 t );これは、固体Nのナノ粒子の流体に関連するTpの値が時間とともに変化することを意味します。ここで、入札特性における複合ナノ粒子の総効果は次のように定義されていると考えてみましょう。
$$ \ mathrm {Tpt} =\ mathrm {Tp} \ \ left(A、t \ right)+ \ mathrm {Tp} \ \ left(B、t \ right)+。\ dots \ does \ dots \ dots + \ mathrm {Tp} \ \ left(N、t \ right)$$(1)膨張したプロパティの同じケースを考えてみましょう。これは次のように定義できます。
$$ \ mathrm {Tst} =\ mathrm {Ts} \ \ left(A、t \ right)+ \ mathrm {Ts} \ \ left(B、t \ right)+。\ dots \ does \ dots \ dots + \ mathrm {Ts} \ \ left(N、t \ right)$$(2)式から図1および2では、両方のプロパティの経時変化率は次のように決定できます。
$$ \ frac {\ partial \ left(\ mathrm {Tp} \ left(A、t \ right)\ right)} {\ partial t} + \ frac {\ partial \ left(\ mathrm {Tp} \ left( B、t \ right)\ right)} {\ partial t} + \ dots \ frac {\ partial \ left(\ mathrm {Tp} \ left(N、t \ right)\ right)} {\ partial t} =\ frac {\ mathrm {\ partial Tp}(t)} {\ mathrm {\ partial t}} $$(3)$$ \ frac {\ partial \ left(\ mathrm {Ts} \ left(A、t \ right)\ right)} {\ partial t} + \ frac {\ partial \ left(\ mathrm {Ts} \ left(B、t \ right)\ right)} {\ partial t} + \ dots \ frac {\部分的な\ left(\ mathrm {Ts} \ left(N、t \ right)\ right)} {\ partial t} =\ frac {\ mathrm {\ partial Ts}(t)} {\ partial t} $$( 4)固体Nの1つのナノ粒子が占めることができるリンパ液中の点は次のように定義されます:
$$ {\ mathrm {Po}} _ n =\ mathrm {Po} {\ left(\ mathrm {po}、t \ right)} _ n $$(5)柔らかいリンパ液の固体N誘導体のナノ粒子が\(\ frac {\ partial {\ left(\ mathrm {Tp} \ left(N、t \ right)\ right)} _ {\として定義されていると考えてみましょう。 mathrm {po}}} {\ partial t} \)の場合、柔らかいリンパ液の複合物質微分は次のようになります。
$$ \ frac {\ partial {\ left(\ mathrm {Tp} \ left(A、t \ right)\ right)} _ {\ mathrm {po}}} {\ partial t} + \ frac {\ partial { \ left(\ mathrm {Tp} \ left(B、t \ right)\ right)} _ {\ mathrm {po}}} {\ partial t} + \ dots \ frac {\ partial {\ left(\ mathrm { Tp} \ left(N、t \ right)\ right)} _ {\ mathrm {po}}} {\ partial t} =\ frac {\ mathrm {\ partial Tp} {(t)} _ {\ mathrm { po}}} {\ partial t} $$(6)$$ \ frac {\ partial {\ left(\ mathrm {Ts} \ left(A、t \ right)\ right)} _ {\ mathrm {po} }} {\ partial t} + \ frac {\ partial {\ left(\ mathrm {Ts} \ left(B、t \ right)\ right)} _ {\ mathrm {po}}} {\ partial t} + \ dots \ frac {\ partial {\ left(\ mathrm {Ts} \ left(N、t \ right)\ right)} _ {\ mathrm {po}}} {\ partial t} =\ frac {\ mathrm { \ partial Ts} {(t)} _ {\ mathrm {po}}} {\ partial t} $$(7)固体Nの対応する速度成分は( v rn 、 v ϑn 、 v φn )。次に、固体Nの粒子の流速は、リンパ液の動的粘度dν、および p でナビエ-ストークス方程式を使用して表されます。 は圧力であり、ρ は次のようなリンパ液の密度です:
$$ \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ partial t} + {v} _ {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn }}} {\ mathrm {\ partial rn}} + \ frac {v _ {\ upvartheta \ mathrm {n}}} {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}} } {\ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac { \ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}}-\ frac {v _ {\ upvartheta \ mathrm {n}} ^ 2} {\ mathrm {rn}}- \ frac {v _ {\ upvarphi \ mathrm {n}} ^ 2} {\ mathrm {rn}} + \ frac {1} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rn}}- \ mathrm {d} \ upnu \ left [\ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn}} \ left({\ mathrm {rn} } ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right)+ \ frac {1} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial {v } _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right)+ \ frac {1} {{\ mathrm {rn}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {n}} \ frac {\ partial ^ 2 {v} _ {\ ma thrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2} +-\ frac {2 {v} _ {\ mathrm {rn}}} {{\ mathrm {rn}} ^ 2} -\ frac {2} {{\ mathrm {rn}} ^ 2 \ sin \ upvartheta \ mathrm {n}} \ frac {\ partial \ left({v} _ {\ upvartheta \ mathrm {n}} \ mathrm { sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\ partial \ upvartheta n}}-\ frac {2} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm { n}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}}} \ right] =0 $$(8)リンパ液の動的粘度dνは次のように計算されます。
$$ \ mathrm {d} \ upnu =\ frac {\ left [\ frac {\ partial {v} _ {\ mathrm {rn}}} {\ partial t} + {v} _ {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} + \ frac {v _ {\ upvartheta \ mathrm {n}} \ partial {v} _ {\ mathrm { rn}}} {\ mathrm {rn} \ \ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}}-\ frac {v _ {\ upvartheta \ mathrm {n}} ^ 2 } {\ mathrm {rn}}-\ frac {v _ {\ upvarphi \ mathrm {n}} ^ 2} {\ mathrm {rn}} + \ frac {1 \ \ partial p} {\ uprho \ partial \ mathrm { rn}} \ right]} {\ left [\ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn}} \ left({\ mathrm {rn }} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right)+ \ frac {1} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial { v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right)+ \ frac {1} {{\ mathrm {rn}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {n}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2} +-\ frac {2 {v} _ {\ mathrm {rn}}} {{\ mathrm {rn}} ^ 2}-\ frac {2} {{\ mathrm {rn}} ^ 2 \ sin \ upvartheta \ mathrm {n}} \ frac {\ partial \ left({v} _ {\ upvartheta \ mathrm {n}} \ mathrm {sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\ partial \ upvartheta n}}-\ frac {2} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}}} \ right]} $$( 9)固体AとBのナビエ-ストークス方程式は、次の式で表すことができます。したがって、式8および9。 9は次のように表すことができます:
$$ \ mathrm {d} \ upnu =\ frac {\ left [\ frac {\ partial {v} _ {\ mathrm {rn}}} {\ partial t} + {v} _ {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} + \ frac {v _ {\ upvartheta \ mathrm {n}}} {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}}-\ frac {v _ {\ upvartheta \ mathrm { n}} ^ 2} {\ mathrm {rn}}-\ frac {v _ {\ upvarphi \ mathrm {n}} ^ 2} {\ mathrm {rn}} + \ frac {1} {\ rho} \ frac { \ partial p} {\ mathrm {\ partial rn}} \ right]} {\ left [\ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn }} \ left({\ mathrm {rn}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right)+ \ frac {1} { {\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right)+ \ frac {1} {{\ mathrm { rn}} ^ 2 {\ sin} ^ 2 \ upvartheta \ math rm {n}} \ frac {\ partial ^ 2 {\ mathrm {v}} _ {\ mathrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2}-\ frac {2 {\ mathrm {v}} _ {\ mathrm {rn}}} {{\ mathrm {rn}} ^ 2}-\ frac {2} {{\ mathrm {rn}} ^ 2 \ sin \ upvartheta \ mathrm {n} } \ frac {\ partial \ left({\ mathrm {v}} _ {\ upvartheta \ mathrm {n}} \ mathrm {sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\ partial \ upvartheta n}}-\ frac {2} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {\ mathrm {v}} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}}} \ right]} =\ frac {\ left [\ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial t}} + {\ mathrm {v}} _ {\ mathrm {ra}} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm { \ partial ra}} + \ frac {{\ mathrm {v}} _ {\ upvartheta \ mathrm {a}}} {\ mathrm {ra}} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} + \ frac {{\ mathrm {v}} _ {\ upvarphi \ mathrm {a}}} {\ mathrm {ra} \ \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvarphi a}}-\ frac {{\ mathrm {v} } _ {\ upvartheta \ mathrm {a}} ^ 2} {\ mathrm {ra}}- \ frac {{\ mathrm {v}} _ {\ upvarphi \ mathrm {a}} ^ 2} {\ mathrm {ra}} + \ frac {1} {\ uprho} \ frac {\ mathrm {\ partial p} } {\ mathrm {\ partial ra}} \ right]} {\ left [\ frac {1} {{\ mathrm {ra}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial ra}} \ left({\ mathrm {ra}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial ra}} \ right)+ \ frac {1} {{\ mathrm {ra}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta a}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {a } \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} \ right)+ \ frac {1} {{\ mathrm {ra}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {a}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {ra}}} {\ partial {\ upvarphi \ mathrm {a}} ^ 2}-\ frac { 2 {v} _ {\ mathrm {ra}}} {{\ mathrm {ra}} ^ 2}-\ frac {2} {{\ mathrm {ra}} ^ 2 \ sin \ upvartheta \ mathrm {a}} \ frac {\ partial \ left({v} _ {\ upvartheta \ mathrm {a}} \ mathrm {sin} \ upvartheta \ mathrm {a} \ right)} {\ mathrm {\ partial \ upvartheta a}}-\ frac {2} {{\ mathrm {ra}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {a}}} {\ partial_ { \ upvarphi \ mathrm {a}}} \ right]} =\ frac { \ left [\ frac {\ partial {v} _ {\ mathrm {rb}}} {\ partial t} + {v} _ {\ mathrm {rb}} \ frac {\ partial {v} _ {\ mathrm { rb}}} {\ mathrm {\ partial rb}} + \ frac {v _ {\ upvartheta \ mathrm {b}}} {\ mathrm {rb}} \ frac {\ partial {v} _ {\ mathrm {rb} }} {\ mathrm {\ partial \ upvartheta b}} + \ frac {v _ {\ upvarphi \ mathrm {b}}} {\ mathrm {rb} \ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvarphi b}}-\ frac {v _ {\ upvartheta \ mathrm {b}} ^ 2} {\ mathrm {rb}} -\ frac {v _ {\ upvarphi \ mathrm {b}} ^ 2} {\ mathrm {rb}} + \ frac {1} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rb}} \ right]} {\ left [\ frac {1} {{\ mathrm {rb}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rb}} \ left({\ mathrm {rb}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial rb}} \ right)+ \ frac {1} {{\ mathrm {rb}} ^ 2 \ mathrm {sin } \ upvartheta \ mathrm {b}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta b}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {b} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} \ right)+ \ frac {1} {{\ mathrm {rb}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {b }} \ frac {\ partial ^ 2 {v} _ {\ mathrm { rb}}} {\ partial {\ upvarphi \ mathrm {b}} ^ 2}-\ frac {2 {v} _ {\ mathrm {rb}}} {{\ mathrm {rb}} ^ 2}-\ frac {2} {{\ mathrm {rb}} ^ 2 \ sin \ upvartheta \ mathrm {b}} \ frac {\ partial \ left({v} _ {\ upvartheta \ mathrm {b}} \ mathrm {sin} \ upvartheta \ mathrm {b} \ right)} {\ mathrm {\ partial \ upvartheta b}}-\ frac {2} {{\ mathrm {rb}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {b}}} {\ partial _ {\ upvarphi \ mathrm {b}}} \ right]} $$(10)粒子はナノ次元です。したがって、それらの半径は非常に小さくなり、簡単にするために、式(1)は次のようになります。 10は次のように表されます:
$$ \ mathrm {d} \ upnu =\ left [\ frac {v _ {\ upvartheta \ mathrm {n}}} {\ mathrm {rn}} \ frac {\ partial {v} _ {\ mathrm {rn}} } {\ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac { \ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}}-\ frac {v _ {\ upvartheta \ mathrm {n}} ^ 2} {\ mathrm {rn}}- \ frac {v _ {\ upvarphi \ mathrm {n}} ^ 2} {\ mathrm {rn}} + \ frac {1} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rn}} \右] / \ left [\ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn}} \ left({\ mathrm {rn}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right)+ \ frac {1} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial {\ mathrm {v} } _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right)+ \ frac {1} {{\ mathrm {rn}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {n}} \ frac {\ partial ^ 2 {\ mathrm {v}} _ {\ mathrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2}-\ frac {2 {\ mathrm {v}} _ {\ mathrm {rn}}} {{\ math rm {rn}} ^ 2}-\ frac {2} {{\ mathrm {rn}} ^ 2 \ sin \ upvartheta \ mathrm {n}} \ frac {\ partial \ left({\ mathrm {v}} _ {\ upvartheta \ mathrm {n}} \ mathrm {sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\ partial \ upvartheta n}}-\ frac {2} {{\ mathrm {rn}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {\ mathrm {v}} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}} } \ right] =\ left [\ frac {{\ mathrm {v}} _ {\ upvartheta \ mathrm {a}}} {\ mathrm {ra}} \ frac {\ partial {\ mathrm {v}} _ { \ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} + \ frac {{\ mathrm {v}} _ {\ upvarphi \ mathrm {a}}} {\ mathrm {ra} \ \ mathrm { sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvarphi a}}-\ frac {{\ mathrm { v}} _ {\ upvartheta \ mathrm {a}} ^ 2} {\ mathrm {ra}}-\ frac {{\ mathrm {v}} _ {\ upvarphi \ mathrm {a}} ^ 2} {\ mathrm {ra}} + \ frac {1} {\ uprho} \ frac {\ mathrm {\ partial p}} {\ mathrm {\ partial ra}} \ right] / \ left [\ frac {1} {{\ mathrm {ra}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial ra}} \ left({\ mathrm {ra}} ^ 2 \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial ra}} \ rig ht)+ \ frac {1} {{\ mathrm {ra}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta a}} \ left (\ mathrm {sin} \ upvartheta \ mathrm {a} \ frac {\ partial {\ mathrm {v}} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} \ right)+ \ frac {1} {{\ mathrm {ra}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {a}} \ frac {\ partial ^ 2 {\ mathrm {v}} _ {\ mathrm {ra}} } {\ partial {\ upvarphi \ mathrm {a}} ^ 2}-\ frac {2 {\ mathrm {v}} _ {\ mathrm {ra}}} {{\ mathrm {ra}} ^ 2}-\ frac {2} {{\ mathrm {ra}} ^ 2 \ sin \ upvartheta \ mathrm {a}} \ frac {\ partial \ left({\ mathrm {v}} _ {\ upvartheta \ mathrm {a}} \ mathrm {sin} \ upvartheta \ mathrm {a} \ right)} {\ mathrm {\ partial \ upvartheta a}}-\ frac {2} {{\ mathrm {ra}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {a}}} {\ partial _ {\ upvarphi \ mathrm {a}}} \ right] =\ left [\ frac {v _ {\ upvartheta \ mathrm {b}}} {\ mathrm {rb}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} + \ frac {v _ {\ upvarphi \ mathrm {b}}} {\ mathrm {rb} \ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\部分的 \ upvarphi b}}-\ frac {v _ {\ upvartheta \ mathrm {b}} ^ 2} {\ mathrm {rb}}-\ frac {v _ {\ upvarphi \ mathrm {b}} ^ 2} {\ mathrm {rb }} + \ frac {1} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rb}} \ right] / \ left [\ frac {1} {{\ mathrm {rb}} ^ 2 } \ frac {\ partial} {\ mathrm {\ partial rb}} \ left({\ mathrm {rb}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\部分的なrb}} \ right)+ \ frac {1} {{\ mathrm {rb}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta b}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {b} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} \ right)+ \ frac {1} {{\ mathrm {rb}} ^ 2 {\ sin} ^ 2 \ upvartheta \ mathrm {b}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {rb}}} {\部分的な{\ upvarphi \ mathrm {b}} ^ 2}-\ frac {2 {v} _ {\ mathrm {rb}}} {{\ mathrm {rb}} ^ 2}-\ frac {2} {{\ mathrm {rb}} ^ 2 \ sin \ upvartheta \ mathrm {b}} \ frac {\ partial \ left({v} _ {\ upvartheta \ mathrm {b}} \ mathrm {sin} \ upvartheta \ mathrm {b} \ right)} {\ mathrm {\ partial \ upvartheta b}}-\ frac {2} {{\ mathrm {rb}} ^ 2 \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial { v} _ {\ upvarphi \ mathrm {b}}} {\ partial _ {\ upvarphi \ mathrm {b}}} \ right] $$(11)式11は次のように表すことができます。
$$ \ mathrm {d} \ upnu =\ mathrm {rn} \ left [{v} _ {\ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} + \ frac {v _ {\ upvarphi \ mathrm {n}}} {\ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvarphi n}}-{v} _ {\ upvartheta \ mathrm {n}} ^ 2- {v} _ {\ upvarphi \ mathrm {n}} ^ 2 + \ frac {\ mathrm {rn}} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rn}} \ right] / \ left [\ frac {\ partial} {\ mathrm {\ partial rn} } \ left({\ mathrm {rn}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rn}}} {\ mathrm {\ partial rn}} \ right)+ \ frac {1} {\ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta n}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {n} \ frac {\ partial { v} _ {\ mathrm {rn}}} {\ mathrm {\ partial \ upvartheta n}} \ right)+ \ frac {1} {\ sin ^ 2 \ upvartheta \ mathrm {n}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {rn}}} {\ partial {\ upvarphi \ mathrm {n}} ^ 2} -2 {v} _ {\ mathrm {rn}}-\ frac {2} {\ sin \ upvartheta \ mathrm {n}} \ frac {\ partial \ left({v} _ {\ upvartheta \ mathrm {n}} \ mathrm {sin} \ upvartheta \ mathrm {n} \ right)} {\ mathrm {\パーtial \ upvartheta n}}-\ frac {2} {\ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {n}}} {\ partial _ {\ upvarphi \ mathrm {n}}} \ right] =\ mathrm {ra} \ left [{v} _ {\ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvartheta a}} + \ frac {v _ {\ upvarphi \ mathrm {a}}} {\ \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial \ upvarphi a}}-{v} _ {\ upvartheta \ mathrm {a}} ^ 2- {v} _ {\ upvarphi \ mathrm {a}} ^ 2 + \ frac {\ mathrm {ra}} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial ra}} \ right] / \ left [\ frac {\ partial} {\ mathrm {\ partial ra}} \ left({\ mathrm {ra}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {ra}}} {\ mathrm {\ partial ra}} \ right)+ \ frac {1} {\ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta a}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {a} \ frac {\部分的な{v} _ {\ mathrm {ra}}} {\ mathrm {\部分的な\ upvartheta a}} \ right)+ \ frac {1} {\ sin ^ 2 \ upvartheta \ mathrm {a}} \ frac {\部分的^ 2 {v} _ {\ mathrm {ra}}} {\ partial {\ upvarphi \ mathrm {a}} ^ 2} -2 {v} _ {\ mathrm {ra}}-\ frac {2} { \罪\ upvartheta \ mathrm {a}} \ frac {\ partial \ left({v} _ {\ upvartheta \ mathrm {a}} \ mathrm {sin} \ upvartheta \ mathrm {a} \ right)} {\ mathrm {\部分的な\ upvartheta a}}-\ frac {2} {\ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {a}}} {\ partial _ {\ upvarphi \ mathrm {a}}} \ right] =\ mathrm {rb} \ left [{v} _ {\ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvartheta b}} + \ frac {v _ {\ upvarphi \ mathrm {b}}} {\ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial \ upvarphi b}}-{v} _ {\ upvartheta \ mathrm {b}} ^ 2- {v} _ {\ upvarphi \ mathrm {b}} ^ 2 + \ frac {\ mathrm {rb}} {\ rho} \ frac {\ partial p} {\ mathrm {\ partial rb}} \ right] / \ left [\ frac {\ partial} {\ mathrm {\ partial rb}} \ left({\ mathrm {rb}} ^ 2 \ frac {\ partial {v} _ {\ mathrm {rb}}} {\ mathrm {\ partial rb}} \ right)+ \ frac {1} {\ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta b}} \ left(\ mathrm {sin} \ upvartheta \ mathrm {b} \ frac {\部分的な{v} _ {\ mathrm {rb}}} {\ mathrm {\部分的な\ upvartheta b}} \ right)+ \ frac {1} {\ si n ^ 2 \ upvartheta \ mathrm {b}} \ frac {\ partial ^ 2 {v} _ {\ mathrm {rb}}} {\ partial {\ upvarphi \ mathrm {b}} ^ 2} -2 {v} _ {\ mathrm {rb}}-\ frac {2} {\ sin \ upvartheta \ mathrm {b}} \ frac {\ partial \ left({v} _ {\ upvartheta \ mathrm {b}} \ mathrm {sin } \ upvartheta \ mathrm {b} \ right)} {\ mathrm {\ partial \ upvartheta b}}-\ frac {2} {\ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v } _ {\ upvarphi \ mathrm {b}}} {\ partial _ {\ upvarphi \ mathrm {b}}} \ right] $$(12)ナノ粒子の半径と癌によるリンパの粘度の間には直接的な関係があります。リンパ液が静的で粘性が高くなりすぎると、その機能を適切に実行できなくなります。これは、毒素を循環させて浄化し、癌と戦うのに役立ちます。ナノ粒子のサイズが小さければ、リンパ腫細胞は簡単に殺されます。化合物ナノ粒子の総量の輸送を説明するために、連続の方程式を使用して、固体A、B、およびNの3つのナノ粒子を次のように仮定します。
$$ \ frac {1} {{\ mathrm {ra}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial ra}} \ left({\ mathrm {ra}} ^ 2 {v} _ { \ mathrm {ra}} \ right)+ \ frac {1} {\ mathrm {ra} \ \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta a }} \ left(\ sin {\ upvartheta \ mathrm {v}} _ {\ upvartheta \ mathrm {a}} \ right)+ \ frac {1} {\ mathrm {ra} \ \ mathrm {sin} \ upvartheta \ mathrm {a}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm {a}}} {\ mathrm {\ partial \ upvarphi a}} + \ frac {1} {{\ mathrm {rb}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rb}} \ left({\ mathrm {rb}} ^ 2 {v} _ {\ mathrm {rb}} \ right)+ \ frac {1} { \ mathrm {rb} \ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial} {\ mathrm {\ partial \ upvartheta b}} \ left(\ sin {\ upvartheta v} _ {\ upvartheta \ mathrm {b}} \ right)+ \ frac {1} {\ mathrm {rb} \ \ mathrm {sin} \ upvartheta \ mathrm {b}} \ frac {\ partial {v} _ {\ upvarphi \ mathrm { b}}} {\ mathrm {\ partial \ upvarphi b}} + \ frac {1} {{\ mathrm {rn}} ^ 2} \ frac {\ partial} {\ mathrm {\ partial rn}} \ left( {\ mathrm {rn}} ^ 2 {v} _ {\ mathrm {rn}} \ right)+ \ frac {1} {\ mathrm {rn} \ \ mathrm {sin} \ upvartheta \ mathrm {n}} \ frac {\ parti al} {\ mathrm {\ partial \ upvartheta n}} \ left(\ sin {\ upvartheta v} _ {\ upvartheta \ mathrm {n}} \ right)+ \ frac {1} {\ mathrm {rn} \ \ mathrm{sin}\upvartheta \mathrm{n}}\frac{\partial {v}_{\upvarphi \mathrm{n}}}{\mathrm{\partial \upvarphi n}}=0 $$ (13)The dynamic fluid viscosity could be determined from the following equation [23]:
$$ \mathrm{Vs}=\frac{2}{9}\frac{r^2g\ \left(\uprho \mathrm{p}-\uprho \mathrm{f}\right)}{\mathrm{dv}} $$ (14)where Vs is the particles’ settling velocity (m/s), r is the Stokes radius of the particle (m), g is the gravitational acceleration (m/s 2 ), ρp is the density of the particles (kg/m 3 ), ρf is the density of the fluid (kg/m 3 ), and dv is the (dynamic) fluid viscosity (Pa·s). The lymph fluid is slightly heavier than water (lymph density = 1019 kg/m 3 , water density = 998.28 kg/m 3 at 20 °C). As a reference value, we consider the dynamic viscosity of the water to be 1.002 × 10 –3 kg m –1 s –1 。
Dynamic viscosity is the measurement of the fluid’s internal resistance to flow, while kinematic viscosity refers to the ratio of dynamic viscosity to density. The effect of all the nanoparticles on the fluid viscosity is represented as follows:
$$ \mathrm{dv}=\frac{2\mathrm{g}}{9}\left[\frac{{\mathrm{ra}}^2\left(\uprho \mathrm{a}-\uprho \mathrm{f}\right)}{\mathrm{vsa}}+\frac{{\mathrm{rb}}^2\left(\uprho \mathrm{b}-\uprho \mathrm{f}\right)}{\mathrm{vsb}}+\frac{{\mathrm{rn}}^2\left(\uprho \mathrm{n}-\uprho \mathrm{f}\right)}{\mathrm{vn}}\right] $$ (15)By comparing Eq. 12 and Eq. 15, the following equation could be emerged:
$$ \left|\frac{2\mathrm{g}}{9}\left[\frac{{\mathrm{ra}}^2\left(\uprho \mathrm{a}-\uprho \mathrm{f}\right)}{\mathrm{vsa}}+\frac{{\mathrm{rb}}^2\left(\uprho \mathrm{b}-\uprho \mathrm{f}\right)}{\mathrm{vsb}}+\frac{{\mathrm{rn}}^2\left(\uprho \mathrm{n}-\uprho \mathrm{f}\right)}{\mathrm{vn}}\right]\right|=\mathrm{rn}\left[{v}_{\upvartheta \mathrm{n}}\frac{\partial {v}_{\mathrm{rn}}}{\mathrm{\partial \upvartheta n}}+\frac{v_{\upvarphi \mathrm{n}}}{\ \mathrm{sin}\upvartheta \mathrm{n}}\frac{\partial {v}_{\mathrm{rn}}}{\mathrm{\partial \upvarphi n}}-{v}_{\upvartheta \mathrm{n}}^2-{v}_{\upvarphi \mathrm{n}}^2+\frac{\mathrm{rn}}{\uprho \mathrm{f}}\frac{\mathrm{\partial p}}{\mathrm{\partial rn}}\right]/\left[\frac{\partial }{\mathrm{\partial rn}}\left({\mathrm{rn}}^2\frac{\partial {v}_{\mathrm{rn}}}{\mathrm{\partial rn}}\right)+\frac{1}{\mathrm{sin}\upvartheta \mathrm{n}}\frac{\partial }{\mathrm{\partial \upvartheta n}}\left(\mathrm{sin}\upvartheta \mathrm{n}\frac{\partial {v}_{\mathrm{rn}}}{\mathrm{\partial \upvartheta n}}\right)+\frac{1}{\sin^2\upvartheta \mathrm{n}}\frac{\partial^2{v}_{\mathrm{rn}}}{\partial {\upvarphi \mathrm{n}}^2}-2{v}_{\mathrm{rn}}-\frac{2}{\sin \upvartheta \mathrm{n}}\frac{\partial \left({v}_{\upvartheta \mathrm{n}}\mathrm{sin}\upvartheta \mathrm{n}\right)}{\mathrm{\partial \upvartheta n}}-\frac{2}{\mathrm{sin}\upvartheta \mathrm{n}}\frac{\partial {v}_{\upvarphi \mathrm{n}}}{\partial_{\upvarphi \mathrm{n}}}\right]=\mathrm{ra}\left[{v}_{\upvartheta \mathrm{a}}\frac{\partial {v}_{\mathrm{ra}}}{\mathrm{\partial \upvartheta a}}+\frac{v_{\upvarphi \mathrm{a}}}{\ \mathrm{sin}\upvartheta \mathrm{a}}\frac{\partial {v}_{\mathrm{ra}}}{\mathrm{\partial \upvarphi a}}-{v}_{\upvartheta \mathrm{a}}^2-{v}_{\upvarphi \mathrm{a}}^2+\frac{\mathrm{ra}}{\uprho \mathrm{f}}\frac{\partial p}{\mathrm{\partial ra}}\right]/\left[\frac{\partial }{\mathrm{\partial ra}}\left({\mathrm{ra}}^2\frac{\partial {v}_{\mathrm{ra}}}{\mathrm{\partial ra}}\right)+\frac{1}{\mathrm{sin}\upvartheta \mathrm{a}}\frac{\partial }{\mathrm{\partial \upvartheta a}}\left(\mathrm{sin}\upvartheta \mathrm{a}\frac{\partial {v}_{\mathrm{ra}}}{\mathrm{\partial \upvartheta a}}\right)+\frac{1}{\sin^2\upvartheta \mathrm{a}}\frac{\partial^2{v}_{\mathrm{ra}}}{\partial {\upvarphi \mathrm{a}}^2}-2{v}_{\mathrm{ra}}-\frac{2}{\sin \upvartheta \mathrm{a}}\frac{\partial \left({v}_{\upvartheta \mathrm{a}}\mathrm{sin}\upvartheta \mathrm{a}\right)}{\mathrm{\partial \upvartheta a}}-\frac{2}{\mathrm{sin}\upvartheta \mathrm{a}}\frac{\partial {v}_{\upvarphi \mathrm{a}}}{\partial_{\upvarphi \mathrm{a}}}\right]=\mathrm{rb}\left[{v}_{\upvartheta \mathrm{b}}\frac{\partial {v}_{\mathrm{rb}}}{\mathrm{\partial \upvartheta b}}+\frac{v_{\upvarphi \mathrm{b}}}{\ \mathrm{sin}\upvartheta \mathrm{b}}\frac{\partial {v}_{\mathrm{rb}}}{\mathrm{\partial \upvarphi b}}-{v}_{\upvartheta \mathrm{b}}^2-{v}_{\upvarphi \mathrm{b}}^2+\frac{\mathrm{rb}}{\uprho \mathrm{f}}\frac{\partial p}{\mathrm{\partial rb}}\right]/\left[\frac{\partial }{\mathrm{\partial rb}}\left({\mathrm{rb}}^2\frac{\partial {v}_{\mathrm{rb}}}{\mathrm{\partial rb}}\right)+\frac{1}{\mathrm{sin}\upvartheta \mathrm{b}}\frac{\partial }{\mathrm{\partial \upvartheta b}}\left(\mathrm{sin}\upvartheta \mathrm{b}\frac{\partial {v}_{\mathrm{rb}}}{\mathrm{\partial \upvartheta b}}\right)+\frac{1}{\sin^2\upvartheta \mathrm{b}}\frac{\partial^2{v}_{\mathrm{rb}}}{\partial {\upvarphi \mathrm{b}}^2}-2{v}_{\mathrm{rb}}-\frac{2}{\sin \upvartheta \mathrm{b}}\frac{\partial \left({v}_{\upvartheta \mathrm{b}}\mathrm{sin}\upvartheta \mathrm{b}\right)}{\mathrm{\partial \upvartheta b}}-\frac{2}{\mathrm{sin}\upvartheta \mathrm{b}}\frac{\partial {v}_{\upvarphi \mathrm{b}}}{\partial_{\upvarphi \mathrm{b}}}\right] $$ (16)Equation 16 depicts the relationship between the density of the lymph fluid, the density of the nanoparticles of the compound drug system, and the radius of the nanoparticles. There is a positive correlation between the density of the lymph fluid and the density of the nanoparticles. The smaller the density and radius of nanoparticles, the lesser the density of the fluid will be. As established earlier, the decrease in the density of the lymph fluid leads to its inability to reproduce and reduce the ferocity of the disease. It can, therefore, be concluded that the tumor can be cured by minimizing the size of nanoparticles. These particles can reach in the range of up to 0.1 nm (i.e., Angstrom or picometer range). The particles of this size can act as the nucleus of drug delivery in this drug system. Equation 16 shows that radii of the nanoparticles in the proposed drug system are related to the effectiveness of the delivery system. Much lower sized nanoparticles can reduce the density of lymph fluid and the spread of the disease.
Nanoparticles with Nanoantennas
This study used the nanoparticle described in an earlier report [22] as an emissary with a nano-microcontroller. In the system, the proposed transmission distance is very small and compatible with the composition of nanoparticles. Thus, the middle gap can be neglected in mid-distance and is symbolized by C d 。 Further, R a および X a are the real part and the imaginary part of the anaerobic impedance. After neglecting the load of the intercellular space between the nanoparticles and the nano-microcontroller, R a および X a can be calculated as follows [22]:
$$ {R}_a=\frac{r_{a0}}{1+{C}_d{w}_a\left(2{x}_{a0}+{C}_d\left({r_{a0}}^2+{x_{a0}}^2\right){w}_a\right)} $$ (17) $$ {X}_a=\frac{x_0-{C}_d\left({r_{a0}}^2+{x_{a0}}^2\right){w}_a}{1+{C}_d{w}_a\left(2{x}_{a0}+{C}_d\left({r_{a0}}^2+{x_{a0}}^2\right){w}_a\right)} $$ (18)Thus, the load resistance value of nanotubes can be predicted as in the following equation:
$$ {r}_l=\frac{g^2R}{g^2-2 gSX{\varepsilon}_L\omega +{S}^2\left({R}^2+{X}^2\right){\varepsilon_L}^2{\omega}^2} $$ (19)ここで、ε L is the permittivity of the loading material, g is the size of the gap, and S is the effective cross-section area of the gap. In order to simplify the equation, the value of g 2 can be neglected as it is too low and the final equation can be rewritten as follows:
$$ {r}_l=\frac{g^2R}{-2 gSX{\varepsilon}_L\omega +{S}^2\left({R}^2+{X}^2\right){\varepsilon_L}^2{\omega}^2} $$ (20)Then,
$$ {r}_l=\frac{g^2R}{S{\varepsilon}_L\omega \left(-2 gX+S\left({R}^2+{X}^2\right){\varepsilon}_L\omega \right)} $$ (21)The optical nano-photo concept can be used as an effective tool for interpreting and predicting these effects to design and improve nanoscale parameters and increase the nano-sensitivity to serve better as a single molecular sensor. Nanoantenna may provide optimal performance in terms of sensitivity, efficiency, and bandwidth in the process. The next section presents the concept of searching the cancerous lymph nodes using compressive binary search algorithm.
Searching for the Target Lymphatic Nodes Using Compressive Binary Search
In order for nanoparticles to reach the cancerous cells in a fast and efficient manner, we applied compressive binary search by the nano-microcontroller. The guided nanoparticles follow a specific path to quickly reach the target. This movement is based on the information obtained from the “exploratory nanoparticles.” Assume that the target lymph node, Tf, has exactly one nonzero entry, where the location of the lymph node is unknown. The algorithm divides mt measurements into a total of St stages, where St refers to the stages of the lymph nodes. The measurements are more than one for all the stages of the lymph nodes, which is necessary for the algorithm to be executed until completion. Based on this measurement, the algorithm decides between going left or right, until the nanoparticles reach the target, the cancerous lymph node.

結果と考察
In order to analyze the proposed design, the nanoparticles were applied to the following five types of materials:silicone, lithium, lung, helium, and hydrogen. The materials were chosen because of their low density. The lung nanoparticles were samples from nano-sized lung nodules. They appear encircling with white shadows in a chest X-ray or computerized tomography scan taken from the lung of the person and required to be undamaged. The proposed idea is based on the analytical model, which indicates that the smaller the density of nanoparticles, the smaller the dynamic viscosity will be. This will result in a decrease in fluid viscosity. It is shown that the types of materials and the density of each particle will affect settling velocity of nanoparticles at entry into the lymphatic fluid and the density of the lymphatic fluid. We considered the following parameters:acceleration of gravity (g ) = 9.80665, particle diameter (d ) = 10 A, initial density of lymph fluid (ρf) = 998.28, and dynamic viscosity = 0.0010 kg m –1 s –1 [24]. These parameters were selected by the assumption that the viscosity of the lymphatic fluid is very similar to the viscosity of the water and the very small difference does not affect the results of the model. Figure 4 illustrates the density of nanoparticles for five selected materials for application in the proposed analytical model. Figure 5 shows the settling velocity for each particle. Figure 6 shows the effect of the settling velocity of nanoparticles on altering the lymphocyte density of cancer cells. The results shown in Fig. 6 show that the settling velocity of the particles carries a negative value. This indicates that the nanoparticle after entering in the lymphatic fluid rapidly moves in the opposite direction toward their entry into the lymphatic fluid. In general, any object that moves in the negative direction has a negative velocity. This movement of the particle leads to reduced viscosity of the lymphatic fluid.
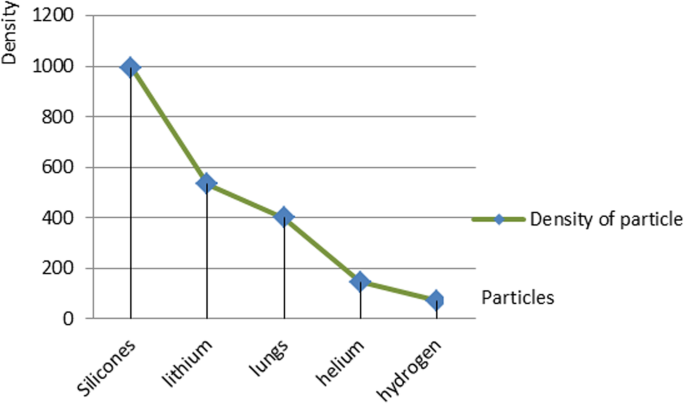
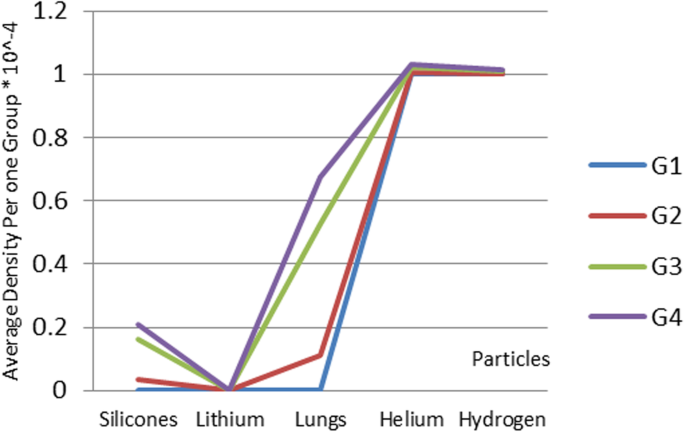
Density of nanoparticles for the five selected materials
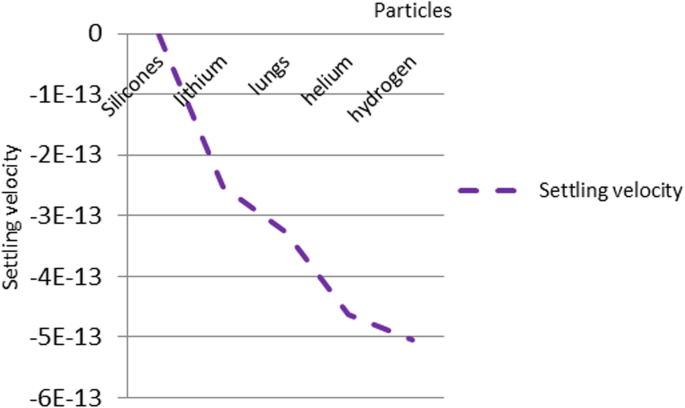
The settling velocity data for each particle
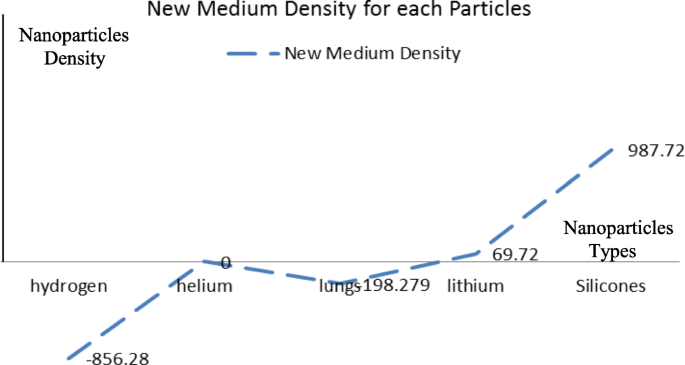
The effect of the settling velocity of nanoparticles on changing the lymphocyte density of cancer cells
Silicone nanoparticles showed the settling velocity of approximately − 2.87 × 10–15 m/s. This resulted in a decrease in viscosity of the lymphatic fluid to 987.72 kg/m 3 for the initial density 998.28 kg/m 3 。 The density is continuously reduced to a point where hydrogen produces extremely spectacular results, i.e., the complete collapse of lymphatic fluid resistance. The density of the lymphatic fluid − 856.28 kg/m 3 with the negative sign indicated that there was no resistance from the lymphatic fluid to the flow of the nanoparticles, resulting in the complete collapse of the liquid fluid. Both the hydrogen and helium particles have a significant impact on the liquid viscosity due to the low density of the particles. Hence, it is important to use a drug system consisting of a group of nanoparticles for low-density materials. Figure 7 shows the relationship between the diameters of lung nanoparticles and the number of nanoparticles in one group. The figure shows that the higher the diameter of nanoparticles, the fewer their number in a group. This is clearly shown at the highest value of the nanoparticle diameter of 1000 nm, where the number of molecules in a group is 20 molecules. Figure 8 shows the relationship between the diameters of lithium nanoparticles and the number of nanoparticles in one group. This figure demonstrates the inverse relationship between the radius of nanoparticles and the number of molecules in a group where lithium particle diameters are significantly lower than the lung nanoparticles, where the number of nanoparticles in Fig. 7 is relatively low compared to the lithium particles as shown in Fig. 8. And the multicolor balls in both figures refer to different ranges of nanoparticle radii for each group, where each group contains a number of nanoparticles with different sizes. The best results can be obtained when hydrogen and helium particles are increased from other substances. A mixture of different materials should be used so that the properties of these substances can be used in the treatment process as well as to reduce viscosity. Figure 9 illustrates the different sets of materials proposed to have the mean highest density of both hydrogen and helium materials. Figure 10 shows the average mass of a nanoparticle in a group. It can be seen that the mass of both hydrogen and helium is the highest compared to the mass of particles of other substances. Figure 11 illustrates the relationship between the diameters of the nanoparticles and the width of its group or class. It is important to note that these results will open up a new area to reduce the resistance of the lymphatic fluid in tumors. This can be achieved using hydrogen nanoparticles of a size in the range of Angstrom. In addition to hydrogen nanoparticles, there may also exist a number of other substances in the same size. Figure 12 illustrates the standard deviation of a number of coefficients for both lung and lithium nanoparticles. These coefficients are limited to fractions of nanoparticles in a single group as well as their number in addition to the diameters of these nanoparticles. It is clear that the group fractions have the less value of the standard deviation. Hence, most of the fractions in the computational processes are around the mean of these values. Figure 13 shows the standard deviation of the mass for particles of silicones, lithium, lungs, helium, and hydrogen in one group. It is clear that the particles of the lung have the largest standard deviation and the lithium has the minimum value.
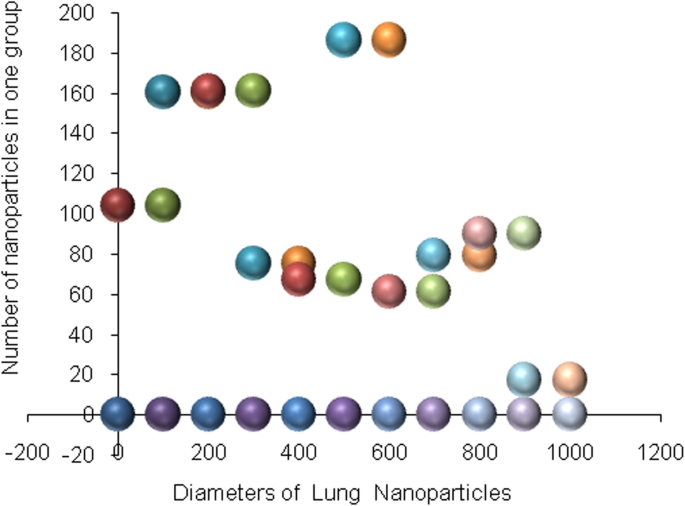
Group of nanoparticles in the lung cells and their number in one of the proposed groups
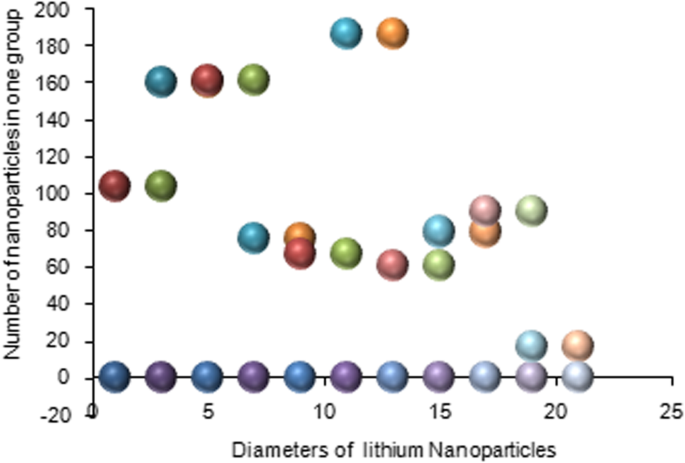
Group of nanoparticles in the lithium cells and their number in one of the proposed groups
Different sets of materials proposed to have the mean highest density of both hydrogen and helium materials
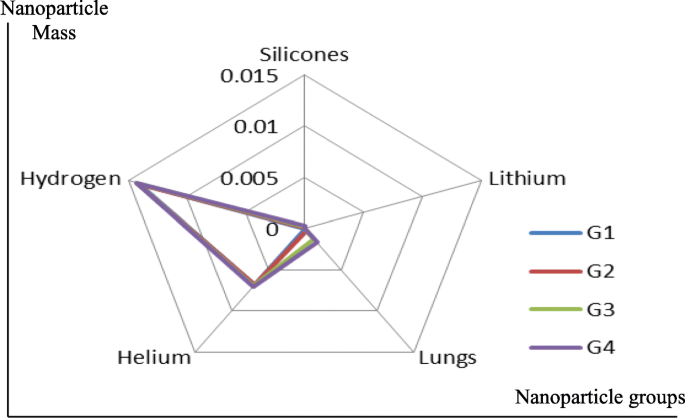
Average mass of a nanoparticle in a group
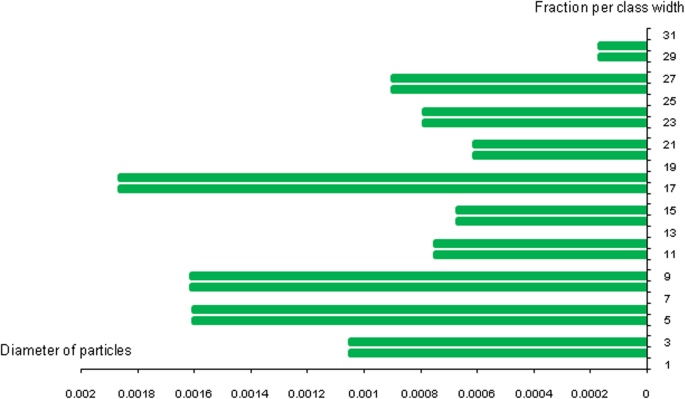
Diameters of the nanoparticles related to the group width
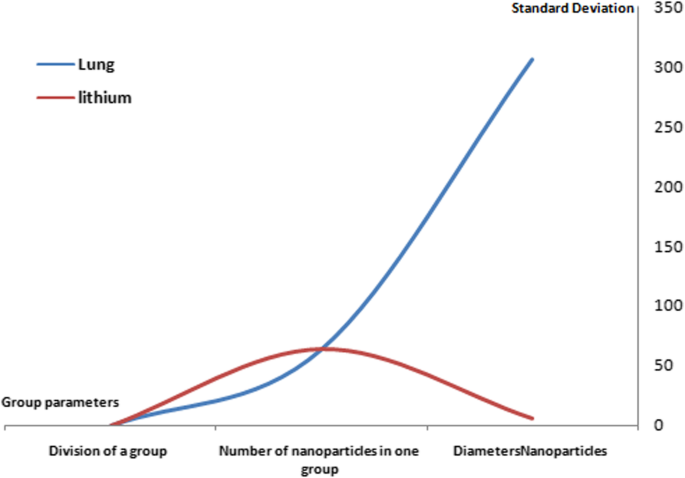
The standard deviation of lung and lithium nanoparticles coefficients
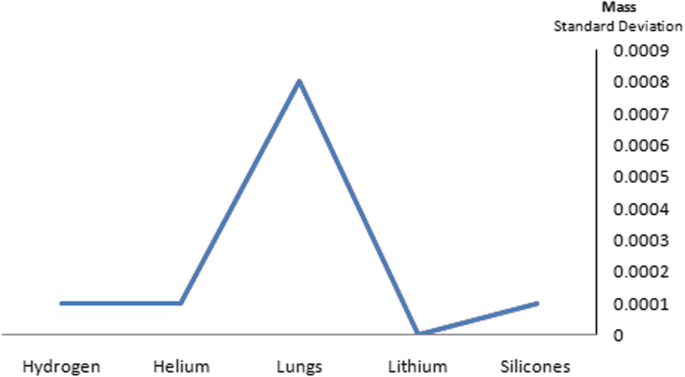
The standard deviation of the mass for particles of silicones, lithium, lungs, helium, and hydrogen in one group
Methods
The aim of this study was to establish a nano-drug delivery system capable of delivering the drugs effectively to the cancer cells. The following methodology was used to deliver nanoparticles:
- i)
Low-density nanoparticles
This study proposed the theoretical approach of nanoparticles as a low-density drug. This depends on the density and the settling velocity of the nanoparticles, as these nanoparticles can overcome the resistance of the lymphatic fluid.
- ii)
Preparation of anaerobic nanoparticles
This study uses the idea of nanoparticles possessing an antenna through which a connection can be made between nanoparticles and nano-controller. The transmission distance was assumed to be too small to match the composition of nanoparticles and also to fit the actual distance between them.
- iii)
Nano-controller design
Its function is to deliver the nanoparticle drug to cancer cells. Its role is to send signals to the nanoparticles and coordinate their actions and direct them to the lymphatic fluid of tumors.
- iv)
Searching for the target lymphatic nodes
The lymphatic nodes are searched using compressive binary search algorithm. This algorithm is characterized by high-speed search, which makes nanoparticles more accessible to infected cells than the conventional methods. The primary supervisor behind the performance of the nanoparticles is the nano-controller. It directs nanoparticles to the infected cells by following this algorithm to ensure that an appropriate number of molecules are in proportional density to the lymphatic fluid.
Conclusion
There have been various studies managing the treatment of malignant growth utilizing nanoparticles. The lymphatic liquid in tumors plays a substantial role in the obstruction of medication to the cancer cells. We developed an intelligent drug delivery system containing a consortium of nanoparticles. The proposed design demonstrates that small nanoparticles result in low density of the fluid. The results indicated that hydrogen particles are most efficient in reducing resistance toward lymphatic liquid owing to their smaller size. Furthermore, the design involves an anaerobic nano-controller that can determine the state and area of the particles. This technique conveys the medication to the infected cell more effectively.
データと資料の可用性
The datasets supporting the results of this article are included within the article.
略語
- LN:
-
Lipid nanoparticles
- NLC:
-
Nanostructured lipid carriers
- PN:
-
Polymeric nanoparticles
- SLNs:
-
固体脂質ナノ粒子
ナノマテリアル
- フェイルセーフ設計
- ドラッグデリバリーを強化するためのナノファイバーとフィラメント
- 生体適合性FePO4ナノ粒子:ドラッグデリバリー、RNA安定化、および機能的活性
- 腫瘍治療のためのドラッグデリバリーシステムとしての環境応答性金属有機フレームワーク
- 癌用途のための細胞ベースのドラッグデリバリー
- ゼブラフィッシュ:ナノテクノロジーを介した神経特異的ドラッグデリバリーのための有望なリアルタイムモデルシステム
- 黒色腫の標的化学療法治療のための薬物送達担体としての131I追跡PLGA-脂質ナノ粒子
- 新規ナノ粒子増強ワーム状ミセルシステムの研究
- ナノテクノロジー:invivoイメージングシステムから制御されたドラッグデリバリーまで
- 多機能GaN / Feナノ粒子による内皮細胞の標的化
- 細胞内タンパク質送達のためのシリカナノ粒子:緑色蛍光タンパク質を使用した新しい合成アプローチ



