リチウムイオン電池のナノ粒子電極における高速変形の化学ポテンシャルの開発された表現

はじめに

携帯型電子機器、電気自動車、大規模エネルギー貯蔵の開発では、リチウム電池に適用するために、リチウムなどのリチウムなどの大容量電極材料を使用することが提案されています[1,2 、3]。均一な体積変形によって引き起こされる応力は拡散によって引き起こされる応力と呼ばれ、周期的な充電と放電の間に脆性破壊を引き起こす可能性があり、この悪影響はバッテリーの容量をさらに低下させます[4]。リチウムイオン電池電極の複合材料は一般に複雑であり、その形態が異なるため、理論や方程式で電池の挙動を説明することはより困難です。理論モデルでは、複合材料の特性は通常、空間座標での電極材料パラメータの変化を考慮してシミュレートされますが、複合材料の界面効果は無視されます。現在、理論モデルでは、球形、円筒形、板状の3つの代表的な電極形状が主に考慮されています。その中で、球形と円筒形は通常1次元モデルであり、プレート電極の1次元モデルと2次元モデルの両方が利用可能です。最近、多くの研究が、リチウムイオン電池のシリコンナノ粒子電極における拡散誘起応力に焦点を合わせています。たとえば、Yang etal。 [5]は、結晶シリコンナノワイヤのリチウム化によって誘発される相変態、形態変化、応力発生、および破壊を調査するための化学機械モデルを提示しました。 Li etal。 [6]は、シリコンナノ粒子電極の拡散誘起応力に対する局所速度の影響を研究しました。趙ら[7]は、ホスト材料の非弾性変形を考慮して、拡散誘起応力を分析しました。これらすべての前述の研究において、関与する基本的な物理学は、複数の駆動力の下での固体における原子またはイオンの拡散です。固体中の原子拡散は、固体組成をその化学量論的状態から変化させ、拡散によって誘発される応力の影響を受ける可能性があります。このような応力と拡散の相互作用は、固体の熱力学的平衡によって支配されます。

LarcheとCahn [8]は、非静水圧応力下で平衡に達する多成分固体の熱力学的フレームワークを開発しました。フレームワークは、組成の変化によって引き起こされる変形が小さく、等方性であるという仮定に基づいていました。その結果、応力と拡散の間の相互作用を説明するために、応力に依存する化学ポテンシャルが導入されました。 Wu [9]は、静水圧コーシー応力の代わりにエシェルビー運動量テンソルが関与する、異なる応力依存の化学ポテンシャルを導き出しました。これに基づいて、Cui etal。[10]固体の有限変形のための新しい化学ポテンシャルを提案しました。ただし、これらの作業では、変形が小さい場合、または拡散に比べて変形率が十分に低い場合にのみ、導出を厳密にする必要があります。シリコン電極は、急速にリチウム化されると組成の体積膨張が大きくなるため（〜400％）、重大なエラーが発生する可能性があります。

この論文では、Cuiの従来の表現とは異なり、低変形速度を想定せずに開発された化学ポテンシャルの表現を提示します[10]。このモデルは、充電または放電中の電極の高速変形のために確立されており、化学ポテンシャルは大量ではなく示強変数であるため、形態に依存しません。応力とLi濃度の分布における化学ポテンシャルのこれら2つの表現の違いは、Siナノ粒子電極の定電位動作と定電流動作の両方で分析されます。結果は、変形速度の増加とともに差が増加することを示しています。化学ポテンシャルのこれら2つの表現によって引き起こされるLiフラックスと、ほとんどのリチウム化プロセス中のコーシー静水圧応力との間に差がない臨界半径が同時に検出されます。

メソッド

機械方程式

リチウムを電極に挿入すると、体積が変化する可能性があります。便宜上、固体の変形と運動を記述する2つの方法、つまりラグランジュ記述とオイラー記述を使用します。連続体媒体内の材料粒子の運動は、

ここで、 x オイラー座標、 X はラグランジュ座標であり、 U は変位フィールドです。連続体の形状の変化は、

ここで、Gradはラグランジアン記述の勾配演算子を表し、 I は2次の単位テンソルです。

球形粒子の場合、材料点のラグランジュ座標とオイラー座標は、球形システムでそれぞれ（R、Θ、Φ）と（r、θ、φ）です。次に、変形勾配テンソル F として見つかります

充電中または放電中の電極の形状変化は、（a）リチウムの挿入による形状変化と（b）可逆的な弾性変形の2つのプロセスに分けることができます。これらの2つの変形プロセスは、2つの分離された勾配テンソルで記述でき、総変形勾配テンソルは次のように記述できます。

ここで、 F ^e 弾性変形を表します F ^c リチウムの挿入による形状変化を表します。式（4）は、電極材料が初期（変形していない）状態から現在の（変形した）状態に至るまでのプロセスを表しています。リチウムの挿入による形状変化が等方性であると仮定すると、 F ^c によって与えることができます

ここで、Ωは部分モル体積を表します。

式から（3–5）、弾性変形勾配テンソル F ^e

総グリーンラグランジュひずみテンソル E

ここで、弾性ひずみテンソル E ^e および拡散誘起ひずみテンソル E ^c

それぞれ。

式を代入します。 （6）式に（8）、Green-Lagrangeひずみテンソルの半径方向および接線方向の成分は

変形の構成関係は、ひずみエネルギー密度から次のように決定できます。

ここで W はラグランジアン記述の弾性ひずみエネルギー密度であり、 P 最初のPiola-Kirchhoff応力です。さらに、材料が線形弾性である場合、 W Green-Lagrangeひずみテンソルの2次関数として記述できます

ここで、 E _h およびν はそれぞれヤング率とポアソン比であり、 C は剛性テンソルであり、det（ F ^c ）は、拡散によって引き起こされる変形の変形勾配テンソルの決定要因です。

最後に、最初のPiola-Kirchhoff応力は

式を組み合わせる（5）、（9）、（10）、および（13）、最初のPiola-Kirchhoff（P-K）応力テンソルの対応するコンポーネントは

そして、最初のP-K応力は、体積力がない場合の平衡条件を満たす必要があります

初期条件と境界条件を使用

物質移動方程式

座標と時間の関数である電極内のリチウムの濃度と拡散流束は、 C と呼ばれます。 （ X 、t）および J （ X 、t）ラグランジアンの説明で、

ここで、Divはラグランジュ記述の発散演算子を表します。球面対称性の特性を考慮すると、拡散は半径方向にのみ発生し、 J を使用します。 （ R 、t） J の半径方向成分を表す （ X 、t）。球系では、式。 （18）は

電極内のリチウムの拡散は、化学ポテンシャル勾配と半径方向のフラックス J によって駆動されます。 （ R 、t）は化学ポテンシャルμの勾配に比例します 、[11]

ここで D は拡散係数、 R _g は気体定数であり、 T は温度です。 μ 濃度に対する総エネルギー密度の偏差として定義され、

システムのエネルギー密度Πは、化学エネルギー密度とひずみエネルギー密度の合計として記述できると仮定します。したがって、総内部エネルギー密度は次のように書くことができます

式を代入します。 （22）式（21）に、化学ポテンシャルμ あることを示すことができます

ここでμ ₀ （ C ）およびτ （ E ^e 、 C ）は、それぞれ化学ポテンシャルの応力に依存しない部分と応力に依存する部分です。そして

ここでμ ₀ は標準状態での化学ポテンシャルを表す定数であり、γ は、原子/分子間の相互作用の影響を表す活量係数です。希薄溶液の場合、原子/分子間の相互作用はごくわずかです。したがって、γ =1。

化学ポテンシャルの応力依存部分に焦点を当てますτ （ E ^e 、C）、これはひずみエネルギー密度 W の導関数です。 リチウムの濃度に関して C。 伝統的に、Π（ X 、t）はヘルムホルツ自由エネルギー密度と見なされるため、このステップは[11]

下付き文字 H これは、ヘルムホルツの自由エネルギー密度が原因であることを意味します。化学ポテンシャルは

ここで、σ _m はオイラー記述のコーシー静水圧応力であり、

剛性 C に注意する価値があります 電極材料の濃度は、リチウムの濃度に依存しないと想定されています C 式で。 （12）。さらに、det（ F ^e ）≈1は広く受け入れられているため、通常は無視されます。この論文の残りの部分では、式を呼び出します。 （26）化学ポテンシャルの伝統的な表現として。一方、Π（ X 、t）は、フェーズフィールドモデルに関するいくつかの研究[12、13]でギブズの自由エネルギー密度であると見なされているため、τの展開された式を取得できません。 （ E ^e 、C）、および

下付き文字 G ギブズの自由エネルギー密度が原因であることを意味します。この場合、μ

そして、式を呼び出します。 （29）化学ポテンシャルの発達した表現として。

物質移動方程式は、方程式で構成されます。 （19）、（20）、（26）、および（29）は、化学ポテンシャルの従来の表現と開発された表現を使用します。この論文の残りの部分では、化学ポテンシャルのこれら2つの表現が、さまざまな帯電方法での拡散誘起応力とLi濃度に及ぼす影響を比較します。

熱力学では、ヘルムホルツ自由エネルギーは、一定の温度と体積で閉じた熱力学システムから得られる有用な仕事を測定する熱力学ポテンシャルです。対照的に、ギブズの自由エネルギーは、一定の温度と圧力で熱力学システムによって実行される可能性のある可逆仕事の最大値を測定します。応力レベルが低い固体では、通常、固体の変形が小さいため、ギブズの自由エネルギーはヘルムホルツの自由エネルギーとほぼ同等です。この仮定は、拡散によって引き起こされる変形が小さいため、ほとんどの固体材料に適していますが、リチウム化中の体積膨張が大きいため、シリコンを除きます。実際、拡散と変形は同時に起こるので、濃度が変化している間に変形が起こらないと仮定することは適切ではありません。それでも、式からわかるように。 （25）、変形速度が十分に低い場合でも、化学ポテンシャルの従来の表現は正確です。ただし、Siナノ粒子電極を急速にリチウム化すると、大きなエラーが発生する可能性があります。

電極は、その表面に一定のリチウムイオン濃度、すなわち定電位動作、またはその表面に一定の流束、すなわち定電流動作でリチウム化されます。式の境界条件。 （19）は

それぞれ。初期条件は次のように記述されます

充電操作ごとに。ここでは、 C _max は材料の最大リチウム濃度であり、 j ₀ は充電電流を表す定数です。

数値の実装

不可能ではないにしても、偏微分方程式からなる上記のシステムの分析解を得るのは非常に困難です。式で（1）–（3）および（13）–（18）では、COMSOLマルチフィジックスソフトウェアを使用して、拡散による応力とリチウム濃度の変化を数値的に計算します。定電位動作と定電流動作の両方でのシリコンナノ電極のリチウム化が、化学ポテンシャルのさまざまな表現で研究されています。シミュレーションで使用されたSiの材料特性と動作パラメータを表1に示します。便宜上、座標、応力、および濃度の対応する無次元置換が図で使用されています。

球状Si電極のさまざまな時点での化学ポテンシャルのさまざまな表現の違いを調べるために、充電状態（SOC）は次のように計算されます。

ラグランジュ記述における応力誘起拡散流束は、

それぞれ、異なる化学ポテンシャル式によって引き起こされるフラックスを表します。

結果と考察

図1は、いくつかのSOCでの定電流動作下での球状Si電極のリチウム濃度、ラジアル応力、およびフープ応力の空間分布を示しています。比較のために、化学ポテンシャルの開発された表現と従来の表現の両方を使用した数値結果が含まれており、それぞれ実線と三角形の記号で表されています。図1aの各SOCについて、実線は三角形の記号とほぼ重なっています。リチウムの濃度に対する化学ポテンシャルの異なる表現によって引き起こされる影響は無視できます。図1bと図1cでは、SOCが46.7％と65.5％の場合、実線は中央の三角形よりも高くなっていますが、他のSOCと同様に、外側はほぼ重なり合っています。全体として、定電流動作下でのリチウム濃度と応力にわずかな影響があります。図2は、いくつかのSOCで定電位動作下にある球状Si電極のリチウム濃度、ラジアル応力、およびフープ応力の空間分布を示しています。図1と図2の両方で、SOCの増加に伴ってラジアル応力とフープ応力が最初に増加し、次に減少することは言及する価値があります。これは、初期状態または完全にリチウム化された状態のシリコン電極に応力がないためです。濃度勾配がないので。図1aと比較すると、図2aでは実線と三角形の差が大きくなっています。表面のリチウム濃度により、一定の C _max 定電位動作下では、帯電率は定電流動作の変形率および変形率よりも高くなります。ただし、同じSOCでの全体の変形は、充電方法に関係なくほぼ同じであり、時間がかかるだけです。化学ポテンシャルの表現の違いによるリチウムの分布への影響は、変形ではなく変形速度にのみ関係し、変形速度の増加とともに増加することを示しています。実際、既存の実験では、特定の充電モードでのリチウム化中にシリコン電極が非常に急速に変形することが示されています。図3 [17]からわかるように、SiアノードはLi金属に対して2Vの電位で1分で完全に変形します。この状態では、化学ポテンシャルのこれら2つの表現によって解決される結果は大幅に異なります。残念ながら、この場合、電極の応力を正確に測定できないため、モデルと定量的に比較することはできません。

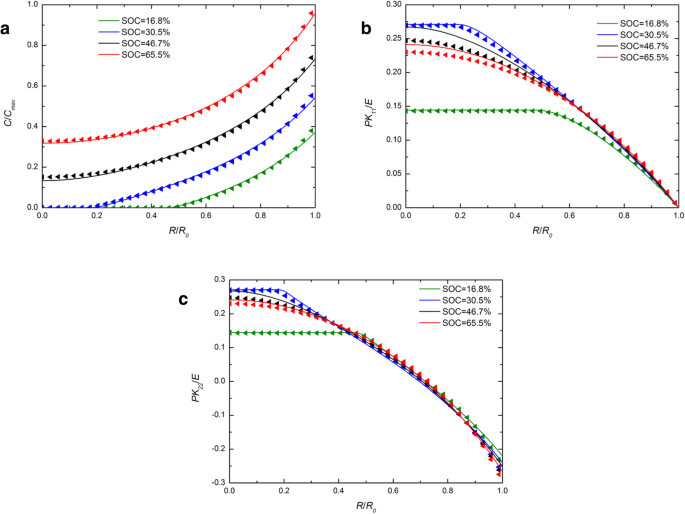
（ a の空間分布 ）リチウムの濃度、（ b ）ラジアル応力、および（ c ）定電流動作下のさまざまなSOCでの球状Si電極のフープ応力（実線は化学ポテンシャルの従来の表現による結果を表し、三角形の線は化学ポテンシャルの発達した表現による結果を表します）

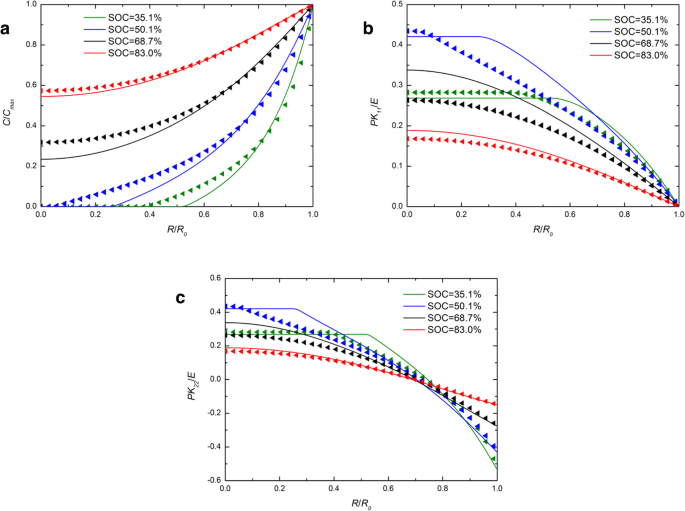
（ a の空間分布 ）リチウムの濃度、（ b ）ラジアル応力、および（ c ）定電位動作下のさまざまなSOCでの球状Siナノ粒子電極のフープ応力（実線は化学ポテンシャルの従来の表現による結果を表し、三角形の線は化学ポテンシャルの発達した表現による結果を表します）

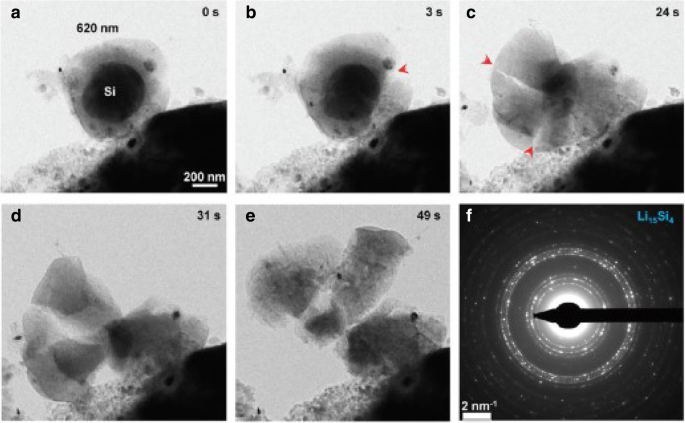
1分間の化学リチウム化中の自立型620nmSiNPの高速変形。 a – e 亀裂の発生と成長の時系列。 f 多結晶Li ₁₅ の形成を示すEDP Si ₄ 完全にリチウム化された相として

図4は、 J の空間分布を示しています。 _H / J _G 異なる j を使用した定電流動作下の異なるSOCでの球状Si電極内 。図4では、実線は三角形とほぼ一致しています。これは、異なる化学ポテンシャル式が J の比率にわずかな影響を与えることを示しています。 _H および J _G 。 J の値の範囲が明らかです _H / J _G 充電電流の増加とともに増加します。これは、電荷電流が大きいほど変形率が高くなり、化学ポテンシャルのさまざまな表現の影響が大きくなるためです。この比率は、常に中央で1より大きく、表面で1未満です。これは、表面の化学ポテンシャルの発達した表現から得られたフラックスが、従来の表現から得られたフラックスよりも大きいことを示唆していますが、中央ではその逆が当てはまります。図4のすべての実線と三角形が1点とほぼ交差していることがわかります。また、電極にどの電流を流しても、交点に対応する比率は常に約1です。これは、フラックスがさまざまな化学ポテンシャル式の影響を受けにくい臨界半径があることを示唆しています。これを化学ポテンシャル独立領域（CIR）と呼びます。明らかに、CIRは常に球形電極の表面近くにあり、充電電流が増加するにつれて表面に近くなります。

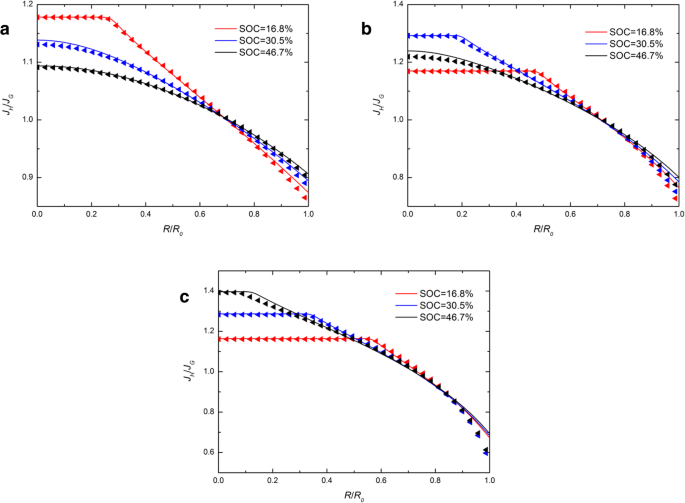
J の空間分布 _H / J _G （ a を使用した定電流動作下のさまざまなSOCでの球状Siナノ粒子電極内 ） j =0.5 j ₀ 、（ b ） j = j ₀ 、および（ c ） j =1.5 j ₀ （実線は化学ポテンシャルの従来の表現による結果を表し、三角形の線は化学ポテンシャルの開発された表現による結果を表します）

式の伝統的な化学ポテンシャルと開発された化学ポテンシャルを比較することによって。 （26）と式。 （29）、コーシー静水圧応力σ _m これら2つの表現の違いの鍵です。 CIRの原因を調査するために、σ _m の空間分布 化学ポテンシャルの表現が異なる定電流動作下の異なるSOCでの球状Si電極の/ Eを図5と図6に示します。明らかに、ほぼすべての曲線がCIRとコーシー静水圧応力σ_{の1点で交差しています。 m} 充電開始時（SOC =6.2％）を除いて、この時点では0に近い値です。 σ _m CIRは、ほとんどの充電期間中、低レベル（ほぼ0）に保たれます。静水圧応力σ _m の場合、2つの化学ポテンシャル式はほぼ同等であると解釈できます。 は0に近いです。これは、CIRが表示される理由を部分的に説明している可能性がありますが、σ _m の曲線の特徴を説明するのに十分ではありません。 。次の調査で解決する必要があります。

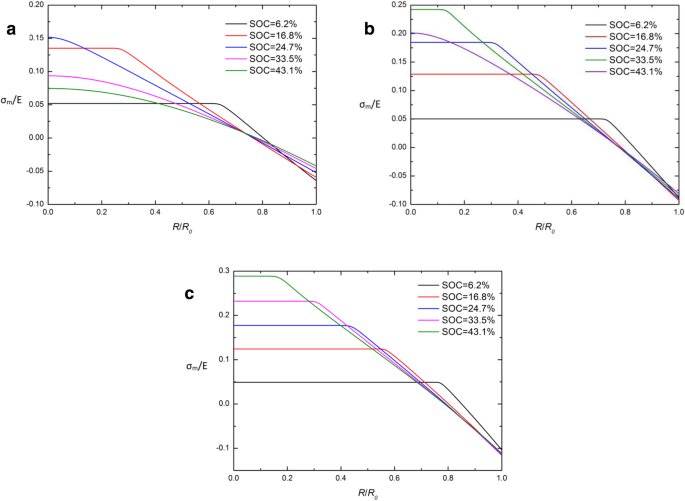
σの空間分布 _m 化学ポテンシャルと（ a の従来の表現による定電流動作下のさまざまなSOCでの球状Siナノ粒子電極の/ E ） j =0.5 j ₀ 、（ b ） j = j _0、 および（ c ） j =1.5 j ₀

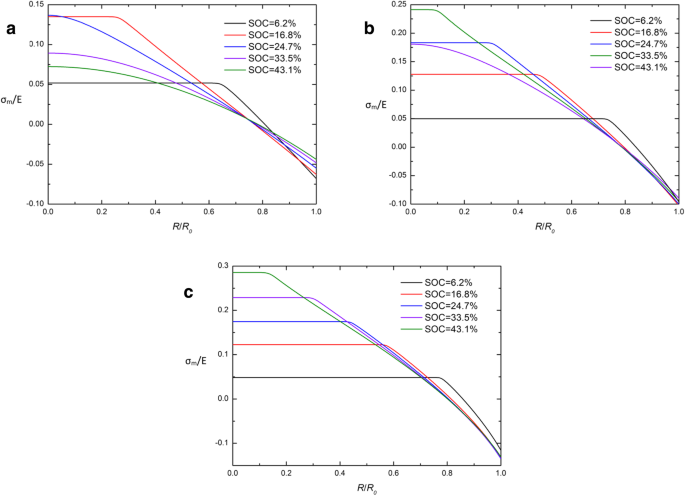
σの空間分布 _m 化学ポテンシャルの発現が発達した定電流動作下のさまざまなSOCでの球状Siナノ粒子電極の/ E（ a ） j =0.5 j ₀ 、（ b ） j = j ₀ 、および（ c ） j =1.5 j ₀ s

結論

この研究では、現在広く使用されている開発された表現とは異なり、低変形速度を仮定せずに化学ポテンシャルの開発された表現を提案します。 Siナノ粒子電極の応力と濃度の分布における化学ポテンシャルの従来の表現と開発された表現の違いは、定電位操作と定電流操作の両方で説明されています。

この結果は、化学ポテンシャルの異なる表現によって引き起こされる影響は、定電流動作では無視できるが、定電位動作では重要であることを示しています。その効果は、変形ではなく変形速度に関係しているだけであり、変形速度の増加とともに大きくなる可能性があることがわかります。従来の化学ポテンシャル式における低変形速度の仮定を考慮すると、開発された化学ポテンシャル式によって得られた結果はより信頼できると考えられます。従来の化学ポテンシャルと開発された化学ポテンシャルによって引き起こされるフラックスがほとんどのリチウム化プロセスでほぼ同じである化学ポテンシャル非依存領域（CIR）は、ナノ粒子電極表面の近くにあります。さらに、CIRは、充電電流の増加に伴って表面に近づきます。同様の現象は、コーシー静水圧応力曲線にも現れます。コーシー静水圧応力σ _m どの化学ポテンシャル式を使用しても、CIRは一定に保たれ、ほとんどの場合CIRで低レベル（ほぼ0）に維持されます。そのような結果はまだ文献に報告されていません。

データと資料の可用性

現在の研究中に分析されたデータセットは、合理的な要求に応じて対応する著者から入手できます。

略語

CIR：

これら2つの化学ポテンシャルの表現によって引き起こされる拡散流束がほぼ同じである領域