シリーズR、L、およびC

次の回路例を見て分析してみましょう。

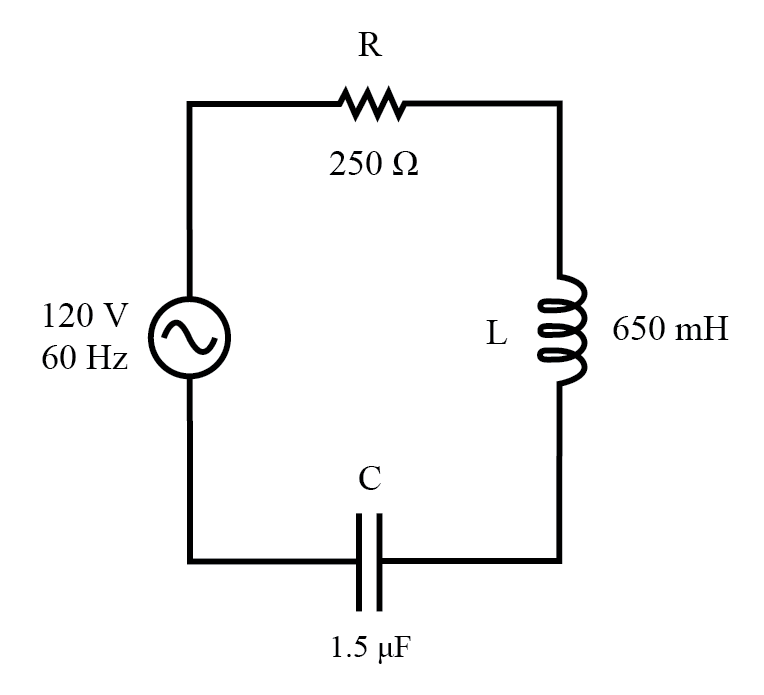
シリーズR、L、C回路の例。

リアクタンスの解決

最初のステップは、インダクタとコンデンサのリアクタンス（オーム）を決定することです。

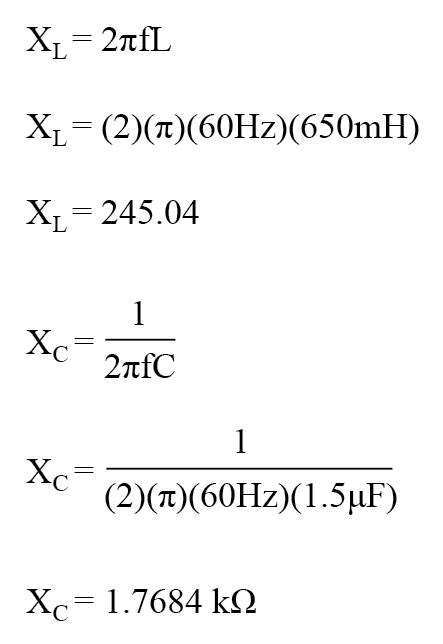
次のステップは、すべての抵抗とリアクタンスを数学的に一般的な形式で表現することです：インピーダンス。 （下の図）

誘導性リアクタンスは正の虚数インピーダンス（または+ 90°のインピーダンス）に変換され、容量性リアクタンスは負の虚数インピーダンス（-90°のインピーダンス）に変換されることに注意してください。もちろん、抵抗は依然として純粋に「実際の」インピーダンス（極角0°）と見なされます：

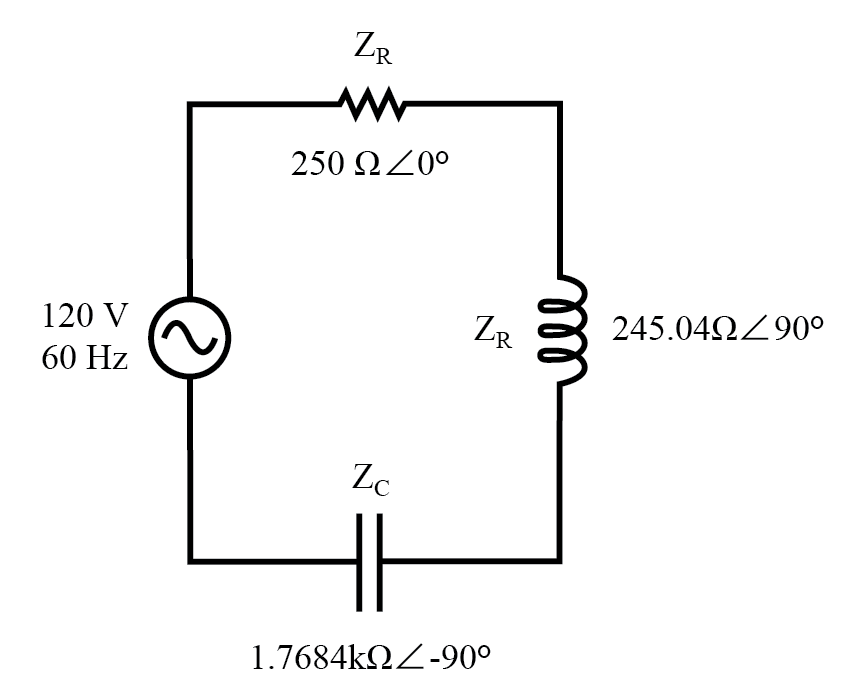
コンポーネント値がインピーダンスに置き換えられたシリーズR、L、およびC回路の例。

結果の集計：

現在、電流に対するすべての量が共通の複素数形式で（抵抗やリアクタンスではなくインピーダンスとして）表現されているため、DC回路の単純な抵抗と同じように処理できます。

これは、この回路の分析テーブルを作成し、すべての「与えられた」数値（合計電圧、および抵抗、インダクタ、コンデンサのインピーダンス）を挿入するのに理想的な時期です。

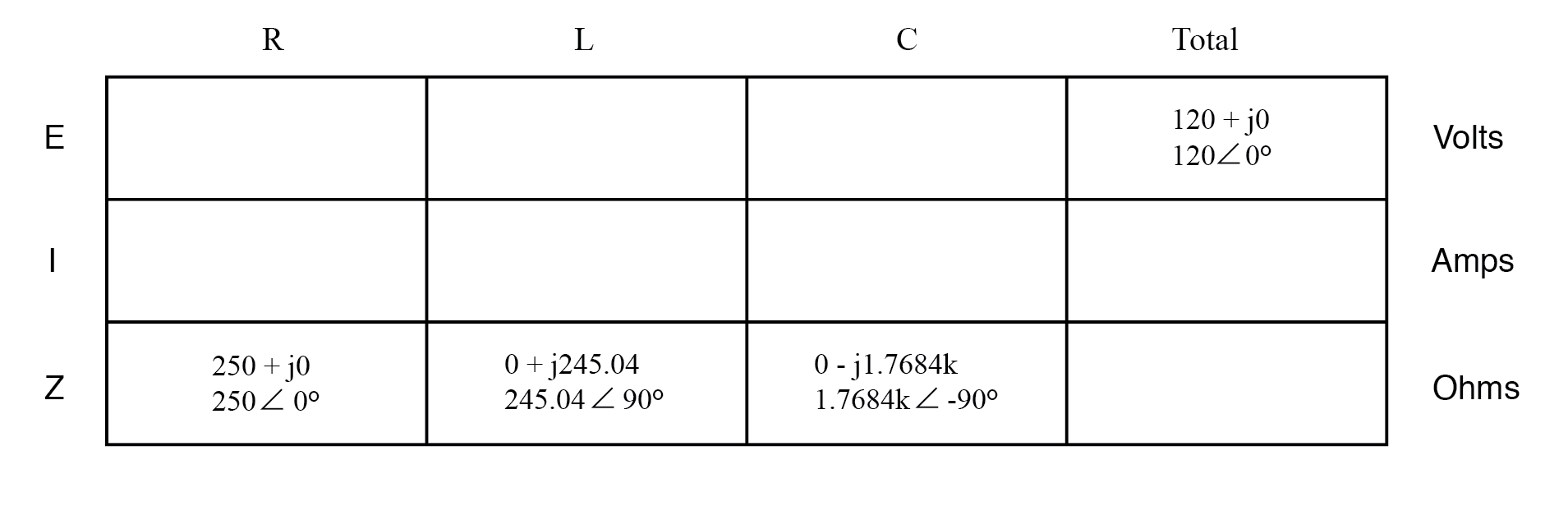
特に指定のない限り、電源電圧は位相シフトの基準となるため、0°の角度で書き込まれます。電圧または電流の位相シフトの「絶対」角度などは常に存在しないことを忘れないでください。これは、常に別の波形に対する相対的な量であるためです。

ただし、インピーダンスの位相角（抵抗、インダクタ、コンデンサの位相角など）は、各コンポーネントの電圧と電流の位相関係が絶対的に定義されているため、絶対的にわかっています。

インピーダンス位相角がそれぞれ正確に+ 90°と-90°の完全に無効なインダクタとコンデンサを想定していることに注意してください。

実際のコンポーネントはこの点で完璧ではありませんが、かなり近いはずです。簡単にするために、特に明記されていない限り、計算例ではこれから完全にリアクティブなインダクタとコンデンサを想定します。

上記の回路例は直列回路であるため、回路の総インピーダンスは個体の合計に等しいことがわかります。したがって、次のようになります。

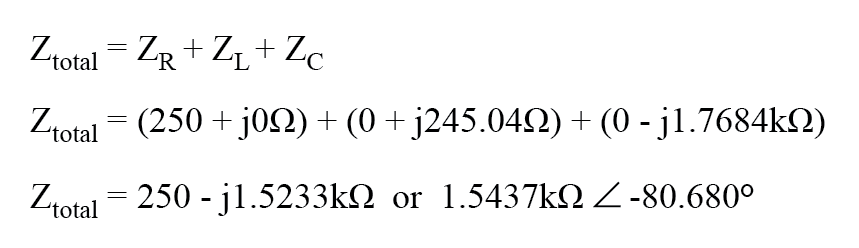
総インピーダンスのこの数値を表に挿入します：

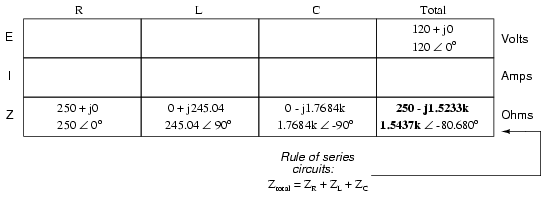
これで、「合計」列にオームの法則（I =E / R）を垂直に適用して、この直列回路の合計電流を見つけることができます。

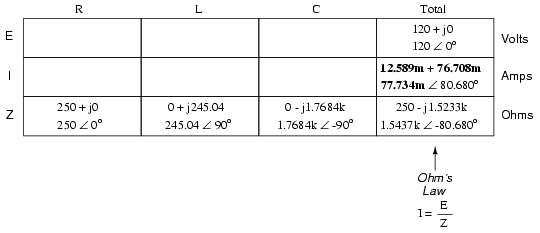
直列回路であるため、電流はすべてのコンポーネントで等しくなければなりません。したがって、総電流について得られた数値を取得し、それを他の各列に分配することができます。

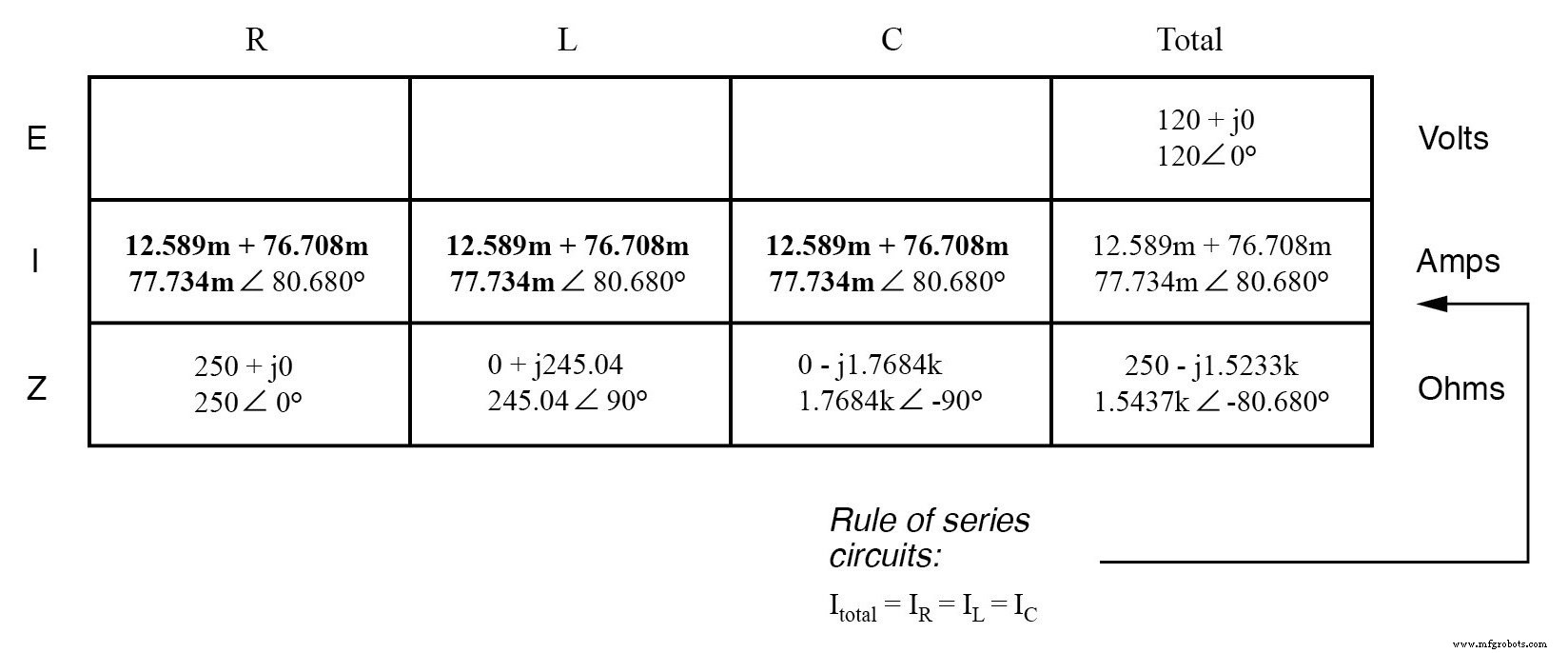
これで、電圧降下を決定するために、表の個々のコンポーネント列のそれぞれにオームの法則（E =IZ）を適用する準備が整いました。

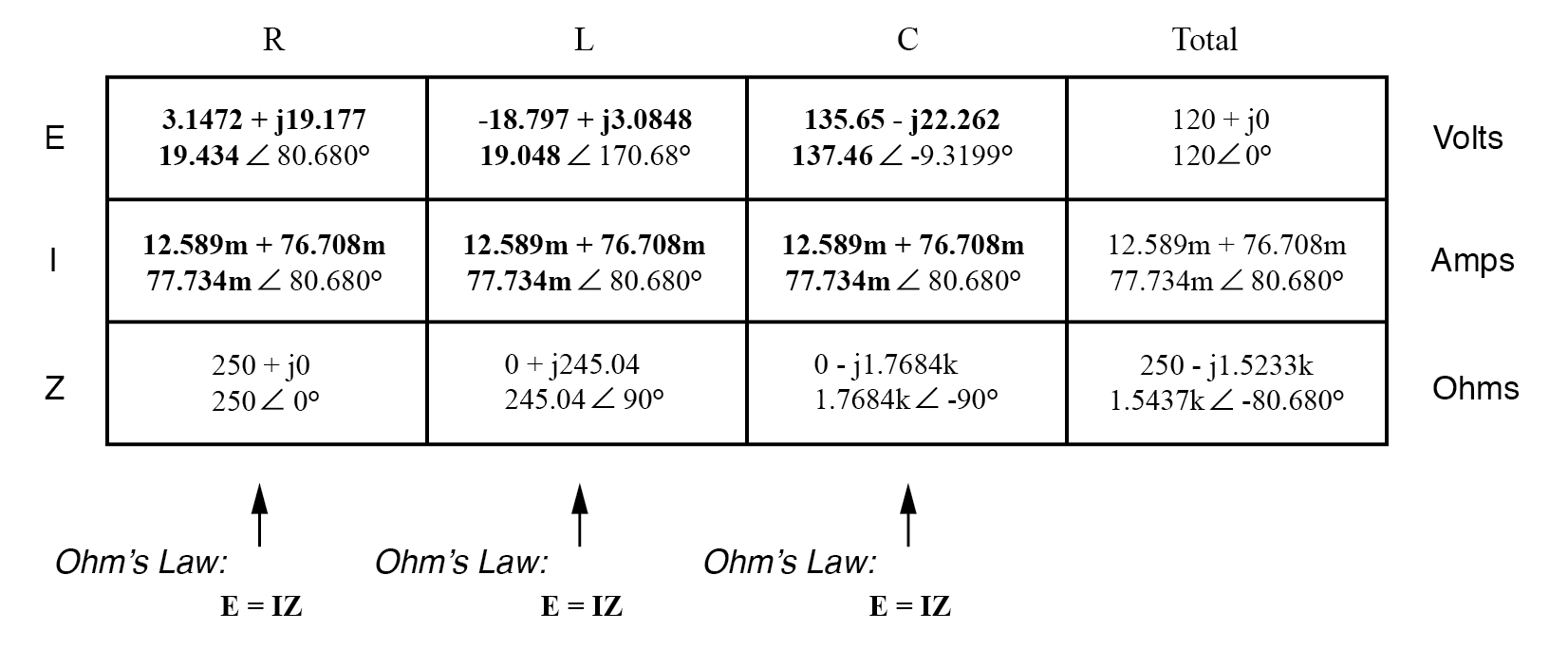
ここで奇妙なことに注意してください。供給電圧はわずか120ボルトですが、コンデンサの両端の電圧は137.46ボルトです。どうすればいいの？答えは、誘導性リアクタンスと容量性リアクタンスの間の相互作用にあります。

インピーダンスとして表すと、インダクタがコンデンサとは正反対の方法で電流に対抗していることがわかります。長方形で表現すると、インダクタのインピーダンスには正の虚数項があり、コンデンサには負の虚数項があります。

これらの2つの反対のインピーダンスが（直列に）追加されると、それらは互いに打ち消し合う傾向があります！それらはまだ一緒に追加されています 合計を生成するには、その合計は実際には少ない 個々の（容量性または誘導性）インピーダンスのいずれか単独よりも。

これは、正と負（スカラー）の数値を足し合わせるのに似ています。合計は、どちらかの個々の絶対値よりも少ない量です。

誘導性要素と容量性要素の両方を備えた直列回路の合計インピーダンスが、どちらかの要素の個別のインピーダンスよりも小さい場合、その回路の合計電流は大きい必要があります。 そこに誘導性または容量性要素のみがある場合よりも。

各コンポーネントを流れるこの異常に高い電流により、個々のコンポーネントの一部でソース電圧よりも高い電圧が得られる可能性があります。同じ回路内のインダクタとコンデンサの反対のリアクタンスのさらなる結果については、次の章で説明します。

すべてのコンポーネント値をインピーダンス（Z）に減らす手法を習得すると、処理される量がスカラーではなくベクトルであることを除いて、AC回路の分析はDC回路の分析とほぼ同じくらい困難になります。

電力（P）を扱う式を除いて、AC回路の式はDC回路の式と同じで、抵抗（R）の代わりにインピーダンス（Z）を使用します。オームの法則（E =IZ）は今でも当てはまり、キルヒホッフの電圧と電流の法則も当てはまります。

AC回路でのキルヒホッフの電圧法則を示すために、最後の回路でのコンポーネントの電圧降下について導き出した答えを見ることができます。 KVLは、抵抗、インダクタ、およびコンデンサの両端の電圧降下の代数和が、ソースからの印加電圧と等しくなるはずであることを示しています。

これは一見真実ではないように見えるかもしれませんが、少し複雑な数の加算はそうで​​はないことを証明します：

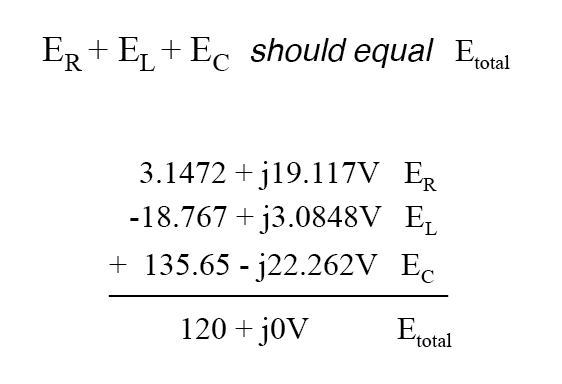
少しの丸め誤差は別として、これらの電圧降下の合計は120ボルトに等しくなります。電卓で実行すると（すべての桁を保持）、受け取る回答は正確にである必要があります。 120 + j0ボルト。

SPICEを使用して、この回路の数値を確認することもできます。

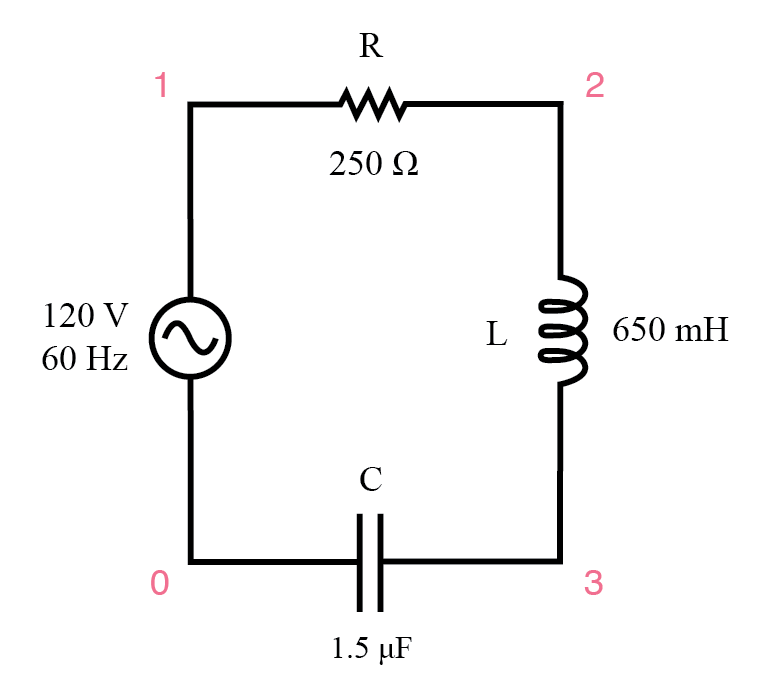
シリーズR、L、CのSPICE回路の例。

 r1 1 2 250 l1 2 3 650m c1 3 0 1.5u .ac lin 1 60 60 .print ac v（1,2）v（2,3）v（3,0）i（v1） .print ac vp（1,2）vp（2,3）vp（3,0）ip（v1） 。終わり 周波数v（1,2）v（2,3）v（3）i（v1） 6.000E + 01 1.943E + 01 1.905E + 01 1.375E + 02 7.773E-02 freq vp（1,2）vp（2,3）vp（3）ip（v1） 6.000E + 01 8.068E + 01 1.707E + 02 -9.320E + 00 -9.932E + 01 

SPICEシミュレーションでは、手動で計算した結果が正確であることが示されています。

ご覧のとおり、電圧、電流、抵抗のすべての量（実際にはインピーダンス）を除いて、AC回路解析とDC回路解析の間にほとんど違いはありません。 ）位相角を考慮して、スカラー形式ではなく複雑な形式で処理する必要があります。

これは、DC電気回路について学んだことすべてが、ここで学んでいることに当てはまることを意味するため、良いことです。この一貫性の唯一の例外は、力の計算です。これは非常にユニークであるため、その主題だけに専念する章に値します。

レビュー：

• あらゆる種類のインピーダンスが直列に追加されます：Z _合計 =Z ₁ + Z ₂ +。 。 。 Z _n
• インピーダンスは直列に追加されますが、直列の誘導性インピーダンスと容量性インピーダンスは互いに打ち消し合う傾向があるため、インダクタンスと容量の両方を含む回路の合計インピーダンスは、個々のインピーダンスの1つ以上よりも小さい場合があります。これにより、コンポーネント間の電圧降下が供給電圧を超える可能性があります！
• 値がスカラーではなく複素数で表現されている限り、DC回路のすべての規則と法則がAC回路に適用されます。この原則の唯一の例外は、パワーの計算です。 、これはACでは大きく異なります。

関連ワークシート：

• 直列-並列組み合わせAC回路ワークシート