抵抗回路図:接続と機能について

抵抗器の回路図について，抵抗器は電子機器の最も重要な電子部品の 1 つです。それらは、電流の流れを制限し、特定の電圧降下を提供し、回路の電気負荷として機能する受動部品です。

これらの目標を達成するために、さまざまな方法で抵抗器の構成を作成できます。直列接続の 3 つの主要な抵抗器、並列接続の抵抗器、および直列接続と並列接続の抵抗器の組み合わせがあります。

この記事では、3 つのタイプすべてについて、それらがどのように機能するかを示す図で説明します。始めましょう!

<オール>

直列接続の抵抗器

直列接続の抵抗器は、端から端まで接続された 2 つ以上の抵抗器を持ち、それらすべてに同じ電圧がかかります。

抵抗器を直列に接続する方法

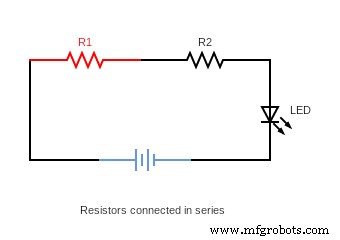
ワイヤの抵抗が無視できると仮定して、各抵抗の両端を電源出力ソースに接続します。抵抗器は直列に接続されているため、一方の抵抗器の抵抗が R1 の場合、もう一方の抵抗器の抵抗も R2 になります。総抵抗は、 の合計です 個々の抵抗器の値;この場合、計算にはオームの法則を使用します。

直列抵抗回路におけるオームの法則

オームの法則によれば、電流は任意の導体の 2 点間の電圧に正比例します。私たちの場合、抵抗器です。

下の図には、一連の抵抗器を接続した単純な回路があります。最初の抵抗器の抵抗値は R1 で、2 番目の抵抗器の抵抗値は R2 です。

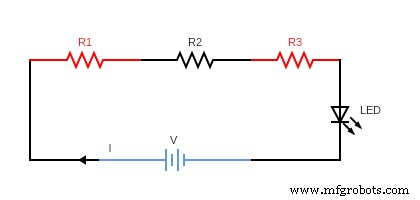
オームの法則によると、 V=IR

V =私 * R_t

ここで R_t は、回路に接続されている抵抗器の実効抵抗です。抵抗回路の両端の電源電圧 (V) は電圧と同じです。さらに、抵抗器は直列に接続されているため、同じ電位降下があります。オームの法則を使用してこの値を見つけることもできます。

直列回路の電流と電力

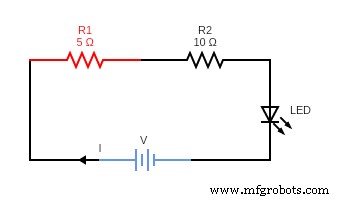
(直列抵抗回路)

直列抵抗回路では、全電流 (I) はすべての抵抗で同じです。つまり、抵抗器 1 を流れる電流は、抵抗器 2 を流れる電流と同じです。また、現在の出力はバッテリーによって提供されるものと同じです。重要なのは、回路に抵抗を追加すると、現在の値が途中で減少することです。抵抗器は、抵抗値の違いにもかかわらず、電流量を均等に分担しているからです。

だから、現在; I_t =I_1=I_2.

同様に、電流、私も =V/Rt

つまり、印加されたバッテリー電圧 (V) を実効抵抗 (Rt) で割ったものです。

電力は式で与えられます。 P=V*I

直列回路では、適用される電位差は、各抵抗の個々の電圧の合計です。

したがって、電力を計算するときは、 P=V_total*I_total

直列回路の実効抵抗

等価抵抗とは、単一の抵抗器がコース内に存在する抵抗器の集合体の全体的な効果と等しくなるために必要な抵抗の量です。

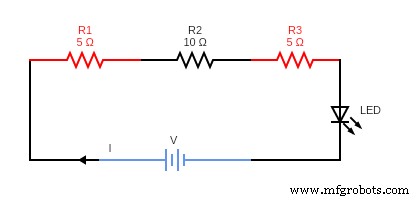
単純な直列回路では、抵抗の合計は個々の抵抗の値の合計に等しくなります。明確にするために、抵抗値を合計します。ただし、抵抗器にも同じ電位降下があります。 たとえば、上記の回路では、実効抵抗式は次のように与えられます;

Rtotal =R1 + R2 + R3

R_t =5Ω+ 10Ω+ 5Ω=20Ω

適用例

LED 電流制限

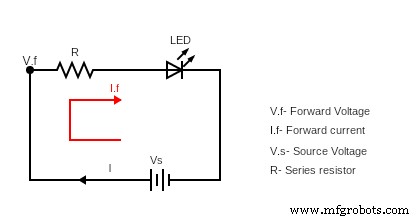
(LED 電流制限回路図)

LED の定格電流は異なります。したがって、それぞれがその定格以下の電流を必要とします。そうしないと、回路に過大な電流が流れると、それらが損傷または破壊されます。それは危険であり、コンポーネントの損傷やさらに悪いことに、火災の原因となる可能性があります!したがって、直列抵抗接続を使用して電気回路を保護することをお勧めします。直列抵抗は LED 全体の最大電圧降下を制限し、安全な動作条件内での動作を維持します!

並列接続の抵抗器

並列接続の抵抗器の場合、すべての抵抗器の一方の端が標準ワイヤを介して取り付けられます。同様に、他のすべての端は標準のワイヤを介して接続されます。

抵抗を並列接続する方法

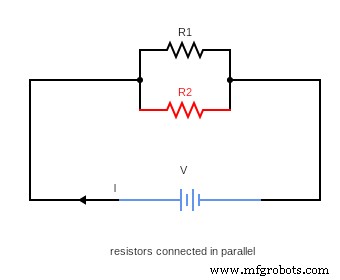
(並列に接続された抵抗器の図)

上記の例では、抵抗器を並列接続した単純な回路があります。抵抗器の並列接続は、各抵抗器の端が電源に接続されておらず、代わりに共有接続として 1 つのポイントを共有するため、異なります。また、ワイヤの抵抗は無視できると仮定します。

抵抗回路図– 並列抵抗回路におけるオームの法則

オームの法則を使用して、各抵抗を並列に流れる個々の電流を見つけます。これは、各抵抗の両端での電位降下が等しいためです。出力電圧が各抵抗の両端で一定の場合、電流 I=V/R

抵抗回路図– 並列回路の電流と電力

並列構成回路の抵抗器の場合、並列分岐間の電圧降下は同じです。また、回路全体に流れる電流は、各抵抗器を流れる個々の電流の合計と同じです。ただし、回路に抵抗を追加すると、回路全体の抵抗が減少します。

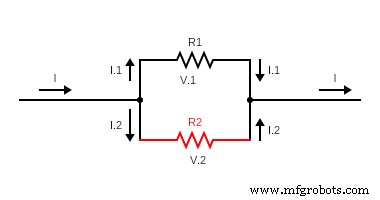
(並列接続での電流分割)

共有される合計電流は各抵抗で分割されるためです。

したがって、現在の方程式を適用します I_t=I_1+I_2

つまり、回路を流れる総電流は、抵抗器を流れる追加の分割電流に等しい.

抵抗によって消費される総電力は、P=VI を使用して求められます。ここで、I は総電流 (アンペア) で、V は並列の各抵抗の両端の電圧です。抵抗値が最も大きい抵抗器は最も低い電流を受け取り、個々の抵抗値が最も小さい抵抗器は最も優れた電流を受け取ります。

したがって; P=VI

P =(I_1 + I_2) * V

したがって、各抵抗器について、抵抗器 R_1 I1=V1/R1.抵抗 R_2 I2=V2/R2

並列回路の実効抵抗

下の図は、並列回路で実効抵抗を見つける方法を説明するのに役立ちます.

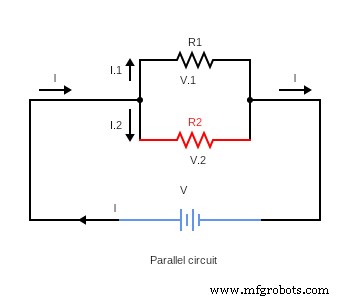
(実効抵抗を説明する模式図)

等価抵抗を計算するには、キルヒホッフのループ法則に従ってジャンクション ルールを理解する必要があります。 並列構成回路の総抵抗は、すべての逆抵抗の合計の逆数です。つまり、並列接続に 2 つの抵抗がある場合、実際の抵抗の計算は次のようになります。

回路方程式は次のとおりです。

電流は接合部で分岐するため、ループ ルールに従って、I=I1+I2

そして、V=I1R1 および I1R1=I2R2 であるため

次に、電流 I =I_1+ I_2

=V1/R1+ V2/R2

しかし V は同じ =V/R1+ V/R2

=V[ 1/R1+ 1/R2] =V/要求

1/必須 =1/R1+ 1/R2

また、Eq Resistance Req=[1/R1+ 1/R2]⁻¹

抵抗器の直列接続と並列接続の組み合わせ

抵抗器の組み合わせでは、一部の抵抗器は直列構成ですが、他の抵抗器は並列構造になっています。

最も重要なことは、これらがさらに 理解する複雑な回路。組み合わせ回路で抵抗を見つけるという中心的な概念は、コース全体を直列接続回路に変換することです。これは、並列回路における等価抵抗の理解を結合回路全体に適用することによって迅速に行われます。

抵抗回路図– 抵抗器を直列と並列に組み合わせる方法

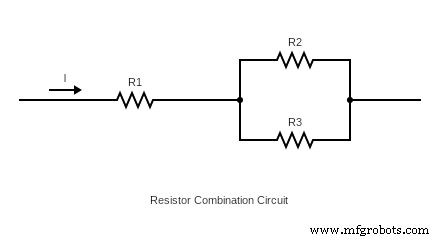
(抵抗組み合わせ回路)

直列と並列の抵抗を組み合わせるのはとても簡単です。まず、R2 と R3 を並列に接続するだけです。次に、各抵抗器の両端をクリックしてノードを作成します。ここで、上の図のように、別の抵抗 R1 を接続ノードに追加します。最後に、ワイヤの端を電源に接続します。合計抵抗は、各抵抗の値の合計です。この場合、計算にはオームの法則を使用してください。

抵抗回路図– 直列抵抗回路と並列抵抗回路の組み合わせにおける電流と電力

総電流はすべての個々の電流の合計であり、電力も同様です。複数の抵抗が並列に接続されている場合、それらは共通の出力電圧源を共有します。重要なのは、これが があると仮定します ごくわずかな内部抵抗。また、各抵抗の両端の電圧が、直列の場合よりも小さくなることも意味します。

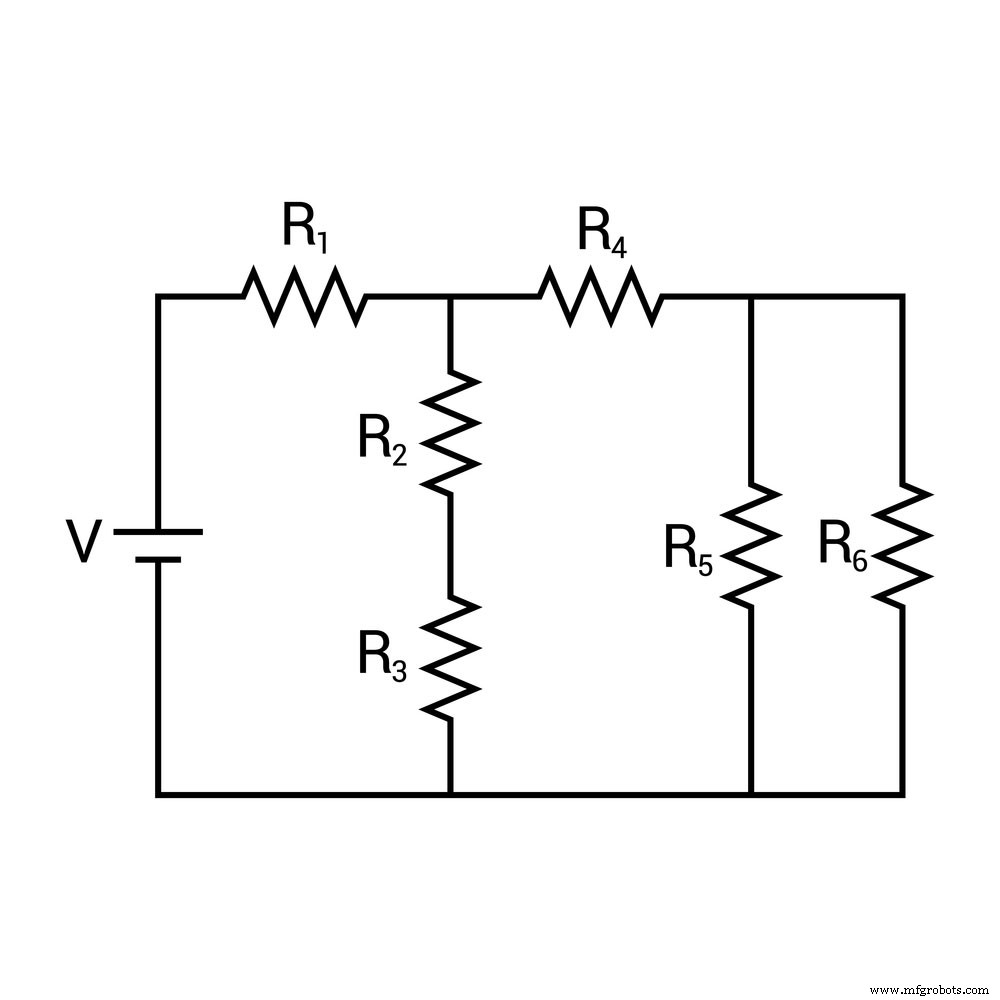
(直列および並列の抵抗器)

直列と並列の両方で抵抗器の組み合わせがある場合は、さまざまな電圧と電流の分割を使用する必要があります。理解するのは複雑な関係であることを忘れないでください。

オームの法則を組み合わせた形式を使用して、総出力電流を求めます。ここで、I=V/R_total です。

これは、接続された抵抗がそれらの間で電流を共有することを意味します。

総電力は直列と同じですが、各抵抗器が消費する電流と電圧は少なくなります。

P=VI =(Vsource/R_total) * I

抵抗回路図– 直列および並列回路の実効抵抗

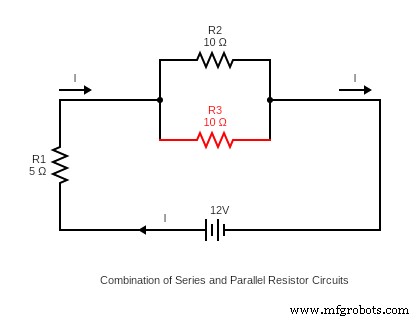
(直列抵抗回路と並列抵抗回路の組み合わせ)

抵抗の組み合わせの等価抵抗は、それらの値と接続方法によって異なります。したがって、さまざまな直列および並列抵抗回路の総抵抗は、オームの法則を使用して求められます。

まず、R_total =Req(シリーズ) + Req(パラレル)

次に、Req parallel=Req₂₃=(1/R2+ 1/R3)⁻¹

=(1/10Ω+1/10Ω)⁻¹ =5Ω

次に、並列の抵抗器 2 と 3 が R1 と直列になります。

したがって、R-total=Req(シリーズ) + Req(パラレル)

Rt=5 Ω+ 5Ω=10Ω.

抵抗器を直列と並列に組み合わせることで、電気負荷の電位降下を制限しながら電流を制御できます。

抵抗回路図 - 応用例

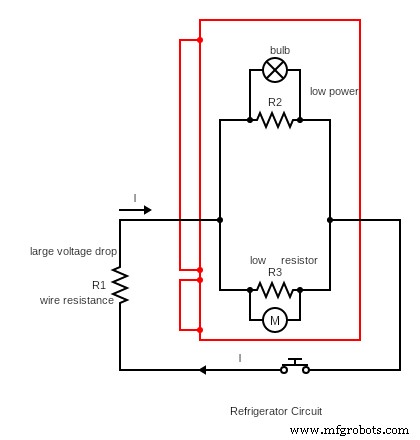
(冷蔵庫回路図)

冷蔵庫回路では、抵抗回路の組み合わせが存在します。上の図では、冷蔵庫のドアが開くと電球が暗くなります。これは、冷蔵庫のモーターが大電流を消費するためです。その結果、電球は低電力を受け取るため、回路内のR1で大きな電圧降下が発生すると暗くなります.抵抗の組み合わせは、回路を通過する電流の最大量を制限するのに役立ちます。同時に、電気負荷全体で特定の潜在的な削減を提供します。

まとめ

結論として、最も一般的な 3 つのタイプの抵抗回路図について説明しました。さまざまな接続タイプとその仕組みについて理解を深めていただければ幸いです。

これで、抵抗回路を設計できます。これを行う方法についてさらに質問がある場合は、お問い合わせください。