ナノカーボンフィラーの電界支援配向による複合材料の電気的性質

背景

調整可能な特性は、電子および構造部品として多くの産業で導電性炭素ベースの複合材料のアプリケーションを提供します：マイクロエレクトロニクス、静電散逸、電磁シールド製造、航空機構造など[1,2,3,4]。それらは金属のように腐食しませんが、さまざまなフィラーが使用されているため、適切な強度、重量、および広範囲の導電率値を備えています。

非球形粒子は、複合材料の導電性を改善するという観点から、複合材料フィラーとしてより有利です[5、6、7]。これは、統計的パーコレーションモデルのパラメータである粒子アスペクト比[8]の増加時に充填率の値が低くなるためです。したがって、アスペクト比の値が高い（10 ¹ ）ことを特徴とするカーボンナノチューブ（CNT）とグラファイトナノプレートレット（GNP）を備えた複合材料の開発 –10 ⁴ ）[9]は、フィラーとして、非常に有望な方向性です。幾何学的異方性に加えて、CNTとGNPは物理的特性の異方性によって区別されます。しかし、複合材料でのフィラーのランダムな分布では、個々のフィラー粒子の異方性が補償されます。さらに、ランダムなフィラー分布では、その多くは、ネットワーク全体から切り離された導電性ネットワークのいわゆる「ブランク」ブランチに集中します。これらの損失は、複合材料のフィラー含有量が少ない場合に特に顕著になります。

フィラーとその特定の空間分布を再構成することで、パーコレーションのしきい値が低い複合材料を得ることができ、材料のコストを削減できます。異方性フィラー分布を持つ複合材料の最も一般的な調製方法は、液体複合材料混合物を電磁界にさらすことと機械的応力を加えることです。圧延によるフィラー配向法の不利な点の中で、せん断応力は、そのような曝露下でカーボンナノ粒子の破壊と破壊の可能性があります[10]。磁場によって引き起こされる整列には、複合材料に磁性成分を追加する必要があります[11]。したがって、複合材料中のフィラーの電界支援アライメントは、多くの研究グループの観点から、異方性複合材料形成の最も有望な方法です[12、13]。

しかし、電界支援配向に関する提示された研究の圧倒的多数は、ポリマーマトリックスに埋め込まれたカーボンナノチューブに専念しています[14、15、16、17、18]。配向プロセスに対するフィラー粒子の形態の影響は、理論的研究と実験的研究の両方でほとんど開発されていません[19、20、21]。この研究の目的は、整列した複合材料形成のプロセスに対するフィラーの形態の影響を調査し、ランダムで整列したGNP分布を持つ複合材料の電気伝導率の濃度依存性の違いを特定して説明することでした。

メソッド

資料

エポキシ樹脂Larit285（Lange Ritter GmbH、ドイツ）に基づいて、複合材料が製造され、この研究で調査されました。初期状態では、このポリマーは2成分であり、液体エポキシと適切な硬化剤H 285で構成されています。使用済み樹脂の低粘度（25°で600÷900 mPa×s）および硬化剤（50÷100 mPa×s） 25°С）は、複合材料の製造に外部電界の影響を利用することを可能にします。

製造された複合システムのフィラーとして、次の材料が使用されました。

• 多層カーボンナノチューブ（MWCNT）（Cheap Tubes Ins、USA）;

• グラファイトナノプレートレット（GNP）。

ＧＮＰは、分散したグラファイトの深い熱化学処理の結果として生じる生成物である熱的に剥離したグラファイトの超音波分散（アセトン媒体中で３時間）によって得られた。 GNP製造のプロセスは、[22]で詳細に説明されています。

表1に、使用したフィラーのパラメーターを示します。それらの寸法と形状は、私たちの研究グループの論文でAFM、SEM、および光学顕微鏡を使用して推定されました[23、24]。 GNP粒子とMWCNT粒子は、形状、サイズ、したがってアスペクト比によって区別されます。表1は、最大、最小、および平均の粒子の特性パラメータを示しています。粒子は、アスペクト比の値によって「最大」、「最小」、および「平均」とマークされます。粒子の質量を評価すると、密度ρ （MWCNT）=1.8 g / cm ³ [25]、ρ （GNP）=2.23 g / cm ³ 、単結晶グラファイトの密度として。

複合材料の製造

調製された複合サンプルには、フィラーとしてさまざまな濃度のGNPが含まれていました（0.05、0.5、0.7、1、2、3、4、5 wt％）。あるタイプのサンプルではフィラーがランダムに分布しており、別のタイプでは、GNPは外部電界によって整列されていました。

複合システムの作成方法は以下のとおりです。最初に、必要な量のカーボンフィラーを事前に溶解したポリマーマトリックスに注ぎ、機械的に混合しました。その後、混合物を超音波分散にさらして、エポキシマトリックス中のフィラーのより良い分布を得た。分散は、周波数40 kHz、最大出力電力50 Wの超音波浴Вaku-9050で行いました。複合混合物を50Wで30分間超音波作用にさらし、その後、硬化剤Н285を得られた複合材料に添加しました。 Larit285の重量に対する質量比100/40の混合物。

最終的に、充填剤の分布が整列した複合材料の場合、得られた複合材料の混合物の一部を、コンデンサーのプレートの間に配置されたプラスチックの型に流し込みました。周波数15kHz、マグニチュード2000VのAC電圧をプレートに印加しました。電界源として、周波数15 kHz、マグニチュード2000 VまでのAC電圧、またはマグニチュード2000VまでのDC電圧を発生させる高電圧源を使用しました。電界の大きさの値は、ユニバーサル電圧計В7-16Аによって制御されました。

AC電界周波数を選択する際には、次の2つの点に留意しました。（1）周波数は、カーボンナノ粒子の整列時間がエポキシ硬化の時間になるように十分に高くする必要があります。 （2）周波数は、電場でのナノ粒子配列のダイナミクスを観察するのに十分低くなければなりません。これらの考慮事項を念頭に置いて、15kHzの周波数で複合材料の形成を実行しました。

複合混合物の他の部分は、外部電界の影響を受けずに残されました。

室温で保持した後、複合材料サンプルを含む金型を、40°Cから80°Cまで段階的に上昇する温度で熱処理し、10°Cで1時間ごとに上昇させました。これは、複合材料の重合プロセスを完了するために行われました。

光学顕微鏡

電界処理下のエポキシマトリックス中のカーボンフィラー分布の特性の調査は、0.05 wt％のカーボンフィラーの含有量を持つ複合材料に対して実行されました。これは、デジタルカメラEtrekDCM-510を備えた立体光学顕微鏡МBS-1を使用して行われました。この設定により、電界の影響下でカーボンナノ粒子が分散した液体エポキシをオンラインで観察する機会が得られました。実験の構成については、[26、27]で詳しく説明されています。 MWCNTs /-およびGNPs / Larit 285複合材料の一連の光学的観察は、15 kHzのAC電圧またはDC電圧を電極に供給し、電界の大きさの値を変更してリアルタイムで実施されました。

電気的特性の測定

調査した複合材料の電気伝導率は、室温でDCモードの標準的な2プローブ法によって測定され、電気抵抗の測定限界は10 ¹⁰ でした。 オーム。 10 ¹⁰ より高い オーム、抵抗はteraommetrЕ6–13を使用して測定されました。測定用のサンプルは、5.0×4.0×4.0 mm ³ の寸法の通常の平行六面体の形で準備されました。 。

モデリング

電界作用下での炭素粒子の回転の特徴的な時間を推定する方程式は、数学パッケージMaple13を使用して解かれました。

結果と考察

光学的観察

次の図は、アクションでの低フィラー含有量（0.05 wt％）の複合材料GNP / Larit 285（図1および2）およびMWCNT / Larit 285（図3および4）[26]の表面の光学写真を示しています。 AC電界の。

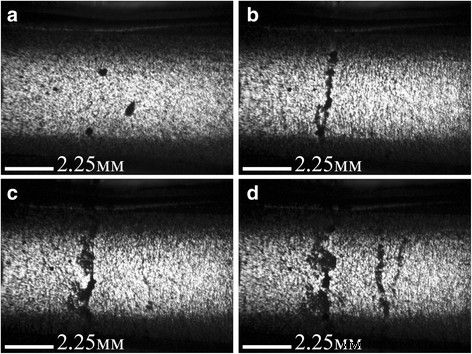
強度36kV / m、周波数15 kHzのAC電界作用下での0.05 wt％GNP / Larit 285複合材料の電気的「絶縁破壊」形成の光学画像（埋め込み電極）： a -電界作用の前。 b -100秒後; c -140秒後。 d —160秒の電界作用後。画像サイズ10.8×8.0mm ²

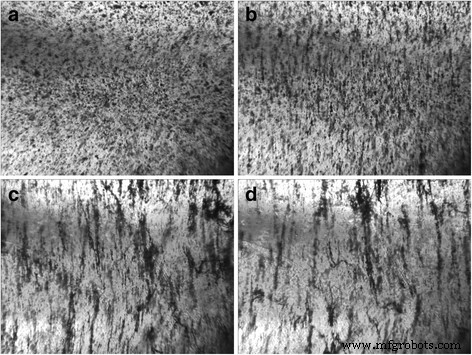
AC電界作用（周波数15 kHz、強度167 kV / m）下での0.05 wt％GNPs / Larit 285複合材料の光学画像（コンデンサー内）： а— 電界作用の前; b -12分後。 c —26分後。 d —60分の電界作用後。画像サイズ10.8×8.0mm ²

AC電界作用（周波数15 kHz、強度83.3 kV / m）下での0.05 wt。％MWCNTs / Larit 285複合材料の光学画像（埋め込み電極）： a –電界作用の前。 b –12分後。 c –26分後。 d –電界作用の60分後。画像サイズ10.8×8.0mm ² [26]

AC電界作用（周波数15 kHz、強度50 kV / m）下での0.05 wt％MWCNTs / Larit 285複合材料の光学画像（埋め込み電極）：а -電界作用の前。 b -12分後。 c —26分後。 d —60分の電界作用後。画像サイズ10.8×8.0mm ² [26]

AC電界で処理されると、外部電界の電力線の方向へのフィラーの移動により、電界作用の時間が長くなるにつれて、複合材料はより透明になりました。電界作用の時間が長くなるにつれて、カーボンフィラーの整列した構造が広がり、それらの間にいくらかのクリアランスが現れることも観察された。これは、カーボンナノ粒子のファンデルワールス相互作用が原因である可能性があります。このようにして、特定の分布のナノカーボンフィラーの鎖が複合材料で形成されています。

図1に示すように、埋め込み電極構成のGNP / Larit 285複合材料の場合、AC電界作用は、外部電圧電極による供給を閉じ、高振幅の電流が流れる主な導電経路の作成に現れます。複合サンプル。したがって、Larit 285でのGNPの位置合わせは、複合材料がコンデンサのプレートの間に配置されたときに実験セットによって実行されました。図2は、サンプルを流れる電流が不可能な実験セットアップのこのような構成により、ポリマーマトリックス内で一貫して整列したGNPのチェーンを取得できることを示しています。

AC電界によるMWCNT / Larit 285複合材料処理の場合、電界チェーンの方向への伸びの形成も観察されました。 AC電界にさらされる時間が長くなると、別個のチェーンが太くなります。しかし、MWCNT /エポキシ複合材料での整列した鎖形成の特徴的な時間は数分ですが、GNP /エポキシ複合材料では埋め込み電極構成では数秒です。さらに、GNPの形状とサイズにより、GNP /エポキシ複合材料の整列したフィラー分布は、MWCNT /エポキシ複合材料よりも小さいAC電界の大きさで形成できます。しかし一方で、MWCNTと比較してその形状とサイズのためにGNPの移動性のために、GNPフィラーとのバルク複合材料の形成は複雑です。複合材料が完全に重合していない場合、GNPの整列したネットワークは、電界をオフにした直後に破壊される傾向があります。

GNPs /-およびMWCNTs /エポキシ複合材料のAC電界形成下での整列ネットワークのすべての光学画像を考慮すると、カーボンフィラーのタイプのみを変更した場合の同じ条件下で、整列ネットワークはGNPs /エポキシでより速く形成されると結論付けることができます。複合。 MWCNTの場合、凝集する傾向があるため、印加された電界の方向への効果的な整列が妨げられます。 DCフィールドは、複合材料で整列したネットワークを形成するのに効果的ではないことに注意してください[26]。

異なる形態のフィラーの電場支援配向の光学顕微鏡特性による観察を説明するために、AC電場作用下でのエポキシマトリックス中のカーボンナノ粒子回転の特徴的な時間を理論的に推定した。

粘性媒体における炭素粒子の整列のモデリング

フィラー形成法の特定の空間分布を備えた複合材料のメカニズムは、誘電体マトリックスに埋め込まれたすべてのカーボンナノ粒子が、ポリマーと粒子の間の界面の分極により、AC電界作用下で分極を受けることです。一般に、分極モーメントと電場ベクトルは、ナノ粒子の異方性のために非線形です。したがって、電場が活性化されると、電場の方向にカーボンナノ粒子を回転させるトルクが発生します。この場合の粒子の回転運動は次の方程式で表されることが知られています[16]：

ここで私 カーボンナノ粒子の慣性モーメントです。 Θ 粒子と電界方向の間の角度です。 T _η 減衰トルクです。 \（{T} _ {\ mathrm {align}} \ approx \ left [\ overrightarrow {\ mu} \ times \ overrightarrow {E} \ right] \）はフィールドに起因するトルクです。 \（\ overrightarrow {\ mu} =f \ left（\ varepsilon、{\ sigma} _1、{\ sigma} _2、v \ right）\）は、誘電率（）の値に依存する分極モーメントです。 ε ）および導電率（σ ₁ 、σ ₂ ）ナノ粒子とマトリックスの; v = f （ m 、 l 、 d ）は、その重量（ m ）に依存するカーボンナノ粒子の体積です。 ）および寸法（ l 、 d 。

一般に、分極モーメント\（\ overrightarrow {\ mu} \）は、外部場\（\ overrightarrow {E} \）と粒子の体積νに比例します。 式[28]によって決定されます：

ここで、ε ₀ は自由空間の誘電率、ε _m はマトリックスの誘電率βです。 は無次元パラメータであり、特に包含の形状に依存します。 [28]では、βの式 理想的な導電性ディスクとシリンダーの場合：

これらの依存関係から、\（{\ overrightarrow {\ mu}} _ {II} \ ne {\ overrightarrow {\ mu}} _ {\ perp} \）（ II 粒子の長軸と場の方向の共方向を意味します、⊥-垂直）。したがって、GNPとMWCNTの場合、形状と特性のために\（{\ overrightarrow {\ mu}} _ {II}> {\ overrightarrow {\ mu}} _ {\ perp} \）。

電場作用下での炭素粒子の回転の特徴的な時間と、電場の方向によるその整列を評価するには、式（1）を使用します。 （1）初期条件Θ （ t =0）=Θ ₀ 、\（\ frac {d \ varTheta} {dt} \ left（t =0 \ right）=0 \）が解決されました。 [16]によると、主な運動方程式の項は次のとおりです。

ここで、\（{\ alpha} ^ {\ ast} =\ left（{\ left（{\ varepsilon} _p ^ {\ ast}-{\ varepsilon} _m ^ {\ ast} \ right）} ^ 2 \ right） / \ left（\ left [{\ varepsilon} _m ^ {\ ast} + \ left（{\ varepsilon} _p ^ {\ ast}-{\ varepsilon} _m ^ {\ ast} \ right）{L} _x \ right] \ left（{\ varepsilon} _p ^ {\ ast} + {\ varepsilon} _m ^ {\ ast} \ right）\ right）\）は分極率、\（{\ varepsilon} _ {m、p} ^ {\ ast} ={\ varepsilon} _ {m、p} -j \ frac {\ sigma_ {m、p}} {\ omega} \）、およびε _{m 、 p} 、σ _{m 、 p} は、媒体と粒子の誘電率と導電率、ωです。 =2 πf 、 f -電界周波数。

カーボンナノチューブとグラファイトナノプレートレットの偏光解消係数を決定するには、それらを特定の形状の粒子と見なす必要があります（図5）。 MWCNTは、楕円体としてのみ見なすことができます。楕円体近似におけるMWCNTの楕円率は、\（e =\ sqrt {1-{\ left（2 {r} _0 / l \ right）} ^ 2} \）です。 GNPは、回転楕円体または楕円体と見なすことができます。楕円体近似でのGNPの楕円率は\（e =\ sqrt {1-{\ left（h / 2R \ right）} ^ 2} \）であり、回転楕円体近似では\（e =\ left（2R / h \ right）\ sqrt {1-{\ left（h / 2R \ right）} ^ 2} \）。次に、脱分極係数の式は次の形式になります[28]。

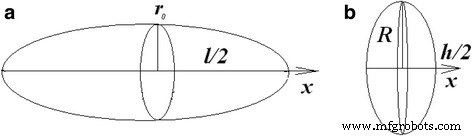
カーボンナノチューブの概略画像（ a ）およびグラファイトナノプレートレット（ b ）

楕円体の場合：

回転楕円体の場合：

上記の式では、 L _x x に沿って外部電界が印加された場合の偏光解消係数です。 -軸（図5のように）、 L _R 外部電界がGNPの半径に沿って印加された場合の偏光解消係数です。

偏光解消係数を直列に使用すると、上記の式は次の形式になります。

楕円体MWCNTの場合：

楕円体GNPの場合：

球状GNPの場合：

さらに、粒子形態の特性を強調するために、CNTの体積を中空円柱の体積として求めました\（\ nu =\ pi l \ left（{r} _0 ^ 2- {r} _i ^ 2 \ right）\ ）、GNPボリュームはディスクのボリュームとして尋ねられましたν =πR ² h 。

カーボンナノチューブの慣性モーメントは、\（I =\ frac {ml ^ 2} {12} \）—長さが l の真っ直ぐな細い棒の慣性モーメントと見なされました。 と m の質量 、回転軸はロッドに垂直であり、その重心を通過します。グラファイトナノプレートレットの慣性モーメントは、\（I =\ frac {mR ^ 2} {2} \）-ディスクの慣性モーメントであり、その半径は R です。 、および m の質量 、ディスクはその平面軸に垂直な方向を中心に回転しています。

次に、前述のすべてのアプローチを使用し、数値パラメータを設定して、AC電界処理の時間に伴う電界方向に対する異なる形態の粒子の傾斜角の変化の計算を実行しました。

紙[29]に基づいて、微細なグラファイトとカーボンナノチューブを含む複合材料の誘電率の実数部と複素数部の実験的な濃度依存性がニールセンの公式と方程式で記述されました。

GNP εの計算では、 _{p （ GNP ）} =34.3、MWCNTの場合、ε _{p （ CNT ）} =62.2が取得されました。

粒子の幾何学的パラメーターは表1から取得されました。他の使用された数値パラメーターに関しては、ε ₀ =8.85×10 ⁻¹² F / m、η =0.75 Pa×s、 f =15 kHz、ε _m =2.8 ε ₀ [30]、σ _m =10 ^-6 Sm / m [16]。個々の炭素粒子の導電率をσとしました。 _{p （ CNT ）} =10 ⁵ Sm / m [31]、σ _{p （ GNP ）} =10 ⁵ Sm / m [32、33] _。

図6は、 L の場合の、電界作用時間の印加電界依存性の方向に対する粒子の傾斜角を示しています。 _x 式によって評価されました。 （2）と（3）。結果は、電界強度の2つの値で見つかりました。1kV/ m（図6а）と36 kV / m（図6b）で、粒子が最初にほぼ完全に無秩序であると仮定しています（Θ> （ t =0）=π /2.05）。

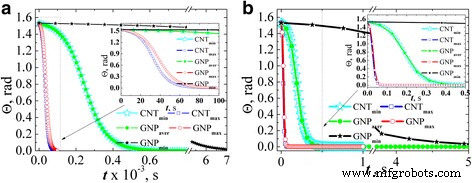
AC電界強度1kV / m（ a ）の楕円近似で推定された電界方向に対するカーボンフィラー粒子の傾斜角の変化 ）および36 kV / m（ b ）

粒子のアスペクト比と電界による整列時間の間には明確な相関関係があります。つまり、整列の最大時間は、アスペクト比が最も低い粒子（GNP _min ）の場合です。 ）。 GNP _max の場合 およびCNT _max 、アラインメント時間はほぼ等しく、アラインメントの等しい時間はGNP _aver の場合です。 およびCNT _min 。

図7は、式（1）によって推定された偏光解消係数の値を示しています。 （2）および（3）GNPおよびMWCNTの場合。 L _x は幾何学的要因であり、シミュレートされた楕円体の半軸の絶対値ではなく、それらの比率に依存します。したがって、 L _x は粒子のアスペクト比の直接関数です。

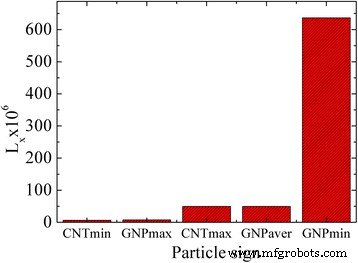
式によって評価されたGNPおよびMWCNTの偏光解消係数。 （2）と（3）

つまり、偏光解消係数が問題の主なパラメータです。その発現は粒子の形態とサイズに依存するため、GNPとMWCNTの回転の特徴的な時間は異なります。

図8の内容は、 L の場合の、印加電界の方向に対するGNPの傾斜角の電界作用時間への依存性を示しています。 _R 式によって評価されました。 （5）。結果は、電界強度の2つの値で見つかりました。1kV/ m（図8а）と36 kV / m（図8b）で、粒子が最初にほぼ完全に無秩序であると仮定しています（Θ> （ t =0）=π /2.05）。比較のために、MWCNTの角度依存性の計算結果（ L _x 式によって評価されました。 （2））同じグラフで紹介されています。

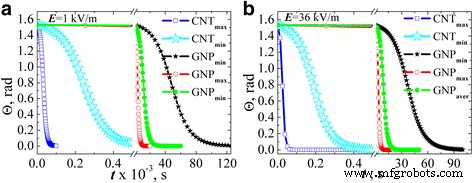
AC電界強度1kV / m（ a ）でのMWCNTの楕円体近似およびGNPの回転楕円体近似で推定された電界方向に対するカーボンフィラー粒子の傾斜角度の変化 ）および36 kV / m（ b ）

図9は、GNPが偏光解消係数を持つ回転楕円体であるという近似で、印加電界の方向に対するGNPの傾斜角の電界作用時間への依存性を示しています（4）。 AC電界強度1kV / m（図9а）および36 kV / m（図9b）について、初期に粒子がほぼ無秩序（Θ）であると仮定して評価を行いました。 （ t =0）=π /2.05）。

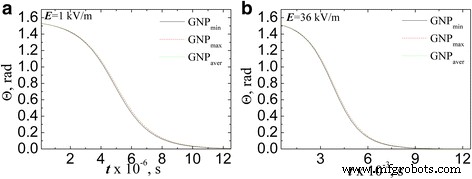
回転楕円体近似（ L ）で推定されたフィールド方向に対するGNPの傾斜角の変化 _x 式によって取られました。 （4））AC電界強度1 kV / m（ a ）および36 kV / m（ b ）

図9のデータに示されている分析から、次の結論が得られました。まず、電界軸が x と同一方向に向けられていると仮定した場合。 -GNPの軸では、回転時間は、フィールド軸とGNP半径の同一方向の場合の計算と比較して大幅に増加します。また、この動作はGNPのアスペクト比とは関係ありません。第二に、依存の過程は、アスペクト比が異なる粒子では最小限に異なり、プロセス時間の特定の時点で、より整列した粒子は、アスペクト比が最小のGNP _min の粒子になります。 一方、GNP _aver およびGNP _max 角度は一致します。この動作は、上記の場合の1に近い脱分極係数の値によるものです。

したがって、推定は、交流電界作用下での炭素粒子の回転時間は、それらの形態およびアスペクト比に依存することを示した。モデルは、複合材料ではポリマーマトリックスに埋め込まれた1つの粒子を考慮していることに注意してください。この場合、初期傾斜角が異なる粒子の集合があります。これが、ネットワーク形成全体の実際の特徴的な時間が推定時間と大きく異なる可能性がある理由の1つです。

その上、個々のチューブが絡み合っている複合混合物でMWCNTのそのような分布を達成することは複雑です。カーボンナノチューブは、その表面の相互作用により絡み合う傾向があることが知られています。したがって、複合混合物のアラインメントにおけるMWCNTのリアルタイムは、理論的に推定されたものよりも大幅に高くなります。その上、MWCNTの同じ含有量の複合混合物の粘度は、GNPとの複合混合物の粘度よりも高い。これらすべての要因により、推定されたように、複合材料中のMWCNTの迅速な整列が妨げられます。

固体複合材料の電気的特性

研究の中で、エポキシマトリックス中に整列し、ランダムなフィラー分布を持つ、調製されたGNP / Larit285複合材料の抵抗率の値が実験的に発見されました。図10は、整列したランダムなフィラー分布を持つGNP / Larit285複合材料の電気伝導率の濃度依存性を示しています。複合材料サンプルの電気的特性は、複合材料製造電界方向に適用された縦方向および垂直方向で調査されました。図11は、MWCNT / Larit 285（а）[27]およびGNP / Larit 285（b）複合材料の導電率の濃度依存性を両対数スケールで示しています。

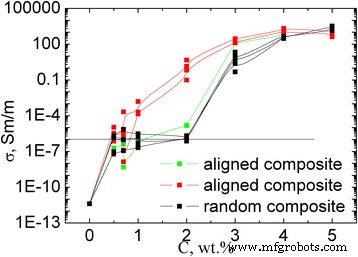
Concentration dependence of electrical conductivity of GNPs/Larit 285 composites with aligned and with random filler distribution in logarithmic scale

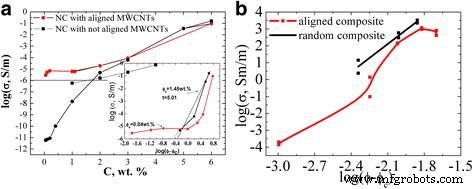
Concentration dependence of conductivity of MWCNTs/Larit 285 (а ) [27] and GNPs/Larit 285 (b ) in log-log scale

The lowest values of the conductivity σ correspond to the samples of epoxy resin without filler (conductivity of 10 ⁻¹¹ Sm/m). With GNPs adding to the composite, its conductivity increases and reaches the value of σ =10 ⁻⁶ Sm/m (this value is considered as percolation level) at GNPs content с in composite of φ _с =2 wt% for the composites with random filler distribution. For the GNPs/Larit 285 composites with aligned filler distribution, percolation concentration is of φ _с =0.84 wt%. Thus, materials of the identical composition are characterized by different values of percolation threshold depending on the method of preparation and filler distribution in the polymer matrix (aligned or random).

Conductivity of GNPs/Larit 285 composites smoothly increases with the increment of GNPs content for both types of the samples while the shape of the dependence is completely different for the MWCNTs/Larit 285 composites obtained by the same method [27] (see Fig. 11). Concentration dependence of conductivity of MWCNTs/Larit 285 composites increases with the increment of MWCNTs content at low filler content until it reaches a plateau, then conductivity increases again. Such a difference of conductivity concentration dependence can be explained by another process of conductive network formation if the fillers are of different morphology. MWCNTs/epoxy composites are characterized by crossed framework structure formation while in GNPs/epoxy composites chained structure appears. GNPs addition to the polymer matrix smoothly increases the number of conductive links in composite. In case of entangled by themselves frame MWCNTs, there is an area where nanotubes addition to the matrix has little effect on its conductivity.

Statistical percolation model operates with probabilities of particles in composite to create a conductive chain at their certain content. As it was shown in our paper, manufactured with electric field treatment, composites become conductive at lower content of carbon filler due to activation of dynamic percolation which is a phenomenon when conductive chain formation is stimulated by external influences at such a content of conductive particles in composite which is not enough for statistical percolation.

It should be noted that the existence of two types of percolation transitions is a characteristic feature of composite materials which are in low-viscosity state during the manufacture [34]. The higher value of percolation concentration cannot be changed by varying the manufacturing conditions of the composite since it is defined by statistical percolation theory. Statistical percolation threshold is defined by the filler type, its aspect ratio, surface state of polymer and filler, wettability, uniformity of filler distribution, and its content in polymer matrix. As we have shown, dynamical percolation threshold can be shifted by activating of filler particle movement in polymer matrix, by electric field action, and, thus, promoting a conductive network formation. The value of dynamic percolation threshold can be changed with method of composite manufacture change. We have established that in case of filler alignment under electric field action, dynamical percolation threshold is defined not only by the above parameters but also by parameters of the applied field and polymer matrix viscosity, filler morphology.

Conclusions

1. 1.

   Nanocarbon-polymer composite material with aligned distribution of graphite nanoparticles in epoxy matrix has been produced by exposing to a high-voltage AC electric field. The influence of electric field treatment time, strength, and configuration of electric field on formation of aligned GNPs network in liquid polymer medium was investigated by optical microscopy.

2. 2.

   It was shown that the influence of AC electric field at composite fabrication process leads to the manifestation of two types of percolation transitions:statistical and dynamic ones. In addition, the aspect ratio of the filler particles and the character of the formation of the conducting cluster, depending on the shape of the particles, determine the shape of the σ =f(c) dependence and the critical concentration of both dynamic and statistical percolation thresholds.

3. 3.

   The effects of the morphology of the filler particles on the process of nanocarbon alignment in polymer matrix under AC electric field have been investigated by estimating of carbon nanotube and graphite nanoplatelet rotation time using an analytical model based on effective medium approach. The theoretical evaluation of characteristic time of carbon nanoparticle of different morphology rotation under AC electric field action have shown that rotation time of carbon nanoparticle is determined by its depolarization factor which in turn depends directly on the aspect ratio of particle.

4. 4.

   The investigation of concentration dependences of conductivity of composites GNPs/Larit 285 with aligned by AC electric field action filler distribution and random filler distribution in epoxy matrix have shown that under AC electric field action composites, percolation threshold decreases essentially from ϕ _c =2 wt% for composites with random filler distribution of GNPs to ϕ _c =0.84 wt% for the obtained under AC electric field action GNPs/Larit 285 composites.

略語

AC:

Alternative current

AFM:

Atomic force microscopy

CNTs:

Carbon nanotubes

DC:

Direct current

GNPs:

Graphite nanoplatelets

MWCNTs:

Multiwall carbon nanotubes

SEM：

走査型電子顕微鏡