劣化特性の数値解析によるメタ表面偏光子の高性能の向上

背景

ナノスケールでの光の制御は、ナノ光学およびナノフォトニクスで広く研究されてきました。その結果、これまでにさまざまなタイプのフォトニックナノ構造が提案されてきました。たとえば、超高品質（Q）ファクターのフォトニック結晶（PhC）ナノキャビティ[1]は、光をサブ波長領域に閉じ込めることができます。 PhCキャビティと同様に、高いQファクターは、マイクロディスク[2、3]、球状[4]、およびトロイダル[5]キャビティによって実現されます。 Qファクターが高いキャビティは、通常、透明な誘電体材料で構成されています。これらの誘電体キャビティとは対照的に、金属キャビティはQ値が低くなりますが、キャビティ全体のサイズを小さくすることができます。特に、プラズモンサブ波長キャビティは、非常に小さなスケールで光を制御するために重要です[6]。プラズモン空洞はQ値が低いですが、光を深いサブ波長領域に押し込むことができます[7]。この非常に閉じ込められた光は、フォトニクスとエレクトロニクスを融合するための鍵になると期待されています[8]。

上記のフォトニックナノ構造に加えて、メタ表面は、高機能で超薄型の光学デバイスを設計するために最近かなりの注目を集めています。屈折[9]、反射[10]、フォトルミネッセンス[11]、蛍光[12–14]、波長板[15]、およびビームスプリッター[16]を制御するさまざまなタイプのメタサーフェスがあります。偏光状態は、メタサーフェスによって制御できる光の基本的かつ重要な特性の1つです[17–22]。数値的および実験的研究により、積み重ねられた相補構造を備えたメタ表面偏光子は、近赤外領域で10,000のオーダーの高い消光比を持っていることが示されています[23–26]。バビネの原理により、相補構造はほぼ同じ波長で共振します[27、28]。相補構造が特定の偏光に対して高い透過率を示す共鳴上にある場合、他の構造は同じ偏光に対して低い反射率を示す共鳴外です。その結果、構造全体が高い透過率を示します。直交分極の場合、電界と磁界の役割が交換され、高い反射率が得られます。したがって、相補的な構造を持つメタ表面は、高い消光比を示します。しかし、メタ表面は大気中で劣化する銀で構成されているため、この高性能の安定性と信頼性には深い懸念があります。この問題を回避するための代替アプローチは、プラズモン材料として金を使用することですが、これは金属損失の増加により偏光子の性能を低下させます。したがって、実際のアプリケーションでは、メタ表面偏光子の安定性と信頼性に対処する必要があります。

本研究では、メタ表面偏光子の劣化特性を調査します。偏光子の消光比が時間劣化を示すことを示します。劣化の原因として、偏光子の高性能に対する表面形態の影響に焦点を当てています。形態を説明するために、2つのモデルを紹介します。 1つは、ガウスホワイトノイズを伴う周期曲線によって表面粗さを記述し、もう1つは、ランダムに分布したナノ粒子を使用して粗さを記述します。また、金属損失が高性能に与える影響についても調査しました。これらの数値計算を通じて、劣化の原因となる重要な要因を明らかにし、高い消光比を備えた最適化されたメタ表面偏光子を提案します。

メソッド/実験

高消光比測定の実験装置を図1に模式的に示します。光として周波数3倍のNd：YAG（イットリウム鉄ガーネット）レーザー（Optolette 355、Opotek）で励起された光パラメトリック発振器（OPO）を使用しました。ソース。パルス幅と繰り返し率はそれぞれ7nsと20Hzでした。 OPOからのアイドラー光は、レンズによってサンプルに焦点を合わせ、グランレーザープリズム（GLP）によって直線偏光されました。透過したアイドラー光は、拡張InGaAs光検出器（Edmund Optics）によって測定されました。この光学システムでは、単一パルスからの光強度の変動により、信号対雑音（S / N）比が低下します。したがって、この変動の影響を取り除くために、単一パルスの平均透過率を測定しました。単一パルスの光強度を監視するために、レンズとGLPの間に1対のビームサンプラーを挿入しました。アイドラー光の一部は、2番目のビームサンプラー（BS2）で反射された後、反射減光（ND）フィルターで再び反射され、光検出器に損傷を与えないように反射レーザー強度が調整されました。調整されたレーザーは、ピンホールを介して拡張InGaAs光検出器（Edmund Optics）に入射し、BS2の背面で反射された不要な「ゴースト」光を遮断しました（図1の挿入図を参照）。最初のビームサンプラーは、光路の偏差の補償器として機能します。

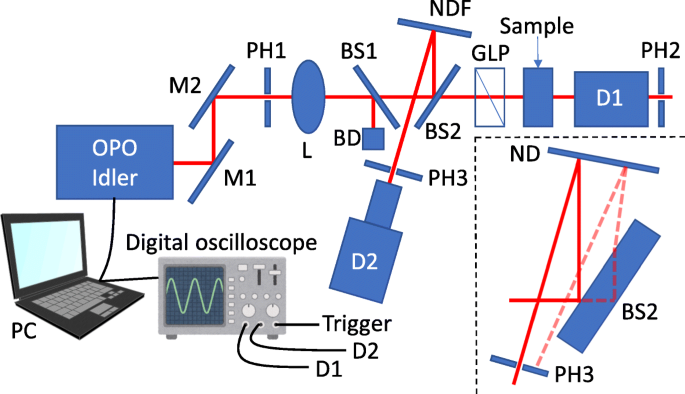
消光比測定の実験装置の概略図。 Mミラー、PHピンホール、Lレンズ、BSビームサンプラー、BDビームダンパー、NDFニュートラルデンシティフィルター、GLPグランレーザープリズム、D検出器

この設定を使用して、次のように消光比を評価しました。送信信号は D と計算されます ₁ =（1- R _BS2 ） T _GLP T _サンプル 私 、ここで R _BS2 、 T _GLP 、 T _サンプル 、および I BS2の反射率、GLPの透過率、サンプルの透過率、およびBS2の前の光強度です。検出器2の信号強度は D と計算されます。 ₂ = R _BS2 R _NDF 私 、ここで R _NDF は反射NDフィルターの反射率です。検出された信号が光強度に比例するように、光強度が十分に減少することに注意してください。 D の使用 ₁ および D ₂ 、 T を計算できます _サンプル として

T を評価するには _サンプル 、ビームサンプラーなどの光学素子の反射率と透過率も測定する必要があります。消光比、つまり透過率に焦点を当てているので、これは不要です。サンプルを90°回転させ、同じ設定で透過率を測定することにより、簡単に消光比ηを得ることができます。 として

ここで、上付き文字のHとLは、それぞれ高い透過率と低い透過率を示す偏光状態を示します。この論文では、比率 D を測定しました ₁ / D ₂ 直交偏光状態について、消光比ηを評価しました 。

測定データの妥当性を確認するために、散乱行列法[29、30]と逆フーリエ法[31]を組み込んだ厳密な結合波解析（RCWA）に基づいて数値計算を行いました。 Agとシリカの誘電率はそれぞれ[32]と[33]から得られました。計算に使用した逆格子ベクトルの数は2601でした。

粗い金属構造の透過率を計算するために、有限要素法に基づくCOMSOLMultiphysicsの商用ソフトウェアを使用しました。以前の研究[34]では、光学応答に対する粗さの影響は、金属の誘電率の虚数部の増加によって説明されていました。この論文では、金属損失の増加に加えて、透過率に対する粗さによる構造変化の直接的な影響も考慮しました。これら2つの効果を別々に扱いました。構造変化の影響のみを考慮する場合、粗さのある金属構造にバルク誘電率を適用しました。一方、損失の増加の影響のみを考慮する場合、粗さのない金属構造に修正誘電率を適用しました。数値計算の相対公差を1％未満に設定しました。

結果と考察

図2aは、3層のメタ表面偏光子の概略図を示しています。第1層は第3層と相補的な構造を持ち（図2bを参照）、両方の層が銀（Ag）を含みます。第2層と基板はシリカ（SiO ₂ ）。図1cに示すように、メタサーフェスには長方形の穴（150nm×540nm）のペアの配列があり、 x の周期は900nmです。 および y 方向。金属層と誘電体層の厚さは、それぞれ45nmと200nmです（図2dを参照）。サンプルは、その後のドライエッチング技術と組み合わせたナノインプリントリソグラフィーによって準備されました[35]。サンプル準備の詳細は[26]に記載されています。図3は、準備されたサンプルの走査型電子顕微鏡（SEM）画像を示しています。

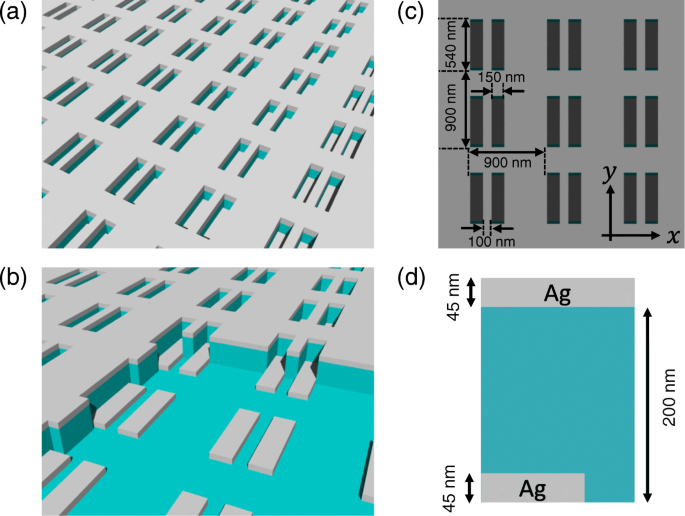
メタ表面偏光子の概略図（ a ）3つの層（ b ）。メタサーフェスには、 x に900nmの周期を持つ長方形の穴のペアの配列があります。 および y 方向（ c ）。金属層と誘電体層の厚さは、それぞれ45nmと200nmです（ d ）

a のSEM画像 メタ表面偏光子と b その拡大画像

x のサンプルの透過率を測定するために、分光光度計（V-7200、日本分光、日本）を使用しました。 および y 分極。図4に測定結果を示します。青と緑の線は、 x の透過率を示しています および y それぞれ分極。高透過率に対応する青い線は、高いS / N比で測定されます。ただし、透過率が低いことに対応する緑色の線は、S / N比が低く、偏光子の消光比が高いことを示しています。特に、緑色の線は、透過光の強度が分光光度計のノイズレベルを下回っているため、1350nmより長い波長で負の信号を示します。そのため、前のセクションで説明した光学システムを使用して、高い消光比を測定しました。

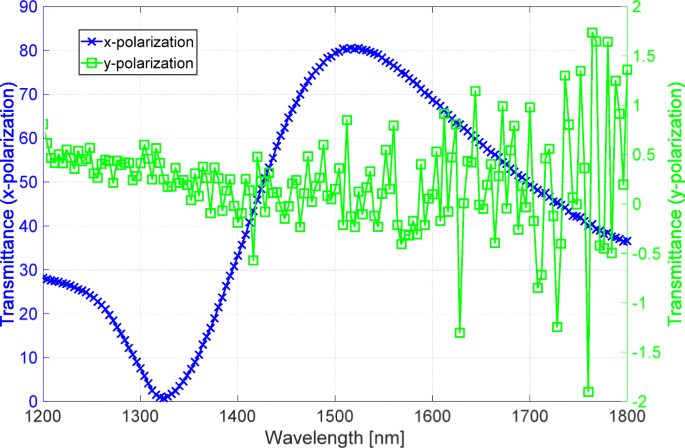
分光光度計によって測定された透過率スペクトル。青と緑の線は x のスペクトルです および y それぞれ分極

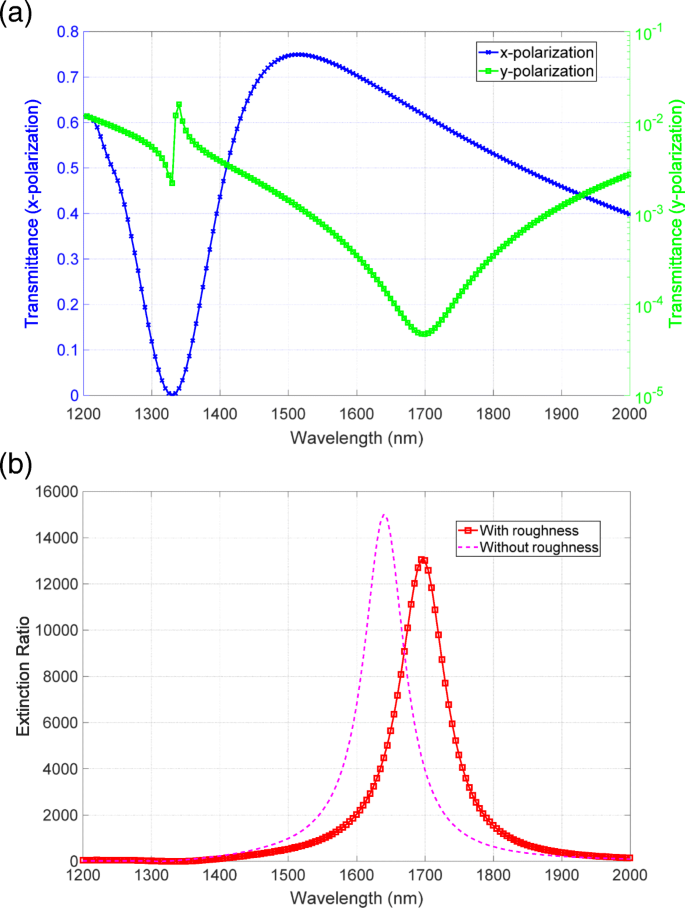
図5aは、 x で測定された透過率スペクトルを示しています。 および y 分極。高透過率に対応する青い線は、分光光度計で測定された透過率と同様のスペクトルプロファイルを持っています。低透過率に対応する緑色の線は、分光光度計では測定されなかった、1625nmの波長の周りに明確な落ち込みがあります。 x の透過率を除算する y の分極 偏光については、図5bに示す消光比スペクトルを評価しました。消光比スペクトルのピーク値は、1640nmの波長付近で20,000を超えています。

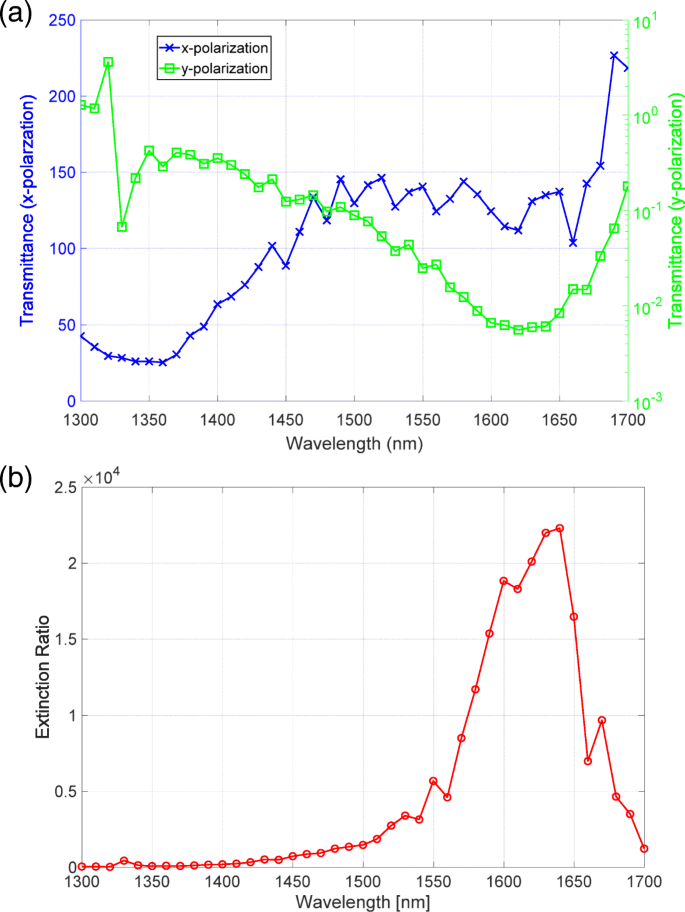
a x の透過率スペクトル （青）と y （緑）図1に示す設定で測定された偏光。 b メタ表面偏光子の消光比スペクトル

測定データの妥当性を検討するために、測定スペクトルを数値計算結果と比較しました。図6aに示すように、高透過率スペクトルは、分光光度計で測定されたスペクトルと一致していました。対数目盛で表示される低透過率スペクトルは、1640nmの波長の周りに明確な落ち込みがあります。この特徴は、観測されたスペクトルの特徴とよく一致しました。図6bに示す消光比スペクトルのピークは15,000であり、観測値に近い値です。このように、測定された透過率と消光比のスペクトルは数値計算の結果と一致しており、20,000を超える高い消光比を観測することに成功したことを示しています。

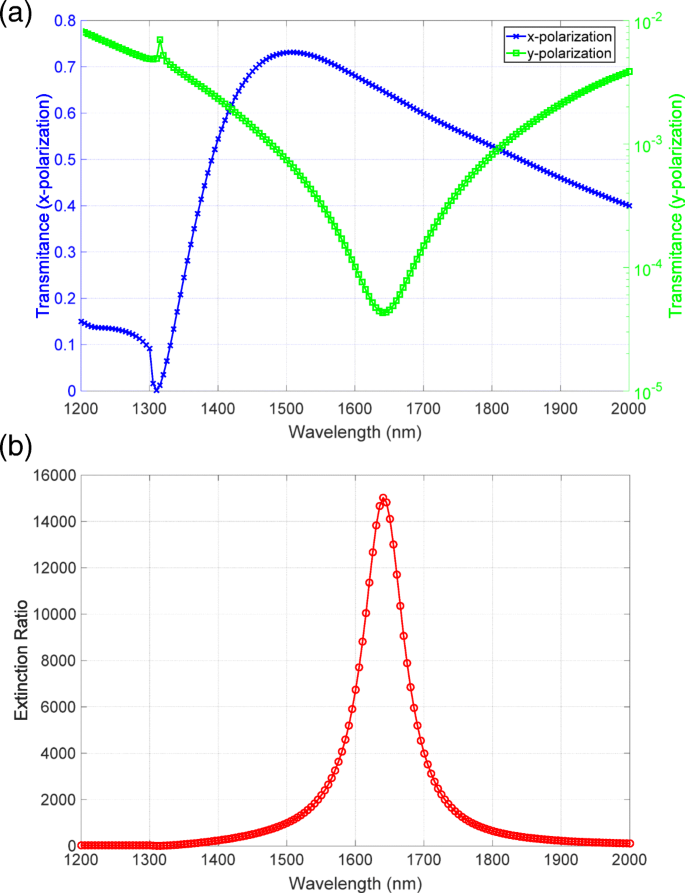
a の数値計算結果 透過率と b 消光比スペクトル。 a の青と緑の線 x に対応 および y それぞれ分極

高い消光比を持つメタ表面の実験的実証に続いて、メタ表面は大気中で劣化しやすいAgを含むため、時間劣化に対する安定性に焦点を当てます。図7は、消光比の時間劣化を示しています。赤、緑、青の線は、それぞれ金属蒸着後6、7、9日後に観測された消光比スペクトルです。赤い線のピーク値は20,000を超えています。赤線測定の1日後、消光比は低下しましたが、ピーク値は10,000を超えていました。しかし、緑色の線を測定してから2日後、消光比は大幅に低下し、ピーク値は500になりました。青色の線は線幅が広く、損失の増加がこの低下に関与していることを示しています。したがって、消光比は大幅に低下し、性能は1桁低下しました。また、分解後の消光比スペクトルの赤方偏移ピークも見つかりました。パフォーマンスの低下を伴う重要な要因の研究について説明します。

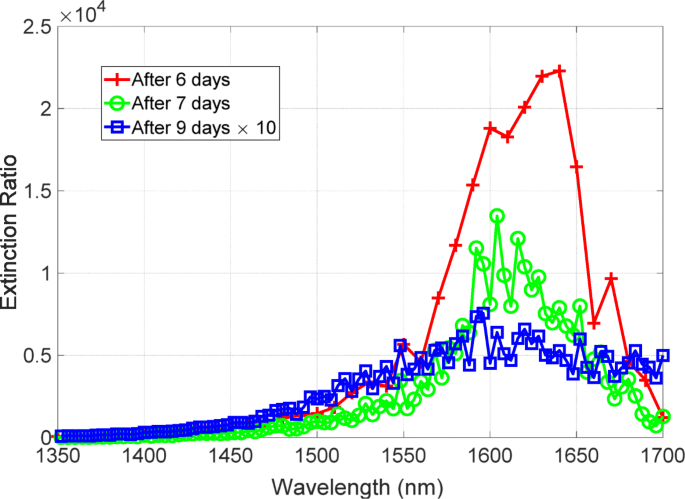
消光比の時間劣化。赤、緑、青の線は、金属蒸着後6、7、9日間の消光比スペクトルです

分解は急速に進行し、吸光スペクトルの線幅が広がり、この分解プロセスにいくつかの構造変化が関与していることを示しています。したがって、金属ナノ構造の表面形態が偏光子の性能に影響を与える方法を調査します。形態を説明するために、2つのモデルを紹介します。 1つはガウスホワイトノイズを伴う周期曲線で表面を表し、もう1つはランダムに分布したナノ粒子で表面を表します。

まず、周期曲線を使用してモデルを調査します。図8aは、モデル化されたサーフェスを示しています。 CPU時間とメモリリソースを節約するために、下部の金属層にのみ粗さを導入しました。表面が粗いため、金属層の有効厚さは異なります。したがって、図8bの緑色の矢印で示されている最下層の厚さを変更しました。図9a、bは、それぞれこの構造の透過率と消光比のスペクトルを示しています。粗さが存在する場合でも、メタ表面偏光子は10,000のオーダーの高い消光比を持ち、粗さが性能を大幅に低下させないことを示しています。数値計算はまた、厚さの減少に伴う消光比の赤方偏移スペクトルを示しています。この赤方偏移は、図9aに示す透過率のスペクトル特性によって解明されます。高透過率は金属の厚さの変化に対して感度が非常に低く、低透過率は厚さが薄くなるにつれて赤方偏移したディップ位置になります。消光比のピーク位置は、低透過率のディップに依存し、赤方偏移を引き起こします。計算に現れた赤方偏移は、実験的に観察された赤方偏移の特徴と一致していません。

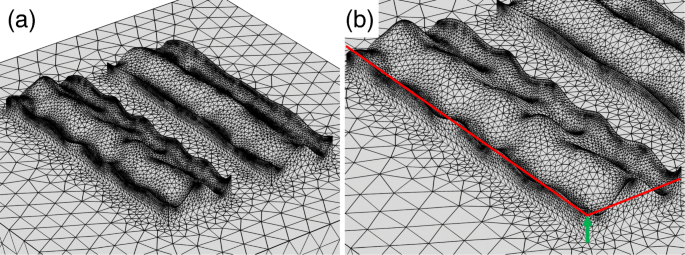
a ガウスホワイトノイズのある周期曲線を使用してモデル化された粗面。 b 緑の矢印で示されるベースの厚さは、計算で変化します

a 透過率と b 図8に示す最初のモデルの消光比スペクトル。下部の金属層のベースの厚さは、5nmのステップで40から55nmまで変化します。

次に、ナノ粒子によるモデルの調査を行います。図10aは、モデル化された表面を示しています。図10bに示すように、半径15、20、および25nmのナノ粒子が下部の金属構造の表面にランダムに分布しています。均一に分布した乱数に従って、半球形のナノ粒子を表面に配置しました。ランダムな分布では、一部のパーティクルはわずかに空間的にオーバーラップし、パーティクル間のメッシュサイズは非常にメモリを消費します。この場合、メモリを節約するために、パーティクルの1つを手動でシフトし、メッシュサイズを小さくしました。下部構造の厚さを40nmに設定しました。図11a、bは、それぞれこの構造の透過率と消光比のスペクトルを示しています。最初のモデルと同様に、消光比スペクトルのピーク値は10,000のオーダーであり、大幅に低下することはありません。赤方偏移したピークは、ナノ粒子の存在下でも現れています。これらの特徴も最初のモデルで観察されたものと同じですが、劣化特性と青方偏移の実験結果と一致していません。

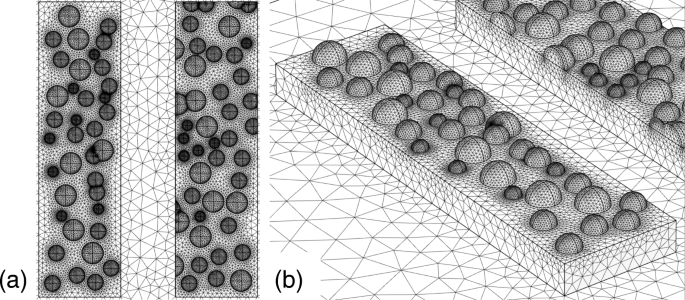
a 上面図と b ランダムに分布したナノ粒子を使用してモデル化された粗い表面の鳥瞰図

a 透過率と b 図10に示す2番目のモデルの減光スペクトル

この段階で、表面形態の変化がメタ表面偏光子の性能を大幅に低下させないことを数値的に示しました。形態のこの堅牢性は、バビネの原理に起因しています。バビネの原理は、表面の形態には言及していませんが、補完的な構造のスクリーンに言及しています。この原理に基づく高性能偏光子は、表面粗さが存在する場合でもスクリーンが不変であり、形態に対する堅牢性をもたらすため、形態の影響を強く受けません。したがって、劣化の原因として、表面形態の別の影響を考慮する必要があります。ここでは、形態に関連する金属損失に焦点を当てます。表面粗さが増加すると、表面散乱と粒界効果により、Agの虚数部が増加します[36、37]。この損失の増加は、γとして記述されるドルーデモデルの減衰定数によって説明されます。 =ρ n e ² / m _e 、ここでρ 、 n 、 e 、および m _e それぞれ、電気抵抗率、電子密度、電子電荷、および有効電子質量です。抵抗率は2つの項で構成されます。 1つはバルク抵抗率で、もう1つは表面抵抗率です。表面抵抗率ρ _s 横方向の相関長ξに反比例します つまり、ρ _s ∝ ξ ^-1 [38]。粗さの増加に伴い、横方向の相関長ξ 減少するため、表面抵抗率と金属損失が高くなります。この物理的メカニズムは、周期境界条件が使用され、大まかな周期構造が想定されているため、計算には含まれていません。この金属損失の増加が消光比に与える影響を考慮し、Agの誘電率を次のように変更します。

ここで、ε _Ag [32]、 C から得られるAgの誘電率です。 は金属損失の増加を表す定数であり、iは虚数単位を示します。実数部と虚数部はクラマース・クローニッヒの関係によって接続されているため、誘電率の実数部は虚数部の増加に続いて変更する必要があることに注意してください。この研究では、定性的な議論を行うために虚数部のみを変更しました。この修正された誘電率を使用して、消光比スペクトルを計算します。この結果を図12に示します。ここで、定数 C は1から5まで変化します。金属損失の増加に伴い、消光比は大幅に減少します。さらに、スペクトルのピーク位置は、損失の増加に伴って赤方偏移の特徴を示しました。劇的な劣化と青方偏移のこれらの特徴は、実験的に観察された特徴とよく一致しています。この青方偏移の起源は次のように解明されています。低透過率のディップ値は、金属損失の増加とともにますます浅くなります。その結果、高透過率のピーク値から消光比への寄与が大きくなります。ピーク位置は金属損失に対して強い感度がなく、ディップ位置よりも波長が短いため、消光スペクトルの青方偏移が発生します。したがって、虚数部の増加が劣化の原因となる重要な要因であることがわかりました。

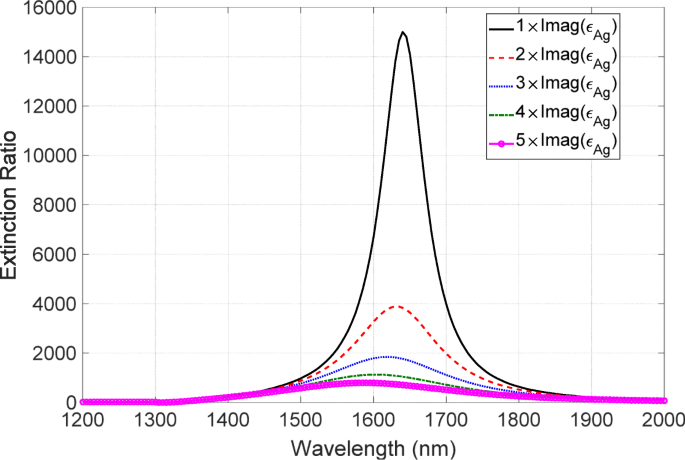
吸光スペクトルの金属損失依存性。黒、赤、青、緑、マゼンタの線は、 C の場合に対応しています。 それぞれ=1、2、3、4、5

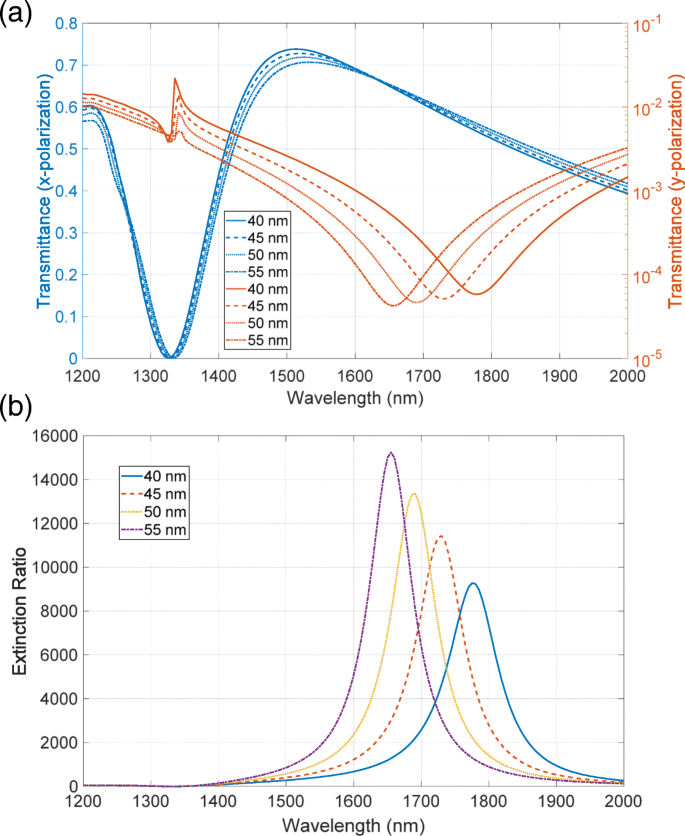
相補的な金属層の厚さを変えることにより、消光比を高めることを提案します。高透過率のピーク位置は、低透過率のディップ位置よりも短い波長にあります。消光比を高めるには、これらのピーク位置とディップ位置を互いに近づける必要があります。バビネの原理によれば、ピークとディップは同じ波長でなければなりません。ただし、原理は、相補構造が無限に薄い厚さの完全電気導体で構成されていることを前提としています。これは、近似下でも光学領域で検証するのが困難です。結果として、相補構造は異なる共鳴波長を持ちます。波長を調整するために、共振の原因となる固有モードの特性を考慮します。図13a、bは、それぞれ図6に示した透過率のピーク位置とディップ位置での電界と磁界の分布パターンを示しています。これらのフィールド分布は、 z に示されています。 − x y の平面 入射光強度1Wで=0。高透過率の固有モードは上部の金属構造に電気双極子の特性があり、低透過率の固有モードは下部構造に磁気ループの特性があります。高透過率の共振波長は、 z の空気穴の幅によって決まります。 − x 飛行機。これは固定パラメータであり、調整することはできません。一方、低透過率の共振波長は、 z の下部構造の断面積によって決まります。 − x 飛行機。これは、金属の厚さを変えることによって調整可能です。これらの調整は、透過率の厚さ依存性と一致しており、高透過率のピーク位置は下部金属層の厚さに対する感度が低く、低透過率のディップ位置は高感度です。この分析に基づいて、次のように波長を調整します。厚みが増すと断面積が大きくなり、低透過率の共振波長が短波長にシフトします。その結果、ピーク位置とディップ位置が近くなり、消光比が向上します。これを確認するために、透過率と消光比のスペクトルの厚さへの依存性を計算します。この計算では、上部の金属層の厚さを45nmに固定しました。図14aは、 x の透過率スペクトルを示しています。 および y 分極。厚みが増すと、低透過率の伏角位置が短波長にシフトし、伏角が深くなります。一方、高透過率のピーク位置は、ピーク値が約5％減少しても、厚みを変えても大きな影響を受けません。図14bは、消光比のスペクトルを示しています。厚さが35または40nmの場合、低透過率のディップは45 nmのディップよりも浅くなり、消光比が低くなります。厚さが50または55nmの場合、ほとんど強調されません。これは、高透過率のピーク値の低下により、ピーク位置とディップ位置の調整による向上が相殺されるためです。厚さが60または65nmの場合、消光比が明らかに向上します。これは、より深いディップ値と位置調整による強化の組み合わせによるものです。数値的に示したように、相補的な金属構造の厚さを調整することにより、消光比のさらなる向上を実現することができます。このようなさまざまな厚さは、金属蒸着を繰り返すことによって実現できます。まず、 a の厚さの金属蒸着 パターン化された基板上で実行されます。次に、きれいな布で拭くことにより、金属の厚さが a の基板の表面から最上部の金属層のみが除去されます。 。続いて、 b の厚さの金属堆積 サンプルに対して実施されます。その結果、上層と下層の厚さは b になります。 および a + b それぞれ。

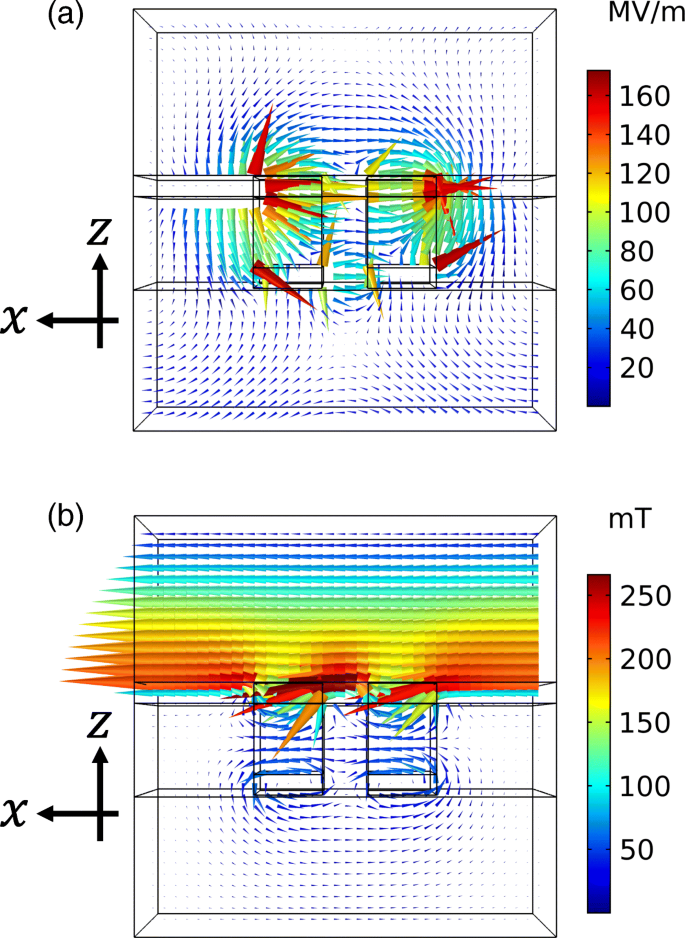
a 図6に示す高透過率のピークでの電界分布パターン。 b 図6に示す低透過率のディップでの磁場分布パターン。疑似カラーはベクトル場の強度を示します

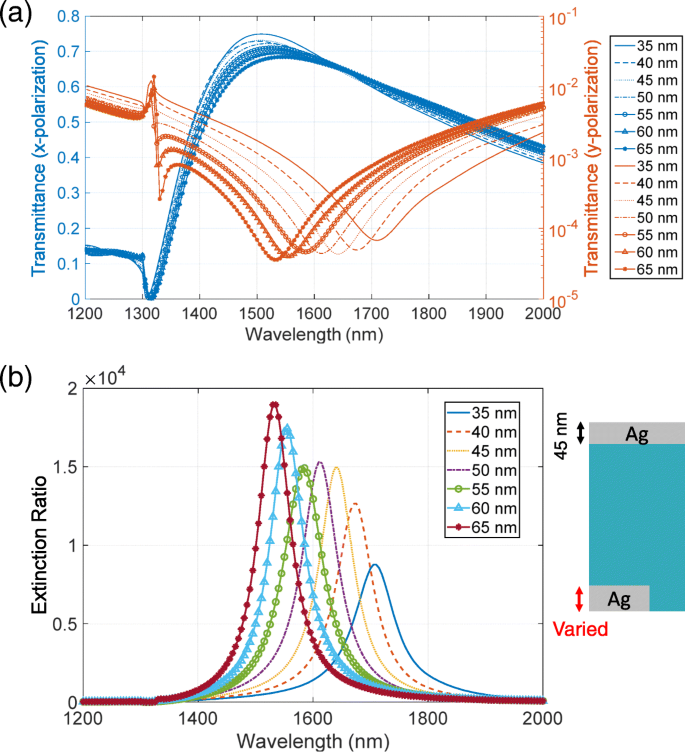
a 透過率と b 相補的な金属層の厚さが異なる場合の消光比スペクトル。最上層の金属層の厚さは45nmに固定され、最下層の厚さは5nm刻みで35から65nmまで変化します（ b の挿入図を参照）。 ）

結論

高性能メタ表面偏光子の劣化特性を調査しました。準備されたメタ表面は、10,000のオーダーの高い消光比を示した。高性能が徐々に低下していることに気づきました。この劣化の原因を明らかにするために、消光比に対する表面形態の影響を調査しました。表面形態を説明するために2つのモデルが提示されました。 1つは、周期曲線とガウスホワイトノイズの組み合わせによって粗い表面をモデル化し、もう1つは、ランダムに分布したナノ粒子によって表面をモデル化します。どちらのモデルも、表面粗さによって高性能が低下しないことを示しています。これは、高い消光比がバビネの原理によって支配され、表面形態の堅牢性がもたらされるためです。また、消光比の急激な低下を示した表面粗さによる消光比と金属損失の増加との関係を調べた。青方偏移のスペクトル特性も数値計算によって再現されており、劣化は金属損失の増加によるものであることを示しています。この結果から、粗さに関連する散乱および粒界損失を低減するために金属蒸着を行う必要があることがわかります。数値計算を通して、透過率が低いと表面形態に対する感度が高くなり、透過率が高いと感度が高くないことがわかりました。これらの知見を利用して、金属層の厚さを変えることで消光比を高めることができると提案した。この研究は、時間劣化に対する高性能と安定性を備えたメタサーフェスの開発への道を開きます。

略語

BS：

ビームサンプラー

GLP：

グランレーザープリズム

NDF：

減光フィルター

OPO：

光パラメトリック発振器

PhC：

フォトニック結晶

SEM：

走査型電子顕微鏡

YAG：

イットリウム鉄ガーネット