熱制御されたRKKY相互作用によるナノ構造の磁気ヒステリシス

背景

Ruderman-Kittel-Kasuya-Yosida（RKKY）タイプの間接交換結合（IEC）[1]と巨大磁気抵抗効果[2]の重要な発見により、多くの新しい基本的な物理学の結果と多数のアプリケーションが生成されました。 [3]。発見されたIECは、金属スタック内の個々の強磁性層の分離に対して大きさと符号が振動し、平行（P）または逆平行（AP）の磁気基底状態を生成します。このRKKYタイプの相互作用は、温度にほとんど依存せず[4、5]、他の外部制御の製造後の影響をほとんど受けないため、効果の使用が制限されます。 RKKYに対する温度の影響を強化し、それを使用してTb / Y / Gd [6]およびCo / Pt [7]多層膜のIECを制御する最近の試みでは、直接平行から逆平行（PからAP）熱スイッチング、幅広い熱遷移（〜100 K）。

最近、磁性多層膜における層間RKKY相互作用のex-situ熱制御の新しいメカニズムを実証しました[8、9]。このアイデアは、キュリー温度が比較的低い（ T ）希釈された強磁性合金の使用に基づいています。 _C ^* ）強​​強磁性（FM）層間の非磁性スペーサーの代わりに。初期設計では、従来のRKKY三層Fe / Cr / FeのCrスペーサーが希釈合金Fe _{x に置き換えられています。} Cr _{100 − x} （図1a、b）。スペーサーが T で常磁性（PM）の場合> T _C ^* （図1a）、3層は、反強磁性（AFM）間接により、Feモーメントの逆平行整列を示します。 交換相互作用（RKKY）。並列配置は、直接によって実施されます。 スペーサーがFM（ T ）の場合の交換相互作用 < T _C ^* ）（図1b）。温度が変化すると、これらの3層は平行から逆平行への磁化スイッチングを示し、磁気近接効果により約100Kのかなり広い遷移を示します[10]。 均一の3層とは対照的 スペーサー、不均一な三層、複合 スペーサーは、約10 Kまでの熱磁気遷移幅で大幅に向上した性能を示します。さらに、スペーサーの特性を調整することにより、逆平行（図1c）または平行基底状態（図1e）のいずれかを T < T _C ^* 。 T 以上の加熱時 _C ^* 、Feモーメントは、Fe / sp1 / Feの場合は平行（図1d）、Fe / sp2 / Feの場合は逆平行（図1f）のいずれかに相互の向きを反転させます。狭い熱遷移と磁気レジーム（P / AP）を選択する機能、および動作温度間隔はすべて、実用的な意味合いの観点から重要な利点です。

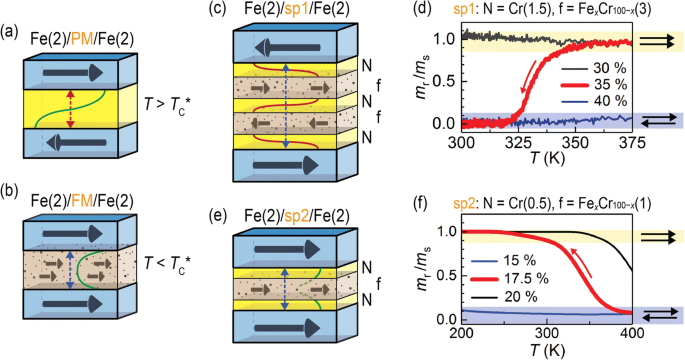
スペーサーが常磁性（PM）の場合のFe /均一スペーサー/ Fe多層膜の磁気レイアウトの図（ a ）または強磁性（FM）（ b ）。 c 、 e 変更された複合スペーサーsp1およびsp2を備えた構造は、それぞれ、低温（ T ）で逆平行および平行の磁気基底状態を示します。 < T _C ^* ）。 d 、 f スペーサーの内部希釈合金層のさまざまな組成に対するスペーサーsp1およびsp2を備えた構造の残留磁化の対応する特徴的な温度変化。層の厚さは「ナノメートル」の括弧内に示されています

多層膜の反強磁性層間結合は、Fe層のモーメントの逆平行整列を反映して、残留磁化がゼロであることを明確に示しています。ゼロ残留磁気に加えて、磁化曲線 M （ H ）は、フィールドスイープを反転する際の飽和とヒステリシスへの階段状のアプローチを特徴としています（図2a）。双線形交換相互作用モデルは M を与えます （ H ）間接交換の有効場で飽和に近づく線として、 H _J 。構造の強磁性層の面内磁気異方性により、飽和の階段状の特性が発生します。その結果、容易軸異方性が1ステップ[11]、4倍異方性が2ステップ連続します[12]。ただし、多層の角度依存の磁気および磁気共鳴の研究では、巨視的な面内磁気異方性は明らかになりません。後者の事実は、モデルシミュレーションを伴う実験結果のより包括的な分析を保証します。以下では、このような包括的なアプローチを使用して、2つの主要な多層設計の磁化スイッチングのメカニズムを、複合スペーサー層（図1c、e）とは対照的に均一（図1a、b）で対比します。

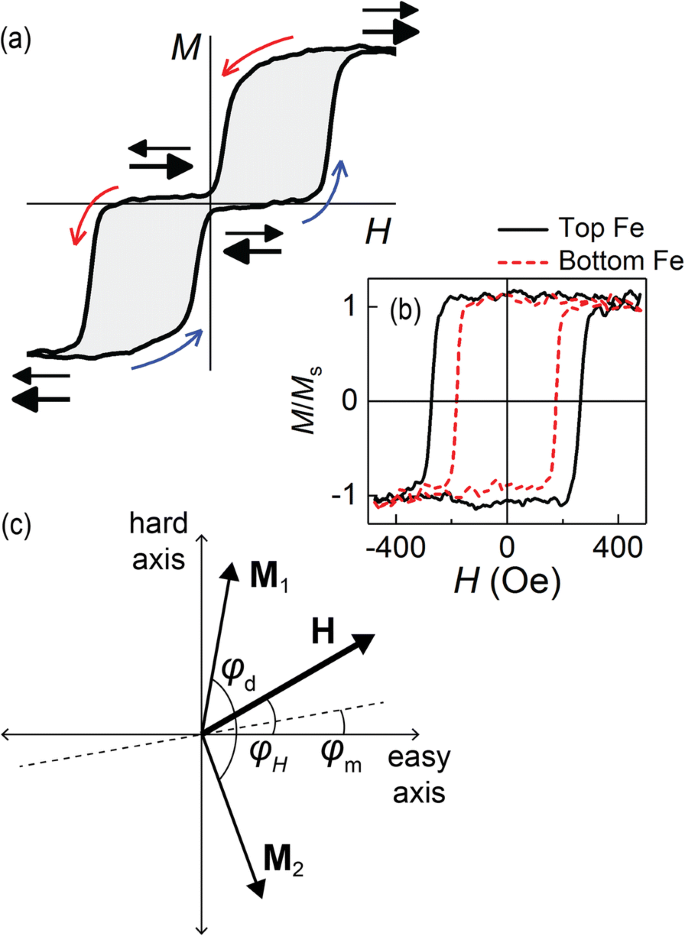
a 典型的な面内磁化曲線、 M （ H ）、反強磁性中間層結合を備えたFe / sp2 / Fe多層膜についてMOKEによって測定されました。曲線の矢印は、フィールドスイープの方向を示しています。水平方向の矢印は、Feの磁気モーメントの相互整列を示しています。 b MOKE M （ H ）参照Fe（2）/ Cr（10）（下部Fe）およびCr（10）/ Fe（2）（上部Fe）二重層のループ。 c 面内 M の参照フレームの概略図 ₁ 、 M ₂ 、および H 、ナノ微結晶の2倍の磁気異方性の容易軸に関して

与えられたシステムの層間交換に関与するメカニズムを理解することの重要性を指摘します。多層膜におけるRKKYの先駆的な研究[13]と、たとえば双二次交換[14、15]へのその拡張は、スピントロニクスとして知られる物理学と技術の主要な発展を開始しました。ただし、元の形式のRKKYは、適切なスイッチングメカニズムがないため、現在は使用されていませんが、フラックスを閉じる参照層などのデバイスで補助的な役割を果たすことがよくあります。この作業では、このような主要なRKKYスイッチングメカニズムを研究し、より具体的には、RKYYの熱オン/オフスイッチングにつながる相互作用間の相互作用を分析します。これにより、磁化のP / APスイッチングの効率が制御されます。ナノ構造。この分析に基づいて、Curie-RKKYナノデバイスのスイッチング性能を最適化するための結論と推奨事項を作成することができます。

メソッド

この作業では、2つの一連のサンプルを分析します：（1）Fe（2）/ sp1（ x =30–40 at。％）/ Fe（2）、ここでsp1 =N / f / N / f / N、N =Cr（1.5）、f =Fe（0.25）/ Fe _x Cr _{100 − x} （3）/ Fe（0.25）（図1c）、および（2）Fe（2）/ sp2（ x =10–20 at。％）/ Fe（2）、ここでsp2 =N / f / N、N =Cr（ d _Cr ）、f =Fe _x Cr _{100 − x} （ d ）、 d _tot =（2 d _Cr + d ）=1.5 nm（図1e）。さらに、多くの参照フィルムと二重層が堆積されました。括弧内の厚さは「ナノメートル」単位です。多層は、DCマグネトロンスパッタリングシステムを使用して、Arで事前にエッチングされたドープされていないSi（100）基板上に室温で堆積された。希釈されたFe _{x の層} Cr _{100 − x} さまざまな組成の二元合金が、別々のFeおよびCrターゲットからの同時スパッタリングを使用して堆積されました。多層製造の詳細については、他の場所で見つけることができます[8、9]。

面内磁気特性評価は、295〜400 Kの温度範囲の高温炉（Lakeshore Inc.）を備えた振動サンプル磁力計（VSM）と磁気光学カー効果（MOKE）を使用して実行されました。 77〜450 Kの温度範囲で光学クライオスタット（Oxford Instr。）を備えた磁力計。さらに、自動ゴニオメーターを備えたXバンドBruker ELEXYS E500分光計を使用して、室温で強磁性共鳴（FMR）測定を行いました。磁気共鳴スペクトルの面内角度依存性。

結果と考察

間接交換相互作用の現象学

F1とF2が強磁性層で、NMが非磁性スペーサーである3層F1 / NM / F2の磁化曲線のシミュレーションに使用される現象論的静磁気モデルには、次の仮定があります。まず、磁場がフィルムの平面に適用されます。これは、私たちの実験に対応し、計算を簡素化します。第二に、多結晶膜の個々の粒子は、容易軸がすべての面内角度にわたって均一に分布している2倍の面内異方性によって特徴付けられます（膜は面内回転下で堆積されました）。これらの仮定は、調査対象のシステムにとって妥当であり、測定された M に最もよく適合します。 （ H ）以下で説明するさまざまな温度でのデータ。

F1 / NM / F2システムの自由エネルギー密度は次のように記述できます

ここで U _H 、 U _a および U _J それぞれ、フィールド H のFM層のゼーマンエネルギーです。 =（ H 、φ _H ）、一軸異方性エネルギー、および双線形タイプの層間結合エネルギー[16、17]。 FM層の磁気モーメント M ₁ =（ M 、φ ₁ ）および M ₂ =（ M 、φ ₂ ）は、図2cに示すように、同じ大きさです。 H _a1,2 および H _J は、それぞれ一軸（2倍）異方性と双線形層間結合の有効場です。角度変数への変換φ _m =（φ ₁ + φ ₂ ）/ 2およびφ _d =（φ ₁ − φ ₂ ）システムの磁気自由エネルギーの式を簡略化して

次のシミュレーションでは、磁化曲線 M （ H ）、パラメータφを見つけることによって得られます _m およびφ _d 、 U の最小値に対応します （2）で与えられたφ _H 、 H _1a 、 H _2a 、および H _J 、によると

磁化の保磁力

測定された M （ H ）AFM交換相互作用を備えた構造の場合、ステップ状の形状であり、反転フィールドスイープの保磁力が明確に定義されています（図3a）。上記の現象論的モデルは、強磁性層Fe（2 nm）の磁気特性と、層間結合を媒介する複合スペーサーの熱誘導磁気遷移の両方を分析するために使用されます。

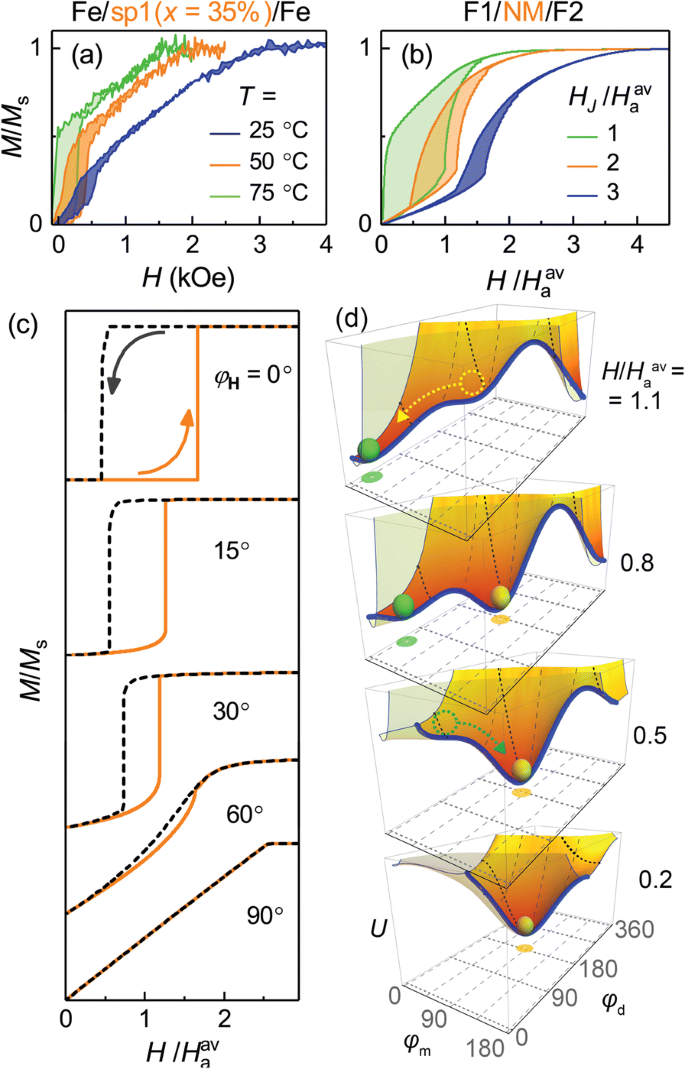
a 測定された M （ H ）系列からのサンプルの曲線、Fe / sp1（ x =15％）/ Fe、さまざまな温度で。 b 対応するシミュレートされた M （ H ）有効場の強度が異なる場合のモデルF1 / NM / F2三層の曲線 H _J 間接交換相互作用の。 （ H _a ^av =（ H _a1 + H _a2 ）/ 2、ここで H _a1 および H _a2 層F1とF2の異方性フィールドです。 c M （ H ）選択した角度で​​シミュレートされた曲線φ _H 、 H の場合 _J / H _a ^av =2. d 適用された場の関数としての自由エネルギーの極小値の変換（2） H 、ケース H の場合 _J / H _a ^av =2およびφ _H =15°。青い線は、さまざまなφのエネルギー最小値を結ぶパスをトレースします _m （φ _d ）。エネルギー面の前面は、イラストを視覚的にわかりやすくするために透明です

単結晶基板上に成長したエピタキシャル（100）Feベースの多層膜は、通常、4倍の面内磁気異方性[12]を特徴としますが、他のテクスチャの基板[たとえば、（211）]は2倍の異方性をもたらす可能性があります[11]。 M の主な違い （ H ）2つのケースの間には、 M に2つの特徴的なステップがあります。 対 H 異方性が4倍で、 M が1つしかない場合 -vs- H それが2つあるときのステップ。参照Fe（2 nm）フィルムとFe / Cr / Fe三層のVSMおよびFMR研究（データは示していません）では、ヒステリシスループまたは共振スペクトルに有意な面内角度依存性は見られず、結論を導き出しました。本質的に巨視的な面内磁気異方性は存在しません。一方、上記の数値解析では、測定されたワンステップ形状の M （ H ）RKKY結合Fe / Cr / Fe三層のループは、多結晶膜を形成する個々の微結晶のスケールでの2倍の磁気異方性によるものでなければなりません。フィルム面内の局所異方性容易軸の均一な角度分布は、サンプルの場合、回転する基板への堆積に起因する可能性があります。このような磁気異方性のパターンは、スパッタされた多層膜の多結晶性とナノ結晶粒子間の面内ひずみ変動の観点から説明できます[18]。

M （ H ）モデルシステムF1 / NM / F2の曲線、AFM層間交換結合のさまざまな強度（有効場 H ）でシミュレート _J ）および図3bに示されているように、実験曲線（図3a）に見られるすべての主要な機能を示しています。 M （ H ）Fe / sp1（ x の場合 =35 at。％）/ Feは、温度の上昇とともに大幅に変化します。この変化は、シミュレーションされた M と直接比較できる層間結合の弱体化によるものです。 （ H ）図3bに示されています。実験的な M で見られたすべての変化 （ H ）層間結合が弱くなるにつれて保磁力が向上することを含むデータは、モデルを検証するシミュレーションされた動作と非常によく相関しています。モデルの計算は、温度の影響を直接考慮せずに実行されることに注意してください（効果的に低減された H を介してのみ） _J ）、これは個々の層の保磁力を低下させるはずです。これが、実験の保磁力がやや小さくなる原因である可能性があります。

シミュレートされた M （ H ）図3bに示す曲線は、 M を平均して得られたものです。 （ H ）さまざまな角度で計算φ _H 外部フィールド H の間 そして一軸磁気異方性の容易軸。図3cは、選択した角度φでの曲線を示しています。 _H H の場合 _J / H _a ^av =2.ここで、 H _a ^av =（ H _a1 + H _a2 ）/ 2、ここで H _a1 および H _a2 は、それぞれF1層とF2層で作用する面内一軸異方性の有効場です。比率 H _a1 / H _a2 計算に使用される=0.7は、実験的に得られた値に対応します（図2b）。階段状の形状と保磁力は、φに対して明確に定義されています。 _H <60°。上記のように、参照Fe（2 nm）フィルムとFe / Cr / Fe三層の追加のVSMおよびFMR研究では、ヒステリシスループまたは共振スペクトルに有意な面内角度依存性は見られませんでした。 VSMとFMRはサンプルの積分特性を測定するため、巨視的な面内磁気異方性は本質的に存在しないと結論付けます。一方、観測された保磁力は、面内の磁気異方性にのみ起因する可能性があります。さらに、実験的な M の形状 （ H ）曲線は、選択したφの個々の曲線ではなく、平均化によって得られた計算された曲線に近くなります。 _H 。したがって、スパッタされた多層膜の多結晶性を考慮すると、Fe（2 nm）層は、膜面内の局所異方性容易軸の均一な角度分布を持っていると結論付けることができます。

図3dは、エネルギー U （φ _m 、φ _d ）式の H に応じて2つの変更 。繰り返しになりますが、 H _J / H _a ^av =2およびφ _H =15°、これはパネル（c）の2番目の曲線に対応します。図3dの太い実線は、さまざまなφのエネルギー最小値を結ぶ経路を示しています。 _m （φ _d ）。極小値は、この最小値のパス内で明確に定義されています。低磁場での最小値は、Feモーメントの逆平行配向に対応します（φ _m ≈90°、φ _d ≈180°）。 H の増加に伴い 、2番目の極小値が現れて深くなり、最初の極小値は浅くなり、最終的には消えます。この単一最小状態は、Feモーメント（φ）の平行配向に対応します。 _m ≈φ _H 、φ _d ≈0°）。その後減少する H 、システムは、 H が低くなるまで、最初は2番目に小さい（平行磁気状態）状態にあります。 そして、システムは最初のエネルギー最小値（逆平行状態）になります。

直接交換相互作用と間接交換相互作用の競合：磁気保磁力の温度依存性

最初の一連の3層Fe / sp1 / Feは、低温AFM中間層結合から高温分離状態への熱誘導遷移を示しますが、2番目のシリーズは低温FMから高温AFMへの遷移を示します。カップリング。 2番目のケースのFMからAFMへの熱遷移では、外部磁場は不要であり、磁化の切り替えは完全に可逆的です。これは、アプリケーションにとって重要な利点です。

最初の一連のサンプルの上記の分析を通じて検証されたモデルを使用して、次に、Fe / sp2 *（ x ）における直接および間接の層間交換結合間の競合の調査に焦点を当てます。 ）/ Fe、タイプsp2 * =Fe _{x の均一なスペーサー付き} Cr _{100 − x} （1.5 nm）およびタイプsp2 * =Cr（ d の複合スペーサー _Cr ）/ Fe _x Cr _{100 − x} （ d ）/ Cr（ d _Cr ）、 d + d _Cr =1.5 nm（sp2 *は厚さ固定スペーサーsp2 =Cr（0.4）/ Fe _{x から派生したものです} Cr _{100 − x} （0.7）/ Cr（0.4）第2シリーズ）。図4は、実験的な M を比較しています。 （ H ）sp2 =Cr（0.4）/ Fe ₁₅ の構造のループ Cr ₈₅ （0.7）/ Cr（0.4）[パネル（a）]および対応する M （ H ） H でシミュレートされた曲線 _J 実験に最適なものを取得するなどの選択。最初に注目すべきは、計算されたループと測定されたループの類似性が高く、すべての主要な機能が再現されていることです。次に、実験では、FM中間層カップリング[図4aの低温シングルループ]からAFMカップリ​​ング[図4aの残留磁気がゼロの高温ループ]への温度誘導遷移が示されています。さまざまな有効結合場の値 H に対するシミュレートされたループの形状の変化 _J （図4b）は、選択した現象論的記述の妥当性をさらに確認します。前のセクションと同じ、 H _a1 / H _a2 =0.7がシミュレーションで使用されました。ここではそうではありませんが、階段状の M （ H ）AFM中間層結合による形状（たとえば、300Kおよび H でのループ） _J =0.5 H _a ^av ）原則として、層間結合がない場合のF1とF2の異なる強制場によって引き起こされる可能性があります（ H _J =0）。ただし、強力なFM中間層結合は、常に単一の M になります。 （ H ）ループ。

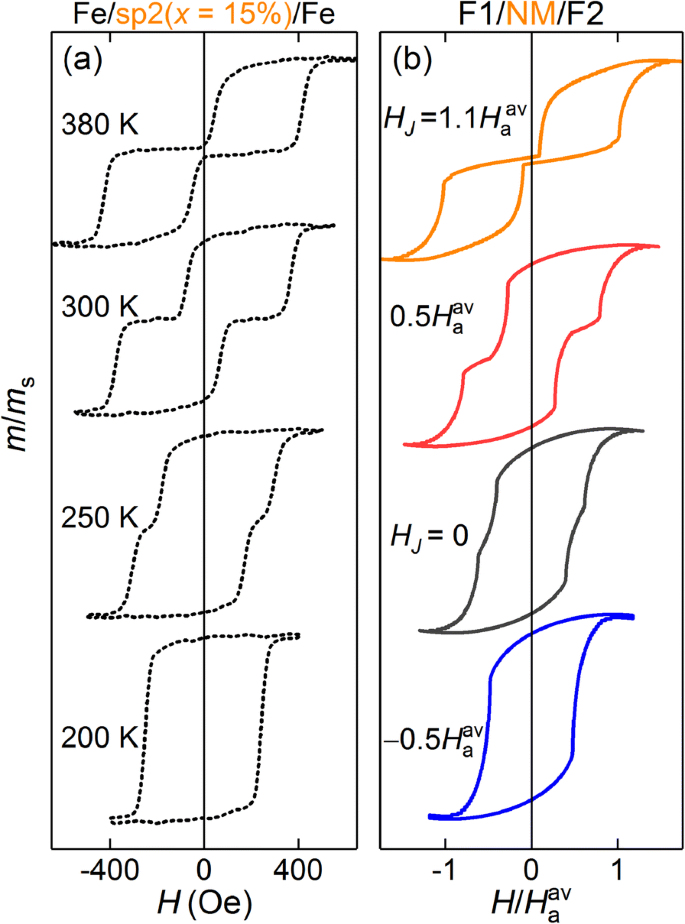
a 2番目のシリーズFe / sp2（ x ）のサンプルについてMOKEによって測定された磁化対磁場 =15％）/ Fe、さまざまな温度で。 b 対応するシミュレートされた M （ H ）モデルF1 / NM / F2三層の曲線、間接交換結合のさまざまな有効場、 H _J

部分ループの保磁力（ H _c ^パート ）はすべてのサンプルで顕著な温度依存性があり、温度の低下とともにほぼ直線的に増加します。図5aは、磁化導関数d M の2つのピークの磁場の差として定義される強制磁場の温度依存性を示しています。 / d H vs H 。 x のシリーズ =15％には、スペーサーを構成する層の厚さが異なるサンプルが含まれています： d （ d _Cr ）=3（6）、7（4）、9（3）、11（2）、15（0）Å。最後のサンプル[ d （ d _Cr ）=15（0）Å]は、均一なスペーサーFe ₁₅ を備えた3層です。 Cr ₈₅ （1.5 nm）。 d のサンプル ≤7Å（ d _Cr ≥4Å）は、 H の単調な増加を示します _c ^パート 温度が下がると。 d が小さいサンプルの保磁力 _Cr （<4Å）は、転移温度のすぐ下でこの勾配から逸脱し始めます。 H の高温部分 _c ^パート （ T ）ただし、一般的な線形傾向にあります[図5aに太い赤い線で示されています]。温度に対する保磁力のこの線形勾配は、主に外側のFe（2 nm）層の固有の保磁力の変化に関連しています。

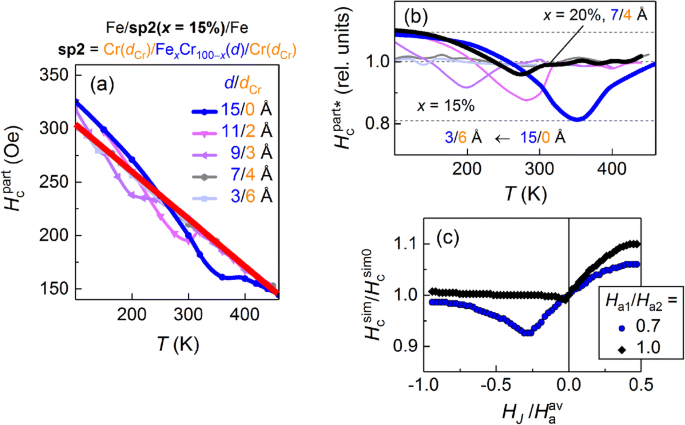
a 部分ループの保磁力の温度依存性（ H _c ^パート ）構造体Fe / sp2（ x =15％）/ Feの厚さが異なるFe _x Cr _{100 − x} およびCr層（ d および d _Cr 、それぞれ）スペーサーsp2で。赤い太い線は、 H の高温部分の線形近似です。 _c ^パート （ T ）。 b 線形バックグラウンドに正規化された保磁力の温度依存性。 c 保磁力と H _J シミュレートされた M から取得 （ H ）2つの場合の曲線：（1） H _a1 / H _a2 =0.7および（2） H _a1 = H _a2

以前の研究[9]では、スペーサーの厚さが d の構造 ≤7Å（ d _Cr ≥4Å）は、最も鋭い熱磁気スイッチングを示しました。次に、このような磁気遷移の狭まりの理由は、外側のFe層間の直接交換チャネルをオフにすることであると示唆しました。一方、 H の依存性 _c ^パート* vs T （図5b）、 H を正規化して得られたもの _c ^パート （ T ）傾斜した固有保磁力の背景に対して、顕著な負のを示します 薄いCrスペーサーを備えた構造のみの偏差（ d _Cr <4Å）、 d の偏差は基本的にありません _Cr ≥4Å。 x の依存関係 =20％、 d _Cr x の遷移のため、比較のために=4Åが示されています =15％、 d _Cr =4Å（ T _C ^* ≈140K）は最低測定温度に近いです。 H に負の偏差がない _c ^パート* vs T d の構造の場合 _Cr ≥4Åは、直接層間結合が完全に抑制されていることの追加確認として役立ちます。

依存関係の一部を分離して分析するには H _c ^パート （ T ）、これは層間結合の強度と符号の変化によって駆動されます（ H _J ）、シミュレートされた M の保磁力 （ H ）は H に対してプロットされます _J 図5c。このようにして得られた H _c ^sim vs T F1層とF2層の有効異方性場の比率 H に依存します _a1 / H _a2 。 H の偏差が大きい _a1 / H _a2 ユニティから、最小値が深くなり、ダイアグラムのFM側のゼロフィールドからのオフセットが大きくなります（ H _J <0）。異方性フィールドが等しい場合（ H _a1 / H _a2 =1）、最小値は存在しません。この動作は、 H の違いに似ています。 _c ^パート* （ T ） d が大きい均一で複合的なスペーサーを備えた構造の場合 _Cr （≥4nm）[それぞれ図5bの青と黒の曲線]。これは、これら2つのタイプのスペーサーが2つの外側のFe層の間の層間結合を異なる方法で伝達することを示しています。均一なスペーサーでは、直接FM交換は間接AFM交換と競合し、ある温度で H _J =0.このケースは、F1層とF2層の異方性フィールドが異なるモデルでよく説明されています[図5cの青い曲線]。対照的に、複合スペーサーを備えた構造内のFe層は、低温でFe / Cr / FeCrおよびFeCr / Cr / Feを介して順次FM結合され、スペーサーのFeCr内層はFM状態になります。このFeCr層は追加の交換リンクとして機能するため、スペーサーは、外側のFe層の保磁力を効果的に等しくするように交換を伝達します[図5cの黒い曲線]。 FeCr層が常磁性状態にあるとき、システムは均一なスペーサーを備えたものと同様に動作します[ H の高温部分 _c ^パート* vs T 図5bの依存関係と H のAFM側 _c ^sim vs T （ H _J > 0）図5c]。

結論

要約すると、我々は、異なるタイプの層間交換媒介スペーサーを有する多層における温度誘起磁化スイッチングの２つのメカニズムを説明し、比較した。スイッチングメカニズムは、均一なスペーサーを介した直接および間接の交換相互作用、または複合スペーサーを介した強磁性および反強磁性タイプの全間接交換相互作用の競合を反映しています。スペーサー設計の重要な要素は、弱磁性の希薄合金層であり、そのキュリー遷移は、構造内でP-AP磁化スイッチングに変換されます。多層膜の磁気ヒステリシスの詳細な理論シミュレーションによってサポートされている測定データは、容易軸が外側の強磁性層の平面に均一に分布している一軸磁気異方性のナノ粒子によるものとして説明されています。磁気遷移領域での保磁力の温度依存性は、スペーサーの設計ごとに異なる形をしています。複合スペーサーを備えた構造の特定の動作は、抑制された直接層間交換チャネルの結果であることがわかり、関連するP-APスイッチングメカニズムは、間接強磁性と間接反強磁性（両方のRKKYタイプ）交換の競合です。

したがって、スペーサー内の直接層間交換の壊れたチャネルが、より鋭い熱磁気遷移と相関していることを示した。さらに、スペーサー内の近接効果が作用しない、純粋に間接的な層間交換、強磁性RKKYと反強磁性RKKYの熱駆動の競合が、さらに優れたスイッチング性能につながることを示しました。これらの結果は、スピン熱電子デバイスにおけるCurie-RKKYナノ構造のデバイスアプリケーションにとって重要であるはずです[19、20]。

略語

AFM：

反強磁性

AP：

逆平行

FM：

強磁性

FMR：

強磁性共鳴

IEC：

間接交換相互作用

MOKE：

磁気光学カー効果

NM：

非磁性

P：

並列

PM：

常磁性

RKKY：

Ruderman-Kittel-Kasuya-Yosida

VSM：

振動試料型磁力計