円偏光によって駆動されるプラズモン二量体のスピンと軌道回転

背景

直線偏光（LP）光で照射された2つの微粒子（MP）またはナノ粒子（NP）の光結合は、光と物質の相互作用の結果である重要なオプトメカニカル挙動です[1,2,3,4]。光学的に結合した二量体の間には、いくつかの安定した平衡粒子間距離があります。これらの距離は、媒体の波長のほぼ整数倍です[3,4,5,6]。さらに、二量体の配向は、LP光の偏光に垂直です。粒子間距離は波長の整数倍に近いため、粒子間の散乱光子は建設的な干渉を起こし、結合力を誘発します。複数のシリカMPまたはAgNPの光学的に結合したアレイの現象も研究されました[7、8、9、10]。円偏波（CP）平面波の照明については、Haefner etal。サイズが100〜700nmの2つの結合シリカNPの縦方向のスピンと軌道回転のヘリシティは、入射光の利き手と同じであると報告されています[11]。最近、Sule etal。実験的に、光学力によって束縛された半径75nmの2つのAgNPの軌道回転のヘリシティは、水中で790nmの集束CPガウスビームの利き手と反対であることがわかりました[12]。つまり、Agダイマーは負の光学軌道トルクを受けます[13、14]。さらに、測定された軌道回転は約4kHzでした[12]。一方、CPガウスビームによって引き起こされる半径100nmの単一のAuNPのスピンも研究されています[15、16、17、18]。測定されたスピン回転は3.5kHzと高かった[15]。ここ数十年で、光場の縦/横スピン軌道相互作用（SOC）が多くの注目を集めています[19、20、21、22、23]。たとえば、光渦ビーム（たとえば、方位角または放射状の偏光を持つ高次ラゲールガウスビーム）または高度に集束されたCPガウスビームを使用して、SOCを誘導することができます[24、25、26、27、28、29、30 、31、32、33、34]。光渦ビームのねじれた電磁（EM）場は、スピン角運動量と軌道角運動量の両方を運び、それによって、近くのプロービングNPの縦/横スピンと軌道回転を誘発します[18、19、20、21、22、23 、24、25、26]。特に、AuまたはAg NPの近接場でのSOCは、これらのNPでの自由電子の集団運動（プラズモン効果）により、より重要になります[28、29、30、31]。

この論文では、CPガウスビームの照射によって誘導される、基板によって支持された2つの結合されたAu NP（二量体）のオプトメカニカル挙動（光学力とトルク）を理論的に研究します。基板は、3D空間に浮かぶのではなく、焦点面内を移動するこれらの自立型NPを閉じ込めるために必要です。多重極（MMP）法を使用して、電磁界を数値的にシミュレートし、光学的に結合した二量体の光学軌道とスピントルクを分析します[35、36]。二量体のオプトメカニカル応答を通じて、縦方向/横方向のSOCが現れます。特に、二量体に負の光軌道トルクを発生させる条件についても調査します。

メソッド

図1は、基板でサポートされ、垂直に入射する左手（LH）CP光（平面波またはガウスビーム）で照射された1対の同一のAu NPの構成を示しています。ここで、 d 粒子間距離を表します。ガウスビームのウエストは w で表されます ₀ 、および焦点面はAuNPの中央断面積にあります。平面波とガウスビームの電界の定式化は付録として添付されています。基板の屈折率は周囲の媒体である水の屈折率と同じであると仮定します。したがって、反射光は媒体と基板の間の界面で誘導されません。基板の存在によって光場が乱されることはありません[37]。一方、基板の存在は、基板上を移動するNPをサポートするための閉じ込めとして機能します。多重極（MMP）法は、誘導電磁界をシミュレートするために使用されます[17、18、35、36]。光学力 F ^j j に作用 th NP（ j =1、2）は

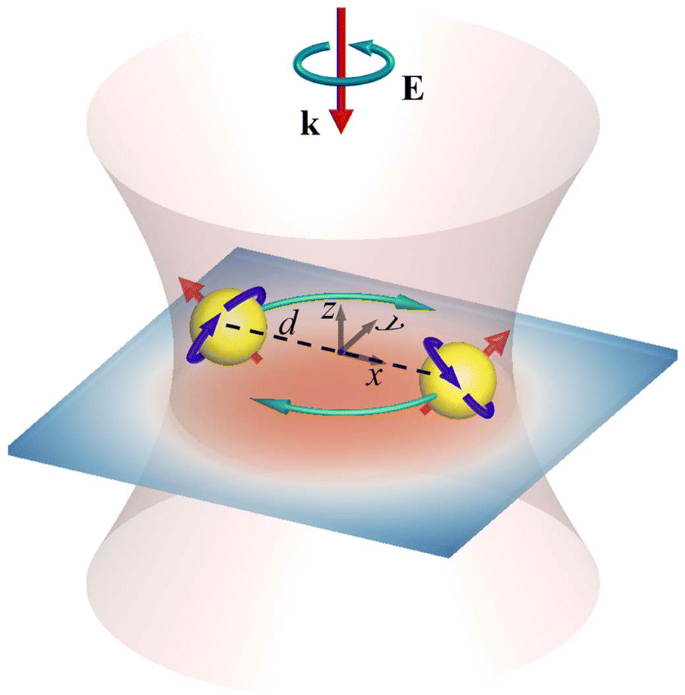
垂直に入射する腰のLHCPガウスビーム（w0）によって照射された、支持基板を備えた一対のNPの構成。これらのNPの中央断面はガウスビームの焦点面にあり、dはNPの中心間の距離です。オプトメカニカル応答は、縦方向の軌道回転と縦方向/横方向のスピンです

ここでは、 n j の表面の外向きの法線ベクトルです。 th NP、および T は時間平均マクスウェル応力テンソルで表されます

式で。 （2）、私 は3×3単位行列であり、オーバーバーは複素共役を示し、Reは実数部を示します[17、18、35、36]。ここで、ε およびμ 周囲の媒体の誘電率と透磁率です。 E に注意してください および H 式に使用される外部合計フィールドです。 （2）。実際、 T また、時間平均線形運動量フラックスです。このホワイトペーパーでは、光学力は円筒座標で表されます。半径、方位角、および z -軸コンポーネント。半径方向の力は、2つのNP間の引力または反発力を示し、方位角方向の力は、NPの公転のヘリシティを示します。

一方、 j の光学スピントルク th NP（ j =1、2）個々のNPの回転は、

式で。 （3）、 x ^j × T は角運動量フラックスであり、 x ^j は点 x の相対位置ベクトルです 表面に S _j j の重心\（{\ mathbf {x}} _ c ^ j \）に関して th NP; \（{\ mathbf {x}} ^ j =\ mathbf {x}-{\ mathbf {x}} _ c ^ j \）。長手方向は、光軸に平行になるように指定されています（たとえば z 入射光の方向）であり、横方向は光軸に垂直です。一方、 z の縦方向の光学軌道トルク 方位角光学力によって引き起こされる各NPの方向は、 F として定義されます。 _θ d 円筒座標で/ 2。 λでのAuの比誘電率 =シミュレーションで使用される800nmは（− 24.062、1.507）[38]です。

結果と考察

半径100nmの2つの同一のAuNPに加えられる光学力とトルクを、垂直に入射するLHCP平面波または焦点面に集束されたガウスビームで照射して調べます。周囲の媒体は水です。中心での平面波またはガウスビームのフルエンスは25MW / cm ² 。仮想基板によってサポートされている2つの自立型NPの中心は、 xy 内を移動できます。 平面（焦点面）。光学力（ F _r 、 F _θ ）対粒子間距離 d CP平面波またはウエストが500nmのλの集束ガウスビームの場合 =800 nmをそれぞれ図2a、bに示します。これらのNPの中央断面は、ガウスビームの焦点面にあります。図2aは、平面波の場合、 F で安定した平衡粒子間距離がいくつかあることを示しています。 _r =0および負の勾配。最初のもの d ₁ 603 nmで、2番目は d ₂ 1204nmで。これらの「安定平衡」粒子間距離は、媒体中の波長のほぼ整数倍です。つまり、 d _m =mλ / n 、ここで n は媒体の屈折率であり、 m =1、2、3 ...これは光結合力によって引き起こされる長距離の光と物質の相互作用の結果です。これは、2つのNPを接続する光学ばねがあることを示唆しています。復元力 F _r 光学ばねの特性により、これらの安定した平衡粒子間距離でNPが互いに離れた状態に保たれます。ガウスビームの場合、最初の2つの安定平衡粒子間距離 d ₁ および d ₂ 図2bに示すように、それぞれ585nmと1131nmであり、ガウスビームによって誘導される勾配力のため、平面波よりもわずかに小さくなっています。

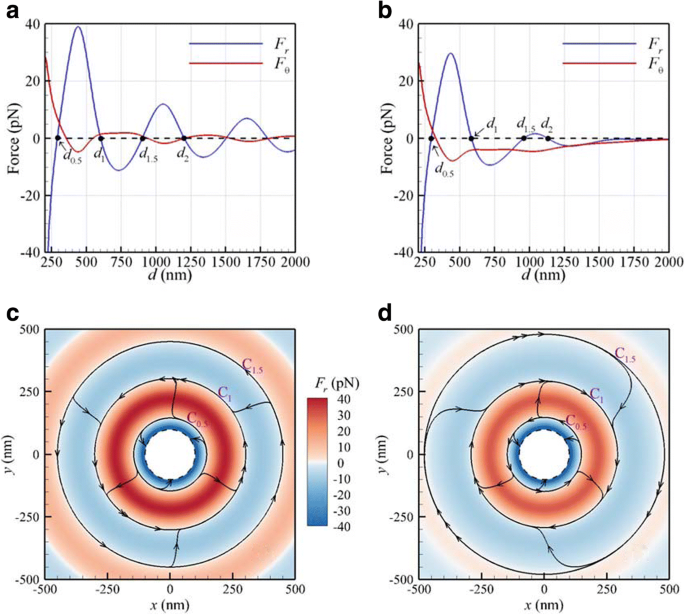
光学力（ F _r 、 F _θ ）対 d λの場合 =CP a による800nm 平面波と b 焦点面でウエストが500nmのガウスビーム。光学力の2D流線型マップ（ F _r 、 F _θ ）CP c によって誘発される 平面波と d ガウスビーム。カラーバーは F の振幅を表します _r 。破線のリングは、NPが接触している2つのNPの中心の限界円です

実際、縦軌道トルク F _θ d / 2は、これらのNPを駆動して、直径 d の軌道で回転させます。 ₁ および d ₂ 。ガウスビームの場合、軌道はビーム軸を中心とします。方位角光学力の符号（ F _θ ）は、ガウスビームによって誘発された最初の安定平衡軌道での縦方向の軌道回転（回転）が平面波によるものと反対であることを示しています。これは、負の F であることを示しています _θ CPガウスビームの負の軌道トルク F を生成します _θ d ₁ / 2最初の安定平衡軌道で;さらに重要なことに、Au二量体の軌道回転のヘリシティは入射CP光の利き手と反対です[12]。 F に注意することも興味深いです _θ d のように常に負です ガウスビームの場合は> 300nm。負の軌道トルクによる光学的に結合されたNPの逆回転（回転）の現象は、光ピンセットシステムで簡単に観察されます。負の光軌道トルクは、ガウスビームのねじれた電磁場に起因する可能性があります[23]。

力 F によって駆動される球のストークスの法則によると 粘性流体内を移動するには、終端速度 v _T は v _T = F /（6 πrη ）、ここでη は水の動的粘度（0.001 kg / m s）です。これは、加えられた力が粘性流体の抗力と釣り合った結果です[39]。ストークスの法則に基づいて、粘性媒体中のNPの終端速度ベクトルは加えられた力に比例します[39]。したがって、これらのNPの軌道とほぼ同等の流線を取得するために、光学力場を使用しました。さらに、光学力ベクトル場（ F ）から直接取得された2D流線マップ _r 、 F _θ ）NPに及ぼす影響は、平面波とガウスビームのそれぞれについて、図2c、dにプロットされています。ここで、カラーバーは F の振幅を表します。 _r 。各点での流線の接線は、光学力ベクトルに平行であり、したがってNPの速度にも平行であることに注意してください。粒子間距離範囲が小さい場合（ d < d _0.5 ）、半径方向の光学力 F _r は負であるため、図2c、dに示すように、これら2つのNPは互いに引き付け合って最終的に衝突します。破線のリングは、NPが接触している2つのNPの中心の限界円です。内側の環（青）は、短距離相互作用の領域です。内輪 C _0.5 内側の環の間（青、負の F _r ）および2番目の環（赤、正の F _r ）は、Au二量体の短距離と長距離の相互作用領域間の境界線です。 C の直径 _0.5 d です _0.5 =図2cおよび d の291nm _0.5 =図2dの296nm。遠距離（ d _0.5 < d < d _1.5 ）、半径方向および方位角方向の光学力により、2つの結合されたNPが駆動され、最初の安定平衡軌道 C に近づきます。 ₁ 直径 d ₁ 光学的結合力の影響による。光学的に結合したAu二量体は軌道 C に沿って反時計回り（CCW）に回転します ₁ （ d ₁ =603 nm）図2cでは、 C に沿って ₁ （ d ₁ =585 nm）図2dの時計回り（CW）。前者の回転は、正の軌道トルク（ F ）によって引き起こされる入射光の利き手と同じです。 _θ > 0）、後者は負の軌道トルク（ F ）のために逆になります _θ <0）。 CP平面波（ここには示されていません）が照射された603 nmの安定平衡距離を持つダイマーの散乱断面積スペクトルの分析によると、光学的に結合したダイマーの結合表面プラズモン共鳴（SPR）はほぼ入射光に対応する800nm。これは、単一のNP（530 nm）のオフレゾナンスです。一般に、二量体の結合SPRは粒子間距離に依存します。距離が大きいほど、二量体の結合SPRが赤方偏移します。より長い波長のガウスビーム（1064 nmなど）を使用すると、安定平衡粒子間距離が増加します。ただし、2つのNP間の距離が大きくなりすぎると、光結合効果が低下し、結合SPRが徐々に消えます。その結果、530nmでの単一NPのSPRが支配的になります。

直径 d の軌道に沿って移動する半径100nmのAuNPの場合 角速度Ω _z 、速度はΩ _z d / 2 = F _θ /（6πrμ ）。ガウスビームが適用されている場合（ F _θ =− 4 pN）、角速度Ω _z （1秒あたりのサイクル数） C に沿って ₁ 約− 7kHzです。桁違いは実験結果と一致しています[12]。 r の2つのAgNPの軌道回転の角速度 =14mWのガウスビームで照射された75nmは-4kHzです。 d の場合 _1.5 < d < d _2.5 、これらのNPは、二次安定平衡軌道 C に近づき、それに沿って回転します。 ₂ （ここには表示されていません）。これらの場合、 F の光学力に注意してください。 _z 放射圧のためにこれらのNPを下流に押し出すのは負です。 F _z =− 161.3 pN（平面波の場合）および− 117.2 pN（ガウスビームの場合）。これは、 F の駆動光学力のバランスをとるために、支持基板からの反力が必要であることを示唆しています。 _z 。したがって、 z の合力 これらのNPの方向はゼロです。これらの2つのNPは、 xy 内を移動するように制限されています 焦点面の平面。

一方、図3a、bは、光学スピントルク（ M ）を示しています。 _r 、 M _θ 、 M _z ）対 d 焦点面でそれぞれ平面波とガウスビームによって誘導されます。これら2つのNPの結果は同じであるため、ここでは一連の光スピントルクのみがプロットされています。前の2つ（ M _r 、 M _θ ）は横方向のスピントルクであり、後者は M _z 縦方向のものです。縦方向のスピントルクのヘリシティは、どちらの場合も入射光の利き手と同じであることがわかります。これは、入射CP光の吸収された光子の角運動量が回転と軌道回転のためにこれらのNPに伝達されるためです。横方向の光学スピントルク（ M _r 、 M _θ ）ガウスビームによって誘発されるものは、平面波によって誘発されるものと比較して非常に大きくなります。これは、ガウスビームの焦点面でのねじれた電磁場の横成分に起因する可能性があります。さらに、光学的横方向スピントルクの最大の大きさは、おおよそ最初の安定平衡軌道 C で発生します。 ₁ （ d ₁ =585 nm）、図3bに示すように。トルク M で回転する回転する球のストークスの法則によると 粘性流体では、球の最終角速度はωです。 _T = M /（8 πr ³ μ ）[18]。したがって、 C でのNPの縦/横スピン角速度の大きさ ₁ は約10kHzであり、その桁数は測定された縦方向のスピン速度[15]、約3.5kHzと一致しています。要約すると、上記の現象は、図１および２に示されるように。 2bと3bは、縦方向の軌道回転が縦方向/横方向のスピンを伴うことを示しています。 2つの結合されたNPの動きは、連星系の動きに似ています。ここでは、光学力がこれらのNPの結合力と軌道駆動力を提供し、光学スピントルクがそれらの回転を引き起こします。

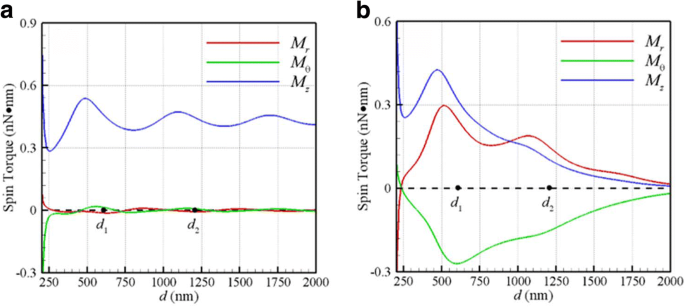
光学スピントルク（ M _r 、 M _θ 、 M _z ）対 d λで = a の場合は800nm 平面波と b w のガウスビーム ₀ =焦点面で500nm

さらに、光ピンセットの対象物の虹彩を調整して入射ビームのサイズを変更し、それによって開口数とガウスビームのウエストを変更することができます。図4aは、光学軌道トルク F を示しています。 _θ d 対応する最初の安定平衡軌道（ d ）で回転する半径100nmの2つの結合されたAuNP上の/ 2 = d ₁ ）対λのCPガウスビームのウエスト =800nm。対応する最初の安定平衡距離 d ₁ は図4a（右側のスケールバー）にもプロットされており、平面波は w の特殊なケースとして扱うことができます。 ₀ →∞。正の軌道トルクと負の軌道トルクの間のガウスビームのウエストのターニングポイントは1150nmで、 F に対応します。 _θ =0、図4aに示すように。ガウスビームのウエストが小さいほど、負の軌道トルクの大きさが大きくなります。ウエストが大きくなると、 d ₁ ガウスビームの値が平面波（ w ）の値（603 nm）に近づく ₀ →∞）。特に、ウエストが減少すると、横方向のスピントルクの大きさ（ M _r 、 M _θ ） d で ₁ 縦方向のスピントルク M が大幅に増加しますが、 _z 図4bに示すように、減少します。これらの結果は、ガウスビームのウエストが、電磁場の歪みの程度により、負の縦軌道トルクと横スピントルクを誘発する重要な要因であることを示しています。

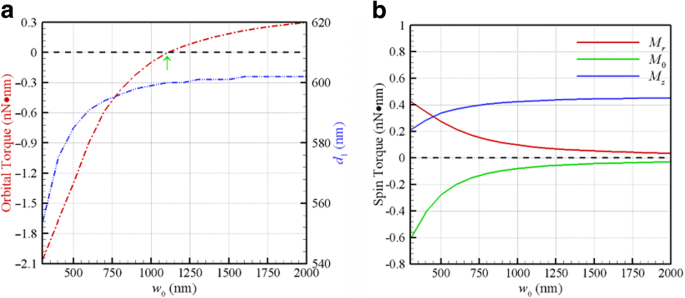
a 光学軌道トルクと d ₁ λのガウスビームのウエストに対する最初の安定平衡軌道で =800nm。正または負の軌道トルクを生成するためのウエストのターニングポイントは1150nmです。 b d でのウエストに対する光学スピントルク ₁

これらのNPの負の軌道回転と横方向の回転のメカニズムは、光ビームの軌道角運動量の寄与がなくても、ライトフィールドのスピン角運動量の回転に起因する可能性があります[23]。負の縦軌道トルクとAu二量体の横スピントルクの性能を通じて、光子のプラズモン増強SOCを明らかにすることができます。さらに、二量体の軌道回転の方向と個々のNPのスピンは、入射光の利き手によって異なります。

結論

CP光を照射したAuNPのペアのオプトメカニカル応答（光学力とトルク）を理論的に研究しました。我々の結果は、それらの回転（回転）のための安定平衡軌道が長距離相互作用のために誘発されることができることを示しました。安定平衡粒子間距離は、媒体中の波長のほぼ整数倍です。方位角の光学力はこれらのNPの軌道回転を引き起こし、光学スピントルクはそれらのスピン、特に横方向の成分を誘発します。この動きは、共通の重心の周りを円軌道で移動する等しい質量の連星の動きに似ています。ガウスビームのウエストがターニングポイントよりも小さい場合、光学的に結合されたAuダイマーの軌道回転のヘリシティは入射CP光の利き手と反対になります。さらに、ガウスビームのウエストが減少すると、縦/横のSOCが重要になります。したがって、2つのNPの横方向のスピンはより深くなります。短距離相互作用の場合、光学力が相互作用を引き起こします。その結果、2つの結合したプラズモンNPは回転するだけでなく、らせん軌道で回転し、最終的に衝突します。さらに、2つの結合されたNPの長距離相互作用と短距離相互作用の間の粒子間距離の境界線は、おおよそ媒体の半波長にあります。私たちの結果は、光学力の大きさのオーダーが約pNであることを示しました。これは、他の力（たとえば、ポンデロモーティブ力）と比較して、NPの動きへの寄与を特定できます。私たちの発見は、ナノサイエンスとナノテクノロジーのための光操作NPへのSOCの応用への道を開くかもしれません。さらに、2つのNPの光学スピンと軌道トルクとEMフィールドのスピンと軌道の角運動量密度との相関関係を調べる価値があります。前者は\（\ operatorname {Im} \ left（\ overline {\ mathbf {E}} \ times \ mathbf {E} \ right）/ 2 \ omega \）で定義され、後者は参考文献に示されています。 [23]。さらに、メタマテリアルのねじれた近接場のSOCは調査する価値があります[40,41,42,43]。

略語

CP：

円偏光

EM：

電磁気

LH：

左利き

LP：

直線偏光

MMP：

多重極

MP：

微粒子

NP：

ナノ粒子

SOC：

スピン軌道相互作用