ナノリングベースのプラズモニックレンズの偏光依存準遠方場超集束戦略

背景

超解像イメージング[1]、粒子加速[2]、量子光学情報処理[3]、偏光依存光学データストレージ[4]の開発に伴い、表面プラズモンデバイスはこれらの領域でサブ波長の大きさのプラズモン共鳴。プラズモニックレンズ（PL）は、典型的なデバイスとして、2000年にJ. B. Pendryによって最初に提案された完全なイメージング機能を備えており[5]、サブ回折限界光学イメージングは​​X. Zhang etal。によって実験的に実証されました。 5年後[6]。ただし、エバネッセント波が指数関数的に減少するため、イメージング平面は非常に近いフィールドに限定され、発散する光フィールドを示します。この制限により、標準的な光学顕微鏡では実用的ではありません[7]。

近年、いくつかのナノ構造ベースのPLが調査されています[8、9、10、11、12、13、14、15、16、17、18、19、20、21、22、23、24]。これらのPLは、平面[8]または近接場[9]でのプラズモン集束を実現できるだけでなく、一般に走査型光学顕微鏡によって画像化された遠方場[10、11、12、13]での集束能力も備えています。顕微鏡[14]。しかし、これらのPLは、金属-絶縁体-金属（MIM）導波路の分散関係がナノスリットベースのPLに採用され、サブ波長スケールで位相を変調するまで、回折限界を超える集束を実現するのが非常に困難でした[11 、15、16、17]。正確な位相変調は、回折限界以下の焦点線に寄与し、直線偏光は通常、これらのレンズの入射光として適用されます。しかし、1次元ナノスリットレンズの同様の設計方法を2次元に拡張するだけでは、回転対称PLを直線偏光で照射した場合に円形の焦点を実現することはできず[18、19]、強い偏光依存性を示します。フォーカシング性能の。さらに、特にナノリングベースのPLの場合、焦点距離は波面再構成理論による数値計算から大幅に逸脱していました[18]。

回転対称性を備えたナノリングベースのPLは、以下の説明で簡単にするためにナノリングベースのプラズモンレンズ（NRPL）と呼ばれ、サブ波長集束システムの変換屈折レンズの代替として認識されています。しかし、表面プラズモンポラリトン（SPP）の励起の観点からは、励起効率は入射光のラジアル電界成分に比例するため、直線偏光はNRPLには適していません。比較すると、偏光が円筒対称の放射状偏光は、NRPLの構造特性に適応します[25]。さらに、ドーナツ型の開口絞り[26、27]またはフレネルゾーンプレート[28]を利用して、この偏光を適用して、サブ波長の円形の焦点を実現しました。したがって、放射状に偏光された光は、一般に、NRPLの入射光として適用されました[20、21、22、23]。空間フィルターを使用したサブ波長集束と比較して、これらのPLは、サブ波長導波路内の入射光の位相を変調する機能を備えています。表面プラズモン（SP）波の励起は、電磁波の伝達を強化することができます。ただし、遠方界でのプラズモンレンズの超集束能力は実証されていません。さらに、複合NRPLは焦点距離を変調することが提案されていますが[24]、焦点距離を効果的に制御することができず、電界エネルギーはレンズの端面の中央に集中しています。

本論文では、入射光の偏光特性を利用したスーパーフォーカシングの実現に重点を置いて、NRPLの理論設計と数値研究を紹介します。私たちの研究ではNRPLの理論的設計について説明し、有限差分時間領域（FDTD）数値シミュレーションに基づいて出力領域での集束性能を提供します。集束性能の偏光依存性を調査するために、線形、円形、方位角、および放射状に偏光された光がすべて照明のために考慮されます。サブ回折限界フォーカシング、焦点の形状、焦点距離の変調など、出力領域の電界分布の特徴について説明し、スーパーフォーカシング性能における同軸条件の重要性を指摘します。

メソッド

この研究で調査されたNRPLは、ナノスリットベースのPLに広く適用された波面再構成理論を使用して設計されました[11、15]。目的の位置に焦点を合わせるために、光が i を通過するときに発生する相対位相遅延 -個々のナノリングは、幾何光学に基づいて次の条件を満たす必要があります。

ここで、-Δ ϕ （ r _i ）は、内側の中心にある最初のナノリングと i の間の相対的な位相差です。 -番目のナノリング、 r は半径、λ ₀ は入射光の自由空間波長 n は任意の整数であり、 f ₀ は設計された焦点距離です。

調査対象のNRPLの基本的な構成要素は、金属膜にパターン化されたナノリングです。参考文献によると。 [29]、直径が入射光の波長よりも大きい場合、挿入図に示すように、金属壁に囲まれた空気ナノリングはMIM導波路モデルに近似できます。位相遅延は主に実数部によって定義されます。伝搬定数βの 、Re（βとして表される ）• t 、ここで t はナノリングの厚さです。分散関係に基づいて、複素伝播定数β 次のように計算できます：

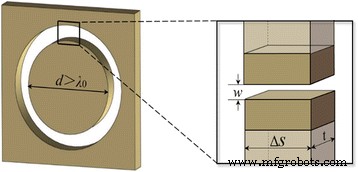
金膜に埋め込まれた個々のナノリングのMIM導波路モデル。 挿入図 ナノリングの任意の小さな部分の拡大図を示します

ここで k ₀ 真空中の波数ベクトルを表し、ε _d およびε _m それぞれ誘電体と金属の誘電率です。式に基づく（2）、伝播定数β ナノリングの幅に依存します。したがって、与えられた厚さのフラットレンズの場合 t 、発生する位相遅延は、幅 w によって簡単に決定されます。 光がそれを通過するときの個々のナノリングの。私たちの研究では、誘電体は誘電率εの空気に設定されています _d =1、厚さ t の金のフィルム 入射波長650nmでの誘電率がεである400nmの誘電率を採用しています。 _m =−12.8915 + 1.2044i [15]。さらに、以前に報告したように[16]、2つの隣接するMIM導波路内の伝搬光の結合効果も、特に間隔の金属壁が表皮深さの2倍よりも小さい場合に位相遅延に重要な役割を果たしますδ _m 、[30]で見積もることができます：

したがって、計算された表皮深さδ _m 約28nmです。結合効果を考慮することにより、0.38 λのスーパーフォーカス機能を備えたナノスリットベースのPL ₀ 解像度の低下は、以前の研究[16]で報告されました。ここでは、偏光状態（SOP）が集束性能に与える影響を顕著に分析するために、2つの隣接するナノリング間の間隔壁が2 δよりもはるかに大きい100nmになるように設計されています。 _m カップリング効果を排除します。

設計されたNRPLの概略図を図2に示します。波面を再構築するために、合計32個の同心ナノリングが含まれています。目的の位相変調範囲のナノリングの幅は10〜100nmです。狙った焦点距離 f ₀ は1300nm（2 λ ₀ ）。 MIM導波路モデルを効率的に利用するために、最も内側のナノリングの最小直径は800nmに設定されています。さらに、以前の研究[15]で説明したように焦点シフトを回避するために、合計位相差は10πと大きく、予測開口数（NA）は0.96です。その結果、0.61 λによって計算される理論的なレイリー回折限界 ₀ / NA [31]、は413 nm（〜0.64 λ ₀ 。

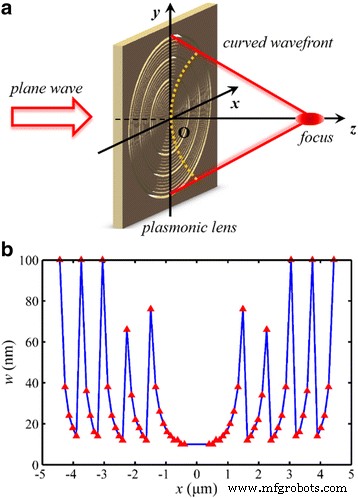
NRPLの概略図。 a 入射光は通常、レンズを照らします。 b レンズの構造パラメータ。 赤い三角形の座標値 半径 r を表します 幅 w 対応するナノリングの

空間強度分布、特に集束性能に対する入射光のSOPの影響を調査するために、設計されたNRPLは、それぞれ線形、円形、方位角、および放射状に偏光された光で照らされました。すべてのケースは、FDTD数値シミュレーションによって計算されました。マトリックス光学系によれば、さまざまな偏光はジョーンズマトリックス形式で記述でき、対応するマトリックス式を適用して入射光を定義します。モデルの境界は、レイヤー番号12の完全一致レイヤー（PML）でした。シミュレーションでの計算精度とメモリ消費のバランスをとるために、メッシュサイズは出力領域で10 nm、周囲で5nmに設定されました。焦点領域。

結果

I直線偏光

直線偏光の場合、SOPは空間的に均一であり、この場合、電気ベクトルの方向は x に平行です。 軸。光がNRPLを照らすとき、2つの焦点が存在し、全電界内で互いに400nm離れて分布します| E | ² 図3に示すように、両方の最大値の半分の全幅（FWHM）は210 nm（〜0.32 λ）ですが ₀ ）焦点面では、シミュレーション結果は、強度分布が、 z に正確に円形の焦点があるはずの波面再構成理論に基づく設計とは明らかに異なることを示しています。 軸（光軸とも呼ばれます）。

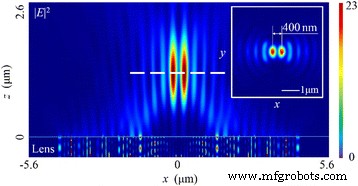
全電界の強度分布パターン| E | ² 直線偏光の入射光の場合。 挿入図 は焦点面の強度パターンを示しています。焦点距離は1215nm（偏差6.54％）です。両方の焦点のFWHMは〜0.32 λです ₀ 、互いに400 nm離れており、焦点深度（DOF）は〜1.68 λです。 ₀

シミュレーションと理論設計の違いを分析するために、電界成分の強度分布が調査されます。図4に示すように、 x-に楕円形の焦点とFWHMが表示されます。 および y- 方向は220nm（〜0.34 λ ₀ ）および457 nm（〜0.70 λ ₀ ）、 それぞれ。このパターンは、参考文献の実験結果とよく一致しています。 [18]同じ偏光が適用された場所。ただし、シミュレーションでは、| E の分布パターンが示されています。 | ² 縦方向のコンポーネントのパターンに似ています| E _z | ² これは総電気エネルギーの79.8％を占めています。したがって、この違いは主に| E の異常な分布に起因します。 _z | ² 。

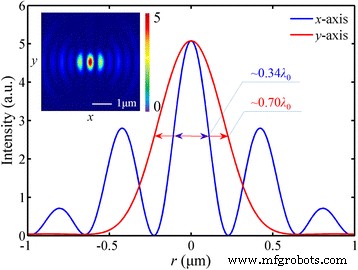
横成分の強度分布| E _r | ² 焦点面で。 挿入図 楕円形の焦点を示しています。焦点距離は1425nm（9.62％の偏差）です。 | E _r | ² 総電気エネルギーの20.2％を占めています。 DOFは〜1.41 λです ₀

この現象は、最終的にはNRPLの伝送特性によって説明できます。一方では、金属と誘電体の界面でのSPPの励起は、一般に、入射光の局所的な偏光方向に依存します。横波（TE）波は励起に寄与することができません。一方、MIM導波路のサブ波長構造により、SP波のみがこのレンズを伝搬できます[32]。レンズの回転対称性により、局所的な横磁気（TM）成分は方位角θで変化します。 コシノイドの形で。したがって、図5aに示すように、| E の強度分布 | ² レンズの端面のすぐ上にある、は y の近くに集中しています。 =0領域（−π / 4 <θ <π/ 4）。これに対応して、ポインティングベクトルは、図5bに示すように、端面の半径方向に沿って伝播します。したがって、 E のベクトル方向 基本的に光軸に平行であり、 E の主要なコンテンツを形成します _z 。対称的に建設的な干渉のため、円形タイプの焦点では​​なく、焦点面に2つの焦点が現れます。

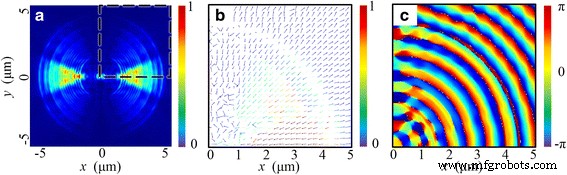
レンズの端面からわずか50nm上の断面における電界分布特性。 a | E の正規化された強度分布 | ² 。 b 破線内のポインティングベクトル分布 aの領域。 c E の対応する位相分布 _z

II円偏光

円偏光の状態は時間とともに周期的に変化するため、シミュレーション結果は時間平均された電界分布です。レンズがこの偏光で照らされると、| E にドーナツ型の焦点が形成されます。 _z | ² 。図6aに示すように、このフィールドの焦点距離は1185 nmであり、設計値に対して8.85％の偏差を示しています。ドーナツの幅は210nm（〜0.32 λ ₀ ）、半径は400nmです。焦点深度（DOF）は〜1.65 λです ₀ 。 | E の重み _z | ² 総電気エネルギーの80.6％です。さらに、| E _r | ² 、空間領域での重ね合わせにより、焦点距離1405 nm（偏差8.08％）の円形フォーカスが生成されます。 FWHMは295nm（〜0.45 λ ₀ ）このフィールドでは、DOFは〜1.68 λです。 ₀ 。さらに、 r-z の両方の分布パターン 平面は x のものに似ています - z 直線偏光の入射光の場合は平面。ラジアル電界成分を考慮することにより、FWHMを222 nm（〜0.34 λ）に減らすことができます。 ₀ 。

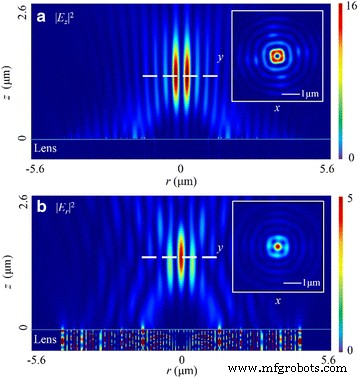
| E の強度分布パターン _z | ² および| E _r | ² r-z で 円偏光の場合は平面。 a | E _z | ² 、FWHM、DOF、および焦点距離は〜0.32 λです。 ₀ 、〜1.65 λ ₀ 、および1185 nm、それぞれ。 b | E _r | ² 、FWHM、DOF、および焦点距離は〜0.45 λです。 ₀ 、〜1.68 λ ₀ 、および1405 nm、それぞれ

III方位角偏光

方位角偏光の入射光の場合、電気ベクトルは半径方向に垂直であり、NRPLの金/真空界面に平行です。方位角偏光がレンズを照らすため、局所的なTE波は界面のSPPを励起できません。したがって、ナノリングの透過距離は、図7に示すように、それらの幅に比例します。構造と照明の両方が回転対称であるため、強度分布パターンとNRPLの構造の半分のみが示されています。透過光は無視でき、出力領域に明確な焦点はありません。

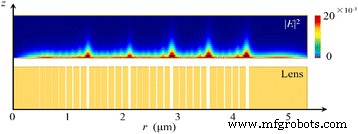
レンズ領域の強度分布パターンとその断面図。ナノリング内の非SP波の透過距離は、スリット幅に比例します

IV放射偏光

方位角偏光に対応して、放射状偏光は局所的なTM波と見なすことができ、この偏光特性はSPPの励起条件と一致し、焦点での最大強度が高くなります。総電界 E 、最大強度は直線偏光の入射光の5倍です。さらに、276 nm（〜0.42 λ）の円形の焦点があります。 ₀ ）| E のFWHM | ² 、図8に示すように、シミュレートされた強度分布は、高NA屈折レンズの集束能力に非​​常に似ています[33]。さらに、このフォーカシングパフォーマンスは依然として| E に依存しています _z | ² 、これは総電気エネルギーの82.0％を占めます。

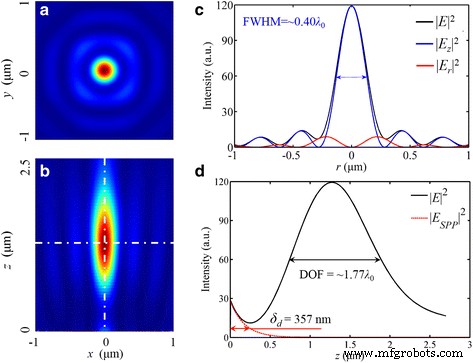
| E の強度分布 | ² 放射状に偏光した入射光の場合。 a 、 b 焦点面での分布と x での分布 - z 断面。 c 半径方向の強度プロファイル。 d 黒い実線が光軸に沿った強度プロファイル はシミュレーションにおける総電界強度分布と赤い破線です。 SPPの計算された曲線です。焦点距離は1275nm（1.92％の偏差）です。 | E のFWHM | ² および| E _z | ² は272nm（〜0.42 λ ₀ ）および260 nm（〜0.40 λ ₀ ）、 それぞれ。 DOFは〜1.77 λです ₀

前者の場合とは異なり、| E には円形の焦点があります _z | ² 。さらに、このコンポーネントは| E の分布パターンも決定します | ² 。図9aに示すように、| E のFWHM _z | ² は260nm（〜0.40 λ ₀ ）これは、ナノスリットベースのPLの場合の焦点線の焦点に近い[16]。特に焦点距離は1275nmです。設計値と比較すると、相対誤差は1.9％に減少します。ただし、| E の焦点距離は1455nm（偏差11.2％）です。 _r | ² 。図9bに示すように、幅227 nm（〜0.35 λ）のドーナツ型の焦点があります。 ₀ ） この分野で。 DOFは〜1.60 λです ₀ 。

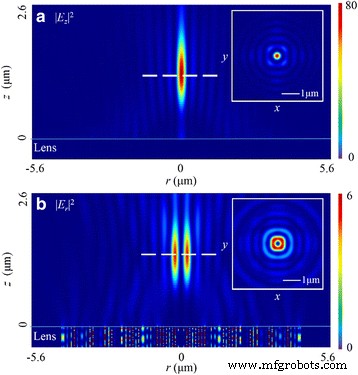
| E の強度分布パターン _z | ² および| E _r | ² r-z で 放射状に偏光した光の場合は平面。 a | E _z | ² r-z のパターン 飛行機。 挿入図 は、焦点面での円形の焦点を示しています。 b 横方向| E _r | ² r-z のパターン 飛行機。 挿入図 焦点面にドーナツ型の焦点を示しています

図10に示すように、ナノリング内のSP波の位相遅延が調査されます。シミュレーションは、位相変調がNRPLの構造パラメータによって劇的に影響を受け、入射面と出力面の間のシミュレートされた位相遅延が基本的に、式（1）に基づいて計算された値と同じです。 （2）。レンズの端面では、SP波は依然として半径方向に沿って伝播し、表面の中央にホットスポットがあり、その強度は焦点強度の5分の1です。回転対称分布を持つSP波の建設的な干渉は、伝播する波を構築し、準遠方場で円形の焦点を実現します。

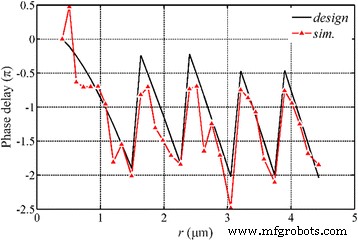
放射状に偏光された入射光の下でのNRPLの位相分析

ディスカッション

INRPLのスーパーフォーカス機能

線形偏光、円形偏光、放射状偏光など、さまざまなSOPの入射光が適用されるため、回折限界以下の焦点を実現できます。焦点形状はSOPの影響を受けますが、これらの焦点の特徴的なサイズはすべてレイリー回折限界（413 nm）を超えています。シミュレーション結果は、NRPLのスーパーフォーカス機能をうまく示しており、焦点面の強度分布は、非回折ビームを記述するために使用されるベッセル関数に似ています。

放射状に偏光した入射光の場合、図11に示す例のように、| E の強度分布 _z | ² ゼロ次ベッセル関数 J と同じです ₀ （ K _spp ⋅ n ⋅ r ）、ここで n および r は、それぞれ環境媒体の屈折率と光軸までの半径方向の距離です。フォーカスのFWHMは、 J で計算されたメインローブのサイズよりもわずかに大きくなっています。 ₀ 。特に、シミュレーションは、非回折ビームが準遠方場で実現できることを示しています。エバネッセント波の一種であるSP波は、出口面から離れる方向に伝播すると指数関数的に減少し、真空中の伝播距離は[30]：

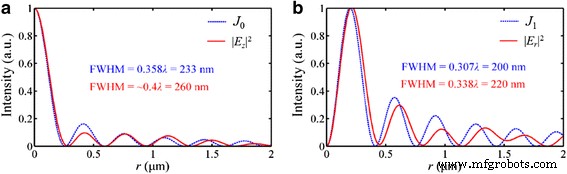
放射状に偏光された入射光の下での焦点面におけるNRPLの強度プロファイル。 a | E の分布 _z | ² ゼロ次ベッセル関数 J に似ています ₀ 。 b | E の分布 _r | ² 一次ベッセル関数 J に似ています ₁

ここで、ε _d およびε _m それぞれ誘電体と金属の誘電率です。したがって、δ _d は357nmであり、図8dに示すシミュレーションと一致しています。したがって、焦点でのSP波の強度は、準遠方界領域では無視できます。

IIフォーカスの形

SOPを変調することにより、図12に示すように、焦点面で楕円形、円形、ドーナツ型の焦点を実現できます。この現象はサブ波長の焦点サイズに起因し、円形タイプは実現できません。同時に電場と磁場の両方に焦点を合わせます。したがって、ドーナツタイプの焦点は磁場（または電場）で実現され、円形タイプの焦点は対応する電場（または磁場）で達成されます。特に、縦磁場がないため、| H の強度分布 | ² | E のパターンと同じです _r | ² 。さらに、| E _z | ² 総電気エネルギーの約80.0％を占め、スケールは入射光のSOPの影響を受けません。

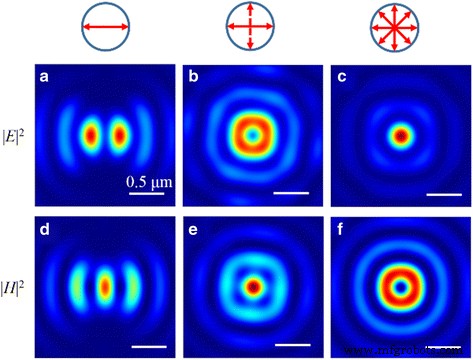
電界の正規化された強度パターン| E | ² と磁場| H | ² NRPLが偏光によって照らされたときの焦点面で。 a | E | ² および d | H | ² 直線偏光の入射光による分布。 b | E | ² および e | H | ² 円偏光の入射光による分布。 c | E | ² および f | H | ² 放射状に偏光した入射光による分布

III焦点距離の変調

さまざまなケースでシミュレートされた焦点距離は、基本的に目的の位置 f に近いです。 ₀ （1300 nm）、表1に示すように、しかし、横方向のフィールドの焦点距離| E _r | ² 縦方向のフィールドよりも約200nm長い| E _z | ² 、入射光のSOPに関係なく、偏差は一般的に存在します。

理論的には、波面再構成理論は、近距離場から遠距離場までの任意の焦点距離でNRPLを設計するのに適しています。ただし、設計されたプラズモニックレンズの実際の焦点距離が設計された焦点距離とよく一致するかどうかは、レンズの合計位相差に依存します。偏差は、振幅タイプのフォーカスと位相タイプのフォーカスの違いに起因する可能性があります[34]。 MIM導波路の位相変調は放射状成分を対象としているため、| E の焦点距離 _r | ² 少なくとも2πの全位相差が満たされる場合、波面再構成理論によって変調することができます[15]。縦方向の成分の場合、より大きな総位相差（>10π）が一貫性に有利です。図13に示すように、位相差が2πから16πに増加すると、それに対応してNAが0.75から0.96になり、| E の振幅タイプの焦点が変化します。 _z | ² レンズの出力面から希望の位置に移動します。 | E の強度分布として | ² | E によって決定されます _z | ² 、NAは全電界の焦点距離に劇的に影響を与える可能性があります。ただし、| E での焦点距離の変化 _z | ² 総位相差の増加とともに、徐々に減少します。一方、| E の位相型フォーカスの位置 _r | ² 比較的安定しています。 NAの高いNRPLを適用した場合でも、| E の強度分布に基づいて導出された焦点距離には偏差があります。 _x | ² および| E _z | ² 、および偏差はほとんど不変に保たれます。したがって、NRPLの焦点距離は、位相変調と構造最適化によって効果的に制御できますが、横方向と縦方向の成分フィールドで同じ焦点距離を達成することはできません。

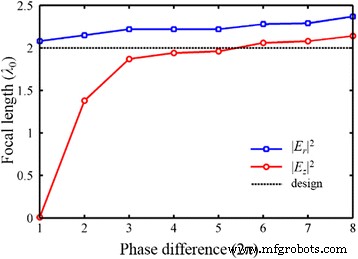
総位相差が2πから16πに増加した場合のNRPLの焦点距離

IV非同軸状況でのパフォーマンスのフォーカシング

非同軸状態は実験で一般的な問題であり、集束性能への影響を考慮する必要があります。図14に示すように、放射状に偏光した光の中心は、 x に沿ってNRPLの光軸から3μmずれています。 軸。イチジクと比較して。図8および9では、 x-z の両方の強度分布 断面と焦点面が明らかに変化しています。縦電界では、楕円形の焦点がレンズの出口面から1340nm離れたところにあります。 x-z のFWHM および y-z 平面は0.51と0.38 λです ₀ 、 それぞれ。一方、横電界の分布も歪んでおり、一方のサイドローブの強度がもう一方のサイドローブよりも高くなっています。さらに、同軸条件と比較して、全電界の最大強度の減少は85％以上です。

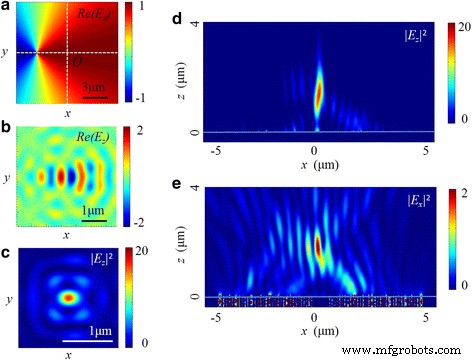
非同軸状態でのNRPLの強度分布。 a E の実数 _x 放射状に偏光された入射光の。 b 、 c Re（E の分布 _z ） および| E _z | ² 焦点面で。 d 、 e | E の分布 _z | ² および| E _x | ² x-z で 平面

予備シミュレーションは、非同軸状態が実際にレンズの強度分布と望ましい集束性能に影響を与えることを示しています。したがって、実験中は入射光とレンズ中心の間の同軸性を保証することが不可欠です。

結論

要約すると、波面再構成理論とMIM導波路の分散関係を利用して、高NAのNRPLを構築します。また、焦点距離、FWHM、DOF、最大強度など、準遠方場での偏光依存の集束性能についても調査します。線形、円形、放射状、および方位角方向に偏光された光などの従来の偏光がすべて考慮されます。シミュレーションは、設計されたNRPLのスーパーフォーカス機能を示しています。偏光依存特性を利用して、サブ回折限界の楕円形、円形、およびドーナツ形の焦点を実現することができます。ただし、この作業の1つの制限は、NRPLのスーパーフォーカシング性能を実現するために提案された設計戦略が準​​遠方界領域を対象としていることです。ただし、私たちの知る限り、この領域での同様のフォーカシング機能はほとんど報告されていません。さらに、焦点シフトの根本的な物理現象を発見し、横方向と縦方向の両方のフィールドを使用して、焦点位置を制御するためのより効果的な方法を提案します。超解像イメージング、粒子加速、量子光学情報処理から光学データストレージに至るまで、ナノリングベースのスーパーフォーカシングレンズにはかなりのエンジニアリングアプリケーションがあります。

略語

DOF：

焦点深度

FDTD：

有限差分時間領域

FWHM：

半値全幅

MIM：

金属-絶縁体-金属

NRPL：

ナノリングベースのプラズモンレンズ

PML：

完全一致レイヤー

SOP：

分極状態

SPP：

表面プラズモンポラリトン

TE：

横電気

TM：

横磁気