カーボンナノチューブベースのナノワイヤ共振器の電気機械的振動における幾何学的相の特性
要約
幾何学的位相は、振動の波動関数における追加の位相進化であり、幅広い科学技術に適用できる可能性があります。カーボンナノチューブベースのナノワイヤ共振器のスクイーズド状態での幾何学的位相の特性は、不変演算子法によって調査されました。複雑な時間依存ハミルトン系の処理に役立つ線形不変演算子の導入により、幾何学的位相の解析式を導き出すことができました。これを利用して、関連する図に基づいて幾何学的位相の時間的振る舞いを分析しました。幾何学的位相の進展に対する圧搾パラメータの影響が調査された。幾何学的位相は大きく振動し、そのような振動の包絡線は時間とともに増加します。振動の古典的な振幅、減衰係数、駆動力の振幅などのパラメーターが大きい場合、幾何学的位相の増加率は大きくなります。システムの角周波数が共振角周波数の近くに達した場合、時間の経過とともに幾何学的位相が非常に急激に増加することを確認しました。幾何学的位相の特性に関する私たちの開発は、ナノワイヤ振動の位相的特徴を理解するために重要です。
はじめに
カーボンナノチューブベース(CNTベース)のナノワイヤー[1–3]、半導体ナノワイヤー[4]、グラフェン[5]、浮遊粒子[6]などの最小の共振器の機械的振動が主な研究テーマとなっています。ナノサイエンスコミュニティで10年以上。外部周期力によって駆動されるナノワイヤ共振器の電気機械振動に関する活発な研究が、理論的および実験的領域の両方で行われてきました。特に、CNTベースのナノワイヤ共振器は、周囲からの小さな摂動に対する高品質の要因による並外れた感度により、ナノスケールの機械的デバイスとしてかなりの関心を集めています。浮遊CNTベースのナノワイヤ共振器は、EM波[2]、小さな力[7]、質量[8]、温度[9]、ノイズ[10]などの幅広い物理量を測定する装置の有望な候補です。
システムの根底にある特徴を理論的に解明するには、ナノワイヤ振動における量子相進化の分析が必要です。 CNTベースのナノワイヤ共振器の量子振動状態[11]に関しては、幾何学的位相[12]と通常の動的位相が、位相の補足的な進化として現れます。幾何学的位相[12]は、物理学のさまざまな分野に適用できる量子状態の非ホロノミックです。幾何学的位相の分析は、共鳴プロファイル[13、14]、強い量子振動[15、16]、ひずみ緩和メカニズム[17、18]、ディラック磁気プラズモンの出現など、ナノワイヤーのナノ特性を特徴づけるのに潜在的に採用できます。 [19]、およびアハラノフ-ボーム振動のトポロジー[20]。
非断熱ダイナミクスに関連する幾何学的位相の研究は、正確なシミュレーション技術の進歩に必要なナノメカニカルシステムの洞察を提供する可能性があります[21]。量子状態の準備、操作、および検出は、量子技術の重要な要素です。本研究の目的は、ナノワイヤ振動の量子状態で起こる幾何学的位相の時間的振る舞いに光を当てることです。 CNTベースのナノワイヤ振動のメカニズムを理解するために、コヒーレント状態のような古典的な量子状態であるスクイーズド状態での幾何学的位相の時間発展を調査します。スクイーズド状態のメリットは、コヒーレント状態ではこのような不確実性変調が不可能であるのに対し、その状態での求積法の不確実性は、他の求積法の不確実性を高めることを犠牲にして大幅に減らすことができることです。特に、幾何学的位相に対する共振の影響を分析します。共鳴エネルギーは非共鳴状態のエネルギーとは大きく異なるため[22、23]、波動関数の位相的振る舞いは自明ではなく、通常の状況での振る舞いからかなり逸脱する可能性があります。物理的パラメータの変更と絞りパラメータが幾何学的位相の変化に与える影響も厳密に分析されます。幾何学的位相は動的システム[24]に遍在し、量子計算[25]、強度干渉計[26]、フォトニックマルチタスク[27]、量子センシングプロトコル[28]、波などのさまざまな最新技術に適用できます。 -安定性の測定[29]。
システムのハミルトニアンには、システムの減衰と外部駆動力に関連する時間関数が含まれます。したがって、このシステムは一種の時間依存ハミルトン系(TDHS)であり、その量子力学的問題は最近まで広く研究されています。 TDHSのハミルトニアンの時間関数は、ほとんどの場合、正規変数の関数から分離できないため、シュレディンガー方程式を解くための従来の変数分離法は利用できません。この困難を克服するために開発された代替の強力な方法は、ルイスとリーゼンフェルドによって導入された不変演算子法です[30、31]。この方法は、TDHSの量子解を導出するときに非常に便利な数学的ツールです。 TDHSによって記述される多くの量子力学的問題はこの方法に基づいて調査されます。たとえば、それらには、カオス的粒子散乱[32]、時変媒体での光伝搬[33]、トラップされた駆動電子の制御[34]、および量子ナノ電子回路の非古典性[35]が含まれます。 TDHSの量子力学的処理には、ユニタリ変換法[36]、リー代数法[37]、ハミルトニアン推定法[38]など、さまざまな方法があります。
システムがTDHSであるということに関して、システムの量子解を得るために不変演算子法を使用します。消滅演算子で表される線形不変演算子を紹介します。システムの時間依存性により、消滅演算子と生成演算子は時間で表されますが、これらのラダー演算子を使用すると、コヒーレント状態とスクイーズド状態の両方を取得できます。システムの幾何学的位相は、スクイーズド状態の波動関数を利用して解析的に評価されます。幾何学的位相の時間発展は、パラメーターの多様な選択で描かれたその図に基づいて詳細に分析されます。
メソッド
幾何学的位相を調査するには、最初にナノワイヤ先端の古典的な運動方程式を設定する必要があります。 TDHSの量子波の進化には幾何学的位相が現れるため、私たちが管理する特定の量子状態で波動関数を導出する必要があります。導入部で述べたように、スクイーズド状態を検討します。スクイーズド状態を含む、TDHSの多様な量子状態での波動関数は、不変演算子法から取得できます。
時間依存振幅 x の運動方程式 有効質量 m の浮遊カーボンナノチューブの曲げモードの場合 [1]によって与えられます
$$ \ ddot {x} + \ left(\ frac {\ omega_ {0}} {Q} + \ eta x ^ {2} \ right)\ dot {x} + \ left(\ omega_ {0} ^ { 2} + \ beta x ^ {2} \ right)x =f _ {\ mathrm {d}} \ cos(\ omega t)、$$(1)ここでω 0 は共振角周波数、 Q 品質係数、 f d 静電駆動力を m で割った値 、η 非線形減衰係数、およびβ Duffingパラメータ。便宜上、先端の変位がCNTワイヤの長さに比べて十分に小さいと仮定します。次に、式(1)の非線形項を無視できます。 (1)、[2]につながる
$$ \ ddot {x} + \ frac {\ omega_ {0}} {Q} \ dot {x} + \ omega_ {0} ^ {2} x =f _ {\ mathrm {d}} \ cos(\ omega t)。 $$(2)式を生成するシステムのハミルトニアン。 (2)は
によって与えられます $$ \ hat {H} =e ^ {-\ gamma t} \ frac {\ hat {p} ^ {2}} {2m} + \ frac {1} {2} me ^ {\ gamma t} \ left [\ omega_ {0} ^ {2} \ hat {x} ^ {2} -2f _ {\ mathrm {d}} \ cos(\ omega t)\ hat {x} \ right]、$$(3)ここで、γ =ω 0 / Q 。式の古典的な解。 (2)は補完関数 X で構成されています c ( t )および特定のソリューション X p ( t )、
によって与えられます $$ \ begin {array} {@ {} rcl @ {}} &&X_ {c}(t)=X_ {c、0} e ^ {-\ gamma t / 2} \ cos(\ Omega t + \ varphi) 、\ end {array} $$(4)$$ \ begin {array} {@ {} rcl @ {}} &&X_ {p}(t)=X_ {p、0} \ cos(\ omega t- \ delta)、\ end {array} $$(5)ここで X c 、0 は定数、\(\ Omega =\ sqrt {\ omega _ {0} ^ {2}-\ gamma ^ {2} / 4} \)、φ は任意のフェーズであり、
$$ \ begin {array} {@ {} rcl @ {}} X_ {p、0}&=&\ frac {f _ {\ mathrm {d}}} {\ sqrt {\ left(\ omega_ {0} ^ {2}-\ omega ^ {2} \ right)^ {2} + \ gamma ^ {2} \ omega ^ {2}}}、\ end {array} $$(6)$$ \ begin {array} {@ {} rcl @ {}} \ delta&=&\ tan ^ {-1} \ frac {\ gamma \ omega} {\ omega_ {0} ^ {2}-\ omega ^ {2}}。 \ end {array} $$(7)運動量空間の古典的な解は同様の方法で与えられ、相補関数は\(P_ {c}(t)=me ^ {\ gamma t} \ dot {X} _ {c}(t)\)です。特定の解は\(P_ {p}(t)=me ^ {\ gamma t} \ dot {X} _ {p}(t)\)です。システムの幾何学的位相を調査するには、最初に量子解を導出する必要があります。式で与えられたシステムのハミルトニアンに注意してください。 (3)は明示的に時間に依存します。システムの量子解を導出するために、不変演算子法[30、31]を使用します。これは、このような時変システムを扱うときに役立つ方法です。システムの不変演算子\(\ hat {I} \)は、\({d \ hat {I}} / {dt} ={\ partial \ hat)で与えられるLiouville-vonNeumann方程式から導出できます。 {I}} / {\ partial t} + \ left [\ hat {I}、\ hat {H} \ right] / \ left(i \ hbar \ right)=0 \)。したがって、式を挿入した後の厳密な評価から。 (3)この方程式には、
の形式の線形不変演算子[34]があります。 $$ \ hat {I} =\ hat {A} e ^ {i \ Omega t}、$$(8)ここで、\(\ hat {A} \)は、
によって与えられる消滅演算子です。 $$ \ begin {aligned} \ hat {A} =&\ left(2 \ hbar m \ Omega \ right)^ {-1/2} \ left [m \ left(\ Omega + i \ frac {\ gamma} { 2} \ right)e ^ {\ gamma t / 2} \ left [\ hat {x} -X_ {p}(t)\ right] \ right。\\&\ left。+ ie ^ {-\ gamma t / 2} \ left [\ hat {p} -P_ {p}(t)\ right] \! {\ vphantom {\ left(\ Omega + i \ frac {\ gamma} {2} \ right)}} \ right]。 \ end {aligned} $$(9)式のエルミート随伴。 (9)、\(\ hat {A} ^ {\ dagger} \)は、生成演算子です。
\(\ hat {A} \)の固有値方程式を
と表すことができます。 $$ \ hat {A} | A \ rangle =A | A \ rangle。 $$(10)上記の式を評価することにより、
のような固有値の式が得られます。 $$ A(t)=A(0)e ^ {-i \ Omega t}、$$(11)ここで A (0)= A 0 e − i φ
$$ A_ {0} =\ left [m \ Omega /(2 \ hbar)\ right] ^ {1/2} X_ {c、0}。 $$(12)コヒーレント状態の間| A 〉は\(\ hat {A} \)の固有状態であり、スクイーズド状態は
によって与えられる演算子\(\ hat {B} \)の固有状態です。 $$ \ hat {B} =\ mu \ hat {A} + \ nu \ hat {A} ^ {\ dagger}、$$(13)ここでμ およびν 方程式を生成する複素変数です
$$ | \ mu | ^ {2}-| \ nu | ^ {2} =1。 $$(14)\(\ hat {B} \)の固有値方程式を
の形式で書くと $$ \ hat {B} | B \ rangle =B | B \ rangle、$$(15)| B 〉はスクイーズド状態です。構成空間でこの方程式を解くことにより、
が得られます。 $$ {\ begin {aligned} \ langle {x} | B \ rangle =&^ {4} \!\!\!\ sqrt {\ frac {m \ Omega e ^ {\ gamma t}} {\ hbar \ pi(\ mu- \ nu)(\ mu ^ {*}-\ nu ^ {*})}} \ exp \ left \ {-\ frac {1} {\ hbar(\ mu- \ nu)} \ left [\ frac {1} {2} me ^ {\ gamma t} \ left({\ vphantom {\ frac {1} {2}}}(\ mu + \ nu)\ Omega \ right。\ right。\ right。 \\&\ left。+ \ frac {i \ gamma} {2}(\ mu- \ nu)\ right)\ left [x-X_ {p}(t)\ right] ^ {2}-[iP_ { p}(t)(\ mu- \ nu)+ \ left(2 \ hbar m \ Omega e ^ {\ gamma t} \ right)^ {1/2} \\&\ left。 \ left。\ times(\ mu A + \ nu A ^ {*})] \ left [x-X_ {p}(t)\ right] {\ vphantom {\ frac {1} {2} me ^ {\ gamma t}}} \ right]-\ frac {| A | ^ {2} + A ^ {2}} {2(\ mu- \ nu)(\ mu ^ {*}-\ nu ^ {*})} \正しい\}。 \ end {aligned}} $$(16)このように、スクイーズド状態の波動関数は、式(1)で与えられるように導出されています。 (16)。このような波動関数の分析的記述に基づいて、システムの量子的特徴を明らかにすることができます。 μの場合 =1およびν =0、式(16)は、コヒーレント状態の波動関数に還元されます。これは、式(16)の固有状態です。 (10)構成スペース。波動関数、式。 (16)は、スクイーズド状態の幾何学的位相を導出するために、次のセクションで使用されます。
結果と考察
量子波の進化の位相には、動的位相だけでなく幾何学的位相も含まれることはよく知られています。幾何学的位相は、断熱変化を伴って周期的に進化するシステムについて、1984年にベリーによって最初に発見されました[12]。量子力学の断熱定理によれば、パラメータ空間での周期的進化における量子状態の瞬間的な固有状態は、後で同じ状態のままになりますが、ベリー相である量子相の追加の蓄積があります。量子系の非断熱的、非周期的、および/または非単一進化を含む方法でのベリー位相の一般化は、幾何学的位相です。
スクイーズド状態の幾何学的位相は
で与えられます。 $$ \ gamma_ {G}(t)=\ int_ {0} ^ {t} \ langle B(t ')| i \ frac {\ partial} {\ partial t'} | B(t ')\ rangle dt' + \ gamma_ {G}(0)。 $$(17)配位空間における時間に対する波動関数の微分は
になります。 $$ \ frac {\ partial \ langle {x} | B \ rangle} {\ partial t} \、=\、\ left \ {f_ {1}(t)\!\ left [x-X_ {p}( t)\ right] ^ {2} \、+ \、f_ {2}(t)\ left [x \、-\、X_ {p}(t)\ right] \、+ \、f_ {3}( t)\ right \} \! \!\ langle {x} | B \ rangle、$$(18)ここで
$$ f_ {1}(t)=-\ frac {m \ gamma e ^ {\ gamma t}} {2 \ hbar(\ mu- \ nu)} \ left((\ mu + \ nu)\ Omega + \ frac {i \ gamma} {2}(\ mu- \ nu)\ right)、$$(19)$$ {\ begin {aligned} f_ {2}(t)&=\ frac {1} {\ hbar (\ mu- \ nu)} \ left [\ left((\ mu + \ nu)\ Omega + \ frac {i \ gamma} {2}(\ mu- \ nu)\ right)P_ {p}(t) -ime ^ {\ gamma t} \ right。\\&\ quad \ times \ left [\ omega_ {0} ^ {2} X_ {p}(t)-f _ {\ mathrm {d}} \ cos(\ omega t)\ right](\ mu- \ nu)+ \ left(2 \ hbar m \ Omega e ^ {\ gamma t} \ right)^ {1/2} \\&\ quad \ left。\ times \ left(\ frac {\ gamma} {2} \ left(\ mu A + \ nu A ^ {*} \ right)-i \ Omega \ left(\ mu A- \ nu A ^ {*} \ right)\ right)\ right]、\\ \ end {aligned}} $$(20)$$ {\ begin {aligned} f_ {3}(t)&\!=\ frac {\ gamma} {4}-\ frac {1} {\ hbar me ^ {\ gamma t}(\ mu- \ nu)} \ left [iP_ {p}(t)(\ mu- \ nu)+ \ left(2 \ hbar m \ Omega e ^ {\ gamma t} \ right)^ {1/2} \ right。\\&\ quad \ left。\ times \ left(\ mu A + \ nu A ^ {*} \ right){\ vphantom {\ left( 2 \ hbar m \ Omega e ^ {\ gamma t} \ right)^ {1/2}}} \ right] P_ {p}(t)+ \ frac {i \ Omega A ^ {2}} {(\ mu- \ nu)\ left(\ mu ^ {*}-\ nu ^ {*} \ right)}。 \ end {aligned}} $$(21)式を挿入した後のさらなる評価。 (18)式に(17)与える
$$ {\ begin {aligned} \ gamma_ {G}(t)=&\ int_ {0} ^ {t} dt '\ left [A_ {0} ^ {2} \ left(\ frac {\ gamma ^ { 2}} {4 \ Omega} + \ Omega + g_ {1} \ sin \ left [2 \ left(\ Omega t '+ \ varphi \ right)\ right] + g_ {2} \ cos \ left [2 \ left(\ Omega t '+ \ varphi \ right)\ right] \ right)\ right。\\&\ left.-A_ {0} \ left [g_ {3}(t')\ sin \ left(\ Omega t '+ \ varphi \ right)+ g_ {4}(t')\ cos \ left(\ Omega t '+ \ varphi \ right)\ right] + g_ {5}(t'){\ vphantom {\ frac {\ gamma ^ {2}} {4 \ Omega}}} \ right] + \ gamma_ {G}(0)、\ end {aligned}} $$(22)ここで
$$ \ begin {array} {* {20} l} g_ {1}〜&=\ frac {\ gamma} {2} + \ frac {i \ Omega \ left(\ mu \ nu ^ {*}-\ mu ^ {*} \ nu \ right)} {(\ mu- \ nu)\ left(\ mu ^ {*}-\ nu ^ {*} \ right)}、\ end {array} $$(23) $$ \ begin {array} {* {20} l} g_ {2}〜&=\ frac {\ gamma ^ {2}} {4 \ Omega} + \ Omega \ frac {2 | \ nu | ^ {2 }-\ left(\ mu \ nu ^ {*} + \ mu ^ {*} \ nu \ right)} {(\ mu- \ nu)\ left(\ mu ^ {*}-\ nu ^ {*} \ right)}、\ end {array} $$(24)$$ \ begin {array} {* {20} l} g_ {3}(t)&=\ left(\ frac {2 \ Omega} {m \ hbar e ^ {\ gamma t}} \ right)^ {1/2} P_ {p}(t)、\ end {array} $$(25)$$ {\ begin {aligned} g_ {4}( t)=\ frac {1} {\ sqrt {2 \ hbar \ Omega}} \ left(\ frac {\ gamma} {\ sqrt {me ^ {\ gamma t}}} P_ {p}(t)-2 \ sqrt {me ^ {\ gamma t}} \ left [\ omega_ {0} ^ {2} X_ {p}(t)-f _ {\ mathrm {d}} \ cos(\ omega t)\ right] \右)、\ end {aligned}} $$(26)$$ {\ begin {aligned} g_ {5}(t)&=\ frac {P_ {p} ^ {2}(t)} {\ hbar me ^ {\ gamma t}} + \ frac {\ gamma ^ {2}} {8 \ Omega} \ left [2 | \ nu | ^ {2}-\ left( \ mu \ nu + \ mu ^ {*} \ nu ^ {*} \ right)+1 \ right] \\&\ quad + \ frac {i \ gamma} {4(\ mu- \ nu)\ left(\ mu ^ {*}-\ nu ^ {*} \ right)} \ left [| \ mu | ^ {2} \ left(\ nu ^ {2}-\ nu ^ {* 2} \ right)-| \ nu | ^ {2} \ left(\ mu ^ {2}-\ mu ^ {* 2} \ right)\ right。\\&\ quad \ left。+(2 | \ nu | ^ {2} + 1 )\ left(\ mu \ nu ^ {*}-\ mu ^ {*} \ nu \ right)+(\ mu- \ mu ^ {*})(\ nu- \ nu ^ {*})\ right] 。 \ end {aligned}} $$(27)g の最後の用語 5 (μを含む − μ ∗ )(ν − ν ∗ )は純粋に虚数であるため、フェーズとしては不十分です。したがって、μの少なくとも1つを選択して、この用語を削除します。 およびν 実際の値として。 μ間の相対位相のみであるため、この救済策は一般性を失うことなく常に実行できます。 およびν 絶対的な位相ではなく、物理的な意味があります。
式の積分の実行から。 (22)、
$$ {\ begin {aligned} \ gamma_ {G}(t)&=A_ {0} ^ {2} \ left [\ left(\ frac {\ gamma ^ {2}} {4 \ Omega} + \ Omega \ right)t + \ frac {g_ {1}} {\ Omega} \ sin(\ Omega t + 2 \ varphi)\ sin(\ Omega t)+ \ frac {g_ {2}} {\ Omega} \ cos (\ Omega t + 2 \ varphi)\ right。\\&\ quad \ left。\ times \ sin(\ Omega t){\ vphantom {\ frac {\ gamma ^ {2}} {4 \ Omega}}} \ right] \!-A_ {0} \ left [\ left(\ frac {2m \ Omega} {\ hbar} \ right)^ {1/2} \ omega X_ {p、0} \ bar {g} _ {3}(t)+ \ sqrt {\ frac {2m} {\ hbar \ Omega}} \ frac {1} {4 \ omega ^ {2} + \ gamma ^ {2}} \ bar {g} _ { 4}(t)\ right] \\&\ quad + \ bar {g} _ {5}(t)+ \ gamma_ {G}(0)、\ end {aligned}} $$(28)ここで、\(\ bar {g} _ {i}(t)〜(i =3,4,5)\)は
で与えられます $$ \ bar {g} _ {i}(t)=G_ {i}(t)-G_ {i}(0)、$$(29)$$ {\ begin {aligned} G_ {3}(\ tau)&=e ^ {\ gamma \ tau / 2} \ left(\ frac {1} {4(\ Omega + \ omega)^ {2} + \ gamma ^ {2}} \ left \ {2(\ Omega + \ omega)\ sin [(\ Omega + \ omega)\ tau + \ varphi- \ delta] \ right。\ right。\\&\ quad \ left。+ \ gamma \ cos [(\ Omega + \ omega)\ tau + \ varphi- \ delta] \ right \}-\ frac {1} {4(\ Omega- \ omega)^ {2} + \ gamma ^ {2}} \ {2(\ Omega- \ omega)\\&\ quad \ left。\ left。\ times \ sin [(\ Omega- \ omega)\ tau \、+ \、\ varphi \、+ \、\ delta] \ !+ \ gamma \ cos [(\ Omega- \ omega)\ tau \、+ \、\ varphi \、+ \、\ delta] \ right \} {\ vphantom {\ frac {1} {4(\ Omega + \ omega)^ {2} + \ gamma ^ {2}}}} \ right)、\\ \ end {aligned}} $$(30)$$ {\ begin {aligned} G_ {4}(\ tau)& =e ^ {\ gamma \ tau / 2} \ left \ {X_ {p、0} \ left \ {\ gamma \ omega [2 \ omega \ cos(\ omega \ tau- \ delta)-\ gamma \ sin( \ omega \ tau- \ delta)] -2 \ omega_ {0} ^ {2} \ right。\ right。\\&\ quad \ left。\ times [2 \ omega \ sin(\ omega \ tau- \ delta )+ \ gamma \ cos(\ omega \ tau- \ delta)] {\ vphantom {X_ {p、0}}} \ right \} + 2f _ {\ mathrm {d}} [2 \ omega \ sin(\ omega \ tau)\\&\ left。\ left。\ quad + \ gamma \ cos(\ omega \ tau)\ right] {\ vphantom {X_ {p、0}}} \ right \}、\\ \ end {aligned}} $$(31)$$ {\ begin {aligned} G_ {5}(\ tau)&=\ frac {m \ omega ^ {2}} {2 \ hbar} X_ {p、0} ^ {2} \ frac {e ^ {\ gamma \ tau}} {\ gamma \ left(4 \ omega ^ {2} + \ gamma ^ {2} \ right)} \ left \ {\ gamma ^ {2} + 4 \ omega ^ {2}-\ gamma ^ {2} \ cos [2(\ omega \ tau- \ delta)] \ right。 \\&\ quad \ left.-2 \ gamma \ omega \ sin [2(\ omega \ tau- \ delta)] {\ vphantom {\ gamma ^ {2} + 4 \ omega ^ {2}-\ gamma ^ {2}}} \ right \} + \ frac {\ gamma ^ {2} \ tau} {8 \ Omega} \ left [2 | \ nu | ^ {2}-\ left(\ mu \ nu + \ mu ^ {*} \ nu ^ {*} \ right)+1 \ right] \\&\ quad + \ frac {i \ gamma \ tau} {4(\ mu- \ nu)\ left(\ mu ^ {*}- \ nu ^ {*} \ right)} \ left [| \ mu | ^ {2} \ left(\ nu ^ {2}-\ nu ^ {* 2} \ right)-| \ nu | ^ {2} \ left(\ mu ^ {2}-\ mu ^ {* 2} \ right)\ right。\\&\ quad \ left。+ \ left(2 | \ nu | ^ {2} + 1 \ right)\ left(\ mu \ nu ^ {*}-\ mu ^ {*} \ nu \ right)\ right]。 \ end {aligned}} $$(32)
したがって、スクイーズド状態での完全な幾何学的位相を評価しました。これは、式(1)で与えられます。 (28)式(23)、(24)、および(29)–(32)。
幾何学的位相の時間発展は、図1および2に示されています。 1、2、3、および4。図1から、幾何学的位相が振動し、そのような振動の包絡線が時間の経過とともに増加することがわかります。 A の場合、エンベロープの増加は大きくなります。 0 は大きい。 μの値に応じて、振動のパターンは徐々に不規則になります。 およびν 増加。また、時間の経過とともに振動の振幅が大きくなります。
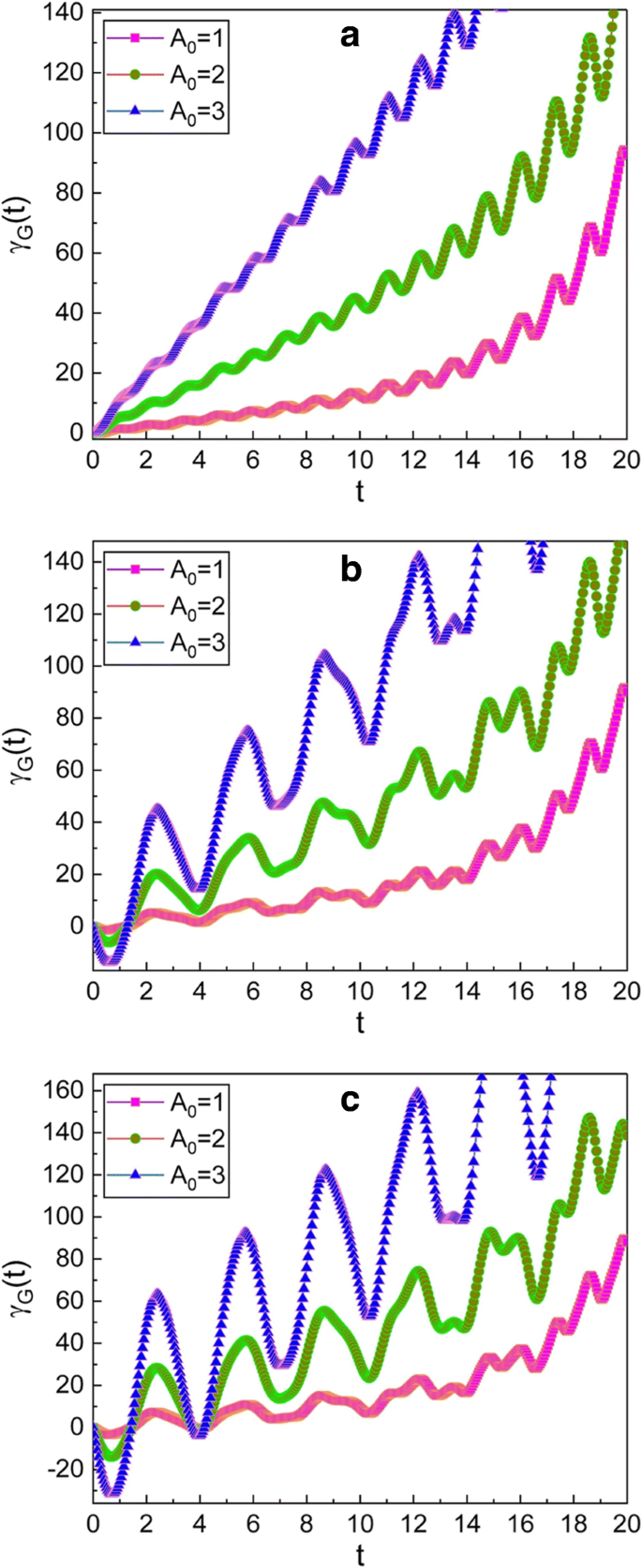
A のいくつかの異なる値に対する幾何学的位相の時間発展 0 。 (μの値 、ν グラフィックで使用されている)は、 a の場合は(1、0)です。 、(\(\ sqrt {2} \)、1)for b 、および(\(\ sqrt {3} \)、\(\ sqrt {2} \))for c 。 m を使用しました =1、ω 0 =1、ω =5、γ =0.35、 f d =1、\(\ hbar =1 \)、φ =0、およびγ G (0)=0。フェーズとすべてのパラメーターは便宜上無次元であると見なされ、この規則は後続の図にも適用されます。 A 0 古典的な振幅 X で与えられます c 、0 補完関数の[式を参照してください。 (12)]、振動振幅が大きいと幾何学的位相が大きいことがグラフィックから確認できます。 γの変動もわかります G ( t )μの値が大きくなると大きくなります およびν 式で与えられる条件下で増加します。 (14)
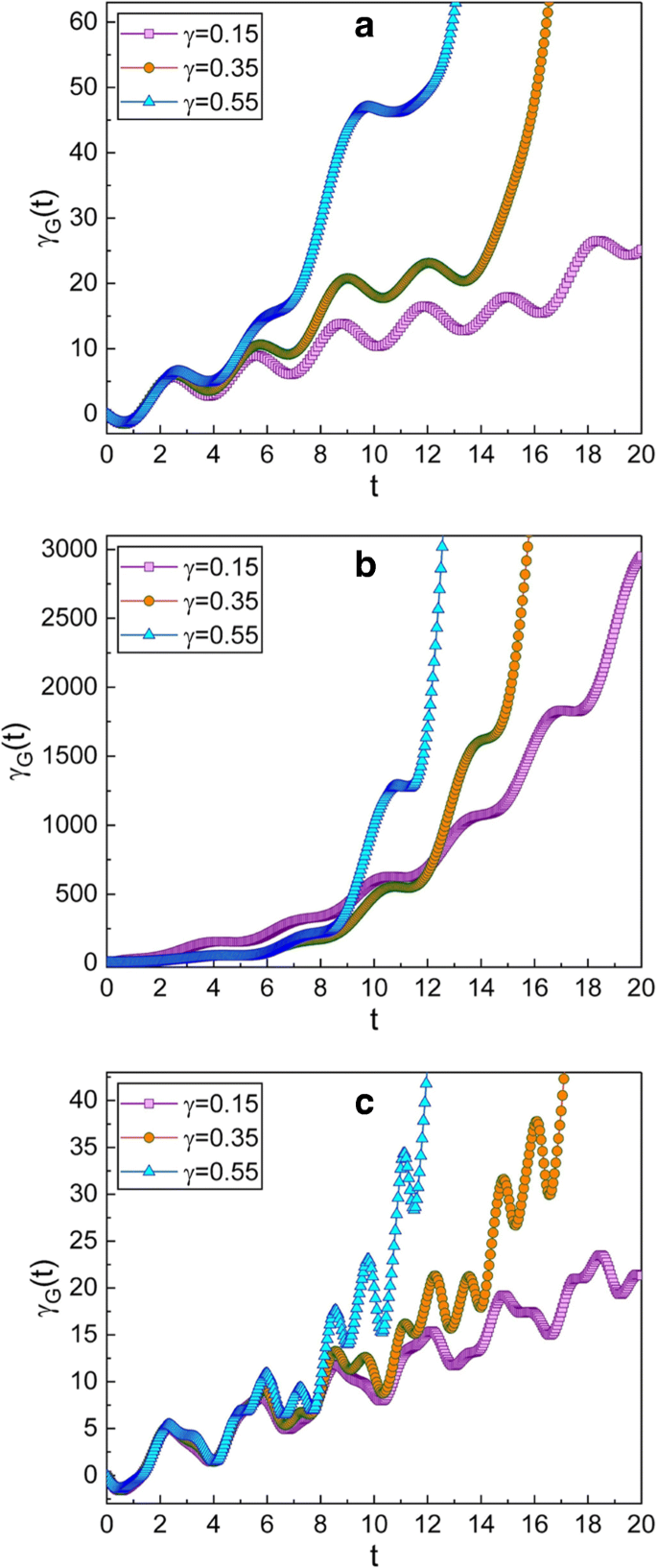
γのいくつかの異なる値に対する幾何学的位相の時間発展 。 ωの値 グラフィックで使用されているのは a の0.3です 、 b の場合は0.99 、および c の場合は5 。ここで選択した絞り込みパラメータは、\(\ mu =\ sqrt {2} \)とνです。 =1;この選択により、 q が得られます -初期時のスクイーズド状態。私たちが使用した他の量は m =1、ω 0 =1、 A 0 =1、 f d =1、\(\ hbar =1 \)、φ =0、およびγ G (0)=0。減衰係数γの場合、幾何学的位相が大きいことを確認します。 ほとんどの場合大きいですが、すべてではありません。ケースの頻度 b は共振周波数に近いのに対し、 a および c 共鳴するものからはほど遠いです。共振の場合の幾何学的位相( b )時間の経過とともに非常に急速に増加します
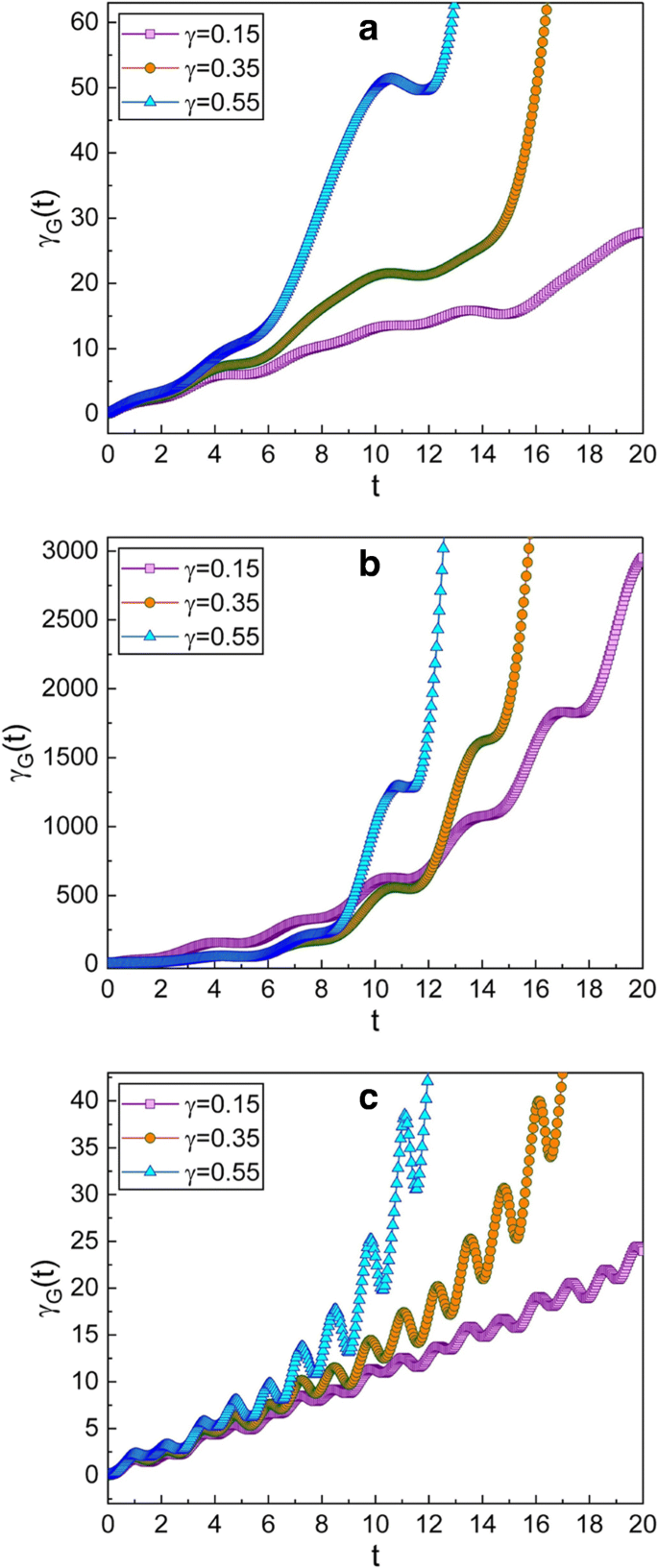
a – c この図は図2と同じですが、選択した絞り込みパラメーターが\(\ mu =\ sqrt {2} \)およびνの場合です。 =-1これは p を与えます -初期時のスクイーズド状態。この場合の全体的なグラフィックは、図2の対応するグラフィックとそれほど変わらないという事実から、γの進化を確認できます。 G ( t )μの絶対値である限り、絞りの種類とはほとんど関係ありません。 およびν 変更しないでください
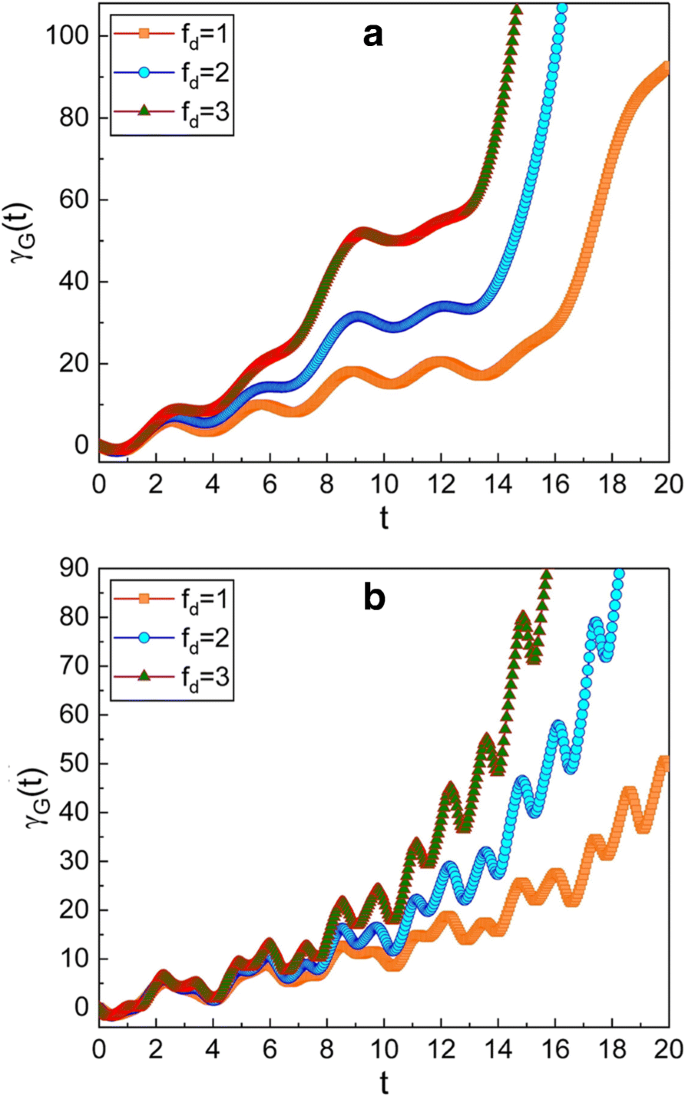
f のいくつかの異なる値に対する幾何学的位相の時間発展 d 。 ωの値 グラフィックで使用されているのは a の0.3です b の場合は5 。 \(\ mu =\ sqrt {2} \)、νを使用しました =1、 m =1、ω 0 =1、γ =0.3、 A 0 =1、\(\ hbar =1 \)、φ =0、およびγ G (0)=0。振幅として( f d )駆動力が大きくなると、幾何学的位相が大きくなります
スクイーズパラメータ c に応じた、スクイーズド状態でのスクイーズ効果 ここで c =μ / ν 参考文献で調査されています。 [39]。参考文献で与えられた分析によると。 [39](参考文献[39]の図1(a)を参照)、\(c =\ sqrt {2} \)に対応する図2に示されているスクイーズド状態は q <です。 / i> -初期のスクイーズド状態ですが、図3の\(c =-\ sqrt {2} \)に対応する状態は、 p です。 -同じ状況でスクイーズド状態。図を比較することによって。 2と3を相互に比較すると、 q の幾何学的位相は次のように結論付けることができます。 -スクイーズド状態は、 p の状態とほぼ同じです。 -スクイーズド状態。
γの効果 幾何学的位相の進化については、図1および2から確認できます。 2および3。γの場合、幾何学的位相はより急速に増加します。 は大きい。図を比較することによって。図2aおよび3aと図2aおよび3a。 2cと3cでは、ωの場合、幾何学的位相がいくらか急速に変化することが確認できます。 共振角周波数よりも大きいです。
システムの共振状態またはその近くでの幾何学的位相の時間的振る舞いは非常に興味深いかもしれません[22、23]。図2bおよび3bは、ωのときに幾何学的位相が非常に急速に増加することを示しています。 共振角周波数に近いです。これは、幾何学的位相の大きさが波動関数の時間変化に関連しているため、この状況での波動関数が時間とともに大幅に変化することを意味します。実際のところ、ワイヤ振動の振幅は、共振状態で著しく増大します。ちなみに、吊り下げられたCNTベースのナノワイヤ共振器の共振角周波数は高いだけでなく、非常に高品質の係数で広く調整可能です[3]。このため、システムの振動モードは、完全に減衰するまで長期間保持されます[11]。
図4は、幾何学的位相が駆動力 f の振幅によっても影響を受けることを示しています。 d 。 f として d 増加すると、時間の幾何学的位相の増分が速くなります。
結論
シュレディンガー方程式を用いた量子力学に基づいて、システムのスクイーズド状態の幾何学的位相を調査しました。システムを記述するハミルトニアンの時間依存性に関して、不変演算子法が導入されました。これは、ハミルトニアンが時間で記述される場合の量子解を導出するための潜在的なツールです。この方法により、CNTベースのナノワイヤ振動の幾何学的位相の解析式が得られました。
機械的振動の理論的理解に必要な位相効果の詳細な分析が実施されました。幾何学的位相の開発は、厳密な数学的評価を備えた完全な量子ベースのものです。幾何学的位相は、機械的パラメータの変化に敏感であり、多くの場合に振動を示します。幾何学的位相の進展に対する圧搾パラメータの影響も分析されています。共振角周波数付近で、時間の経過とともに幾何学的位相蓄積が大幅に増加することを確認しました。
私たちの結果は、CNTベースのナノワイヤの振動に現れる幾何学的位相の時間的挙動を示しています。この研究で与えられた幾何学的位相の分析は、システムのトポロジー的特徴だけでなく、他のナノワイヤーベースの機械的振動子の動的振動も理解するために重要です。特に、共鳴状態の相特性を開発しましたが、量子情報技術やその他の量子ベースの産業でのシステムの応用においては、その解明が必要です[40]。この研究で使用された同様の方法とフレームワークは、超伝導ファブリペロー共振器[41]、ナノカンチレバー[42]、量子ビット-共振器-原子ハイブリッドシステム[43]などの他のナノシステムにも拡張できます。
>略語
- CNT:
-
カーボンナノチューブ
- EMウェーブ:
-
電磁波
- TDHS:
-
時間依存ハミルトン系
ナノマテリアル



