メタ表面/グラフェンハイブリッド構造の表面インピーダンス

はじめに

近年、異常な電磁特性を示す新しい人工インピーダンスメタサーフェスが提案され、以前の文献で調査されました[1,2,3,4,5,6]。一方、ホログラフィー[1]、高解像度イメージング[2]、カーペットマント[3]、吸収体[4、5]など、さまざまな種類のメタサーフェスアプリケーションが導入されています。メタ表面は、薄いテラヘルツおよび光学デバイスを実現する上で重要な役割を果たすことができます。それにもかかわらず、メタサーフェスによる分散応答のため、多くのデバイスは単一の周波数帯域でしか機能できず、狭いスペクトルを調整することはできません。ごく最近、テラヘルツや光周波数などの広範囲の周波数で印加電圧を変化させることにより、導電率を動的に制御できる[7,8,9,10]。そのため、グラフェンはチューニングの最適な候補であることが証明されました。プラズモンおよびメタ表面構造の特性[11]。したがって、メタサーフェスとグラフェンによって設計された多くのデバイスが提案されています[12、13、14]。

その間、メタ表面またはグラフェンシートの等価インピーダンスを計算するためのいくつかの分析モデルが、物理的メカニズムを説明するために採用されてきました[8、15、16、17、18、19、20]。グラフェンまたはメタサーフェスモデルの励起に使用される平面波。分析と計算の2つの異なる方法に分けることができます。計算法はフロケ式の研究です[21、22]。この方法を使用する利点は、構造の形状に制限されないことです。最も重要なメリットの1つは、正確な結果を提供できることです。それにもかかわらず、この方法を使用する商用ソフトウェアは、かなりの時間と計算リソースを消費します。一方、より正確で正確な分析方法が開発されており[23、24、25、26、27]、使いやすく、物理現象のより良い分析を提供します。上記の利点にもかかわらず、特定のメタサーフェスユニットの高精度分析モデルを実現するという課題も顕著です。幸いなことに、等価表面インピーダンスを予測するためにかなりの努力と作業が行われ、多くの優れた結果が得られました[16、28]。ただし、著者の知る限り、このハイブリッドの組み合わせの表面インピーダンスを予測できる分析モデルはまだわかっていません。

この論文では、3D人工吸収体を利用して、メタサーフェスとグラフェンの関係を考慮したメタサーフェス/グラフェンハイブリッド構造のインピーダンスを分析および予測しました。メタサーフェスの表面インピーダンスを高速に計算するために、最初に解析式が開発されました。これらの単純で正確な分析式により、インピーダンス設計に関する完全な解明と基本的な要件が可能になります。次に、グラフェンシートのインピーダンスが計算されます。最後に、メタ表面のサイズと化学ポテンシャルμの関係に焦点を当てます。 _c 、および複合構造のインピーダンス。ここでは、メタサーフェス/書記素ハイブリッド構造の表面インピーダンスについて、その実数成分と虚数成分を計算することによって説明します。私たちの知る限り、このメカニズムを包括的に報告している文献はほとんどありません。

メソッド

正方形パッチとグラフェンシートのインピーダンス

メタ表面グラフェン吸収体の一般的な構造を図1aに示します。この単純な構造の吸収体は、表面マイクロマシニングによって簡単に製造できます。この構成では、薄い導電性メタ表面-グラフェンハイブリッド層と金属グランドプレーンが、スペーサーとしての誘電体基板によって分離されています。地面までの距離は h 。波長（アレイ D の周期）と比較した小さなサイズの正方形パッチの場合 ≪ λ ）とパッチは狭いスロット（スロットの幅 D ）で区切られています − w ≪ D ）、現在のモデルは有効です。伝送線路理論によれば、吸収構造の等価回路モデルを構築することができ（図1bに示す）、これによりメタ表面グラフェンをモデル化することができます。送電線、短絡、およびグリッドインピーダンス Z _mg それぞれ、誘電体基板セクション、グランドプレーン、およびトップパターンハイブリッド層の表面インピーダンスをモデル化します。伝送線路理論によると、入力インピーダンス Z _in この吸収体の量は次のように確立できます：

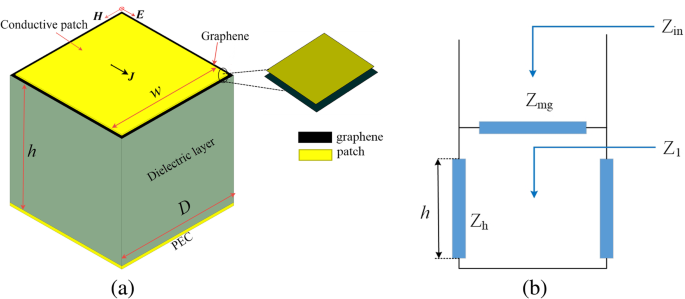
a メタ表面-グラフェン吸収体ユニットセルの概略図。 b ローカル等価回路モデル

ここで Z _h および k _zh は、それぞれこの領域の基板層のインピーダンスと伝搬定数です。次に、垂直入射での吸収率は次のように計算できます

メタ表面グラフェンシートのインピーダンスは、シミュレートされた反射係数から抽出できることは明らかです。導電性パッチのサイズと化学ポテンシャルの関係μ _c 見つけることができます。

正方形パッチのインピーダンス

平面波がメタサーフェスに垂直である場合、平面パッチのアレイは容量性グリッドとして機能します（図1aを参照）。表面インピーダンス Z _m 平均電流強度に関連する正方形パッチの電磁特性として説明できます< J 〉と平均電界強度〈 E 〉パッチ面で：

損失のある純粋な抵抗膜方式のシートインピーダンスの場合 Z _s （im Z _s =0）、法線入射でのパッチの等価インピーダンスは Z で表されます。 _m 、および次のように表すことができます[9、18]：

ここで、\（{\ eta} _ {\ mathrm {eff} =} \ sqrt {\ mu_0 / {\ varepsilon} _0 {\ varepsilon} _ {\ mathrm {eff}}} \）は均一なホストの波動インピーダンスを表します中、および D / w は幾何学的要素です。実効比誘電率は次のように概算できます

さらに、グリッドパラメータα 理想的に導電性のパッチの電気的に密なアレイの場合、次のように書くことができます

\（{k} _ {\ mathrm {eff}} ={k} _0 \ sqrt {\ varepsilon _ {\ mathrm {eff}}} \）は、有効なホスト媒体の波数です。空き領域では、μ ₀ 、ε ₀ 、および k ₀ はそれぞれ透磁率、誘電率、波数です。さらに、関係（4）は、波長λの場合に有効であることを指摘しておく価値があります。 D よりはるかに大きい 。

式（2）によれば、等価インピーダンスは材料シート抵抗だけでなく、アレイ周期 D によっても決定されることがわかります。 幅 w 構造パラメータの。このような分析式の確実性を検証するために、全波シミュレーションによって得られた結果が提示され、分析ソリューションと比較されます。ここで説明するシミュレーションは、市販のソフトウェアAnsoftHFSSを使用して実行されました。メタ表面グラフェン吸収体ユニットセルの反射特性を得るために、周期境界条件とフロケポートを実装しました。シミュレーション中、 Z を使用した純粋な抵抗膜方式のシートインピーダンス _s =35Ω/ sqが厚さ h で基板上に堆積されます =20μm、長さ D =20μm、およびεの比誘電率 _r =3.2（1 − j 0.045）。パッチインピーダンスを抽出するために Z _m 、シミュレートされた入力インピーダンス Z 間の関係による _in 接地された誘電体スラブの表面インピーダンス Z _{g d} 、メタサーフェスパッチのインピーダンスは次のように表すことができます。

ここで Z _gd = jZ _d tan（ k _d h ）、\（{Z} _d =\ sqrt {\ mu_0 / {\ varepsilon} _0 {\ varepsilon} _r} \）は、スラブの特性インピーダンス\（{k} _d =\ omega \ sqrt {\ mu_0 {\ varepsilon} _0 {\ varepsilon} _r} \）は、TEMモードの基板の表面に直交する伝搬定数です。

分析結果は、図2に示すように、抽出された反射係数に基づいてシミュレーション結果と比較することによって検証されます。黒い曲線はシミュレーション結果を示し、赤い曲線は提案された分析式を使用して計算されます。シミュレーション結果と理論的予測の間にはわずかな違いがありますが、これは式（1）によるものです。 （3）は近似式です。全体的な傾向は同じです。したがって、このモデルの分析式の妥当性と正確性を確認します。

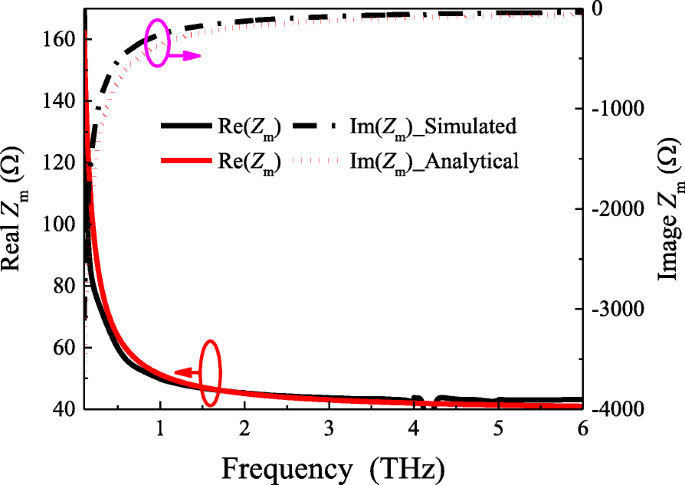
w を使用したパッチアレイのシミュレーションおよび分析グリッドインピーダンス =19μm

パッチサイズがインピーダンス Z に与える影響を調査するため _m 式（2）の有効性を検証し、追加の数値シミュレーションを実行しました。図3は、グリッドインピーダンス Z の実数部と虚数部をプロットしたものです。 _m ユニットセルのさまざまな幾何学的パラメータ。図3aから、インピーダンスの実数部 Z _m パラメータ w として減少します 17から19.5μmに増加します。 Eq.2によると、 Z の実数部が _m パッチの長さに反比例します w 。ただし、虚数部は点線で示されているのとは逆の傾向を示しています（図3bに示されています）。式を考慮に入れる。 （2）と（3）では、虚数部は次のように与えることができます

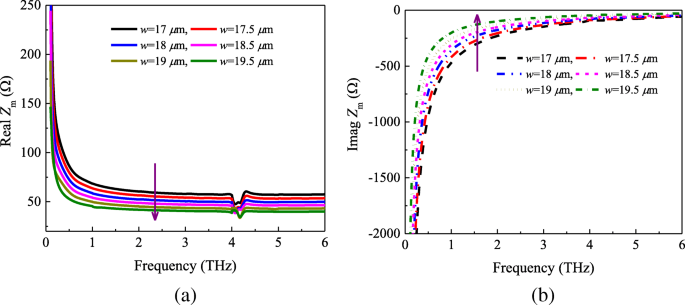
a 本物と b インピーダンスの虚数部 Z _m パッチのサイズが異なる

関係（8）から、 w インピーダンスの虚数部である17から19.5μmに増加します Z _m 増加します。

グラフェンシートのインピーダンス

グラフェンは、非常に薄い表面として見ることができます。外部静磁バイアスと空間分散がない場合、表面伝導率σ _g 、[29]

ここで、ℏは縮小プランク定数、 e 電子の電荷 k _B はボルツマン定数ですが、μ _c 、ω 、τ および T は、それぞれ化学ポテンシャル、角周波数、緩和時間、および温度です。ここでは、 T を想定しています。 =300Kおよびτ =この調査全体で0.1ps。グラフェンのシートインピーダンスは次のように計算できます

ここで R _g および X _g 表面抵抗とリアクタンスです。

グラフェンのシートインピーダンスは、式（1）に従って計算されます。 （9）と（10）。図4は、表面インピーダンスと化学的μの実数成分と虚数成分を示しています。 _c 。 μの増加に伴い、表面抵抗とリアクタンスが連続的に減少することがわかります。 _c 。さらに、化学ポテンシャルが特定の値に固定されている場合、グラフェンシート抵抗の実数部は0.2〜6THzの範囲でほとんど変化しません。

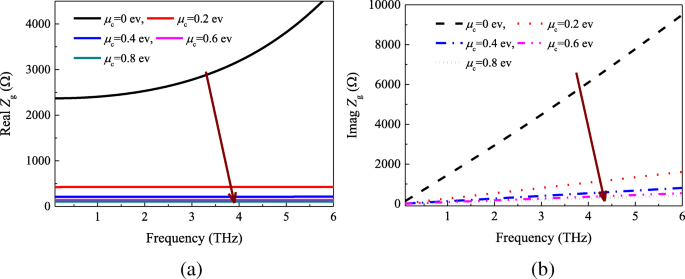
a 本物と b 周波数と化学ポテンシャルの関数としての表面インピーダンスの虚数部

結果と考察

グラフェンシート上の正方形のパッチの場合、このハイブリッド構造の表面インピーダンスを決定する必要があります。以前の文献[8、30、31、32、33、34、35、36、37]では、このハイブリッド構造の表面での総インピーダンス Z _mg 方形パッチインピーダンス Z の並列組み合わせに等しい _m グラフェンシートのインピーダンス Z _g 、つまり Z _mg = Z _m ∥ Z _g 。ただし、シミュレーションと計算により、この関係は無効であることがわかりました。真正性を検証するために、図1aに示すメタ表面グラフェン吸収体ユニットをシミュレートし、式（1）に従ってフィルムの表面インピーダンスを取得しました。図5は、 Z の実数部と虚数部の解析値とシミュレーション値を示しています。 _mg w を使用してさまざまな化学ポテンシャルで =19μm。

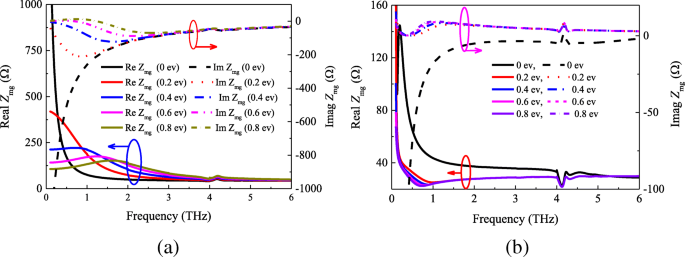
メタ表面-グラフェン膜インピーダンス Z _mg 異なる化学ポテンシャルで。 a 分析および b シミュレーション結果

図5a、bから、分析結果とシミュレーション結果の間に大きな違いがあることがわかります。図5aは、分析結果の実数部が主に40〜500Ωに集中しており、実効インピーダンスの虚数部が− 210〜0Ωの範囲にあることを示しています。それにもかかわらず、図5bによると、インピーダンスの実数部の値は20〜140Ωであり、虚数部の値はμを増やすことで0に近いことがわかります。 _c 0から0.8evまで。ただし、分析結果とシミュレーション結果は、周波数が高くなるとインピーダンスが安定する傾向があるという同じ傾向を示しています。その理由は、周波数が高くなると、グラフェンシートと正方形パッチのインピーダンスが小さくなるためです。 0 evでのメタ表面グラフェン膜のインピーダンスを他の結果と比較すると、インピーダンス Z _mg かなり違います。これは、0 evでのグラフェンシートインピーダンスの値が、より高い化学ポテンシャルとはかなり異なるためです（図4を参照）。

したがって、図5の計算およびシミュレーションされたインピーダンスから、次の結論を導き出すことができます。まず、メタ表面グラフェン膜の表面インピーダンス Z _mg Z の並列の組み合わせと厳密には等しくありません _m および Z _g 。しかし、第二に、それらの間には一定の関係があります。これらの結論を示すために、まず、パッチサイズを変えて図1に示す吸収体の構造をシミュレートします。化学ポテンシャルμのメタ表面グラフェン吸収体の反射係数 _c =0.4 evが図6に表示されています。送電線の理論とモデルによると、インピーダンス Z _mg 取得できる。図7は、取得したインピーダンス Z の実数成分と虚数成分を示しています。 _mg パッチサイズが異なります。図7aによると、パッチの長さが w になると、最初はメタ表面グラフェン膜の実数部が減少することがわかります。 17μmから19.5μmに増加します。ただし、周波数が0.31 THzを超えると、逆の傾向が見られます。一方、図7bは、虚数部の傾向が図7aの前半と同じであることを示しています。さらに、図1と図2を比較します。図4と図5aから、図4と図5aでも同様の状況が見られました。 3と7。それはまた、上記の結論を直接証明します。

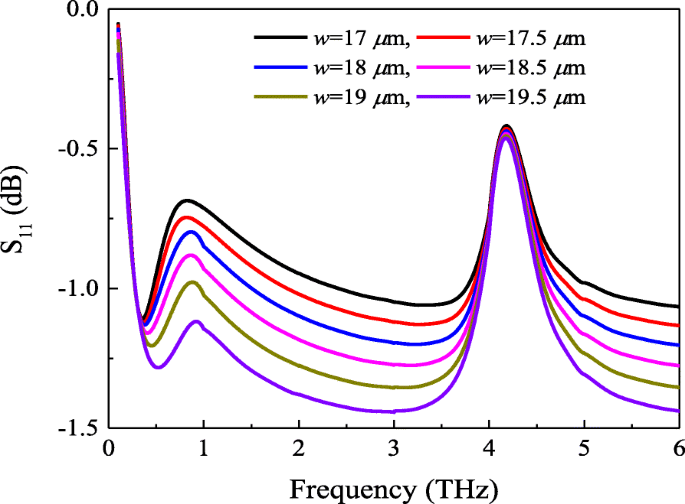
化学ポテンシャルμのメタ表面グラフェン吸収体の反射係数 _c =0.4 ev

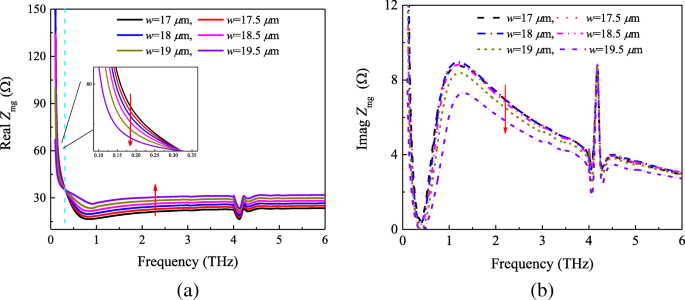
メタ表面-グラフェン膜インピーダンス Z _mg S から取得 -化学ポテンシャルμのパラメータ _c =0.4ev。 a 本物と b 虚数部

パッチサイズの関数としての表面抵抗の物理的起源をさらに調査するために、法線入射でのメタ表面グラフェン膜の表面電流分布を3THzで調査します。図8は、 w の電流強度の変化を示しています。 =17、18、および19μm、化学ポテンシャルμ _c =0.4ev。色はフィールドの強度を表します。明らかに、サイズが大きくなると、表面電流の大きさは減少します。式を考慮に入れる。図3および図7aでは、電界強度が3 THzで固定値の場合、メタ表面グラフェンの膜インピーダンスは次の式で求められます。

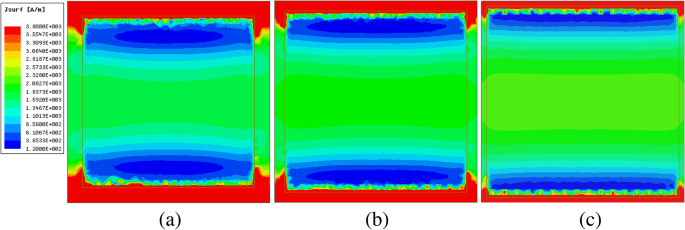
パッチサイズは異なるが同じ周波数の表面電流の大きさ。 a w =17μm、 b w =18μm、および c w =19μm

関係式（11）から、パッチの長さは表面電流の大きさに反比例することがわかります J 。シミュレーション結果と理論結果の間の定性的な一致を明確に観察できます。この物理現象を定量的に分析するために、メタ表面グラフェン膜の表面電流分布の積分値は、HFSSフィールド計算機を使用して計算され、値は1.10e-6、1.07e-6、および1.04e-6Aです。 、 それぞれ。これらの結果は図8と一致しています。

結論

要約すると、THz周波数のメタ表面グラフェン薄膜について、基本的で有効な表面インピーダンスが調査されました。正方形パッチのインピーダンスを計算するための分析式が導き出され、検証されました。メタ表面-グラフェンハイブリッド構造については、抽出された反射係数に基づくシミュレーション結果を、正方形パッチとグラフェンシートインピーダンスの並列組み合わせから得られた分析結果と比較しました。有効インピーダンスに対するパッチサイズの影響を検討するために、追加の分析が実行されました。さらに、パッチサイズとフィルムインピーダンスの関係は、表面電流をプロットして統合することにより、定性的および定量的に説明されました。この分析方法を拡張して、他の2つの異なる導電層のインピーダンス問題を調べることができます。さらに、この作業で行った分析により、アンテナと吸収体に特別に適用するための複合層を分析的に最適化するだけでなく、広範な数値シミュレーションを回避できます。

略語

HFSS：

高周波構造シミュレーション

TEM：

横電磁

THz：

テラヘルツ