短周期CdO / MgO超格子のバンドギャップ研究

はじめに

酸化物や窒化物などの広帯域ギャップ半導体は、現代のオプトエレクトロニクスにとって非常に重要な半導体のファミリーであり、短波長発光ダイオード、レーザーダイオード、光検出器、および高出力、高温、高電界効果トランジスタなどの周波数電子デバイス[1]。エネルギーバンドギャップは、太陽光発電やオプトエレクトロニクスなどの多くの科学分野で重要な要素です。三元合金は、ランダム結晶または準結晶の短周期超格子として得ることができます[2、3、4、5]。ランダム結晶の場合、一部のシステムでは、相と濃度を分離せずに全組成範囲の材料を得ることに重大な問題があります。この種の問題は、ZnMgOおよびZnCdO [6]酸化物系の場合に報告されています。特に、ZnOは通常ウルツ鉱構造で結晶化するのに対し、CdOとMgOは岩塩立方構造で結晶化するためです[7]。したがって、これらの材料の場合、中間組成範囲で結晶相偏析のない均質な合金を得ることが課題であることが証明されています。これは酸化物だけに関係するものではありません。同様の問題も報告されています。たとえば、InGaN [8]の場合です。

岩塩結晶構造を持つCdOは、透明導電性酸化物（TCO）の1つです。 CdOの主な欠点の1つは、固有の直接バンドギャップがわずか2.2eVと比較的小さいことです。伝導帯の自由キャリアによって引き起こされるバースタイン-モス効果は、最も高濃度にドープされたCdOで吸収端を約3 eVにシフトさせる可能性がありますが[9、10]、これは、太陽スペクトル。したがって、CdOのバンドギャップを開くことで、太陽電池技術の見通しが改善されます。ソーラーブラインドUV検出器のカットオフ動作波長は280nmより短くする必要があります。これは、4.5 eVのバンドギャップ値に対応します[11]。これは、たとえば、純粋なCdOとZnOのバンドギャップ（3.37 eV）よりもはるかに大きくなります。 ）。したがって、CdOバンドギャップを開くこともこの分野にとって重要です。

超格子を使用すると、組成をより正確に制御でき、多くの半導体システムで幅広い組成の高品質の三元合金を得ることができます[2、5、12、13]。光電子デバイスの設計に不可欠なバンドギャップエンジニアリングは、層の厚さを変えることによってSLで実現できます[3、14]。 CdOでは2.5eVの直接バンドギャップが報告されていますが、MgOの場合、岩塩構造では7.8eVのエネルギーギャップが観察されました[15]。理論的には、岩塩の立方構造は、二元酸化物の好みから予想されるように、すべての（Mg、Cd）O組成にわたって安定しています[16]。ただし、通常、CdO層はMgOよりもはるかに低い温度で成長します。したがって、全組成範囲にわたって均質な混合結晶を得ることが問題である。このため、CdMgO合金に関する報告の数は非常に限られており、有機金属化学蒸着（MOCVD）によって成長したCdMgOの場合に説明されているように、Cdの量を増やすと2つの組成が存在する可能性があります[17 ]。マグネトロンスパッタリングにより、総Mg濃度が44％ものCdMgO合金薄膜が得られました[18]。パルスレーザー堆積技術によって得られた層の場合、CdMgOのエネルギーバンドギャップは3.4 eVにシフトしました[19]が、多結晶InドープCdMgO膜では、エネルギーギャップの最大値は約5eVであると報告されています[19]。 20]。組成範囲の反対側では、ドープされていない、1％、2％、および3％のCdドープMgOナノ構造が、連続イオン層吸着および反応（SILAR）法によって成長しました[21]。全組成範囲でナノ粒子のみが得られましたが、それでも0.34≤ x のMg含有量の範囲にあります ≤0.84Cdに富むCdとMgに富むCdの2つの相の共存 _{1- x} Mg _x Oが報告されています[22]。

最近の理論的研究は密度汎関数理論計算に基づいており、構造[23,24,25]、電子[26]、分光法[27]、光学[27]の調査を含む、主にCdOとMgOの二元化合物の特性に専念しています。 28,29,30]、磁気[31,32,33,34,35]またはドープされた化合物の他の特性[36,37,38]、Gorczyca etal。 [13、14]は、ZnO / MgOSLのバンドギャップ工学調査を実施しました。 CdO / MgO超格子の理論的調査は文献で報告されておらず、この事実が私たちにそれらを研究する動機を与えました。

以前の研究では、分子線エピタキシー（MBE）によって{CdO / MgO} SLを取得する可能性を示しました[39]。この研究では、CdOベースのTCOの透明度を、同じ（岩塩）結晶構造を持つより大きなバンドギャップの金属酸化物であるMgOと合金化することにより、実験的および理論的に調整する方法を検討します。組成範囲全体でMBEによって{CdO / MgO}超格子（SL）準合金を成長させ、これらの超格子のCdO超格子の厚さを変更することで、エネルギーギャップを2.2から6eVに増やすことができることを示しました。

メソッド

短周期{CdO / MgO} SLは、プラズマ支援MBE（Compact 21 Riber）によって、異なる配向のサファイア基板上で成長しました： c -および r -Al ₂ O ₃ 。成長する前に、Al ₂ O ₃ 基板は、700°Cのバッファーチャンバーで化学的に洗浄および脱気されました。次に、基板を成長チャンバーに移し、酸素中、700°Cでアニーリングしました（流速3 ml / min）。すべての多層構造は360°Cで成長しました。 CdOとMgOの薄層を順次堆積し、成長条件に基づいてそれらの厚さを推定しました（サンプルの同じ最終厚さを得るために、個々のサンプルの期間数を計算しました）。提示された一連のサンプルでは、​​MgOサブレイヤーの厚さは固定されており、CdOレイヤーの厚さは〜1から〜12モノレイヤー（ML）まで変化します。

Panalytical X’Pert Pro MRD回折計を使用して、サンプルのX線回折（XRD）分析を実行しました。この装置には、ハイブリッド2バウンスGe（220）モノクロメーター、トリプルバウンスGe（220）アナライザー、および2つの検出器（比例およびピクセル）が装備されています。 2種類の測定が実行されました：θ / 2 θ 広角範囲の低解像度設定でスキャンし、ロッキングカーブ、2 / ω 高解像度設定でのスキャンとXRD逆格子空間マップ。

Varian Cary 5000分光光度計を使用して、室温で200〜700nmの範囲の光透過率スペクトルを取得しました。研究対象のフィルムの透過率測定には、2チャンネル測定技術を使用しました。 SLサンプルは、分光光度計の測定チャネルと基板（ r -または c 指向性サファイア）が比較チャネルに配置されました。

結果と考察

実験的研究

4 MLのMgOと1〜12MLの範囲のCdO副格子の厚さを持つ超格子構造を分析しました。図1a、bは、選択した{CdO / MgO} SLのフルレンジXRDスキャンを示しています。 θ / 2 θ パターンは、基板の2つの結晶学的配向を示しました：[01-12]と[0001]（ r -オリエンテーションと c -オリエンテーション）。また、{CdO / MgO}超格子SLの立方晶相を記録しました。 r で成長したサンプルの場合 -[100] {CdO / MgO} SL配向、および c で成長した構造に対して取得した平面サファイア基板 -[111] {CdO / MgO} SL配向を受け取った平面サファイア基板。 {CdO / MgO}材料の他の結晶学的相は観察されません。

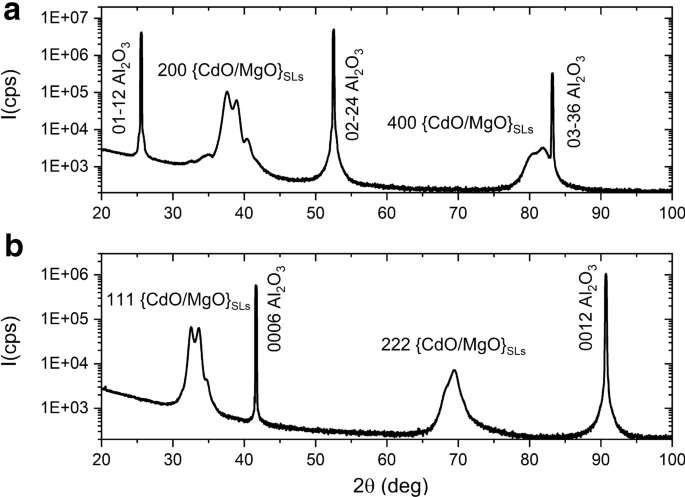
a 上の{CdO（12.5 ML）/ MgO（4 ML）}超格子のTheta–2ThetaXRDスキャン r -Al ₂ O ₃ および b c -Al ₂ O ₃

{CdO / MgO} SLの徹底的な分析のために、2シータ-オメガ（2 θ / ω ）高解像度モードでのスキャンが測定されました。 r で成長したSL構造の場合 -サファイア200 {CdO / MgO} X線回折反射（図2a）と、 c で成長したSL構造について調査しました。 -サファイア111 {CdO / MgO} X線回折反射を調査しました（図2b）。図2の実線は測定結果を示しています。超格子に関連する衛星のピークが両方の方向ではっきりと観察され、界面の良好な周期性と滑らかさが確認されています。 SLの平均パラメータを表すゼロ次ピークは S としてマークされます ₀ 。 S の位置 ₀ ピークはCdOサブレイヤーの厚さに依存します。衛星のピーク（ S ₁ 、 S ₂ ）は両方のサンプルで明確に定義されています。 2 θ / ω XRDスキャンは、SL（ S ₀ 次数ピーク）は、Cd濃度の増加に伴い、より小さな角度にシフトします。これは、Cd含有量が高くなるにつれて格子定数が増加していることを示しています。

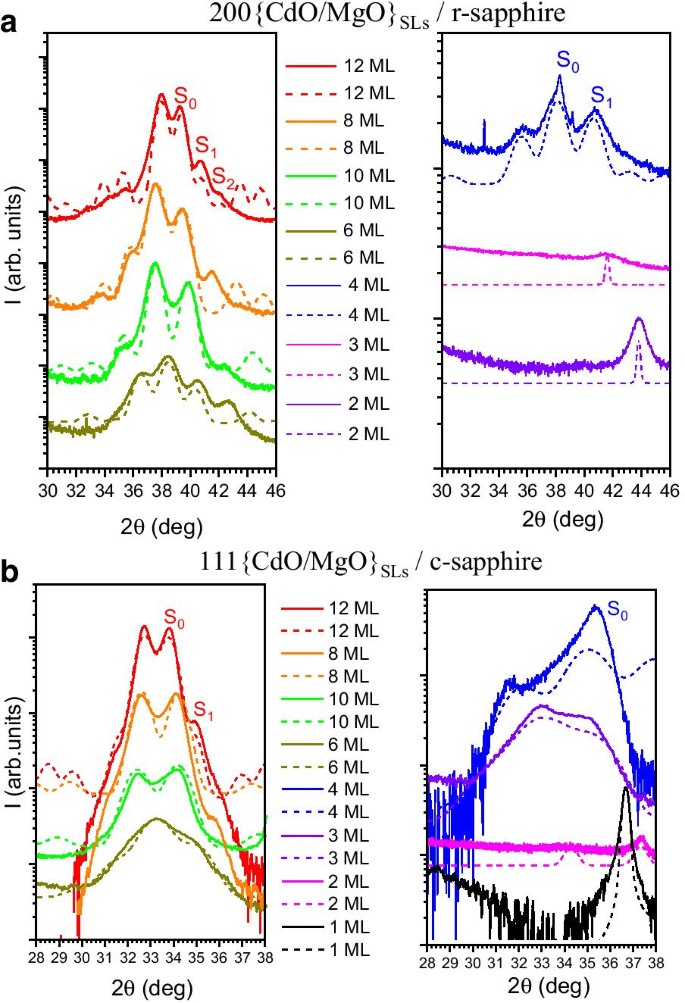
2シータ-r-Al ₂ 上の200 {CdO / MgO}のオメガ O ₃ （ a ）および111 {CdO / MgO} on c-Al ₂ O ₃ （ b ）CdO層の厚さが異なる一連のSLのXRDピーク。実線は2 θです / ω XRDスキャンの測定結果と破線は2 θです。 / ω XRDスキャンシミュレーション。凡例では、CdO単分子層（ML）の量を示しています

測定された2 θごとに / ω スキャンして2 θを計算します / ω [40]で説明されているフィッティング手順を使用したプロファイル。図2に、2 θを示します。 / ω 破線によるXRDスキャンシミュレーション。シミュレーション手順は、Takagi and Taupin [41,42,43]によって記述されたX線回折の動的理論に基づいています。 Malvern Panalytical社が提供するX’Pert Epitaxyソフトウェアを使用して、2 θをシミュレートします。 / ω 曲線。表1で収集したシミュレーションデータから得られた結果。

XRDシミュレーションから受け取った最も重要なパラメーターは、SL構造の個々のMgOおよびCdO層の厚さです（表1）。 MBE成長プロセス中に想定されたように、MgO層の厚さが各サンプルで2nmに等しいことがはっきりとわかります。 CdO層の厚さについては、想定されるパラメーターとの違いがいくつか見られます。表1に示されているデータは、MLの量で表されたSL内の個々のCdOおよびMgO層の再計算された厚さ（XRDシミュレーションから）を示しています。

{CdO / MgO}準合金フィルムは、UV-可視-赤外分光計で分析され、エネルギーバンドギャップが研究されました。図3は、室温で測定された透過率スペクトルを示しています。 CdO副層の厚さが減少するにつれて、透過のカットオフはより短い波長に連続的にシフトします。 NIR領域での透過率の低下は、自由キャリア吸収とプラズマ反射に関連している可能性があります[44]。ご存知のように、CdOはMgOとは対照的に導電性が高いです。 MgOに対するCdOの相対的な厚さが増加すると、おそらくCdO副層の厚さが増すため、サンプルの抵抗率が増加します。興味深いことに、透過率の低下はSLの向きに依存するため、さらに調査が必要です。エネルギーバンドギャップ値（ E _g ）のSLは、αのグラフを外挿することによって導出されます。 ² 対hν 直接遷移の場合（図4a、b）およびαの場合 ^1/2 対hν 間接遷移の場合、α は吸収係数であり、ν Taucの研究[45]によると、は光子周波数です。 CdOの厚さが厚く、CdMgO合金のCd濃度が比較的高いサンプルでは、​​図4c、dに示すように、2つの線形領域を持つ2つの間接バンドギャップを抽出できます。図4は、CdMgOのバンドギャップがCdOの厚さとともに減少することを示しています。光透過率の測定は、{CdO / MgO}準合金の直接エネルギーバンドギャップが2.6〜6eVの範囲で変化する可能性があることを示しています。

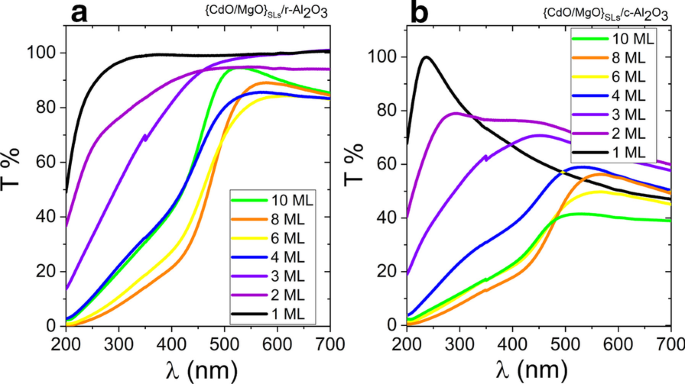
（ a 上の{CdO / MgO} SLフィルムの透過率 ） r -サファイアと（ b ） c -サファイア

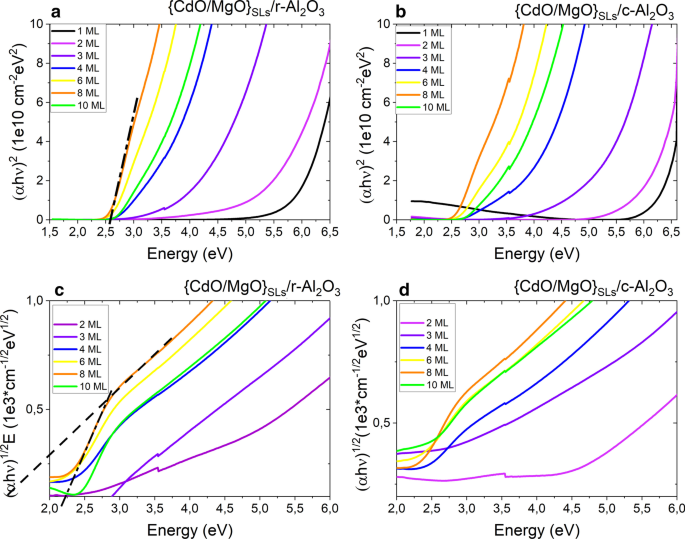
（α hν ） ² および（αhν ） ^1/2 光子エネルギー（hν）の関数としてプロット ） c の{CdO / MgO} SLフィルムの場合 -または r -サファイア

計算方法

ここで報告されているすべての計算では、以前の調査に続いて、量子密度汎関数形式に基づくウィーンab Initioシミュレーションパッケージ（VASP）が使用されました[46、47、48]。イオン位置の最適化は、交換相関エネルギーに異なる一般化勾配近似（GGA）汎関数を使用して、2段階で実行されました。エネルギーカットオフが605eVの標準平面波関数基底関数系が使用されました。 Monkhorst–Packグリッド（5×5×5）は、k空間での効率的な統合に使用されました[49]。 Cd、Mg、およびO原子の処理には、Perdew、Burke、およびErnzerhof（PBE）交換相関汎関数を使用したProjector-Augmented Wave（PAW）擬ポテンシャルが使用されました[50、51、52]。電子自己無撞着（SCF）ループは、10 ^–7 未満の相対的なエネルギー変化で終了しました。 。バルク酸化物のabinitio格子定数は次のとおりです。 a _CdO =4.783Å、 a _MgO =4.236Å。これらの格子定数は、X線測定によって決定された値とよく一致しています： a _CdO =4.695Å、 a _MgO =4.21Å[15、53]。単一の原子に作用する力の大きさが0.005eV /Å未満になるまで、原子の位置を緩和しました。

PBE密度汎関数は、半導体のバンドギャップに誤った値を提供します。この欠陥を取り除くために、（GW）近似[54]、Hartree-Fock補正を使用した混成汎関数[55]、または半占有一般化勾配近似（GGA-1 / 2）[56]などのいくつかの方法が使用されています。 。報告された計算では、Ferreira etalによって提案された最も効率的な後者のスキームを使用しました。 [56]。これらの計算では、スピン軌道相互作用は無視されました。これは、高位の原子価状態と低位の伝導状態により、小さな分裂（10 meVのオーダー）が発生するためです。バルクMgOとCdOの計算されたバンドギャップは E でした _Γ （MgO）=7.1eVおよび E _Γ、L （CdO）=2.55、1.23 eV、それぞれ。したがって、低温実験バンドギャップとの十分な一致が得られました： E _g （MgO）=7.83 eV [15]および E _Γ、L （CdO）=〜2.5、0.8–1.12 eV [57、58]。これで、前述の第2段階が完了し、PBE近似を使用して第1段階で原子の位置と周期的なセルサイズが決定された構造に、修正されたGGA-1 / 2補正方法を適用して最終結果が得られます。 。 PBEおよびGGA-1 / 2近似のバルクMgOおよびCdOのバンド構造を図5に示します。PBEはエネルギーギャップの値を過小評価しているのに対し、GGA-1 / 2では正しく計算されていることがわかります。補正後、フェルミエネルギーは価電子帯の最大値（VBM）と伝導帯の最小値（CBM）の間にあります。 CdOのバンドギャップは、Refsの実験測定と一致しています。 [58]と[57]、MgOのエネルギーギャップは参考文献と一致しています。 [15]。 CdOのフェルミ準位の位置は、GWアプローチに基づく理論モデルと同じです[59]。

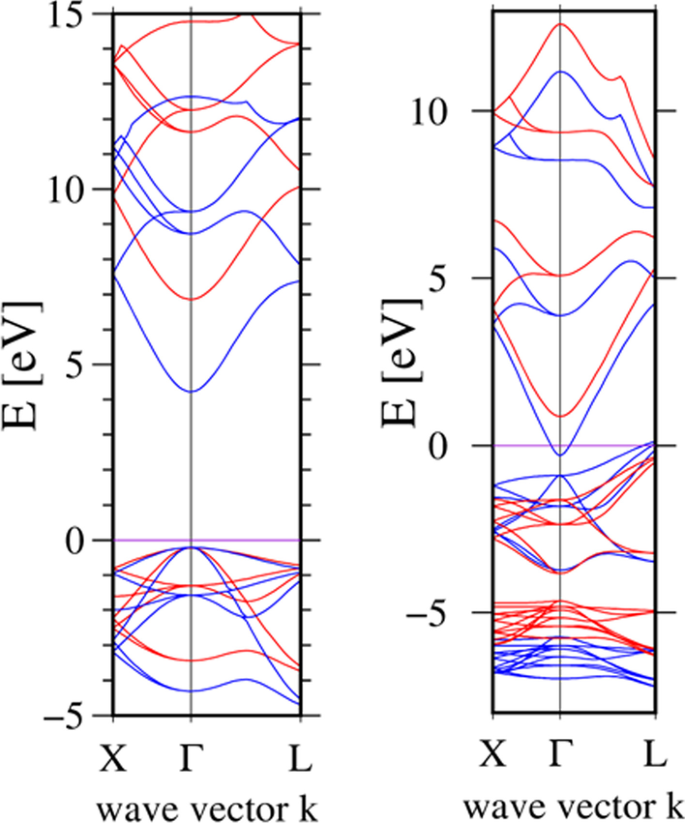
（オンラインカラー）VAPSから得られたPBE（青）交換相関汎関数およびMgO（左）とCdO（右）のGGA-1 / 2（赤）補正のバンド構造

コヒーレントCdO / MgOマルチ量子ウェルの理論的分析では、[001]方向に成長した構造を使用しました。 CdOとMgOの層は完全に歪んでいます。つまり、構造全体に単一の共通の格子定数があり、2つの材料間の界面に転位や欠陥はないと仮定しました。構造は、力を最小化するための共役勾配（CG）アルゴリズムを使用して緩和されました。フェルミエネルギーは構造全体で共通であり、CBMに近いため、キャリア濃度は10 ²⁰ に設定されました。 cm ³ 。 2〜12MLの範囲の4MLのMgOおよびCdO層で構成される構造の一般的な格子定数を計算しました。これらの構造について、GGA-1 / 2補正法を使用して、ブリルアンゾーンの異なるポイント間のエネルギーギャップを計算しました。図6は、 X での伝導帯の最小値と価電子帯の最大値の違いを示しています。 、 L ポイント、および X の近くにある最大値1つ ポイントですが、 X に向かってわずかにシフトしています マークしたポイント〜 X 。

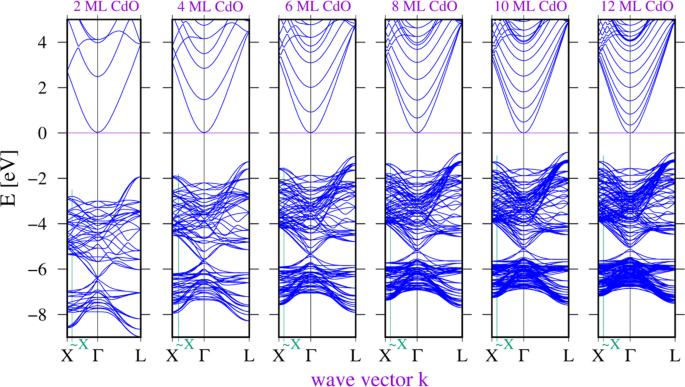
GGA-1 / 2法を使用して、さまざまな数のCdO単分子層および4つのMgO単分子層の立方晶{CdO / MgO} SLのバンド構造を計算しました

ひずみが計算されたバンド構造に影響を与えることは明らかです。図7に、構造で実現されたひずみ条件をプロットします。プロットから、CdO層はMgO層によって成長面で圧縮され、これにより材料が成長方向に伸びます（図7a）。一方、MgO層の面内引張ひずみと面外圧縮ひずみが予想されます（図7b）。

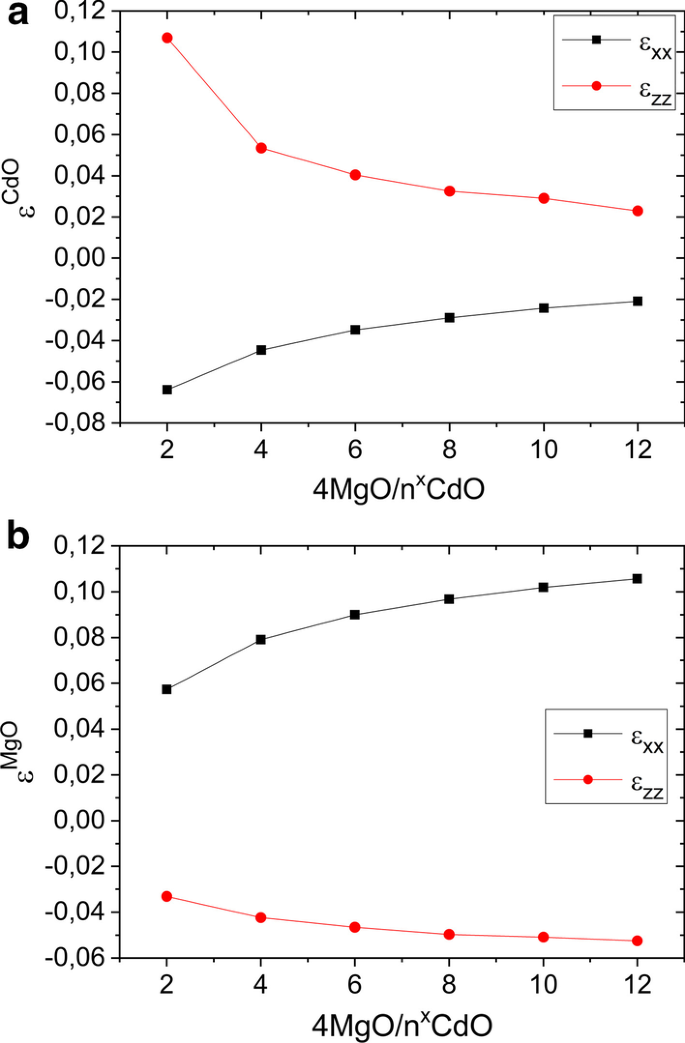
4MLのMgOおよびさまざまな数のCdO単分子層構造の計算されたひずみ条件：（ a ）CdOの面内（イプシロンxx）および面外（イプシロンzz）株。 （ b ）MgOの面内および面外ひずみ

実験と理論の比較

図8では、CdO層の厚さの関数として得られたバンドギャップエネルギーが、計算結果と比較されています。私たちの実験ポイントは、100の場合は満杯、111の方向の場合は開いているとマークされています。黒、赤、青の実線は、理論的に得られたΓ、 X の直接および間接バンドギャップの値を表しています。 および〜 M ポイント。実験データはやや散在していますが、理論的な傾向を反映しています。エネルギーギャップの実験値は、理論的に予測された値よりも高くなっています。 Cdに富む領域を持つCdOベースの層の場合、電子濃度は通常高いことに注意する必要があります[57、60]。キャリア密度の増加がバンド内の状態の充満につながり、したがって吸収開始がより高いエネルギーにシフトすることはよく知られています。この効果は、1954年にモス[61]とバースタイン[62]によって独自に発見され、バースタイン-モスシフト（BMS）と呼ばれています。したがって、CdOベースの材料では、バンドギャップの繰り込みは約9×10 ¹⁸ の電子密度まで考慮する必要があります。 cm ^-3 。 CdO層の厚さが厚いSL構造では、BMSが高くなると予想されます。同様に、SL層の応力は、測定されたバンドギャップエネルギーに影響を与える可能性があります。ご存知のように、MgOとCdOのサブレイヤーが厚い場合、構造は部分的に緩和される可能性がありますが、計算は完全に歪んだSLに対して行われたため、構造全体に単一の格子定数が使用され、転位や2つの副格子材料間の界面の欠陥。フェルミエネルギーは構造全体に共通であり、エネルギーギャップの真ん中にあったため、自由キャリア濃度はゼロに設定されました。 B の計算値 - M 2×10 ²⁰ の電子濃度レベルでの純粋なCdOのシフト cm ^-3 は約300meVであるため、Cdが豊富な構造の場合、測定されたエネルギーバンドギャップから特定の値（<300 meV）を差し引く必要があります。

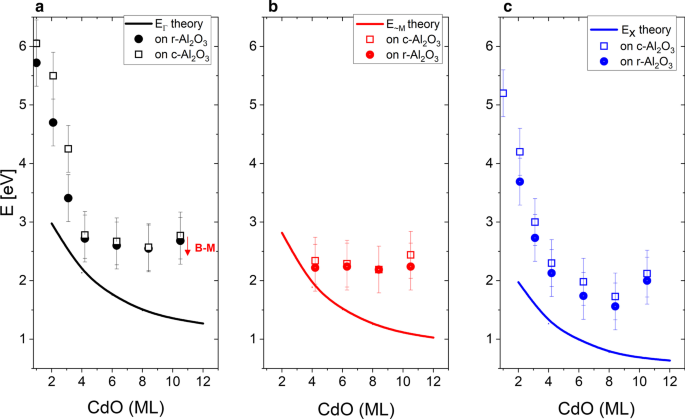
Γ、 X の理論バンドギャップ（実線）の比較 M の近くにあるポイントと最大値 透過率データから得られた点と実験データ（記号）

X線回折の場合、測定されたSLの平均格子定数も差し引きました。測定された格子定数は、CdOサブレイヤーの厚さとともに増加します。得られたデータを図9の理論計算と比較します。実験値は計算値よりも小さいように見えますが、実験データは理論的な傾向を再現しています。

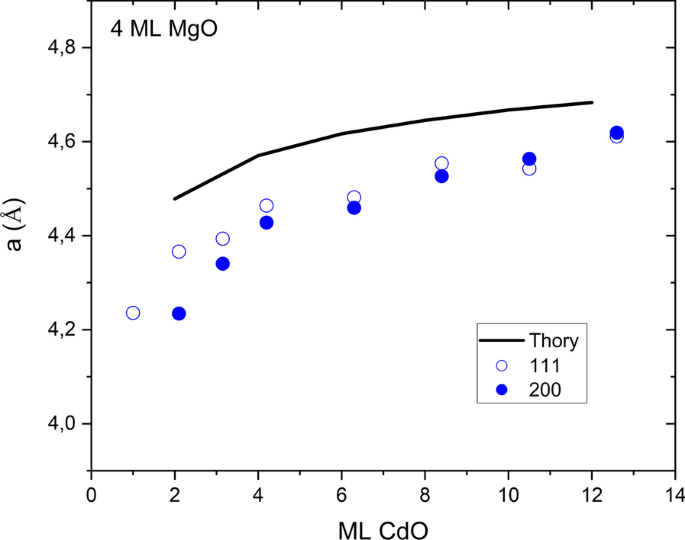
CdOサブレイヤーの厚さが異なる一連のSLの理論格子定数（実線）と実験データ（記号：111方向に成長したサンプルの場合は開いており、001方向に成長したサンプルの場合は完全）の比較

結論

結論として、{CdO / MgO}準合金は、MBE法によって2つの結晶学的配向で合成されました。それらのエネルギーバンドギャップと格子定数特性は実験的に研究され、理論的に計算されました。 {CdO / MgO}準合金のエネルギーバンドギャップは、CdO副格子の厚さを変更することにより、2.6〜6eVの広い範囲で連続的に変調できます。これに対応して、{CdO / MgO}の測定された平均格子定数は、MgOの厚さが一定に保たれ、CdOの厚さが1から12 MLに増加したため、4.23から4.61Åまで変化しました。得られた格子定数の値は理論計算とよく一致していますが、計算値よりもいくらか小さくなっていますが、測定されたエネルギーギャップは完全に歪んだ構造のabinitioで計算された値よりも高くなっています。結果は、{CdO / MgO}準合金を使用することで、CdOのエネルギーバンドギャップをより高い値に調整でき、広い範囲でエネルギーギャップを設計できることを示しています。この研究は、{CdO / MgO}ヘテロ構造が、可視、UV A、UV B、UVC領域の検出器などの新しいオプトエレクトロニクスデバイスの開発に役立つ可能性があることを示しています。

データと資料の可用性

該当なし。