ブール代数単位

数学では、アイデンティティ 1つまたは複数の変数のすべての可能な値に当てはまるステートメントです。

x + 0 =xの代数的単位元は、何でも （x）ゼロに追加 「何でも」の値に関係なく、元の「何でも」に等しい 」（x）は可能性があります。

通常の代数と同様に、ブール代数には、ブール変数の2価の状態に基づいた独自のIDがあります。

加法単位元

ゼロの追加

最初のブールIDは、すべての合計です。 およびゼロ 元の「何でも」と同じです 。」

このアイデンティティは、実数の代数に相当するものと同じです：

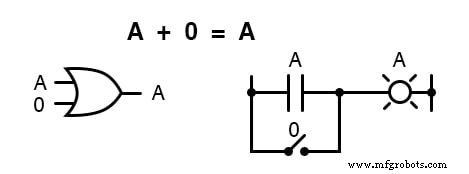
A の値に関係なく 、出力は常に同じになります： A =1 の場合 、出力も 1 になります; A =0 の場合 、出力も 0 になります 。

1つ追加

次のアイデンティティは、通常の代数で見られるものとは間違いなく異なります。

ここで、「何か」の合計がわかります。 」と 1つ 1つです ：

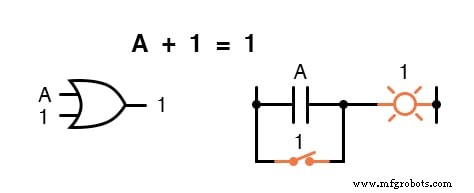
Aの値に関係なく、Aと1の合計は常に1になります。

ある意味で、「1」信号はオーバーライド 論理回路に対するAの影響、出力は論理レベル1に固定されたままになります。

それ自体に数量を追加する

次に、 A を追加した場合の効果を調べます。 および A これは、 ORゲートの両方の入力を接続するのと同じです。 お互いにそして同じ信号でそれらを活性化する：

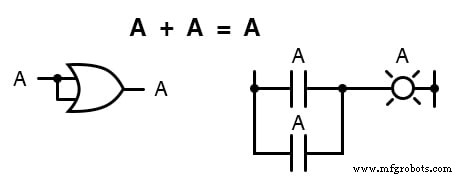
実数代数では、2つの同一の変数の合計は、元の変数の値の2倍になります（x + x =2 x）ただし、ブール数学の世界には「2」の概念はなく、1と0しかないため、 A + A =2A とは言えません。 。

したがって、ブール量をそれ自体に追加すると、合計は元の量に等しくなります： 0 + 0 =0 、および 1 + 1 =1 。

補集合に数量を追加する

加法単位元に補完の一意のブール概念を導入すると、興味深い効果が見つかります。

「 1 」が1つ必要なので 任意の変数とその補数の間の値。ブール値と1の合計は1であるため、変数とその補数の合計は1でなければなりません。

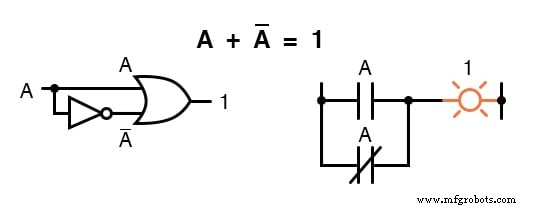
乗法恒等式

4つのブール加法単位元（ A + 0、A + 1、A + A、およびA + A ’）があるのと同じように ）、したがって、4つの乗法恒等式もあります： Ax0、Ax1、AxA、およびAxA ’ 。これらのうち、最初の2つは、通常の代数での同等の式と同じです。

0または1を掛ける

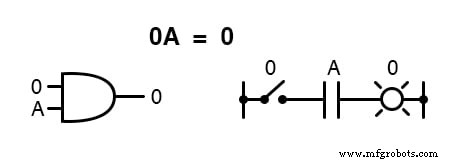
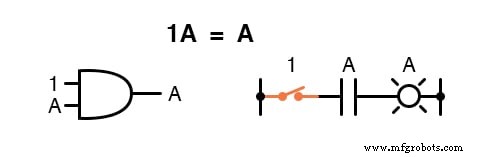
数量をそれ自体で乗算する

3番目の乗法IDは、ブール量にそれ自体を掛けた結果を表します。

通常の代数では、変数とそれ自体の積は二乗 その変数の（3 x 3 =3 ² =9）。

ただし、正方形の概念 は2の量を意味しますが、これはブール代数では意味がないため、 A x A =A ² とは言えません。 。

代わりに、 0 x 0 =0 であるため、ブール量とそれ自体の積が元の量であることがわかります。 および 1 x 1 =1 ：

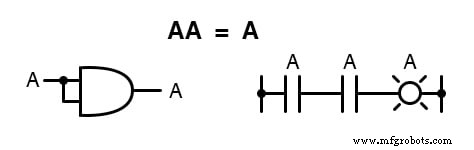
数量にその補数を掛ける

4番目の乗法IDは、ブール数学に固有の概念である変数の補集合を使用するため、通常の代数には同等のものがありません。

「 0 」が1つ必要なので 任意の変数とその補集合の間の値、および任意のブール量と 0 の積以降 0 です 、変数とその補集合の積は 0 でなければなりません ：

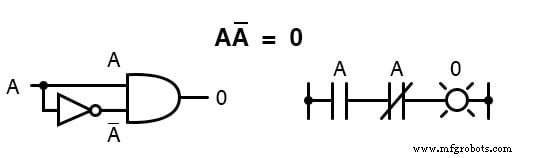
要約すると、加算用に4つの基本的なブールIDがあり、乗算用に4つの基本的なブールIDがあります。

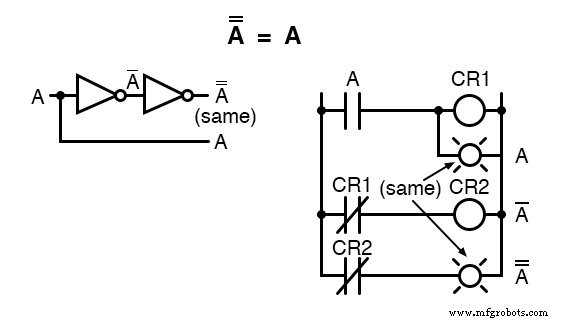
二重補集合

補完に関係するもう1つのアイデンティティは、二重補完のアイデンティティです。 ：変数が2回反転しました。

変数を2回（または任意の回数）補完すると、元のブール値になります。

これは、実数代数の否定（-1を掛ける）に似ています。偶数の否定はキャンセルされ、元の値が残ります：

関連するワークシート：

• ブール代数ワークシート