カルノー図、真理値表、ブール式
カルノー図を作成したのは誰ですか?
電気通信エンジニアのモーリス・カルノーは、1953年にベル研究所でデジタルロジックベースの電話交換回路を設計しながらカルノー図を作成しました。
カルノー図の使用
ベン図を使用してカルノー図を作成したので、それを使用してみましょう。カルノー図削減 論理関数は、ブール代数と比較してより迅速かつ簡単に機能します。削減とは、単純化することを意味し、ゲートと入力の数を削減します。
ロジックを最低のコストに簡素化するのが好きです。 コンポーネントを排除することでコストを節約するためのフォーム。最小コストは、ゲートあたりの入力数が最も少ないゲート数が最も少ないと定義しています。
選択肢があれば、ほとんどの学生は、このツールを学習すると、ブール代数ではなくカルノー図を使用して論理を単純化します。
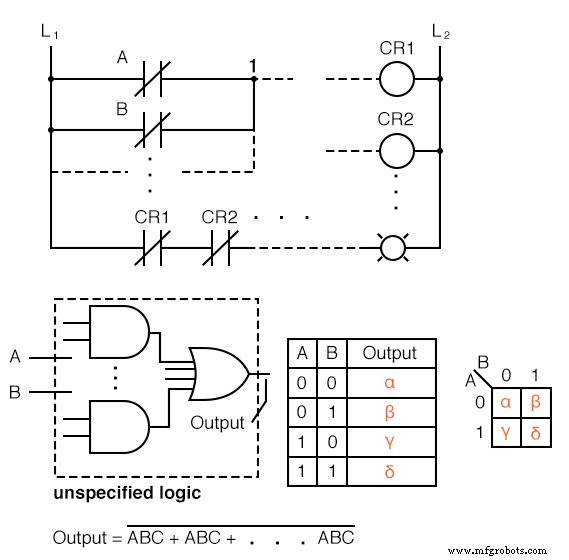
上記の5つの個別の項目を示します。これらは、同じものを表すための異なる方法です。任意の2入力デジタル論理関数です。最初はリレーラダーロジック、次に論理ゲート、真理値表、カルノー図、ブール方程式です。
重要なのは、これらのいずれも同等であるということです。 2つの入力 A および B 0 のいずれかの値を取ることができます または 1 、高または低、オープンまたはクローズ、場合によってはTrueまたはFalse。 2 2 があります =出力を生成する入力の4つの組み合わせ。これは、5つの例すべてに当てはまります。
これらの4つの出力は、リレーラダーロジックのランプ、ゲートダイアグラムのロジックプローブで確認できます。これらの出力は、真理値表またはカルノー図に記録される場合があります。カルノー図を再配置された真理値表として見てください。
ブール方程式の出力は、ブール代数の法則によって計算され、真理値表またはカルノー図に転送されます。
5つの同等の論理記述のうちどれを使用する必要がありますか?タスクを実行するのに最も役立つもの。
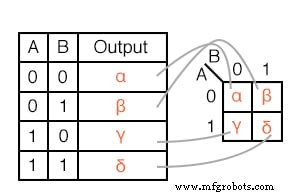
真理値表の出力は、1対1でカルノー図のエントリに対応します。真理値表の先頭から始めて、A =0、B =0の入力は出力αを生成します。
これと同じ出力αが、A =0、B =0セルアドレス、A =0行とB =0列が交差するKマップの左上隅のカルノー図にあることに注意してください。他の真理値表は、入力AB =01、10、11からβ、χ、δを出力し、対応するKマップの場所にあります。
以下に、ブール領域のような以前の長方形のベン図を使用して、2変数Kマップ内の隣接する2セル領域を示します。
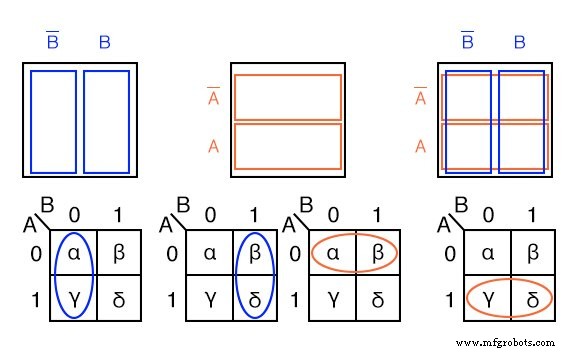
セルαとχは、下の左端のKマップの楕円としてKマップで隣接しています。前の真理値表を参照すると、そうではありません。それらの間に別の真理値表エントリ(β)があります。これにより、Kマップを正方形の配列に編成するという全体的なポイントに到達します。共通のブール変数を持つセルは、私たちに飛び出すパターンを提示するために、互いに近接している必要があります。
セルαとχの場合、ブール変数 B ’があります。 共通して。 B =0 であるため、これを知っています。 ( B ’と同じ )セルαおよびχの上の列の場合。これをKマップの上の正方形のベン図と比較してください。
同様の推論は、βとδがブール値の B を持っていることを示しています (B =1)共通。次に、αとβはブール値の A ’を持ちます (A =0)共通。最後に、χとδはブール値の A (A =1)共通。最後の2つのマップを中央の正方形のベン図と比較します。
要約すると、セル間のブール変数の共通性を探しています。カルノー図は、その共通性がわかるように構成されています。いくつかの例を試してみましょう。
例
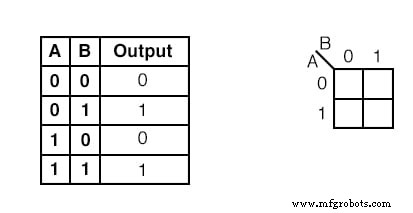
例:
真理値表の内容を上のカルノー図に転送します。
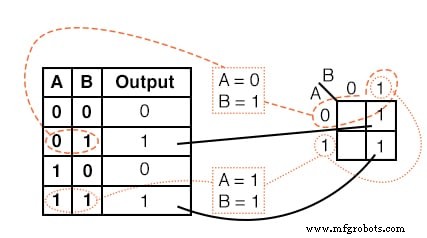
解決策:
真理値表には2つの 1 が含まれています s。 K-マップには両方が必要です。最初の 1 を見つけます 上記の真理値表の2行目にあります。
- 真理値表のABアドレスに注意してください
- 同じアドレスを持つKマップでセルを見つけます
- 1 を配置します そのセルで
1 に対してこのプロセスを繰り返します 真理値表の最後の行にあります。
例:
上記の問題のカルノー図については、ブール式を記述します。解決策は以下のとおりです。
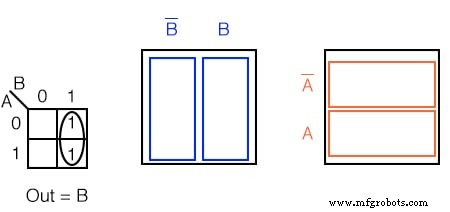
解決策:
隣接するセル、つまりセルの上または横を探します。対角セルは隣接していません。隣接するセルには、共通の1つ以上のブール変数があります。
- 2つの 1 をグループ化(丸で囲みます) s列に
- グループで同じ変数topおよび/またはsideを見つけ、これをブール結果として書き込みます。 B 私たちの場合。
- セルグループで同じではない変数を無視します。この場合、Aは変化し、1と0の両方であり、ブールAを無視します。
- 1を含むセルに関連付けられていない変数は無視してください。 B ’ その下には誰もいません。 Bを無視する
- 結果 Out =B
これは、右側のベン図、特に B と比較すると、見やすくなる可能性があります。 列。
例:
以下のカルノー図のブール式を記述します。
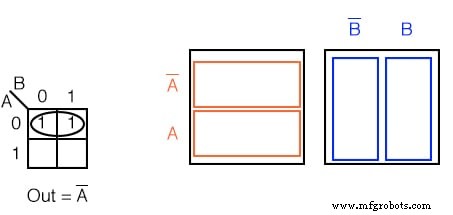
解決策: (上)
- 2つの 1をグループ化(丸で囲みます) 行に
- グループで同じ変数を見つけます。 Out =A ’
例:
以下の真理値表では、出力をKarnaughに転送してから、結果のブール式を記述します。
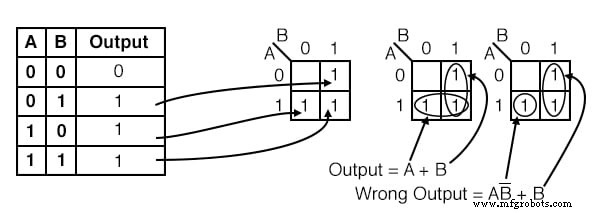
解決策:
1 を転送します ■真理値表の場所からKマップの対応する場所へ。
- B =1 の下の列にある2つの1をグループ化(丸で囲みます)
- A =1 の右側の行にある2つの1をグループ化(円)します
- 最初のグループの製品用語を書く= B
- 2番目のグループの製品用語を書く= A
- 上記の2つの項の総和を書く出力=A + B
真ん中のK-mapのソリューションは、最も単純または最も低コストのソリューションです。あまり望ましくない解決策は右端にあります。 2つをグループ化した後 1 s、1セルのグループを形成するという間違いを犯します。これが望ましくない理由は次のとおりです。
- 単一セルの製品用語は AB ’
- 対応するソリューションは出力=AB ’+ B
- これは最も簡単な解決策ではありません
このシングルを手に入れる方法 1 1 で2つのグループを形成することです この 1 にもかかわらず、中央のKマップの下の行に示されているようにその右側にあります すでに列グループに含まれています( B )。より大きなグループを形成するために、セルを再利用することが許可されています。実際、より単純な結果につながるため、望ましいです。
上記の解決策のいずれか、出力または間違った出力が論理的に正しいことを指摘する必要があります。どちらの回路も同じ出力を生成します。前者の回路が最も低コストのソリューションであることが問題です。
例:
以下のブール式のカルノー図に入力してから、結果のブール式を記述します。
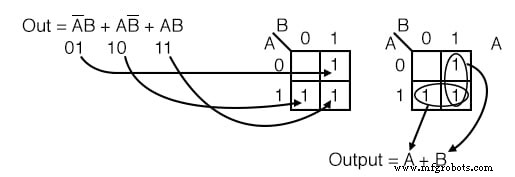
解決策: (上)
ブール式には3つの積項があります。 1 があります 製品用語ごとに入力します。ただし、一般的に、 1 の数は s製品用語ごとは、Kマップのサイズと比較した製品用語の変数の数によって異なります。
製品用語は、 1 が存在するセルのアドレスです。 入力されます。最初の製品用語、 A’B 、 01 に対応します マップ内のセル。 1 このセルに入力されます。他の2つのP項は、合計3つの 1 で入力されます。
次に、前の真理値表の問題と同様に、簡略化された結果のグループ化と抽出に進みます。
例:
以下の論理図を簡略化してください。
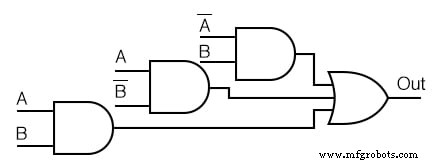
解決策: (下の図)
- 以下に示すように、元の論理図のブール式を記述します
- 製品用語をカルノー図に転送します
- 前の例のようにセルのグループを形成する
- 前の例のようにグループのブール式を記述します
- 簡略化された論理図を描く
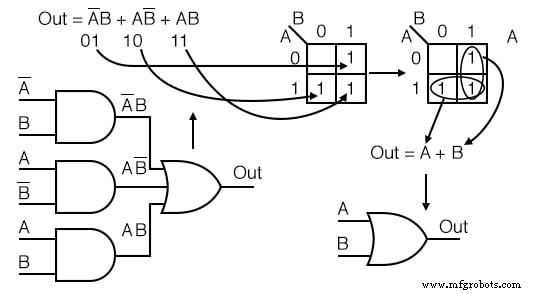
例: 以下の論理図を簡略化してください。
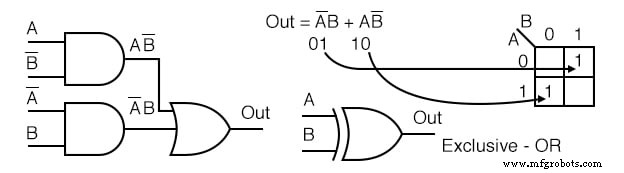
解決策:
- 上記の元の論理図のブール式を記述します
- 製品用語をカルノー図に転送します。
- グループを形成することはできません。
- 単純化することはできません。そのままにしておきます。
上記の図では、論理を単純化することはできません。これは時々起こります。カルノー図の方法もブール代数の方法も、この論理をさらに単純化することはできません。
上に排他的論理和の回路図記号を示します。ただし、これは論理的な単純化ではありません。スケマティックダイアグラムの見栄えを良くするだけです。
排他的論理和ロジックを単純化することは不可能であり、広く使用されているため、基本的な集積回路(7486)としてメーカーから提供されています。
関連するワークシート:
- カルノーマッピングワークシート
- ブール代数ワークシート
- 基本的な論理ゲートワークシート
産業技術



