コンポーネント障害分析（続き）

「次の場合に方程式を理解していると思います実際に解くことなく、その解の特性を予測することができます。」 —P.A.Mディラック、物理学者

ディラックからのその引用には多くの真実があります。少し変更を加えるだけで、「実際に計算を行わなくても、回路に加えられたさまざまな変更のおおよその影響を予測できれば、回路を理解できたと思います」と言うことで、彼の知恵を電気回路にまで広げることができます。

直列および並列回路の章の最後で、回路を定性的で分析する方法について簡単に検討しました。 定量的ではなく マナー。このスキルを身に付けることは、電気回路の熟練したトラブルシューティングを行うための重要なステップです。特定の障害が回路にどのように影響するかを完全に理解すると（つまり、結果を予測するために演算を実行する必要がない）、逆の方法で作業するのがはるかに簡単になります。回路がどのように動作しているかを評価します。

また、直列および並列回路の章の最後に、正常な回路の分析と同様に、障害分析を支援するためにテーブル方式がどのように機能するかを示しました。この手法をさらに一歩進めて、総合的な定性分析に適応させることができます。 「定性的」 正確な数字ではなく、「増加」、「減少」、「同じ」を表す記号を使用することを意味します。

直列回路と並列回路の原理、およびオームの法則の概念を引き続き使用できます。シンボリックな品質を使用します 数値の数量の代わりに 。これを行うことで、抽象的な方程式に頼るのではなく、回路がどのように機能するかについてより直感的な「感覚」を得ることができ、ディラックの「理解」の定義を達成できます。

複雑な回路のコンポーネント障害分析

十分な話。この手法を実際の回路例で試して、どのように機能するかを見てみましょう。

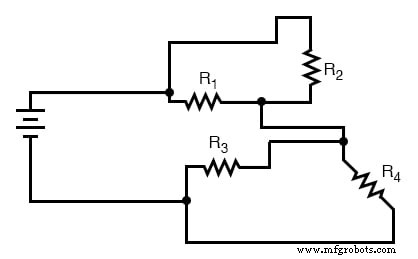
これは、前のセクションで分析のためにまっすぐにした最初の「複雑な」回路です。この特定の回路がどのように直列セクションと並列セクションに還元されるかをすでに知っているので、プロセスをスキップして、最終的な形式に直接進みます。

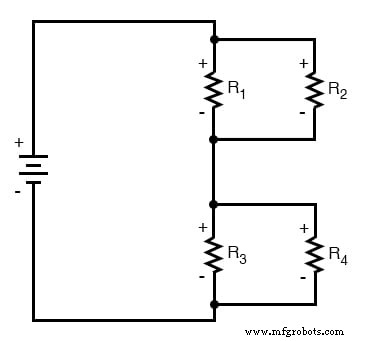
R ₃ およびR ₄ 互いに並列です。 R ₁ もそうです およびR ₂ 。 R ₃ の並列等価物 // R ₄ およびR ₁ // R ₂ 互いに直列です。記号で表すと、この回路の総抵抗は次のようになります。

R _合計 =（R ₁ // R ₂ ）—（r ₃ // R ₄ ）

まず、この回路に必要なすべての行と列を含むテーブルを作成する必要があります。

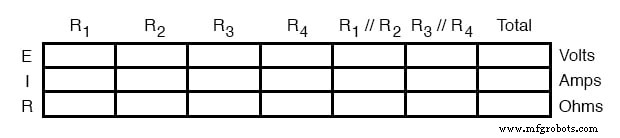
障害シナリオの分析

次に、障害シナリオが必要です。抵抗R ₂ ショートに失敗することになっていました。他のすべてのコンポーネントは元の値を維持していると想定します。この回路を定量的ではなく定性的に分析するため、テーブルに実数を挿入することはありません。

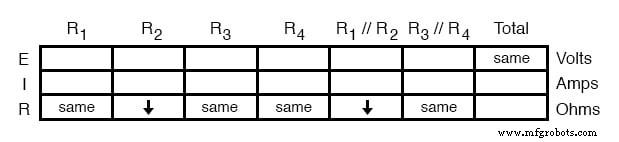
コンポーネントの故障後に変更されていない数量については、「以前からの変更なし」を表すために「同じ」という言葉を使用します。失敗の結果として変更された数量については、「減少」には下向き矢印を使用し、「増加」には上向き矢印を使用します。

いつものように、私たちは個々の抵抗と合計電圧、私たちの「与えられた」値のためにテーブルのスペースを埋めることから始めます：

回路の通常の状態とは異なる唯一の「与えられた」値はR ₂ です。 、私たちが言ったように、短絡に失敗しました（異常に低い抵抗）。他のすべての初期値は、「同じ」エントリで表されるように、以前と同じです。今やらなければならないのは、おなじみのオームの法則と直並列の原理を調べて、他のすべての回路値に何が起こるかを判断することです。

まず、並列サブセクションR ₁ の抵抗がどうなるかを判断する必要があります。 // R ₂ およびR ₃ // R ₄ 。どちらでもない場合R ₃ また、R ₄ 抵抗値が変化した場合、それらの並列の組み合わせも変化しません。

ただし、R ₂ の抵抗のため R ₁ の間、減少しました 同じままである場合、それらの並列の組み合わせも抵抗を減らす必要があります：

ここで、総抵抗がどうなるかを理解する必要があります。この部分は簡単です。回路内の1つのコンポーネントの変更のみを処理する場合、総抵抗の変化は、故障したコンポーネントの変化と同じ方向になります。これは、マグニチュードということではありません 個々のコンポーネントと回路全体の間の変化は同じであり、方向だけです。 変化の。つまり、単一の抵抗の値が減少すると、回路全体の抵抗も減少する必要があり、その逆も同様です。

この場合、R ₂ 故障した唯一のコンポーネントであり、その抵抗が減少しているため、総抵抗は必須 減少：

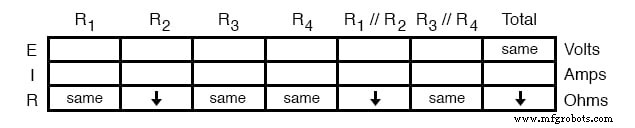
これで、オームの法則を（定性的に）テーブルの[合計]列に適用できます。全電圧が同じままで全抵抗が減少しているという事実を考えると、全電流を増加させる必要があると結論付けることができます（I =E / R）。

障害分析におけるオームの法則の定性的評価の使用

方程式の定性的評価に慣れていない場合は、次のように機能します。まず、未知の量を解く方程式を書きます。この場合、与えられた電圧と抵抗で電流を解こうとしています：

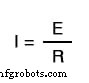
方程式が適切な形式になっているので、「E」と「R」への変更を前提として、「I」がどのような変更を経験するかを評価します。

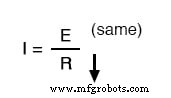
分数の分母の値が減少し、分子が同じままの場合、分数の全体的な値は増加する必要があります。

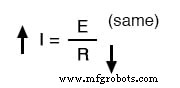
したがって、オームの法則（I =E / R）は、電流（I）が増加することを示しています。表でこの結論を「上」矢印でマークします：

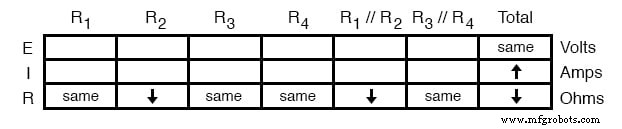
表にすべての抵抗の場所が記入され、[合計]列ですべての数量が決定されたら、他の電圧と電流の決定に進むことができます。この表の総抵抗がR ₁ の結果であることを知っています。 // R ₂ およびR ₃ // R ₄ シリーズ 、合計電流の値はR ₁ の値と同じになることがわかっています。 // R ₂ およびR ₃ // R ₄ （直列コンポーネントは同じ電流を共有するため）

したがって、総電流が増加した場合、R ₁ を流れる電流 // R ₂ およびR ₃ // R ₄ R ₂ の失敗で増加したに違いありません ：

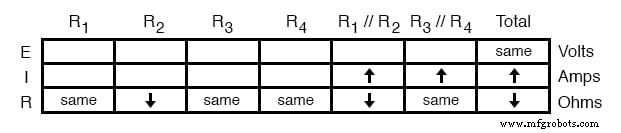
基本的に、オームの法則と直列および並列回路の規則を定性的に使用してここで行っていることは、数値で以前に行ったことと同じです。実際、計算で算術や電卓のキーストロークエラーが発生することを心配する必要がないため、はるかに簡単です。代わりに、原則に焦点を当てているだけです。 方程式の背後にあります。

上記の表から、オームの法則がR ₁ に適用されるはずであることがわかります。 // R ₂ およびR ₃ // R ₄ 列。 R ₃ の場合 // R ₄ 、電流が増加し、抵抗が変化しない場合、電圧がどうなるかを計算します。直感的には、これにより、R ₃ の並列組み合わせの両端の電圧が上昇する必要があることがわかります。 // R ₄ ：

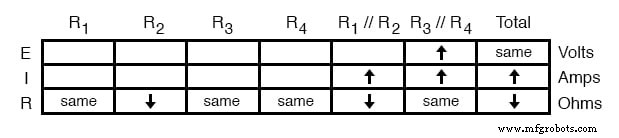
障害分析での回路分析ルールの使用

しかし、同じオームの法則の式（E =IR）をR ₁ にどのように適用するのでしょうか。 // R ₂ 抵抗が減少する列および 電流が増加していますか？ R ₃ の場合のように、1つの変数だけが変更されているかどうかを簡単に判断できます。 // R ₄ 、しかし、2つの変数が動き回っていて、使用できる明確な数値がないため、オームの法則はあまり役に立ちません。

ただし、水平に適用できる別のルールがあります R ₁ の両端の電圧がどうなるかを判断する // R ₂ ：直列回路の電圧の規則。 R ₁ の両端の電圧の場合 // R ₂ およびR ₃ // R ₄ 合計すると、合計（バッテリー）電圧に等しくなり、R ₃ // R ₄ 合計電圧が同じままで電圧が上昇した後、R ₁ の両端の電圧 // R ₂ 必須 R ₂ の変更に伴い減少しています の抵抗値：

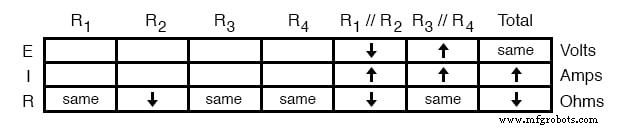
これで、テーブルのいくつかの新しい列に進む準備ができました。そのR ₃ を知っている およびR ₄ 並列サブセクションR ₃ を構成します // R ₄ 、および電圧が並列コンポーネント間で均等に共有されることを知っていると、並列の組み合わせR ₃ 全体で見られる電圧の増加 // R ₄ R ₃ 全体にも表示される必要があります およびR ₄ 個別に：

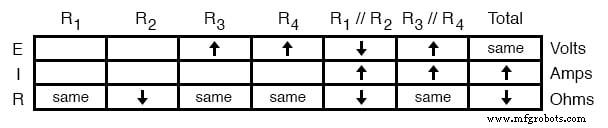
同じことがR ₁ にも当てはまります およびR ₂ 。 R ₁ の並列組み合わせで見られる電圧低下 およびR ₂ R ₁ 全体に表示されます およびR ₂ 個別に：

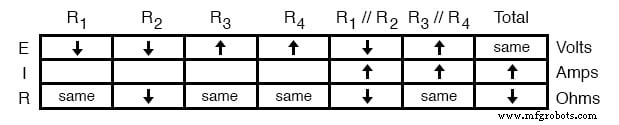
抵抗値が変更されていない（「同じ」）列にオームの法則を垂直に適用すると、これらのコンポーネントを流れる電流がどうなるかがわかります。変化しない抵抗の両端の電圧が上昇すると、電流が増加します。逆に、変化しない抵抗の両端の電圧が低下すると、電流が低下します。

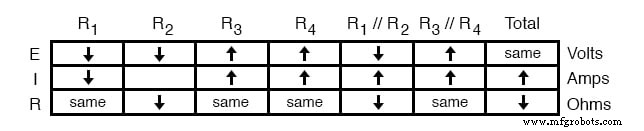
もう一度、オームの法則が私たちを助けることができない位置にいることに気づきます：R ₂ 、電圧と抵抗の両方が減少しましたが、どのくらいかはわかりません。 それぞれが変更されているため、I =E / Rの式を使用して、結果として生じる電流の変化を定性的に判断することはできません。ただし、直列および並列回路のルールを水平に適用することはできます。 。 R ₁ を流れる電流は // R ₂ 並列の組み合わせが増えており、R ₁ を流れる電流もわかっています。 減少しました。

並列回路のルールの1つは、合計電流が個々の分岐電流の合計に等しいということです。この場合、R ₁ を流れる電流 // R ₂ R ₁ を流れる電流に等しい R ₂ を流れる電流に追加 。 R ₁ を流れる場合 // R ₂ R ₁ を流れる電流が増加している 減少しました、R ₂ を流れる電流 必須 増加しました：

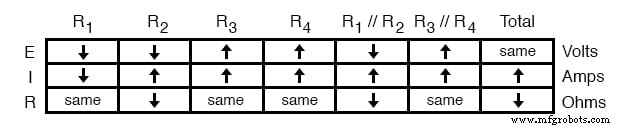
これで、定性的価値の表が完成しました。この特定の演習は、すべての詳細な解説のために面倒に見えるかもしれませんが、実際のプロセスは、いくつかの練習で非常に迅速に実行できます。ここで理解しておくべき重要なことは、一般的な手順が定量分析と少し異なることです。既知の値から始めて、次に総抵抗、次に総電流を決定し、次に直列の規則で許可されているように電圧と電流の数値を転送します。適切な列への並列回路。

このような分析を進める際に、進捗状況を支援および/または確認するために、いくつかの一般的なルールを覚えておくことができます。

• 任意のシングル コンポーネントの故障（オープンまたはショート）の場合、合計抵抗は、故障したコンポーネントの抵抗の変化と常に同じ方向（増加または減少）に変化します。
• コンポーネントの短絡が失敗すると、その抵抗は常に減少します。また、それを流れる電流が増加し、その両端の電圧が 落とす。場合によっては同じままであるため、「可能性があります」と言います（適切な例：理想的な電源を備えた単純な並列回路）。
• コンポーネントがフェールオープンすると、その抵抗は常に増加します。そのコンポーネントを流れる電流は、不完全な電気経路（導通なし）であるため、ゼロに減少します。このかもしれません その結果、両端の電圧が上昇します。上記と同じ例外がここでも当てはまります。理想的な電圧源を備えた単純な並列回路では、オープン障害のあるコンポーネントの両端の電圧は変化しません。

関連するワークシート：

• シリーズ-並列DC回路ワークシート