ノード電圧法

解析のノード電圧法は、KCL方程式のシステムの観点から回路ノードの未知の電圧を解決します。この分析は、電圧源を同等の電流源に置き換える必要があるため、奇妙に見えます。また、オーム単位の抵抗値は、ジーメンス単位の等価コンダクタンスG =1 / Rに置き換えられます。ジーメンス（S）はコンダクタンスの単位であり、モー単位に取って代わりました。いずれにせよ、S =Ω-1。そして、S =mho（廃止）。

ノード電圧の計算方法

まず、従来の電圧源を備えた回路から始めます。共通ノードE ₀ 基準点として選択されます。ノード電圧E ₁ およびE ₂ この点に関して計算されます。

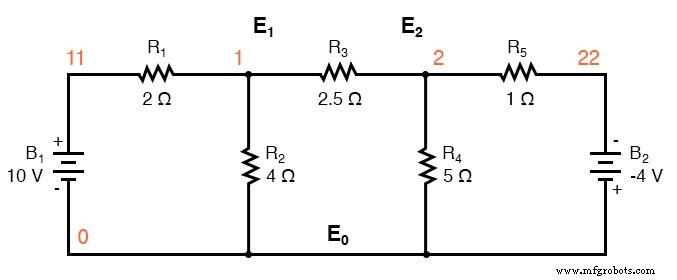
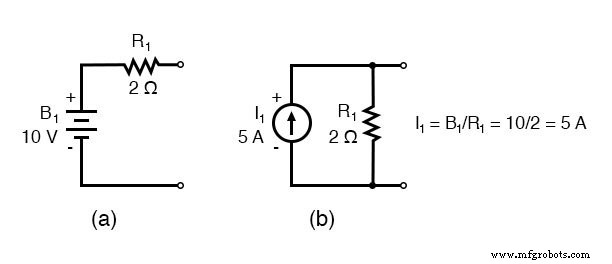
電圧源と関連する直列抵抗を同等の電流源と並列抵抗に置き換えると、回路が変更されます。オーム単位の抵抗をジーメンス単位の抵抗コンダクタンスに置き換えます。

 I1 =E1 / R1 =10/2 =5 A I2 =E2 / R5 =4/1 =4 A G1 =1 / R1 =1 /2Ω=0.5 S G2 =1 / R2 =1 /4Ω=0.25 S G3 =1 / R3 =1/2.5Ω=0.4 S G4 =1 / R4 =1 /5Ω=0.2 S G5 =1 / R5 =1 /1Ω=1.0 S 

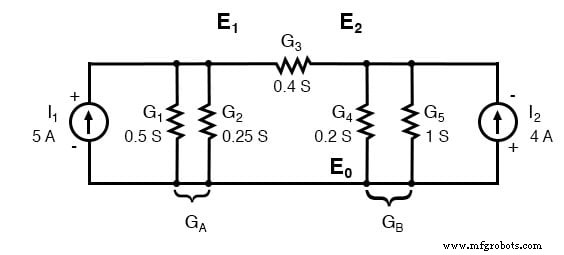
並列コンダクタンス（抵抗）は、コンダクタンスを追加することで組み合わせることができます。ただし、回路を再描画することはありません。回路はノード電圧法を適用する準備ができています。

 GA =G1 + G2 =0.5 S + 0.25 S =0.75 S GB =G4 + G5 =0.2 S + 1 S =1.2 S 

一般的なノード電圧法を導き出し、未知のノード電圧V ₁ に関してKCL方程式のペアを記述します。 およびV ₂ 今回は。これは、検査によって方程式を書くためのパターンを説明するために行います。

 GAE1 + G3（E1-E2）=I1（1） GBE2-G3（E1-E2）=I2（2） （GA + G3）E1 -G3E2 =I1（1） -G3E1 +（GB + G3）E2 =I2（2） 

上記の方程式の最後のペアの係数は、パターンを示すために再配置されています。最初のノードに接続されているコンダクタンスの合計は、式（1）の最初の電圧の正の係数です。 2番目のノードに接続されているコンダクタンスの合計は、式（2）の2番目の電圧の正の係数です。他の係数は負であり、ノード間のコンダクタンスを表します。どちらの式でも、右辺はノードに接続されているそれぞれの電流源に等しくなります。このパターンにより、検査によって方程式をすばやく書くことができます。これにより、ノード電圧の分析方法に関する一連のルールが導き出されます。

ノード電圧ルール：

• 抵抗器と直列の電圧源を、抵抗器が並列の同等の電流源に変換します。
• 抵抗値をコンダクタンスに変更します。
• 参照ノードを選択します（E ₀ ）
• 未知の電圧を割り当てます（E ₁ ）（E ₂ ）...（E _N ）残りのノードに。
• ノード1、2、... NごとにKCL方程式を記述します。最初の方程式の最初の電圧の正の係数は、ノードに接続されているコンダクタンスの合計です。 2番目の式の2番目の電圧の係数は、そのノードに接続されているコンダクタンスの合計です。 3番目の電圧の係数、3番目の方程式、およびその他の方程式について繰り返します。これらの係数は対角線上にあります。
• すべての方程式の他のすべての係数は負であり、ノード間のコンダクタンスを表します。最初の方程式、2番目の係数はノード1からノード2までのコンダクタンス、3番目の係数はノード1からノード3までのコンダクタンスです。他の方程式には負の係数を入力します。
• 方程式の右辺は、それぞれのノードに接続されている電流源です。
• 未知のノード電圧の連立方程式を解きます。

ノード電圧法の例

例： 方程式を設定し、上の図の数値を使用してノード電圧を解きます。

解決策：

 （0.5 + 0.25 + 0.4）E1-（0.4）E2 =5 -（0.4）E1 +（0.4 + 0.2 + 1.0）E2 =-4 （1.15）E1-（0.4）E2 =5 -（0.4）E1 +（1.6）E2 =-4 E1 =3.8095 E2 =-1.5476 

2つの方程式の解は、電卓またはオクターブ（図示せず）を使用して実行できます。解決策は、電圧源を備えた元の概略図に基づいてSPICEで検証されます。ただし、電流源を使用した回路をシミュレートすることもできます。

 V1 11 0 DC 10 V2 22 0 DC -4 r1 11 1 2 r2 1 0 4 r3 1 2 2.5 r4 2 0 5 r5 2 22 1 .DC V1 10 10 1 V2 -4 -4 1 .print DC V（1）V（2） 。終わり v（1）v（2） 3.809524e + 00 -1.547619e + 00 

もう1つの例。これには3つのノードがあります。概略図にはコンダクタンスは記載されていません。ただし、G ₁ =1 / R ₁ 、など。

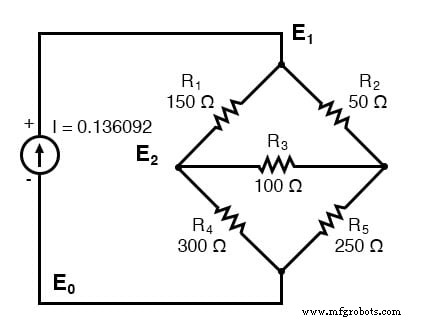
検査によって方程式を書くための3つのノードがあります。式（1）E ₁ の係数は正であることに注意してください。 、式（2）E ₂ 、および式（3）E ₃ 。これらは、ノードに接続されているすべてのコンダクタンスの合計です。他のすべての係数は負であり、ノード間のコンダクタンスを表します。方程式の右辺は関連する電流源であり、ノード1の唯一の電流源の場合は0.136092 Aです。他の方程式は、電流源がないため右辺がゼロです。怠惰すぎて、図の抵抗器のコンダクタンスを計算できません。したがって、下付きのGは係数です。

（G1 + G2）E1 -G1E2 -G2E3 =0.136092 -G1E1 +（G1 + G3 + G4）E2 -G3E3 =0 -G2E1 -G3E2 +（G2 + G3 + G5）E3 =0 

私たちは非常に怠惰なので、オクターブ「A」マトリックスに逆数抵抗と逆数抵抗の合計を入力し、オクターブに「A =」の後のコンダクタンスのマトリックスを計算させます。最初のエントリ行は非常に長いため、3行に分割されました。これは前の例とは異なります。入力された「A」マトリックスは、開始および終了の角括弧で表されます。列要素はスペースで区切られています。行は「改行」で区切られます。区切り文字としてコンマとセミコロンは必要ありません。ただし、「b」の電流ベクトルはセミコロンで区切られ、電流の列ベクトルが生成されます。

 オクターブ：12> A =[1/150 + 1/50 -1/150 -1/50> -1/150 1/150 + 1/100 + 1/300 -1/100> -1/50 -1/100 1/50 + 1/100 + 1/250] A =0.0266667 -0.0066667 -0.0200000 -0.0066667 0.0200000 -0.0100000 -0.0200000 -0.0100000 0.0340000 オクターブ：13> b =[0.136092; 0; 0] b =0.13609 0.00000 0.00000 オクターブ：14> x =A \ b x =24.000 17.655 19.310 

「A」行列の対角係数は正であり、他のすべての係数は負であることに注意してください。

電圧ベクトルとしての解は「x」にあります。 E ₁ =24.000 V、E ₂ =17.655 V、E ₃ =19.310V。これらの3つの電圧は、不平衡ブリッジ問題に対する以前のメッシュ電流およびSPICEソリューションと比較されます。これは偶然ではありません。0.13609Aの電流源は、その問題で電圧源として使用される24Vを生成するために意図的に選択されました。

概要

• コンダクタンスと電流源のネットワークが与えられると、回路解析のノード電圧法は、KCL方程式から未知のノード電圧を解決します。
• 検査による方程式の記述の詳細については、上記のルールを参照してください。
• コンダクタンスの単位GはジーメンスSです。コンダクタンスは抵抗の逆数です：G =1 / R

関連するワークシート：

• 正確なダイオード回路ワークシート
• キルヒホッフの法則ワークシート