電圧と電流の計算

時間の経過に伴う無効DC回路の値を計算する確実な方法があります。

リアクティブDC回路の値の計算

最初のステップは、コンデンサまたはインダクタが変化に対抗する量の開始値と最終値を特定することです。つまり、反応性成分が一定に保とうとしている量が何であれ。コンデンサの場合、この量は電圧です。;インダクタの場合、この量は電流 。回路内のスイッチが閉じている（または開いている）と、リアクティブコンポーネントはその量をスイッチ遷移前と同じレベルに維持しようとするため、値は「開始」値に使用されます。

この数量の最終的な値は、無限の時間が経過した後の数量になります。これは、コンデンサが開回路であるかのように容量回路を分析し、インダクタが短絡であるかのように誘導回路を分析することで判断できます。これは、これらのコンポーネントが「フル充電」に達したときの動作であるためです。無限の時間の後。

次のステップは、時定数を計算することです。 回路の：過渡状態で電圧または電流値が開始値から最終値まで約63％変化するのにかかる時間。

直列RC回路では、時定数はオーム単位の総抵抗にファラッド単位の総静電容量を掛けたものに等しくなります。直列L / R回路の場合、これはヘンリーの総インダクタンスをオームの総抵抗で割ったものです。いずれの場合も、時定数は秒の単位で表されます。 ギリシャ文字の「タウ」（τ）で象徴されています：

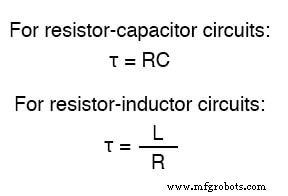
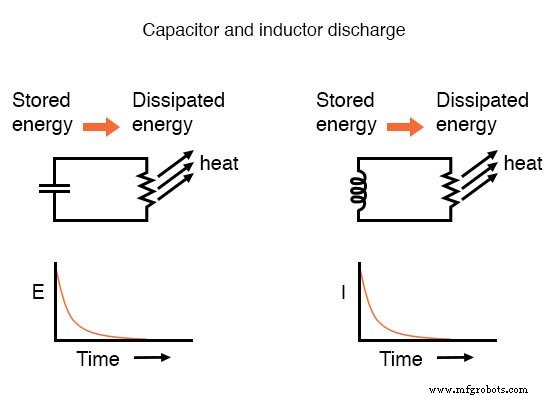
過渡応答に応じた電圧や電流などの回路値の上昇と下降は、前述のように、漸近的 。そのため、値はトランジェントの直後に急速に変化し始め、時間の経過とともに落ち着きます。グラフにプロットすると、電圧と電流の最終値へのアプローチが指数曲線を形成します。

前に述べたように、1つの時定数は、これらの値のいずれかが開始値から（最終的な）最終値まで約63％変化するのにかかる時間です。時定数ごとに、これらの値は（約）63％最終目標に近づきます。正確なパーセンテージを決定するための数式は非常に単純です：

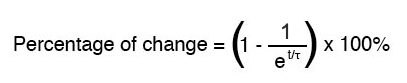
手紙 e オイラーの定数を表し、約2.7182818です。これは、回路値の漸近的アプローチを数学的に分析した後、微積分技術から導き出されます。 1回の時定数に相当する時間の後、開始値から最終値への変化のパーセンテージは次のようになります。

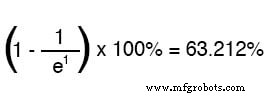
2つの時定数に相当する時間の後、開始値から最終値への変化のパーセンテージは次のとおりです。

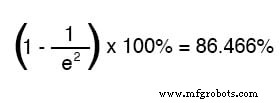
10時定数に相当する時間の後、パーセンテージは次のようになります。

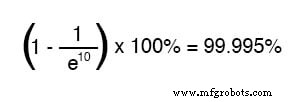
バッテリーからの一時的な電圧の印加から経過する時間が長いほど、分数の分母の値が大きくなり、分数全体の値が小さくなり、総計（1から分数を引いたもの）が近づきます。 1、または100パーセント。

ユニバーサル時定数式

この量に最終回路値と開始回路値の差を掛けることにより、過渡回路の電圧と電流の値を決定するために、これからより普遍的な式を作成できます。

この章の冒頭に示した直列抵抗-コンデンサ回路の電圧上昇を分析してみましょう。

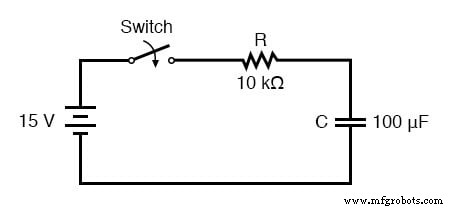
電圧を分析することを選択していることに注意してください。これは、コンデンサが一定に保たれる傾向があるためです。この式は電流に対して非常にうまく機能しますが、電流の開始値と最終値は実際にはコンデンサの電圧から導出されるため、電圧の計算はより直接的な方法です。抵抗は10kΩ、静電容量は100 µF（マイクロファラッド）です。 RC回路の時定数（τ）は抵抗と静電容量の積であるため、1秒の値が得られます。

コンデンサが完全に放電された状態（0ボルト）で始動する場合、その電圧値を「始動」値として使用できます。もちろん、最終的な値はバッテリー電圧（15ボルト）になります。この回路のコンデンサ電圧の普遍的な式は次のようになります：

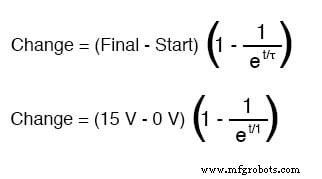
したがって、閉じたスイッチを介して7.25秒間電圧を印加した後、コンデンサの電圧は次のように増加します。

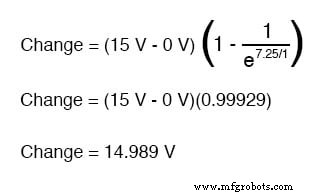
0ボルトのコンデンサ電圧で開始したので、この14.989ボルトの増加は、7.25秒後に14.989ボルトになることを意味します。

同じ式は、その回路の電流を決定するためにも機能します。放電したコンデンサは最初は短絡のように機能することがわかっているので、開始電流は可能な最大量になります：15ボルト（バッテリーから）を10kΩで割ったもの（最初の回路の電流に対する唯一の反対）：

また、コンデンサは最終的に開回路として動作するため、最終的な電流はゼロになることもわかっています。つまり、最終的には電子が回路に流れなくなります。開始電流値と最終電流値の両方がわかったので、ユニバーサル式を使用して、同じRC回路で7.25秒のスイッチを閉じた後の電流を決定できます。

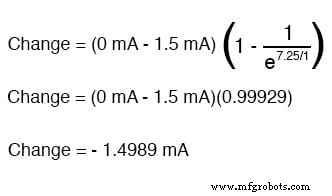
変更のために得られた数値は、正ではなく負であることに注意してください。これは、電流が減少したことを示しています。 時間の経過とともに増加するのではなく。 1.5 mAの電流で開始したため、この減少（-1.4989 mA）は、7.25秒後に0.001065 mA（1.065 µA）になることを意味します。

また、バッテリーの電圧（15ボルト）からコンデンサの電圧（14.989ボルト）を差し引いて10kΩの抵抗器の両端の電圧降下を求め、抵抗器（およびオームの法則（I =E / R）を使用した直列回路全体）。いずれにせよ、同じ答えを得る必要があります：

誘導回路の分析にユニバーサル時定数式を使用する

普遍的な時定数の式は、誘導回路の分析にも適しています。この章の冒頭にあるL / R回路の例に適用してみましょう。

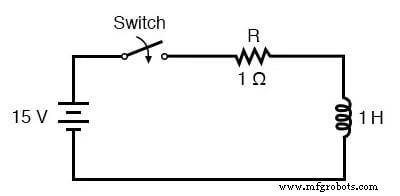
インダクタンスが1ヘンリー、直列抵抗が1Ωの場合、時定数は1秒に等しくなります。

これは誘導回路であり、インダクタが電流の変化に対抗することがわかっているため、電流の開始値と最終値の時定数式を設定します。スイッチを開いた位置から開始すると、電流はゼロに等しくなるため、ゼロが開始電流値になります。

スイッチを長時間閉じたままにすると、電流は最終値に落ち着きます。これは、電源電圧を回路の総抵抗（I =E / R）で割った値、またはこの回路の場合は15アンペアに等しくなります。 。

3.5秒での電流の値を決定したい場合は、次のようなユニバーサル時定数式を適用します。

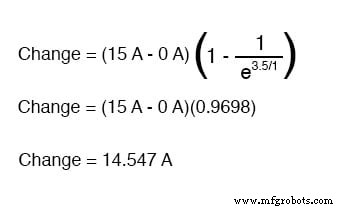
開始電流がゼロであるという事実を考えると、これにより、3.5秒の時点で14.547アンペアの回路電流が残ります。

誘導回路の電圧を決定するには、最初に回路電流を計算し、次に抵抗の両端の電圧降下を計算して、インダクタの両端の電圧降下を見つけるのが最適です。この例の回路には抵抗が1つしかないため（値は1Ω）、これはかなり簡単です。

15ボルトのバッテリー電圧から差し引くと、時間=3.5秒でインダクターの両端に0.453ボルトが残ります。

レビュー：

• ユニバーサル時定数式：
• RCまたはL / R回路を分析するには、次の手順に従います。
• （1）：回路の時定数（RCまたはL / R）を決定します。
• （2）：計算する量を特定します（その変化が無効成分によって直接反対される量。コンデンサの場合は電圧、インダクタの場合は電流）。
• （3）：その数量の開始値と最終値を決定します。
• （4）：これらすべての値（最終、開始、時間、時定数）をユニバーサル時定数の式に代入し、変更を解きます。 量的に。
• （5）：開始値がゼロの場合、指定された時間の実際の値は、ユニバーサル式によって与えられた計算された変化に等しくなります。そうでない場合は、開始値に変更を追加して、現在の場所を確認します。

関連するワークシート：

• 時定数回路ワークシート
• 時定数計算ワークシート

コレクションを表示 電力計算機 私たちの ツール セクション。