ACマグニチュードの測定

これまでのところ、AC電圧は極性が交互になり、AC電流は方向が交互になることがわかっています。また、ACはさまざまな方法で交互に変化する可能性があることもわかっています。時間の経過とともに変化を追跡することで、ACを「波形」としてプロットできます。

波が繰り返されるまでにかかる時間（「周期」）を測定することで交代率を測定し、これを単位時間あたりのサイクル数または「周波数」として表すことができます。音楽では、頻度はピッチと同じです。 、これは、ある音符を別の音符と区別するための重要なプロパティです。

しかし、AC量の大小を表現しようとすると、測定の問題が発生します。電圧と電流の量が一般的に安定しているDCでは、回路の任意の部分にある電圧または電流の量を表現するのにほとんど問題はありません。

しかし、絶えず変化しているものに、どのようにして単一の大きさの測定値を与えるのですか？

AC波形の大きさを表現する方法

強度または大きさを表す1つの方法（振幅とも呼ばれます） ）、AC量のは、波形グラフでそのピーク高さを測定することです。これはピークとして知られています またはクレスト AC波形の値：下の図

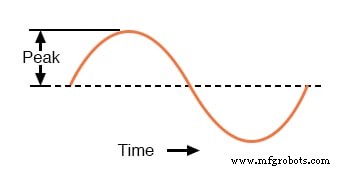
波形のピーク電圧。

もう1つの方法は、反対側のピーク間の全高を測定することです。これは、ピークツーピークとして知られています。 （P-P）AC波形の値：下の図

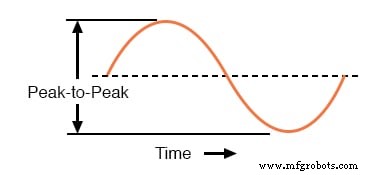
波形のピークツーピーク電圧。

残念ながら、これらの波形振幅の表現のいずれかは、2つの異なるタイプの波を比較するときに誤解を招く可能性があります。たとえば、10ボルトでピークに達する方形波は、10ボルトでピークに達する三角波よりも、明らかに長時間にわたってより多くの電圧になります。

負荷に電力を供給するこれらの2つのAC電圧の影響は、まったく異なります。下の図

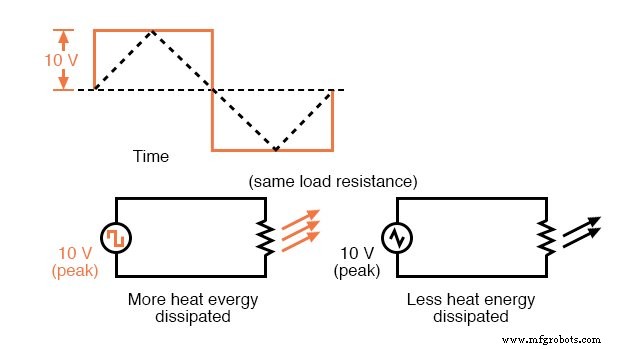
方形波は、同じピーク電圧の三角波よりも大きな加熱効果を生み出します。

さまざまな波形の振幅をより同等の方法で表現する1つの方法は、波形のグラフ上のすべてのポイントの値を数学的に平均して、単一の集計数にすることです。この振幅測定は、単に平均として知られています。 波形の値。

波形上のすべてのポイントを代数的に平均すると（つまり、それらの符号を考慮する場合） 、正または負のいずれか）、すべての正の点が全サイクルにわたってすべての負の点を相殺するため、ほとんどの波形の平均値は技術的にゼロです。下の図

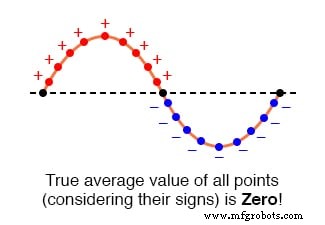
正弦波の平均値はゼロです。

もちろん、これは、プロットの「ゼロ」ラインの上下に等しい面積の部分があるすべての波形に当てはまります。ただし、実用的 波形の総計値の尺度である「平均」は、通常、すべてのポイントの絶対値の数学的平均として定義されます。 サイクル全体。

つまり、波形が次の​​ようになっているように、波形上のすべてのポイントを正の量と見なして、波形の実際の平均値を計算します。下の図

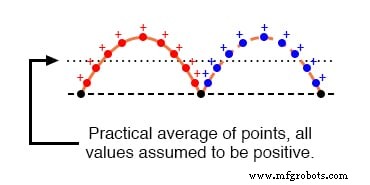
AC「平均応答」メーターで見た波形。

極性に影響されない機械的なメーターの動き（交流電圧または電流の正と負の半サイクルに等しく応答するように設計されたメーター）は、波形の（実際の）平均値に比例して記録されます。ばねは、時間の経過とともに変化する電圧/電流値によって生成される力を自然に平均化します。

逆に、極性に敏感なメーターの動きは、AC電圧または電流にさらされると無用に振動し、針はゼロマークを中心に急速に振動し、対称波形の真の（代数的）平均値ゼロを示します。このテキストで波形の「平均」値が参照されている場合、特に指定がない限り、平均の「実用的な」定義が意図されていると見なされます。

波形振幅の集計値を導出する別の方法は、負荷抵抗に適用されたときに有用な作業を行う波形の能力に基づいています。残念ながら、波形によって実行された作業に基づくAC測定は、電力のため、その波形の「平均」値と同じではありません。 与えられた負荷（単位時間あたりに実行される仕事）によって消費されるのは、それに加えられる電圧または電流の大きさに直接比例しません。

むしろ、パワーは二乗に比例します 抵抗器に印加される電圧または電流の割合（P =E ² / R、およびP =I ² R）。このような振幅測定の数学は簡単ではないかもしれませんが、その有用性は簡単です。

帯鋸とジグソー、2つの現代の木工設備を考えてみましょう。どちらのタイプの鋸も、薄い歯付きのモーター駆動の金属ブレードで切断して木材を切断します。しかし、帯鋸は刃の連続的な動きを使用して切断しますが、ジグソーは前後の動きを使用します。

交流（AC）と直流（DC）の比較は、これら2つの鋸タイプの比較に例えることができます。下の図

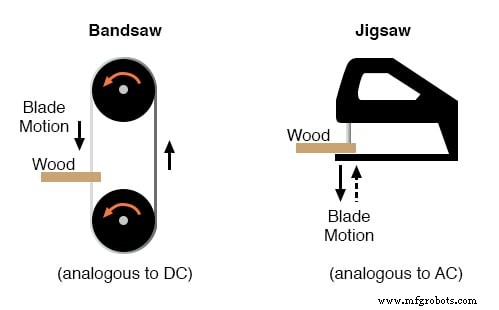
DCとACのバンドソー-ジグソーパズルのアナロジー。

単一の集計測定でAC電圧または電流の変化する量を記述しようとする問題は、この鋸のアナロジーにも存在します。ジグソーブレードの速度をどのように表現できるでしょうか。帯鋸刃は、DC電圧が押すのと同じように、またはDC電流が一定の大きさで移動するのと同じように、一定の速度で移動します。一方、ジグソーブレードは前後に動き、ブレードの速度は絶えず変化します。さらに、鋸の機械的設計によっては、2つのジグソーの前後の動きが同じタイプではない場合があります。

1つのジグソーは、正弦波の動きでブレードを動かし、別のジグソーは三角波の動きでブレードを動かす可能性があります。 ピークに基づいてジグソーを評価する あるジグソーを別のジグソー（またはバンドソー付きのジグソー！）と比較すると、ブレードの速度はかなり誤解を招く可能性があります。これらの異なる鋸は異なる方法でブレードを動かすという事実にもかかわらず、それらは1つの点で同等です。それらはすべて木材を切断し、この共通の機能の定量的比較は、ブレードの速度を評価するための共通の基礎として役立ちます。

>

同じブレード（同じ歯のピッチ、角度など）を備え、同じ種類の木材の同じ厚さを同じ速度で同じように切断できるジグソーとバンドソーを並べて想像してみてください。 2本ののこぎりは切断能力が同等か同等であったと言えます。この比較を使用して、「バンドソー相当」のブレード速度をジグソーの前後のブレードの動きに割り当てることができます。片方の木材伐採効果をもう一方に関連付けるには？

これは、任意のAC電圧または電流に「DC等価」測定値を割り当てるために使用される一般的な考え方です。DC電圧または電流の大きさに関係なく、等しい抵抗によって同じ量の熱エネルギー散逸が発生します。下の図

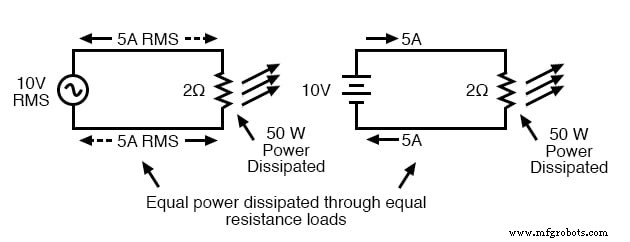
RMS電圧は、同じDC電圧と同じ加熱効果を生み出します

二乗平均平方根（RMS）はACとどのように関連していますか？

上記の2つの回路では、同じ量の負荷抵抗（2Ω）があり、1つはACから、もう1つはDCから電力を供給され、熱（50ワット）の形で同じ量の電力を消費します。上の写真のAC電圧源は、（負荷に供給される電力の点で）10ボルトのDCバッテリーと同等であるため、これを「10ボルト」のAC電源と呼びます。

より具体的には、その電圧値を10ボルト RMS と表記します。 。修飾子「RMS」は、二乗平均平方根の略です。 、グラフ上のポイントからDC等価値を取得するために使用されるアルゴリズム（基本的に、手順は、波形グラフ上のすべての正と負のポイントを2乗し、それらの2乗値を平均し、その平均の平方根を取得して、最終的な答え）。

時々、代替用語同等 または DC相当 「RMS」の代わりに使用されますが、量と原則はどちらも同じです。

RMS振幅測定は、電力の測定を行う場合に、AC量をDC量、またはさまざまな波形形状の他のAC量に関連付けるための最良の方法です。

その他の考慮事項については、ピークまたはピークツーピーク測定を採用するのが最適な場合があります。たとえば、電源から負荷に電力を送るためのワイヤの適切なサイズ（アンペア）を決定する場合、電流に関する主な懸念事項はワイヤの過熱であるため、RMS電流測定を使用するのが最適です。ワイヤの抵抗を流れる電流によって引き起こされる電力損失。

ただし、高電圧ACアプリケーションで使用するために絶縁体を評価する場合、ピーク電圧測定が最も適切です。これは、ここでの主な懸念事項は、時間に関係なく、電圧の短時間のスパイクによって引き起こされる絶縁体の「フラッシュオーバー」であるためです。

波形の振幅を測定するために使用される機器

ピークおよびピークツーピーク測定は、電圧の変化に応じたブラウン管の高速動作により、波形の山を高精度でキャプチャできるオシロスコープを使用して実行するのが最適です。 RMS測定の場合、アナログメーターの動き（ダーソンバル、ウェストン、鉄羽根、電気力計）は、RMS値で校正されている限り機能します。

電気機械式メーターの動きの機械的慣性と減衰効果により、針のたわみが自然に平均に比例するためです。 真のRMS値ではなく、ACの値であるアナログメーターは、電圧または電流をRMS単位で示すために、特別に校正する必要があります（または、見方によっては誤って校正する必要があります）。

このキャリブレーションの精度は、想定される波形、通常は正弦波に依存します。

RMS測定用に特別に設計された電子メーターがこのタスクに最適です。一部の機器メーカーは、任意の波形のRMS値を決定するための独創的な方法を設計しています。そのようなメーカーの1つは、測定されている電圧に比例した電圧で電力を供給される小さな抵抗発熱体を備えた「True-RMS」メーターを製造しています。

その抵抗要素の加熱効果を熱的に測定して、数学的な計算を一切行わずに真のRMS値を取得します。これは、RMSの定義を実現するための物理法則のみです。このタイプのRMS測定の精度は、波形に依存しません。

ピーク、ピークツーピーク、平均、およびRMSの関係

「純粋な」波形の場合、ピーク、ピークツーピーク、平均（実用的、代数的ではない）、およびRMS測定値を相互に等しくするための単純な変換係数が存在します。

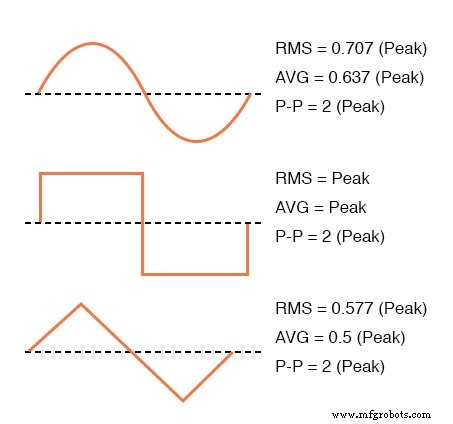
一般的な波形の変換係数。

AC波形のRMS、平均、ピーク（クレスト）、およびピークツーピークの測定値に加えて、これらの基本的な測定値のいくつかの間の比例関係を表す比率があります。 波高比 たとえば、AC波形の値は、ピーク（山）値をRMS値で割った比率です。

フォームファクター AC波形のは、そのRMS値をその平均値で割った比率です。正方形の波形は、ピークがRMSおよび平均値と同じであるため、常に1に等しい波高と形状係数を持ちます。正弦波形のRMS値は0.707（2の平方根の逆数）で、フォームファクターは1.11（0.707 / 0.636）です。

三角形とのこぎり波の波形のRMS値は0.577（3の平方根の逆数）で、フォームファクタは1.15（0.577 / 0.5）です。

ここに示されている正弦波、方形波、三角波のピーク、RMS、平均振幅の変換定数は、純粋なの場合にのみ当てはまることに注意してください。 これらの波形の形。歪んだ波形のRMS値と平均値は、同じ比率では関係ありません。下の図

任意波形には単純な変換はありません。

これは、AC電圧または電流を測定するためにアナログダルソンバルメータームーブメントを使用するときに理解するための非常に重要な概念です。正弦波のRMS振幅を示すように調整されたアナログのダルソンバル運動は、純粋な正弦波を測定する場合にのみ正確になります。

測定されている電圧または電流の波形が純粋な正弦波以外の場合、アナログのダルソンバルメーターの動きにおける針のたわみの程度は次のようになるため、メーターによって示される表示は波形の真のRMS値ではありません。 平均に比例します RMSではなく波形の値。

RMSメーターのキャリブレーションは、メーターのスパンを「スキュー」して、平均値の小さな倍数を表示することによって取得されます。これは、特定の波形および特定の波形のみのRMS値に等しくなります。 > 。

電気測定では正弦波形が最も一般的であるため、アナログメーターの校正で想定される波形であり、メーターの校正に使用される小倍数は1.1107です（フォームファクター：0.707 / 0.636：RMSの比率を除算したもの）正弦波の平均）。

純粋な正弦波以外の波形は、RMSと平均値の比率が異なるため、正弦波の電圧または電流に対して較正されたメーターは、非正弦波を読み取るときに真のRMSを示しません。この制限は、「True-RMS」テクノロジーを採用していない単純なアナログACメーターにのみ適用されることに注意してください。

レビュー：

• 振幅 AC波形の高さは、時間の経過に伴うグラフに示されている高さです。振幅測定は、ピーク、ピークツーピーク、平均、またはRMS量の形式をとることができます。
• ピーク 振幅は、ゼロマークからグラフの最高の正または最低の負のポイントまで測定されたAC波形の高さです。 クレストとも呼ばれます 波の振幅。
• ピークツーピーク 振幅は、グラフの最大の正のピークから最大の負のピークまで測定されたAC波形の全高です。多くの場合、「P-P」と略されます。
• 平均 振幅は、1サイクルの期間にわたるすべての波形のポイントの数学的「平均」です。技術的には、グラフの「ゼロ」線の上下に等しい面積の部分がある波形の平均振幅はゼロです。ただし、振幅の実際的な測定値として、波形の平均値は、多くの場合、すべてのポイントの絶対値の算術平均として計算されます。 （すべての負の値を取り、それらを正と見なします）。正弦波の場合、そのように計算された平均値は、そのピーク値の約0.637です。
• 「RMS」は二乗平均平方根の略です 、およびは、DCと機能的に同等の用語で電圧または電流のAC量を表す方法です。たとえば、10ボルトのAC RMSは、10ボルトのDC電源と同じ値の抵抗器の両端に同じ量の熱放散を生成する電圧の量です。 AC電圧または電流の「等価」または「DC等価」値とも呼ばれます。正弦波の場合、RMS値はピーク値の約0.707です。
• 波高比 AC波形の値は、RMS値に対するピーク（山）の比率です。
• フォームファクター AC波形の平均値に対するRMS値の比率です。
• アナログの電気機械式メーターの動きは、平均に比例して反応します。 AC電圧または電流の値。 RMS表示が必要な場合は、それに応じてメーターの校正を「ゆがめる」必要があります。これは、電気機械式メーターのRMS表示の精度が、波形の純度、つまり、校正に使用された波形とまったく同じ波形であるかどうかに依存することを意味します。

関連するワークシート：

• 基本的なオシロスコープ操作ワークシート