AC回路のいくつかの例

3つのAC電圧源を直列に接続し、複素数を使用して付加電圧を決定しましょう。

DC回路の研究で学んだすべての規則と法則は、電力計算（ジュールの法則）を除いて、AC回路にも適用されます（オームの法則、キルヒホッフの法則、ネットワーク分析方法）。

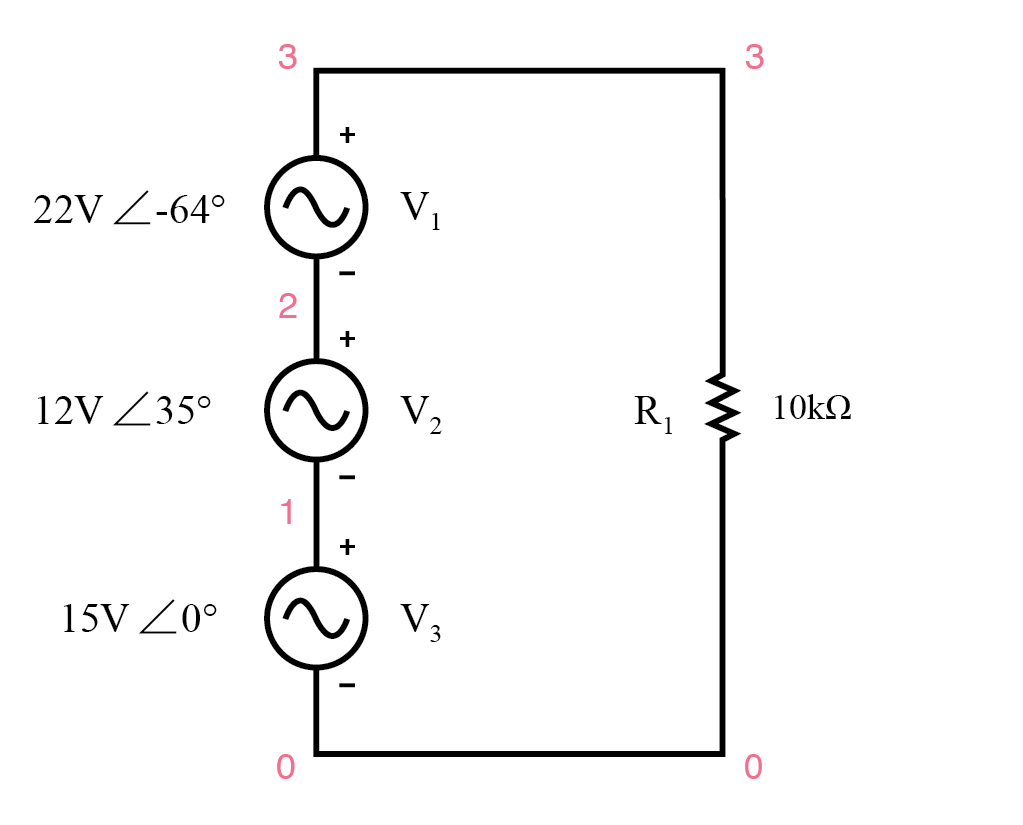
唯一の条件は、すべての変数が必要であるということです。 位相と大きさを考慮して複雑な形で表現され、すべての電圧と電流は同じ周波数でなければなりません（それらの位相関係が一定に保たれるため）。 （下の図）

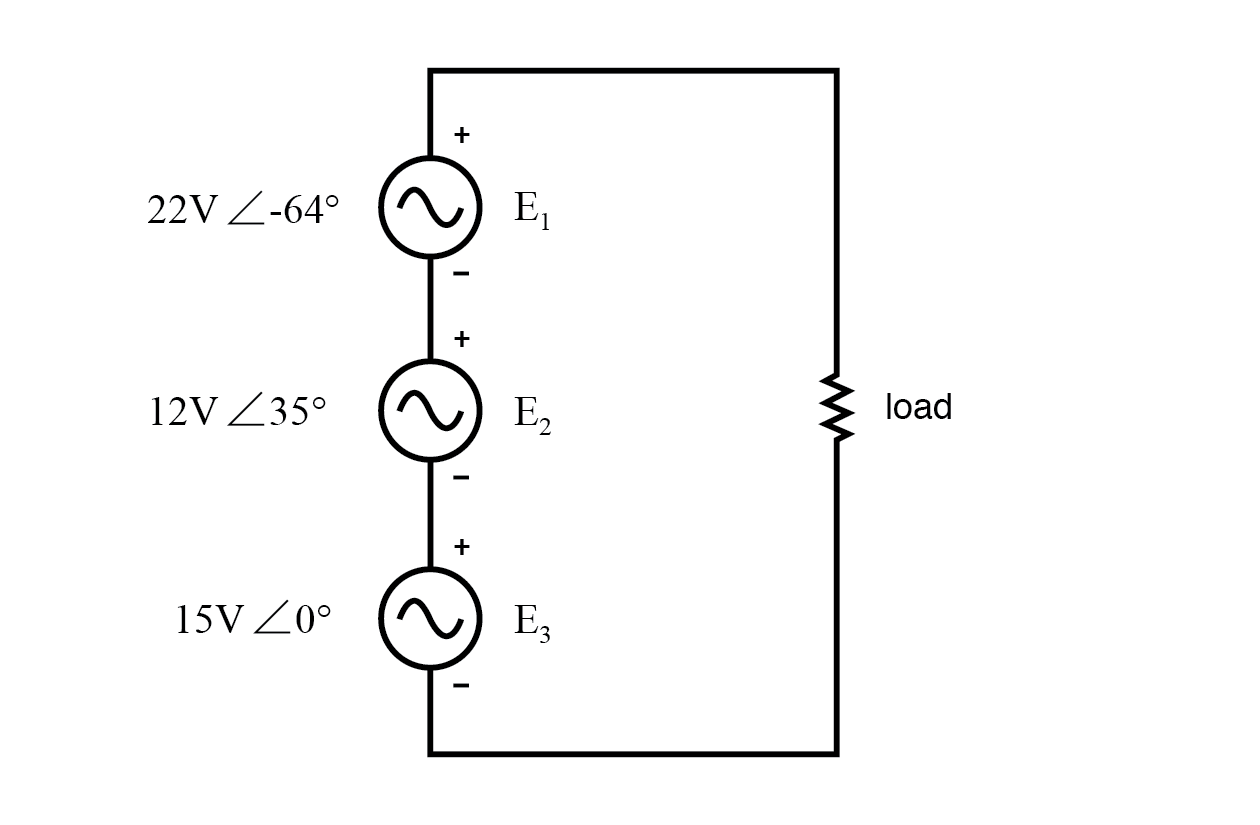
KVLを使用すると、複雑な電圧を追加できます。

3つの電圧源すべての極性マークは、負荷抵抗の両端の合計電圧を作成するために、指定された電圧が加算されるように配置されています。

AC電圧源ごとに大きさと位相角が示されていますが、周波数値は指定されていないことに注意してください。この場合、すべての周波数が等しいと見なされ、AC回路にDC規則を適用するための資格を満たします（すべての数値は複雑な形式で示され、すべて同じ周波数です）。

総電圧を求める式の設定は、次のようになります。

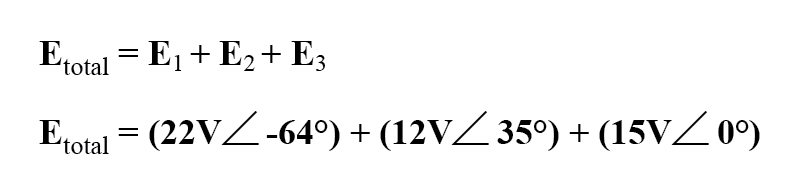
グラフィカルに、ベクトルは下の図に示すように合計されます。

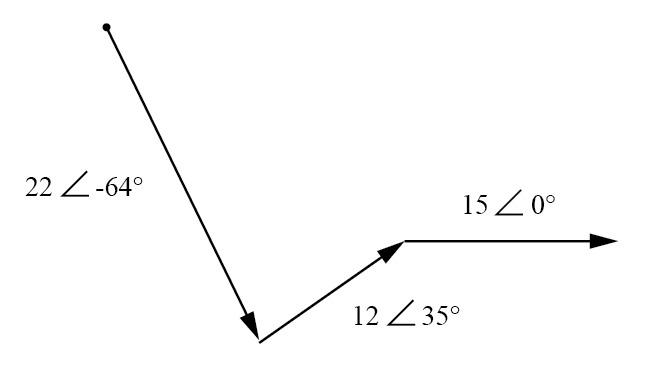
ベクトル電圧のグラフィック加算。

これらのベクトルの合計は、22ボルトのベクトルの開始点（図の左上のドット）で開始し、15ボルトのベクトルの終了点（中央の矢印の先端）で終了する結果のベクトルになります。 -図の右側）:(下の図）

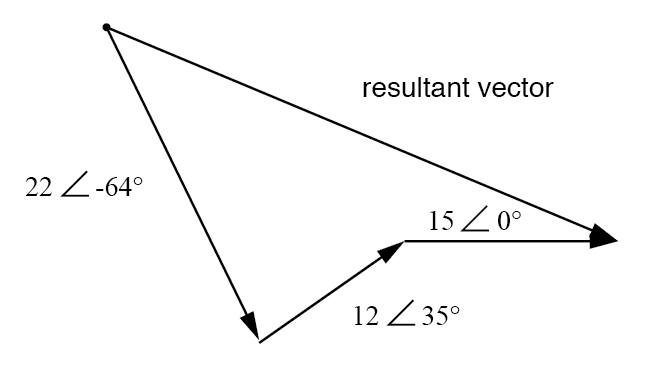
結果は、3つの元の電圧のベクトル和に相当します。

グラフィカルな画像に頼らずに、結果のベクトルの大きさと角度を決定するために、これらの極形式の複素数のそれぞれを長方形の形式に変換して追加することができます。

追加していることを忘れないでください 3つの電圧源の極性マークが相加的に方向付けられているため、これらの図は一緒になっています。

極形式では、これは36.8052ボルト∠-20.5018°に相当します。これが実際に意味することは、これら3つの電圧源で測定された電圧は36.8052ボルトであり、15ボルト（0°位相基準）より20.5018°遅れているということです。

実際の回路でこれらのポイント間に接続された電圧計は、角度ではなく、電圧の極の大きさ（36.8052ボルト）のみを示します。オシロスコープを使用して2つの電圧波形を表示し、位相シフト測定を提供できますが、電圧計は提供できません。

同じ原理がAC電流計にも当てはまります。これらは、位相角ではなく、電流の極性の大きさを示します。

これは、計算された電圧と電流の数値を実際の回路に関連付ける上で非常に重要です。

長方形の表記法は足し算と引き算に便利であり、実際にここでのサンプル問題の最終ステップでしたが、実際の測定にはあまり適用できません。

長方形の図形は極座標の図形に変換する必要があります（具体的には極座標の大きさ ）実際の回路測定に関連付ける前に。

SPICEを使用して、結果の精度を検証できます。このテスト回路では、10kΩの抵抗値はかなり任意です。 SPICEが開回路エラーを宣言して分析を中止しないようにするためにあります。

また、抵抗はAC電圧と電流のすべての周波数に対して均一に応答するため、シミュレーションの周波数（60 Hz）の選択は非常に任意です。異なる周波数に均一に応答しない他のコンポーネント（特にコンデンサとインダクタ）がありますが、それは別の問題です！ （下の図）

スパイス回路図。

 v1 1 0 ac 15 0 sin v2 2 1 ac 12 35 sin v3 3 2 ac 22 -64 sin r1 3 0 10k .ac link 1 60 60 60Hzの周波数を使用しています .print ac v（3,0）vp（3,0）をデフォルト値として 。終わり 周波数v（3）vp（3） 6.000E + 01 3.681E + 01 -2.050E + 01 

案の定、合計電圧は36.81ボルト∠-20.5°になります（「基準」波形となるように位相角が0度で任意に指定された15ボルトの電源を基準にしています）。

一見すると、これは直感に反します。 15ボルト、12ボルト、22ボルトの電源を直列に接続して、36ボルトをわずかに超える合計電圧を得るにはどうすればよいでしょうか。 DCの場合、極性に応じて電圧の数値が直接加算または減算されるため、これは不可能です。

しかし、ACを使用すると、「極性」（位相シフト）は、完全支援と完全反対の間のどこでも変化する可能性があり、これにより、このような逆説的な合計が可能になります。

同じ回路を使用して、電源の接続の1つを逆にした場合はどうなりますか？その場合、総電圧への寄与は以前とは逆になります:(下の図）

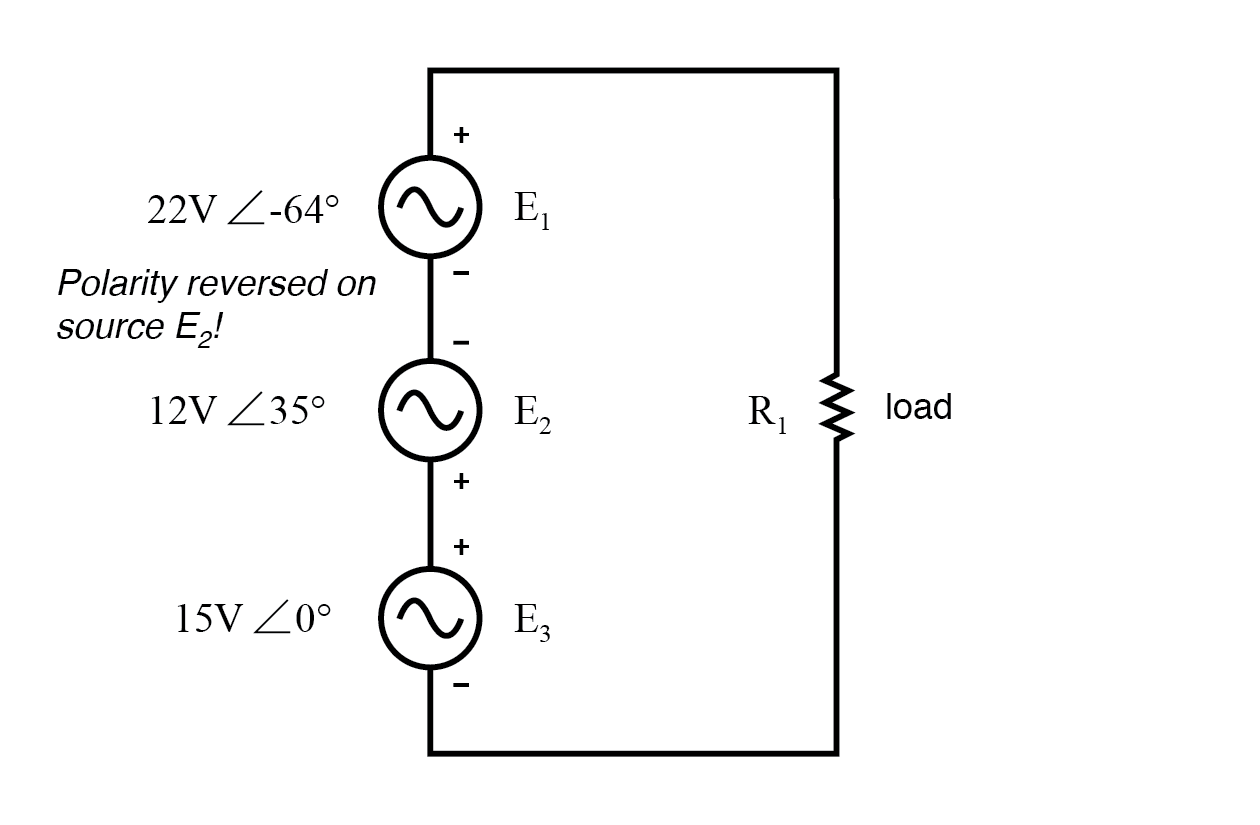
E ₂ の極性 （12V）が逆になります。

リード線が逆になっている場合でも、12ボルトの電源の位相角が35°と呼ばれていることに注意してください。電圧降下の位相角は、記載されている極性を参照して示されていることに注意してください。角度はまだ35°と書かれていますが、ベクトルは以前とは180°反対に描画されます:(下の図）

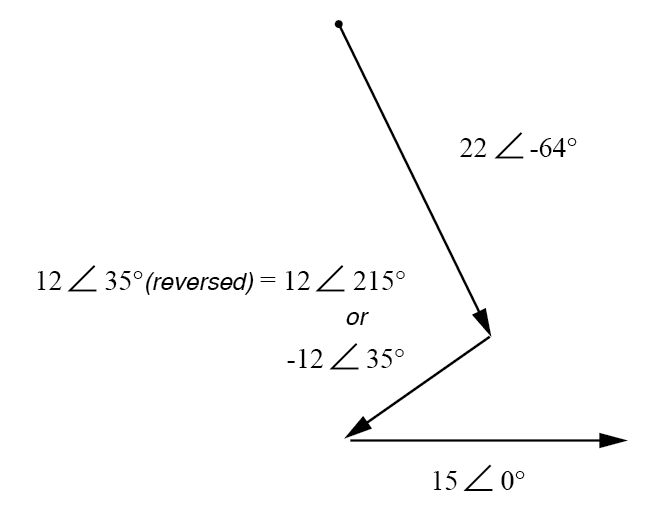
E ₂ の方向 逆になります。

結果の（合計）ベクトルは、左上の点（22ボルトのベクトルの原点）で始まり、15ボルトのベクトルの右矢印の先端で終わる必要があります:(下の図）

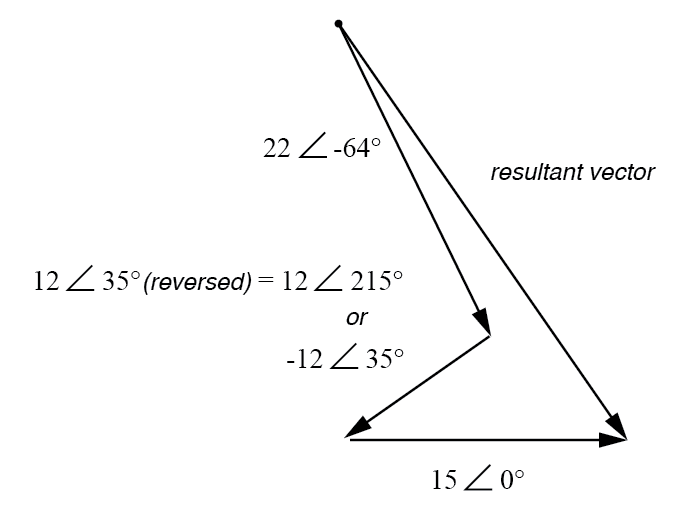
結果は、電圧源のベクトル和です。

12ボルト電源の接続反転は、極形式で2つの異なる方法で表すことができます。ベクトル角度に180°を追加する（12ボルト∠215°にする）か、大きさの符号を反転する（- 12ボルト∠35°）。いずれにせよ、長方形の形式に変換すると同じ結果が得られます：

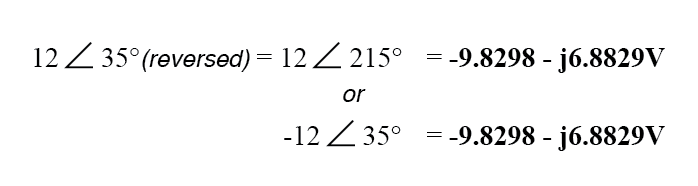
結果として生じる長方形の電圧の加算、次に：

極形式では、これは30.4964V∠-60.9368°に相当します。もう一度、SPICEを使用して計算結果を検証します。

 AC電圧の追加 v1 1 0 ac 15 0 sin v2 1 2 ac 12 35sinノード番号2と1の反転に注意してください v3 3 2 ac 22 -64 sinは、接続のスワッピングをシミュレートします r1 3 0 10k .ac lin 1 60 60 .print ac v（3,0）vp（3,0） 。終わり 周波数v（3）vp（3） 6.000E + 01 3.050E + 01 -6.094E + 01 

レビュー：

• すべての値が複雑な形式で表現および操作され、すべての電圧と電流が同じ周波数である限り、電力計算（ジュールの法則）を除いて、DC回路のすべての法則と規則がAC回路に適用されます。
• ベクトルの方向を逆にする場合（他の電圧源に対してAC電圧源の極性を逆にするのと同じ）、角度に180°を加えるか、または逆にするという2つの異なる方法のいずれかで表すことができます。大きさの兆候。
• AC回路のメーター測定値は、極の大きさに対応します。 計算値の。キルヒホッフの電圧法と電流法で要求されるように、AC回路での複素数の長方形の表現には、加算と減算を実行するのに便利ですが、直接的な経験的な同等物はありません。

関連するワークシート：

• ACネットワーク分析ワークシート
• キルヒホッフの法則ワークシート
• オームの法則ワークシート