分圧器ルール(VDR)– R、L、C回路の解決例
抵抗性、誘導性、容量性回路用の分圧「VDR」
分圧器ルールとは何ですか?
回路では、多数の要素が直列に接続されている場合、入力電圧が要素間で分割されます。また、回路では、多数の要素が並列に接続されている場合、電流は要素間で分割されます。
したがって、並列回路では電流分圧器の規則が使用され、直列回路では分圧器の規則が回路の分析と解決に使用されます。
2つ以上のインピーダンスが直列に接続されている場合、入力電圧はすべてのインピーダンスに分割されます。各要素の両端の電圧を計算するには、分圧器のルールが使用されます。分圧器の規則は、任意の要素の個々の電圧を計算するための回路解析で最も重要で単純な規則です。
分圧器ルールは、分圧器ルールとも呼ばれます。条件によっては、特定の出力電圧が必要です。しかし、ソースの特定の価値はありません。この状態で、一連のパッシブエレメントを作成し、電圧レベルを特定の値に下げます。ここでは、分圧器のルールを使用して特定の出力電圧を計算します。
回路で使用されている要素によると、分圧器の規則は3つのタイプに分類できます。抵抗分圧器、誘導分圧器、および容量性分圧器。次に、これらすべてのタイプの回路の分圧器ルールを証明します。
関連記事:
- 分圧器「VDR」計算機、例とアプリケーション
- 電圧と現在の分流の法則(VDRとCDR)の式
抵抗回路の分圧器ルール
抵抗分圧器の規則を理解するために、2つの抵抗が電圧源と直列に接続されている回路を取り上げます。
抵抗は直列に接続されているため、両方の抵抗を流れる電流は同じです。ただし、電圧は両方の抵抗で同じではありません。回路の入力電圧は両方の抵抗に分割されます。そして、個々の電圧の値は抵抗に依存します。
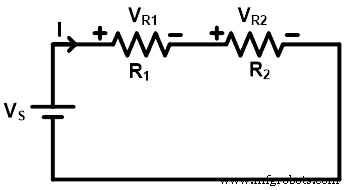
上の図に示すように、2つの抵抗R 1 およびR2 電圧源Vsと直列に接続されています 。ソースから供給される合計電流は1アンペアです。すべての要素が直列に接続されているため、単一のループが作成され、すべての要素を流れる電流は同じになります(Iアンプ)。
抵抗R 1の両端の電圧 V R1です 抵抗R2の両端の電圧 V R2です 。そして、供給された合計電圧は両方の抵抗の間で分割されます。したがって、合計電圧はV R1の合計です。 およびVR2 。
V S = V R 1 + V R 2 …(1)
オームの法則によると
V R1 = IR 1 + IR 2 …(2)
したがって、式から-(1)および(2);
V S = IR 1 + IR 2
V S = I(R 1 + R 2 )
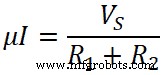
ここで、現在のIの値を方程式に入れます-(2);
V R1 = IR 1
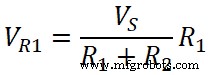
同様に;
V R2 = IR 2
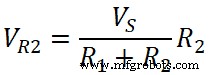
したがって、抵抗回路の分圧器の規則は、電流の分圧器の規則と反対です。ここで、抵抗器の電圧は、全電圧とその抵抗を全抵抗に掛けた比率です。
関連記事:
- テブナンの定理。解決例を含むステップバイステップガイド
- ノートンの定理。解決例を含むステップバイステップガイド
VDRを使用した抵抗回路の解決例
例-1
分圧器のルールを使用して、各抵抗器の両端の電圧を見つけます。
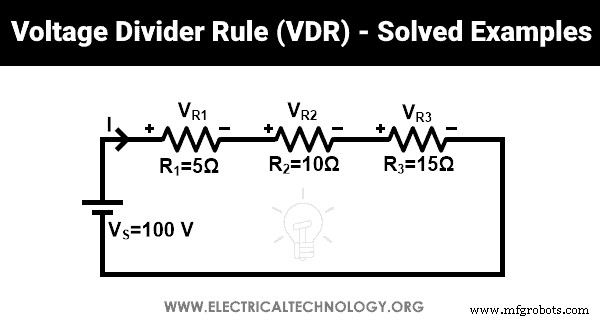
ここでは、3つの抵抗器(R 1 、R 2 、およびR 3 )は100Vの電源電圧と直列に接続されています。抵抗R1の両端の電圧 、R 2 、およびR 3 V R1です 、V R2 、およびV R3 それぞれ。
抵抗R 1の両端の電圧;
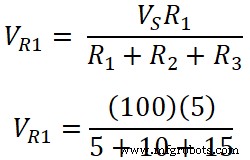
V R 3 =500/30
V R 3 =16.67 V
抵抗R2の両端の電圧;
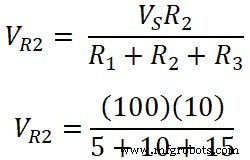
V R 3 =100/30
V R 3 =33.33 V
抵抗R 3の両端の電圧;
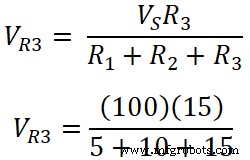
V R 3 =1500/30
V R 3 =50 V
合計電圧V T ;
V T =V R 1 + V R 2 + V R 3
V T =16.67 + 33.33 + 50
V T =100 V
V T =V S
したがって、合計電圧=は供給された電圧と同様であることが証明されます。
誘導回路の分圧器ルール
3つ以上のインダクターを持つ回路が直列に接続されている場合、インダクターを流れる電流は同じです。ただし、ソース電圧はすべてのインダクタに分割されます。この状態では、個々のインダクタの両端の電圧は、インダクタの分圧器の規則によって求めることができます。
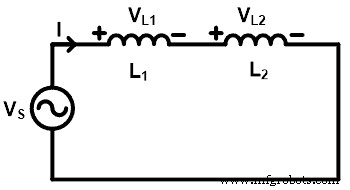
上の図に示すように、2つのインダクター(L 1 およびL2 )直列に接続されています。そして、インダクタを通過する総電流。インダクタ両端の電圧L1 V L1です インダクタ両端の電圧L2 V L2です 。そして供給電圧はVS 。ここで、電圧V L1を見つける必要があります。 およびVL2 インダクタ分圧器のルールを使用します。
インダクタの電圧の式を知っているので;
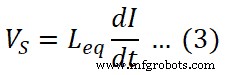
ここでL eq は回路の総インダクタンスです。ここでは、2つのインダクタが直列に接続されています。したがって、等価インダクタンスは両方のインダクタンスの合計です。
L eq = L 1 + L 2
From、方程式-(3);
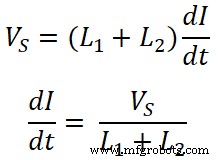
これで、インダクタL 1の両端の電圧 です;
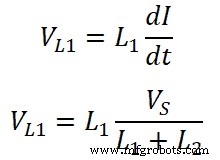
同様に、インダクタL 2の両端の電圧 です;
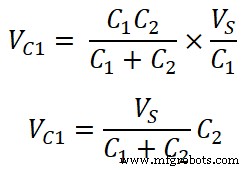
したがって、インダクタの分圧器の規則は抵抗と同じであると言えます。
VDRを使用した誘導回路の解決例
例-2
分圧器のルールを使用して、特定の回路の各インダクタの両端の電圧を見つけます。
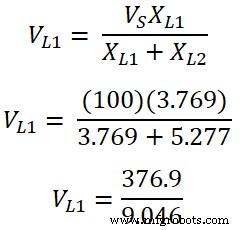
ここでは、2つのインダクタが100V、60Hzのソースと直列に接続されています。インダクタ両端の電圧L1 V L1です インダクタ両端の電圧L2 V L2です 。
インダクタ間の電圧を見つけるには、各インダクタの無効インピーダンスを見つける必要があります。
インダクタL 1の両端の無効インピーダンス です;
X L 1 =2πf L 1
X L 1 =2×3.1415×60x10×10 -3
X L 1 =3.769Ω
インダクタL2の両端の無効インピーダンス です;
X L 2 =2πf L 2
X L 2 =2×3.1415×60x14×10 -3
X L 2 =5.277Ω
分圧器の規則に従って、
インダクタL 1の両端の電圧 です;
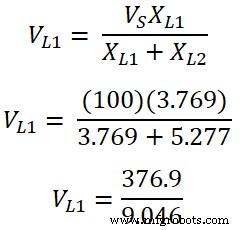
V L 1 =41.66 V
インダクタL2の両端の電圧 です;
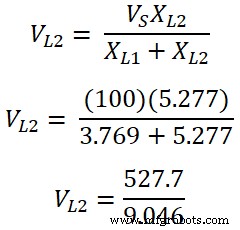
V L 2 =58.35 V
合計電圧V T です;
V T =V L 1 + V L2
V T =41.66 + 58.35
V T =100 V
V T =V S
したがって、合計電圧は供給電圧と同じです。
分圧器のルール 容量性 回路
コンデンサでは、分圧器の規則はインダクタと抵抗とは異なります。コンデンサの分圧器の法則を計算するために、2つ以上のコンデンサが直列に接続されている回路を考えてみましょう。
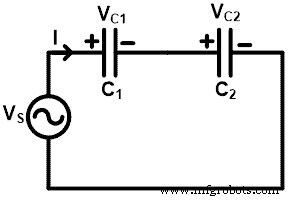
ここでは、2つのコンデンサが電源電圧V Sと直列に接続されています。 。ソース電圧は2つの電圧に分割されます。 1つの電圧はコンデンサC1の両端にあります 2番目の電圧はコンデンサC2の両端にあります 。
コンデンサCの両端の電圧 1 V C1です コンデンサC2の両端の電圧 V C2です 。上の回路図に示すように、両方のコンデンサが直列に接続されています。したがって、等価容量は次のようになります。
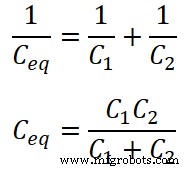
ソースから提供される合計料金はQです;
Q = C eq V S
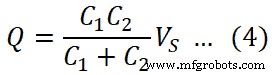
コンデンサCの両端の電圧 1 です;
V C1 = Q 1 / C 1
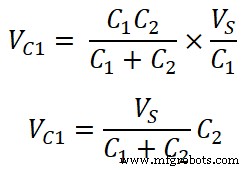
コンデンサCの両端の電圧 2 です;
V C2 = Q 1 / C 2
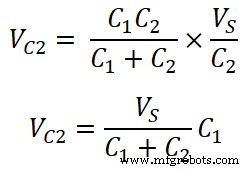
したがって、計算から、コンデンサの両端の個々の電圧は、合計ソース電圧と反対の容量の合計容量に対する乗算の比率であると言えます。
VDRを使用した容量性回路の解決例
例-3
分圧器のルールを使用して、特定のネットワークの各コンデンサの両端の電圧を見つけます。
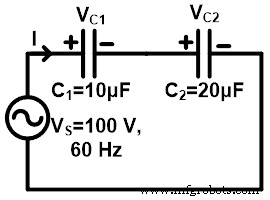
ここでは、2つのコンデンサが100 V、60Hzのソースと直列に接続されています。コンデンサC1の両端の電圧 V C1です コンデンサC2の両端の電圧 V C2です 。
各コンデンサの両端の電圧を計算するには、容量性インピーダンスを見つける必要があります。
C1の両端の容量性インピーダンス です;
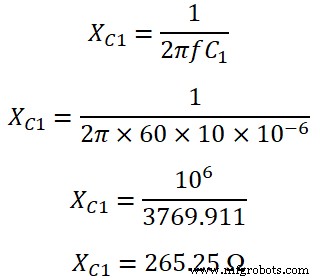
C2の両端の容量性インピーダンス です;
X C 2 =1 /(2π f C 2 )
X C 2 =1 /(2π×60×20×10 -6 )
X C 2 =10 -6 / 7539.822
X C 2 =132.63Ω
分圧器の規則に従って、コンデンサC 1の両端の電圧 です;
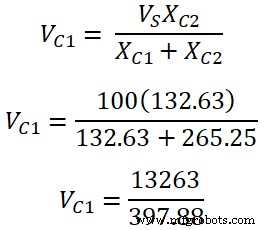
V C1 =33.33 V
コンデンサCの両端の電圧 2 です;
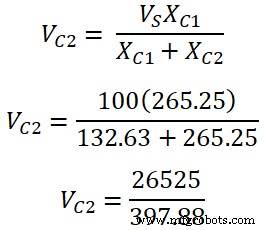
V C 2 =66.67 V
コンデンサ両端の合計電圧V T です;
V T =V C 1 + V C2
V T =33.33 + 66.67
V T =100 V
V T =V S
関連する電気回路解析チュートリアル:
- SUPERNODE回路解析–解決例を使用したステップバイステップ
- SUPERMESH回路解析–解決例を使用したステップバイステップ
- 分圧器ルール「VDR」計算機–例とアプリケーション
- 現在の分流の法則「CDR」計算機–例とアプリケーション
- キルヒホッフの電流および電圧法(KCLおよびKVL)|解決した例
- クラメルの公式計算機–電気回路用の2および3方程式システム
- 電気電子工学計算機
- 5000以上の電気電子工学の公式と方程式
産業技術



