ミルマンの定理– ACおよびDC回路の分析–例

ACおよびDC回路のミルマンの定理–ステップバイステップで解決された例

ミルマンの定理

ミルマンの定理は、並列の分岐のみがある場合に回路解析で使用されます。したがって、この定理は、回路の端の電圧を計算するのに役立ちます。ミルマンの定理は、並列ネットワークを含む回路にのみ適用できます。

ミルマンの定理は、テブナンの定理を組み合わせたものです。 およびノートンの定理 。この定理は、並列ジェネレータ定理とも呼ばれます。 。この定理は、電気工学の教授 Jacob Millmanによって提案されました。 。そして彼の名前にちなんで、この定理はミルマンの定理と呼ばれています。

ミルマンの定理は次のように述べています;

つまり、特定のネットワークの並列ブランチ間の電圧を見つけることができます。この定理は、下の図に示すように、多数のソースが接続されている場合にネットワークの複雑さを軽減します。

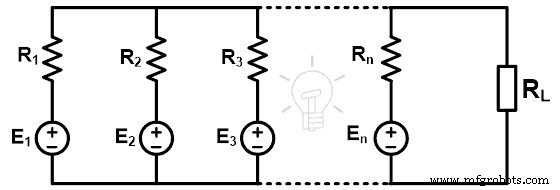
ミルマンの定理によると;負荷両端の電圧は;

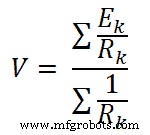
• 関連記事：テブナンの定理。解決例を含むステップバイステップガイド

数式

上の図に示すように、n個の電圧源（E ₁ ）を持つ回路 、E ₂ 、E ₃ 、…、E _n ）。そして、ソースの内部抵抗はR ₁です。 、R ₂ 、R ₃ 、…、R _n それぞれ。ミルマンの定理によれば、どの回路も以下のネットワークに置き換えることができます。次の図は、ミルマンの等価回路を示しています。

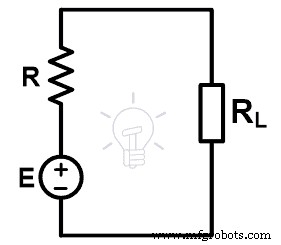
次に、電圧源（E）と等価抵抗（R）の値を見つける必要があります。上記の回路は、テブナンの等価回路に似ています。したがって、電圧源（E）はテブナンの等価電圧（V _TH ）と同じであると言えます。 ）および等価抵抗はテブナンの等価抵抗（R _TH 。

簡単に計算できるノートンの等価回路が見つかりました。そのために、ソース変換を行います。そして、すべての電圧源を電流源に変換します。

電圧源と直列に接続された内部抵抗があります。ソース変換後、電圧ソースが電流ソースに変換され、内部抵抗が電流ソースと並列に接続されます。したがって、上記の回路は下の図に示すように変換されます。

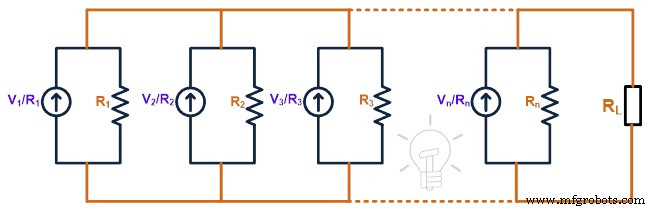
オームの法則によれば、電流源の値はE ₁ / R ₁ 、E ₂ / R ₂ 、E ₃ / R ₃ 、…、E _n / R _n 。ここで、ノートンの等価電流（I _N ）、負荷端子を短絡する必要があります。そして、電流がそのブランチを通過するのを見つけます。

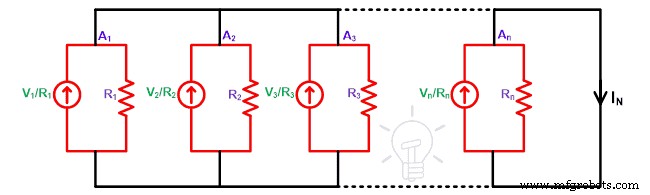
ノードA ₁で 、電流は2つのパスに分割されます。 1つのパスは、抵抗R ₁を経由します。 2番目のパスは短絡したブランチからのものです。ご存知のように、電流は常に低抵抗経路を流れます。したがって、この状態では、電流全体が短絡した分岐を通過します。そして、抵抗を流れる電流はゼロです。

これと同じことがノードA ₂のすべてのソースで発生します 、A ₃ 、…、A _n 。そして、すべての抵抗器を流れる電流はゼロです。

ここで、ノードA ₂ 、ノードA ₁からの電流 が追加されます。同様に、ノードA3では、ノードA ₂からの電流 が追加されます。したがって、ノードA _nで 、すべてのノードからの電流が追加されました。総電流はすべての電流の合計であり、ノートンの電流（I _N ）として知られています。 。

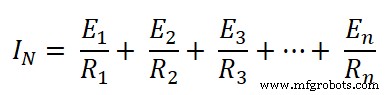
つまり、ノートンの同等の電流が見つかりました。ここで、ノートンの等価抵抗を見つける必要があります。そのためには、電流源を開回路にし、電圧源を短絡することによって、回路に存在するすべてのエネルギー源を取り除く必要があります。

上の図では、現在のソースのみがあります。開回路によってこれらの電流源を取り除きます。そして、等価抵抗を計算するために負荷を取り除く必要があります。したがって、残りの回路は次の図のようになります。

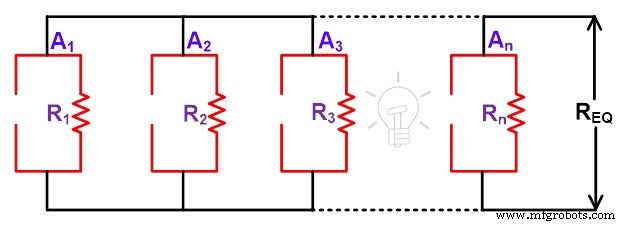
上の図に示すように、すべての抵抗が並列に接続されていることがわかります。そして、この並列の組み合わせは等価抵抗に等しくなります。

R _eq = R _N =R ₁ || R ₂ || R ₃ …|| R _n

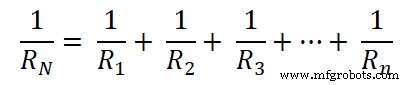
次に、下の図に示すように、これらの値をノートンの等価回路に入れます。

このノートンの等価回路をテブナンの等価回路に変換すると、ノートン電流I _NからEとRの値を計算できます。 およびノー​​トン抵抗R_N 。

オームの法則によると;

E =I _N x R _N

上記の方程式をn個の分岐に対して一般的な形式で作成しましょう。

つまり、電圧源の値があります。また、等価抵抗の値はノートンの等価抵抗に等しくなります。したがって、ミルマンの等価回路を得ることができます（図-2）。

• 関連記事：ノートンの定理。解決例を含むステップバイステップガイド

ミルマンの定理に従うための手順

ステップ-1 ミリマンの定理は、より多くの並列分岐を持つネットワークまたは回線にのみ適用できます。したがって、内部抵抗と直列に接続された電圧源を含む多数の並列分岐がある回路を解く必要があると想定します。

ステップ2 内部抵抗または直列に接続された抵抗と電圧源のリストを作成します。

ステップ3 電圧源を短絡した場合の負荷端子間の等価抵抗（R）を求めます。

ステップ4 ミルマンの定理を適用し、負荷端子間の電圧（E）の値を見つけます。そのためには式-1を使用します。この電圧は負荷両端の電圧です。

ステップ5 RとEの値をミルマンの等価回路に入れます（図-2）。

ステップ-6 ループにKVLを適用して、電流が負荷を通過することを確認します。

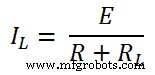
• 関連記事：重ね合わせの原理–解決された例を使用した回路解析

ミルマンの定理を使用したDC回路の分析

例1

ミルマンの定理を使用して、負荷端子の両端の電流と電圧を見つけます。

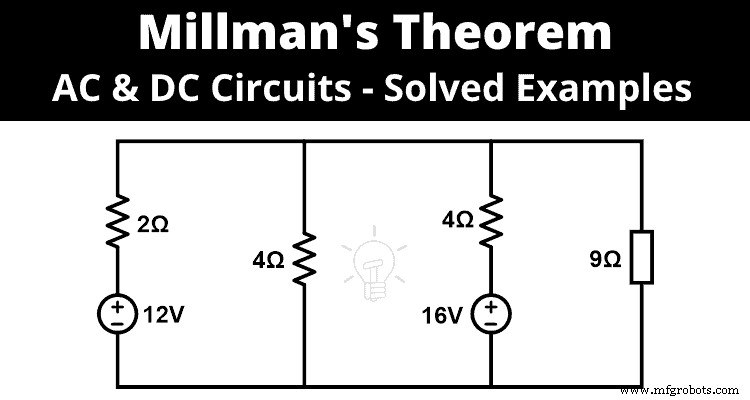
ステップ-1 上の図を見ると、4つのブランチすべてが並列に接続されていると言えます。そして、ミルマンの定理を適用することができます。

ステップ2 ロードブランチを除いて3つのブランチがあります。したがって、以下に示すように、3つの電圧と3つの抵抗があります。

E ₁ =12VおよびR ₁ =2Ω

E ₂ =0VおよびR ₁ =4Ω

E ₃ =16VおよびR ₁ =4Ω

ステップ3 等価抵抗を求めるには、電圧源を短絡して取り外し、負荷端子を開く必要があります。したがって、残りの図は下の図に示されています。

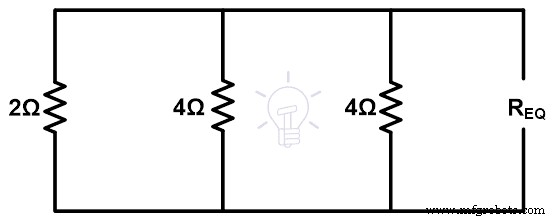
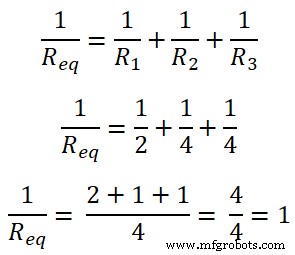
R _eq =1Ω

上の図に示すように、すべての抵抗は並列です。したがって、等価抵抗は次のようになります。

ステップ4 次に、ミルマンの定理を適用します。

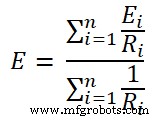
この例では、3つのブランチがあります。したがって、n=3を使用します。

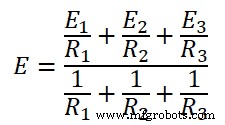
上記の値をこの式に入れます。

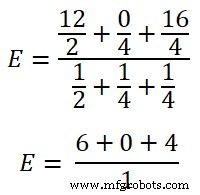
E =10V

これは負荷端子の両端の電圧です。

ステップ5 これらの値をミルマンの等価回路に入れてください。

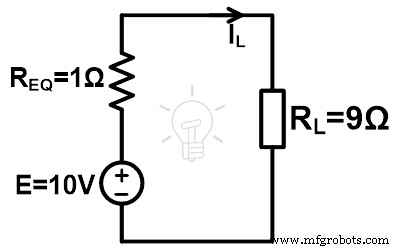
ステップ-6 オームの法則によると、

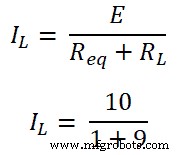
I _L =1A

したがって、負荷の両端の電圧は10 Vで、負荷を流れる電流は1Aです。

• 関連記事：テレゲンの定理–解決された例とMATLABシミュレーション

ミルマンの定理を使用したAC回路の分析

例2

ミルマンの定理を使用して、負荷端子間の電流と電圧を見つけます。

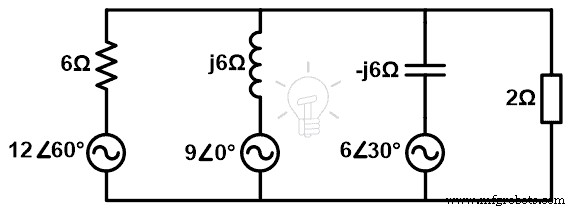
ステップ-1 上の図に示すように、4つのブランチが並列に接続されています。したがって、ミルマンの定理を適用できます。

ステップ2 ロードブランチを考慮しない場合、3つのブランチがあります。計算を簡単にするために、電圧とインピーダンスをリストします。 AC回路の場合、抵抗の代わりにワードインピーダンスを使用する必要があります。

電圧源の値は極形式で示されます。ただし、インピーダンスの値は長方形で示されています。したがって、電圧源の値を極形式に変換する必要があります。

V ₁ =12∠60°=6+ j 10.392

V ₂ =9∠0°=9+ j 0

V ₃ =6∠30°=5.196+ j 3

インピーダンスは長方形の形式で示されます。そのため、そのままリストします。

Z ₁ =6Ω

Z ₂ = j 6Ω

Z ₃ =– j 6Ω

ステップ3 等価インピーダンスを見つけます。上記の例に示すように、短絡によってすべての電圧源を除去する必要があります。そして残りの回路は下図のようになります。

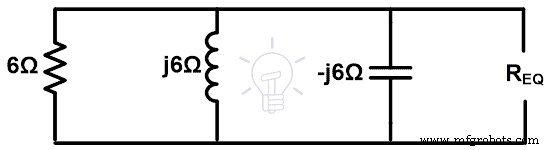
ここでは、すべてのインピーダンスが並列に接続されています。したがって、等価インピーダンスは次のようになります。

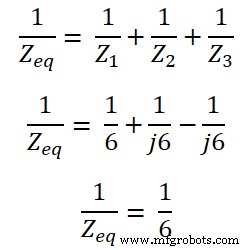
Z _eq =6Ω

ステップ4 次に、ミリマンの定理を適用します。

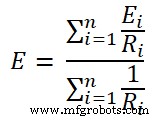
ここには、3つのブランチがあります。したがって、nは3に等しくなります。

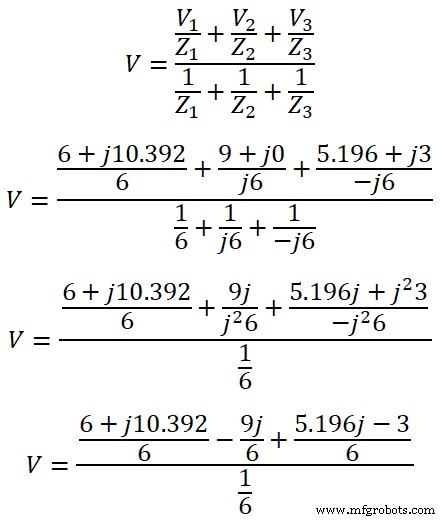
V =6 + 1 j 0.392 – j 9 + j 5.196 – 3

V =3 + j 6.588

次に、RMS値を見つける必要があります。

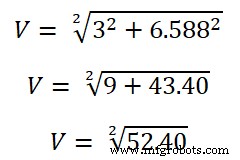
V =7.23V

ステップ5 これらの値をミルマンの等価回路に入れてください。

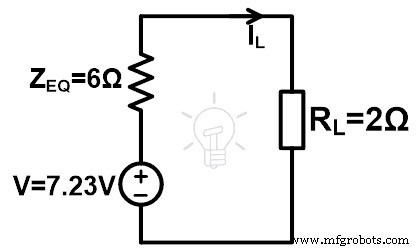
ステップ-6 オームの法則によると、

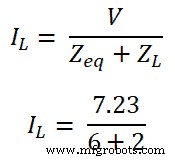
I _L =0.9A

• 関連記事： ACおよびDC回路の最大電力伝達定理
  

ミルマンの定理の制限

ミルマンの定理は、ネットワークを解決するのに非常に役立ちます。ただし、以下のような制限があります。

• この定理は、独立したソース間に依存したソースがある回路には適用されません。
• 独立したソースが2つ未満の回路の場合、この定理は役に立ちません。
• この定理は、直列要素のみを持つ回路には適用されません。
• ソース間に要素が接続されている場合、この定理は適用できません。

ミルマンの定理の適用

ミルマンの定理は、複雑な回路を解くためのネットワーク解析で広く使用されています。ミルマンの定理の適用は以下のとおりです。

• ミルマンの定理は、多数の電圧源で利用できる並列分岐の数が多い場合に、負荷インピーダンスの電圧と電流を見つけるのに最も役立ちます。
• この定理の計算は簡単です。これ以上方程式を使用する必要はありません。
• この定理は、オペアンプのような複雑な要素を持つ複雑な回路を解くために使用されます。

関連する電気回路解析チュートリアル：

• SUPERNODE回路解析–解決例を使用したステップバイステップ
• SUPERMESH回路解析–解決例を使用したステップバイステップ
• キルヒホッフの電流および電圧法（KCLおよびKVL）|解決した例
• クラメルの公式計算機–電気回路用の2および3方程式システム
ホイートストンブリッジ–回路、動作、派生、およびアプリケーション
• 電気電子工学計算機
• 5000以上の電気電子工学の公式と方程式