相互インダクタンスと基本動作

導電性コアに巻き付けられたインダクタの動作

強磁性体のループの周りに絶縁ワイヤのコイルを巻き付け、このコイルにAC電圧源で通電するとします:(下の図（a））

強磁性ループの絶縁巻線には誘導性リアクタンスがあり、AC電流を制限します

インダクターとして、この鉄心コイルは、誘導性リアクタンスで印加電圧に対抗し、次の式で予測されるようにコイルを流れる電流を制限すると予想されます。

X _L =2πfLおよびI =E / X（またはI =E / Z）

ただし、この例では、デバイス内の電圧、電流、磁束の相互作用をより詳細に調べる必要があります。

キルヒホッフの電圧法則は、ループ内のすべての電圧の代数和がゼロに等しくなければならない方法を説明しています。この例では、この電気の基本法則を適用して、電源と誘導コイルのそれぞれの電圧を記述することができます。

ここでは、他の1ソース、1負荷回路と同様に、負荷の両端で降下する電圧は、接続ワイヤの抵抗とともに降下する電圧がゼロであると仮定して、ソースから供給される電圧と等しくなければなりません。

言い換えると、負荷（誘導コイル）は、ソース電圧とバランスを取り、代数ループ電圧の合計がゼロになるように、ソースと同じ大きさの反対の電圧を生成する必要があります。

この反対の電圧はどこから発生しますか？負荷が抵抗器である場合（上の図（b））、電圧降下は電気エネルギー損失、つまり抵抗器を流れる電荷キャリアの「摩擦」に起因します。

完全なインダクター（コイルワイヤーに抵抗がない）を使用すると、反対の電圧は別のメカニズムから発生します：反応 鉄心の磁束の変化に。 AC電流が変化すると、磁束Φが変化します。フラックスを変更すると、カウンターEMFが発生します。

電圧、電流、磁束の関係

Michael Faradayは、次の方程式を使用して、磁束（Φ）と誘導電圧の数学的関係を発見しました。

ワイヤーコイルの両端の瞬間的な電圧（任意の瞬間に降下する電圧）は、コアの周りのそのコイルの巻き数（N）に磁束の瞬間的な変化率（dΦ/ dt）を掛けたものに等しくなります。コイル付き。

グラフ（下の図）では、これは正弦波のセットとして表示され（正弦波の電圧源を想定）、磁束波は電圧波より90°遅れています：

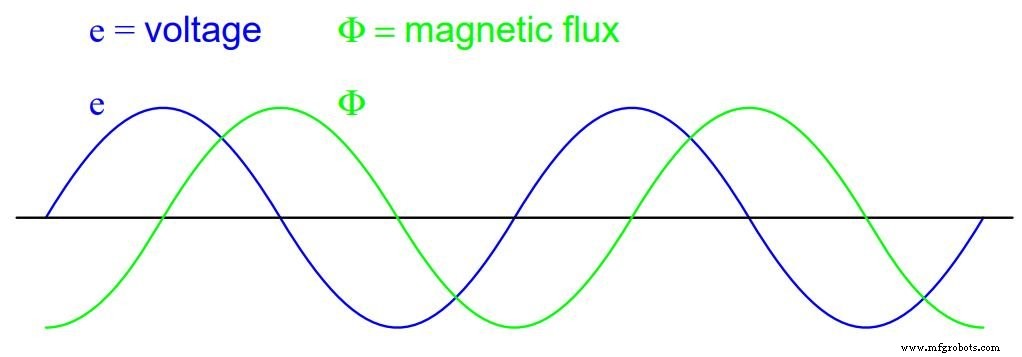
電流のような磁束は、印加電圧より90°遅れます

これが、インダクタを流れる交流が印加電圧波形を90°遅らせる理由です。これは、変化率が印加電圧と同相の逆電圧を生成する変化する磁束を生成するために必要なものだからです。

>

コアに起磁力（mmf）を提供する機能があるため、この電流は磁化電流と呼ばれることもあります。 。

鉄のB / H磁化曲線が非線形であるため、鉄心インダクタを流れる電流は完全に正弦波（正弦波形状）ではないことに注意してください。

実際、インダクタを安価に構築し、鉄をできるだけ少なくすると、磁束密度が高レベルに達し（飽和に近づく）、次の図のような磁化電流波形が生じる可能性があります。

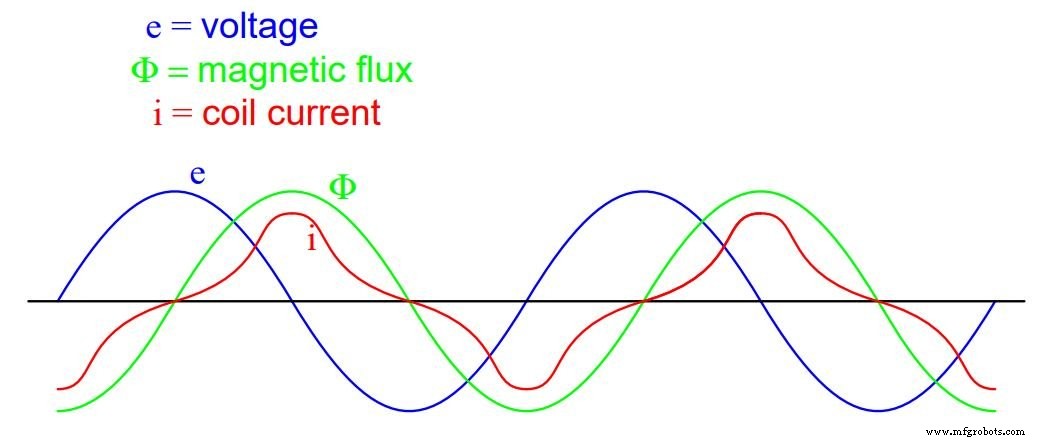
磁束密度が飽和に近づくと、磁化電流波形が歪むようになります

強磁性体が磁束飽和に近づくと、磁束（Φ）を均等に増加させるために、不釣り合いに大きなレベルの起磁力（mmf）が必要になります。

mmfは起磁力コイルを流れる電流に比例するため（mmf =NI、ここで「N」はコイル内のワイヤの巻き数、「I」はコイルを流れる電流）、必要なものを供給するために必要なmmfの大幅な増加磁束が増加すると、コイル電流が大幅に増加します。

したがって、コイル電流は、歪まない磁束波形を維持するためにピークで劇的に増加し、上記のプロットの電流波形のベル型の半サイクルを説明します。

エキサイティングな電流とその影響

鉄心内のエネルギー損失により、状況はさらに複雑になります。ヒステリシス電流と渦電流の影響により、電流波形がさらに歪んで複雑になり、正弦波がさらに小さくなり、印加電圧波形から90°未満遅れるように位相が変化します。

コア内のすべての磁気効果（dΦ/ dt磁化とヒステリシス損失、渦電流損失など）の合計から生じるこのコイル電流は、励起電流と呼ばれます。 。

鉄心インダクタの励起電流の歪みは、非常に低い磁束密度用に設計および動作されている場合、最小限に抑えることができます。一般的に、これには大きな断面積のコアが必要であり、インダクタがかさばり、高価になる傾向があります。

ただし、簡単にするために、この例のコアは飽和状態にはほど遠いものであり、すべての損失がないため、完全に正弦波の励起電流が発生すると仮定します。

インダクタの章ですでに見たように、電流波形が電圧波形と90°位相がずれていると、電力がインダクタによって交互に吸収されて回路に戻される状態が発生します。

インダクタが完全である場合（ワイヤ抵抗、磁気コア損失などがない場合）、ゼロ電力を消費します。

ここで、同じインダクターデバイスを考えてみましょう。ただし、今回は同じ鉄心に2番目のコイル（下の図）を巻き付けています。最初のコイルには primary というラベルが付けられます コイル、2番目はセカンダリとラベル付けされます ：

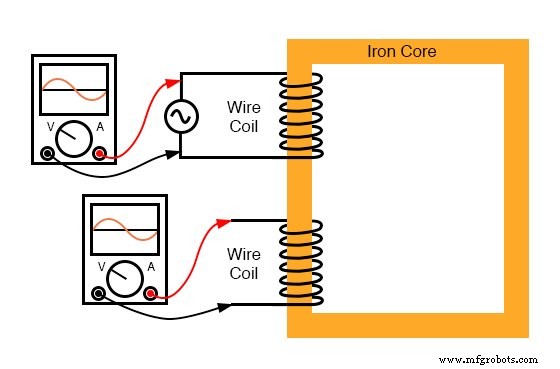
一次コイル（AC駆動）と二次コイルを備えた強磁性コア。

相互誘導

この二次コイルが一次コイルと同じ磁束変化を経験し（共通のコアを通る磁束が完全に封じ込められていると仮定すると）、コアの周りの巻数が同じである場合、電圧は印加電圧はその長さに沿って誘導されます。

次のグラフ（下の図）では、誘導電圧波形は、単に一方を他方から区別するために、ソース電圧波形よりもわずかに小さく描かれています。

開回路の二次側は、一次側と同じ磁束Φを見ます。したがって、誘導された二次電圧e _s 一次電圧e _p と同じ大きさと位相です 。

この効果は相互インダクタンスと呼ばれます ：もう一方のコイルの電流の変化に応じて、一方のコイルに電圧が誘導されます。通常の（自己）インダクタンスと同様に、ヘンリーの単位で測定されますが、通常のインダクタンスとは異なり、文字「L」ではなく大文字の「M」で表されます。

二次コイルは開回路であるため、電流は流れません。ただし、負荷抵抗を接続すると、誘導電圧と同相の交流電流がコイルを流れます（抵抗の両端の電圧と抵抗を流れる電流は常に 互いに同相）。 （下の図）

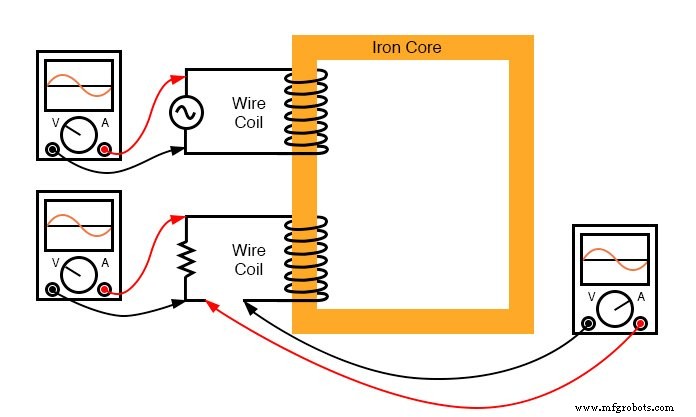
二次側の抵抗負荷には、電圧と電流が同相です。

最初は、この二次コイル電流がコアに追加の磁束を引き起こすと予想されるかもしれません。実際、そうではありません。より多くの磁束がコアに誘導されると、より多くの電圧が一次コイルに誘導される電圧になります（e =dΦ/ dtであることを忘れないでください）。

キルヒホッフの電圧法則に従って、印加電圧とバランスを取るために、一次コイルの誘導電圧は同じ大きさと位相のままでなければならないため、これは起こり得ません。したがって、コア内の磁束は二次コイル電流の影響を受けません。

ただし、何をするか 変化は、磁気回路の起磁力の量です。

起磁力

起磁力は、電流がワイヤを流れるときに発生します。通常、このmmfには、mmf =ΦRの「起磁力の法則」の式に従って、磁束が伴います。

ただし、この場合、追加の磁束は許可されないため、二次コイルのmmfが存在する唯一の方法は、同じ大きさで逆位相の反作用するmmfが一次コイルによって生成される場合です。

実際、これが起こり、一次コイルに交流電流が形成され、二次コイルの電流と180°位相がずれて、この反作用起磁力が生成され、追加のコア磁束が防止されます。

位相関係を明確にするために、極性マークと現在の方向矢印が図に追加されています:(下の図）

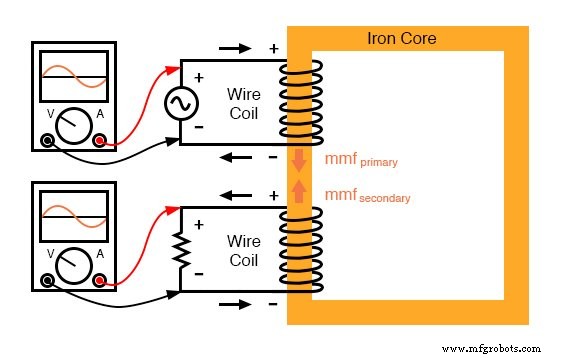
荷重を加えても、流束は一定に保たれます。ただし、反作用する起磁力は、ロードされたセカンダリによって生成されます。

このプロセスが少しわかりにくい場合でも、心配する必要はありません。変圧器のダイナミクスは複雑な問題です。理解しておくべき重要なことは、これです。AC電圧が一次コイルに印加されると、コアに磁束が発生し、ソース電圧と同相の二次コイルにAC電圧が誘導されます。

負荷に電力を供給するために二次コイルを介して引き出される電流は、一次コイルに対応する電流を誘導し、ソースから電流を引き込みます。

相互インダクタンスとトランス

一次コイルがAC電圧源に対して負荷のように動作していること、および二次コイルが抵抗器に対してソースとしてどのように動作しているかに注意してください。

エネルギーが単に一次コイル回路に交互に吸収されて戻されるのではなく、エネルギーは現在結合されています 二次コイルに送られ、そこで散逸（エネルギー消費）負荷に供給されます。ソースが「知っている」限り、抵抗に直接電力を供給します。

もちろん、印加電圧より90°遅れる追加の一次コイル電流もあります。これは、コアを磁化して、ソースとのバランスを取るために必要な電圧（励起電流）を生成するのに十分です。 。

このタイプのデバイスをトランスフォーマーと呼びます 、それは電気エネルギーを磁気エネルギーに変換し、次に再び電気エネルギーに戻すからです。その動作は、2つの固定コイル間の電磁誘導と、大きさと「極性」が変化する磁束に依存するため、変圧器は必然的にACデバイスです。

その回路図記号は、同じ磁気コアを共有する2つのインダクター（コイル）のように見えます:(下の図）

変圧器の回路図記号は、強磁性コアを示す線で区切られた2つのインダクター記号で構成されています。

上記の記号では、2つのインダクタコイルを簡単に区別できます。垂直線のペアは、両方のインダクタに共通の鉄心を表しています。多くの変圧器には強磁性のコア材料がありますが、そうでないものもあり、それらの構成インダクタは空気を介して磁気的に結合されています。

次の写真は、ガス放電照明に使用されるタイプの電源トランスを示しています。ここでは、2つのインダクタコイルが鉄心に巻かれているのがはっきりとわかります。ほとんどの変圧器の設計は、保護のためにコイルとコアを金属フレームで囲んでいますが、この特定の変圧器は表示用に開いているため、その説明の目的を十分に果たします（下の図）：

ガス放電照明変圧器の例。

一次および二次巻線

ワイヤーの両方のコイルは、銅色のワニス絶縁でここに見ることができます。上のコイルは下のコイルよりも大きく、コアの周りの「ターン」の数が多くなっています。変圧器では、インダクタコイルは巻線と呼ばれることがよくあります。 、ワイヤーが巻かれる製造プロセスに関連して コア材料の周り。

最初の例でモデル化されているように、変圧器の給電インダクタはプライマリと呼ばれます。 巻線、電力が供給されていないコイルはセカンダリと呼ばれます 巻線。

次の写真（下の図）では、変圧器が半分にカットされており、鉄心と両方の巻線の断面が露出しています。前に示したトランスと同様に、このユニットも巻数の異なる一次巻線と二次巻線を利用しています。

ワイヤゲージは、一次巻線と二次巻線で異なることもわかります。ワイヤゲージのこの不一致の理由は、この章の次のセクションで明らかになります。

さらに、この写真の鉄心は、中実の部分ではなく、多くの薄いシート（積層）でできていることがわかります。この理由については、この章の後のセクションでも説明します。

変圧器の断面図はコアと巻線を示しています。

SPICEを使用した単純なトランスフォーマーアクション

SPICEを使用して、シミュレートされたトランスの1次巻線と2次巻線を一対の「相互」インダクタとして設定することで、単純なトランスの動作を簡単に示すことができます（下図）。

磁場結合の係数は、SPICE回路の説明の「k」線の終わりに示されています。この例は、ほぼ完全（1.000）に設定されています。この係数は、2つのインダクタがどれだけ密接に「リンク」されているかを示します。これらの2つのインダクタが磁気的に結合されているほど、それらの間のエネルギー伝達はより効率的になるはずです。

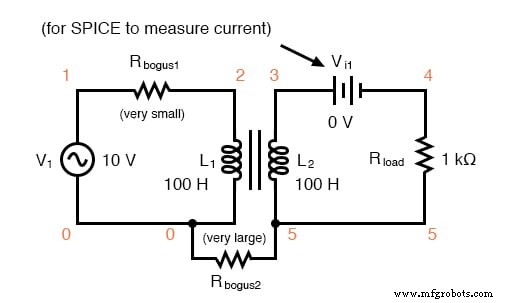
結合インダクタ用のスパイス回路。

トランスフォーマー v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0100 l2 3 5100 **この行は、2つのインダクターがSPICEにあることを示しています ** l1とl2は磁気的に「リンク」されています k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac lin 1 60 60 .print ac v（2,0）i（v1） .print ac v（3,5）i（vi1） 。終わり 

注：R _偽物 SPICEの特定の癖を満たすには、抵抗が必要です。 1つ目は、電圧源とL ₁ の間の連続ループを切断します。 これはSPICEでは許可されません。 2つ目は、SPICEが接地されていない回路では機能できないため、2次回路から接地（ノード0）へのパスを提供します。

 freq v（2）i（v1） 6.000E + 01 1.000E + 019.975E-03一次巻線 周波数v（3,5）i（vi1） 6.000E + 01 9.962E + 009.962E-03二次巻線 

両方の巻線のインダクタンスが等しい場合（それぞれ100ヘンリー）、AC電圧と電流は2つでほぼ等しいことに注意してください。一次電流と二次電流の違いは、先に述べた磁化電流です。コアを磁化するために必要な90°の遅れ電流です。

ここに見られるように、それは通常、負荷によって誘導される一次電流と比較して非常に小さいので、一次電流と二次電流はほぼ等しくなります。ここに表示されているのは、変圧器の効率の非常に典型的なものです。

最新の電源トランスの設計では、95％未満の効率は不十分であると見なされ、この電力の伝達は、可動部品やその他のコンポーネントが摩耗することなく発生します。

同じ電圧でより多くの電流を引き込むように負荷抵抗を下げると、それに応じて一次巻線を流れる電流が増加することがわかります。

AC電源が負荷抵抗に直接接続されていなくても（むしろ電磁的に「結合」されている）、電源から引き出される電流の量は、負荷が引き出される場合に引き出される電流の量とほぼ同じになります。ソースに直接接続されていました。

次の2つのSPICEシミュレーションを詳しく見て、負荷抵抗の値が異なるとどうなるかを示します。

トランスフォーマー v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0100 l2 3 5100 k l1 l2 0.999 vi1 3 4 ac 0 ** 200オームの負荷抵抗値に注意してください rload 4 5200 .ac lin 1 60 60 .print ac v（2,0）i（v1） .print ac v（3,5）i（vi1） 。終わり 

 freq v（2）i（v1） 6.000E + 01 1.000E + 01 4.679E-02 周波数v（3,5）i（vi1） 6.000E + 01 9.348E + 00 4.674E-02 

一次電流が二次電流にどのように密接に従うかに注意してください。最初のシミュレーションでは、両方の電流は約10 mAでしたが、現在は両方とも約47mAです。この2番目のシミュレーションでは、負荷電流が増加している間、磁化電流は以前と同じままであるため、2つの電流はより等しくなります。

また、負荷が重い（電流が大きい）と、二次電圧がいくらか低下することにも注意してください。さらに低い負荷抵抗値（15Ω）で別のシミュレーションを試してみましょう：

トランスフォーマー v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0100 l2 3 5100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 15 .ac lin 1 60 60 .print ac v（2,0）i（v1） .print ac v（3,5）i（vi1） 。終わり 

 freq v（2）i（v1） 6.000E + 01 1.000E + 01 1.301E-01 周波数v（3,5）i（vi1） 6.000E + 01 1.950E + 00 1.300E-01 

現在、負荷電流は0.13アンペア、つまり130 mAであり、前回よりも大幅に高くなっています。一次電流はほぼ同じですが、二次電圧が一次電圧を大幅に下回っていることに注意してください（一次電圧が10ボルトであるのに対して1.95ボルト）。

この理由は、トランスの設計に欠陥があるためです。一次インダクタンスと二次インダクタンスが完全にないためです。 リンクされている（1.000ではなく0.999のkファクター）「漂遊」または「リーク」があります 」インダクタンス。言い換えると、磁場の一部は2次コイルとリンクしていないため、エネルギーを2次コイルに結合できません:(下の図）

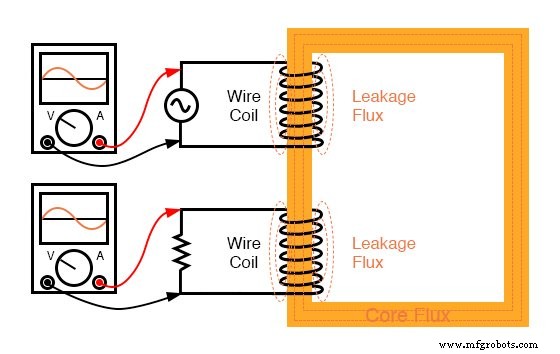
漏れインダクタンスは、磁束が両方の巻線を切断していないことが原因です。

その結果、この「漏れ」磁束は、自己インダクタンスを介してエネルギーを蓄積してソース回路に戻すだけであり、一次回路と二次回路の両方で直列インピーダンスとして効果的に機能します。この直列インピーダンスの両端で電圧が低下し、負荷電圧が低下します。負荷電流が増加すると、負荷の両端の電圧が「低下」します。 （下の図）

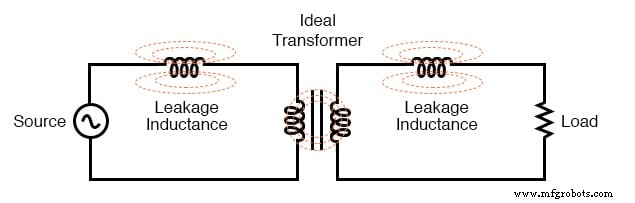
等価回路は、漏れインダクタンスを「理想的な変圧器」とは独立した直列インダクタとしてモデル化します。

一次コイルと二次コイルの間の磁気結合を改善するために変圧器の設計を変更すると、一次巻線と二次巻線の間の電圧の数値は再び等しくなります。

トランスフォーマー v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0100 l2 3 5100 **結合係数=0.999ではなく0.99999 k l1 l2 0.99999 vi1 3 4 ac 0 rload 4 5 15 .ac lin 1 60 60 .print ac v（2,0）i（v1） .print ac v（3,5）i（vi1） 。終わり 

 freq v（2）i（v1） 6.000E + 01 1.000E + 01 6.658E-01 周波数v（3,5）i（vi1） 6.000E + 01 9.987E + 00 6.658E-01 

ここでは、2次電圧が1次電圧と等しくなり、2次電流も1次電流と等しくなっていることがわかります。残念ながら、これを完全に結合して実際の変圧器を構築することは非常に困難です。

妥協案は、インダクタンスの少ない一次コイルと二次コイルの両方を設計することです。戦略は、全体としてインダクタンスが少ないと、磁気結合の非効率性がある程度ある場合に、問題を引き起こす「漏れ」インダクタンスが少なくなるというものです。これにより、同じ（高電流の重い）負荷と同じ結合係数で理想に近い負荷電圧が得られます。

トランスフォーマー v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 **インダクタンス=100ヘンリーではなく1ヘンリー l1 2 0 1 l2 3 5 1 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 15 .ac lin 1 60 60 .print ac v（2,0）i（v1） .print ac v（3,5）i（vi1） 。終わり 

 freq v（2）i（v1） 6.000E + 01 1.000E + 01 6.664E-01 周波数v（3,5）i（vi1） 6.000E + 01 9.977E + 00 6.652E-01 

インダクタンスの少ない一次コイルと二次コイルを使用するだけで、この重負荷（大電流）の負荷電圧がほぼ理想的なレベル（9.977ボルト）に戻されます。この時点で、「高負荷でほぼ理想的な性能を達成するために必要なインダクタンスが少ない場合、なぜ結合効率を心配する必要があるのでしょうか？

完全な結合を備えたトランスを構築することは不可能であるが、低インダクタンスのコイルを設計するのは簡単な場合は、低インダクタンスのコイルを備えたすべてのトランスを構築し、磁気結合が不十分な場合でも優れた効率を実現してみませんか？」

この質問に対する答えは、別のシミュレーションにあります。同じ低インダクタンスの変圧器ですが、今回は15Ωではなく1kΩの軽い負荷（電流が少ない）です。

トランスフォーマー v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 1 l2 3 5 1 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac lin 1 60 60 .print ac v（2,0）i（v1） .print ac v（3,5）i（vi1） 。終わり 

 freq v（2）i（v1） 6.000E + 01 1.000E + 01 2.835E-02 周波数v（3,5）i（vi1） 6.000E + 01 9.990E + 00 9.990E-03 

巻線インダクタンスが低くなると、一次電圧と二次電圧はほぼ等しくなりますが、一次電流と二次電流は等しくなりません。この特定のケースでは、一次電流は28.35 mAですが、二次電流はわずか9.990 mAで、一次電流は二次電流のほぼ3倍です。

どうしてこれなの？一次巻線のインダクタンスが少ないと、誘導性リアクタンスが少なくなり、その結果、磁化電流がはるかに大きくなります。一次巻線を流れるかなりの量の電流は、伝達ではなく、コアを磁化するために機能するだけです。 二次巻線と負荷への有用なエネルギー。

一次巻線と二次巻線が同一の理想的なトランスは、どの負荷条件でも、両方の巻線セットで等しい電圧と電流を示します。完璧な世界では、変圧器は、負荷が一次電源に直接接続されているかのようにスムーズに一次から二次に電力を転送します。変圧器はまったくありません。

ただし、この理想的な目標は、完璧なが存在する場合にのみ達成できることがわかります。 一次巻線と二次巻線の間の磁束の結合。これを実現することは不可能であるため、変圧器は、可能な限り理想に近い性能を発揮するために、特定の予想される電圧と負荷の範囲内で動作するように設計する必要があります。

今のところ、覚えておくべき最も重要なことは、変圧器の基本的な動作原理です。つまり、電磁結合を介した一次回路から二次回路への電力の転送です。

レビュー：

• 相互インダクタンス ここで、2つ以上のインダクタの磁束が「リンク」され、あるコイルに別のコイルの電流の変化率に比例して電圧が誘導されます。
• トランスフォーマー は、2つ以上のインダクタで構成されたデバイスであり、そのうちの1つはACから電力を供給され、2番目のインダクタの両端にAC電圧を誘導します。 2番目のインダクタが負荷に接続されている場合、電力は最初のインダクタの電源からその負荷に電磁的に結合されます。
• 変圧器の給電インダクタは一次巻線と呼ばれます 。変圧器の電力が供給されていないインダクタは、二次巻線と呼ばれます。 。
• コア内の磁束（Φ）は、ソース電圧波形より90°遅れています。この磁束を生成するためにソースから一次コイルによって引き出される電流は、磁化電流と呼ばれます。 、また、供給電圧より90°遅れます。
• 無負荷の変圧器の一次電流の合計は、励起電流と呼ばれます。 磁化電流とコア損失を克服するために必要な追加電流で構成されます。実際の変圧器では完全に正弦波になることはありませんが、磁束密度が最小に保たれるように変圧器が設計および操作されている場合は、さらに正弦波になる可能性があります。
• コア磁束は、コアに巻き付けられたコイルに電圧を誘導します。誘導電圧は、理想的には一次巻線の電源電圧と同相であり、同じ波形を共有します。
• 負荷によって二次巻線を介して引き出される電流は、一次巻線に「反射」され、電圧源が同様の負荷に直接電力を供給しているかのように電圧源から引き出されます。

関連するワークシート：

• 相互インダクタンスワークシート
• ステップアップ、ステップダウン、および絶縁トランスのワークシート