多相電力システムの高調波

混合周波数信号の章では、高調波の概念について説明しました。 ACシステムの場合：基本ソース周波数の整数倍の周波数。

AC発電機（オルタネーター）からの電源電圧波形が歪みのない単一周波数の正弦波であると想定されるAC電源システムでは、高調波成分がないはずです。 。 。理想的には。

ACシステムの非線形コンポーネント

これは、非線形コンポーネントがなければ当てはまります。 。非線形コンポーネントは、電源電圧に対して不均衡に電流を引き込み、非正弦波の電流波形を引き起こします。

非線形コンポーネントの例には、ガス放電ランプ、半導体電力制御デバイス（ダイオード、トランジスタ、SCR、トライアック）、トランス（コアのB / H飽和曲線のため、一次巻線の磁化電流は通常非正弦波）、および電気モーター（ここでも、モーターのコア内の磁場が飽和レベル近くで動作する場合）。

白熱灯でさえ、温度の急激な変動によりフィラメントの抵抗がサイクル全体で変化するため、わずかに非正弦波の電流を生成します。

混合周波数の章で学んだように、任意 それ以外の場合は正弦波形状の波形の歪みは、高調波周波数の存在を構成します。

問題の非正弦波形が平均中心線の上下で対称である場合、高調波周波数は基本波源周波数の奇数の整数倍になり、偶数の整数倍にはなりません。

ほとんどの非線形負荷はこのような電流波形を生成するため、ほとんどのAC電源システムには偶数次の高調波（2次、4次、6次、8次、10次、12次など）が存在しないか、最小限しか存在しません。

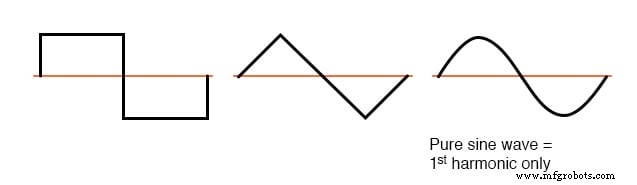
対称波形の例-奇数次高調波のみ。

偶数次高調波が存在する非対称波形の例を下の図に参照用に示します。

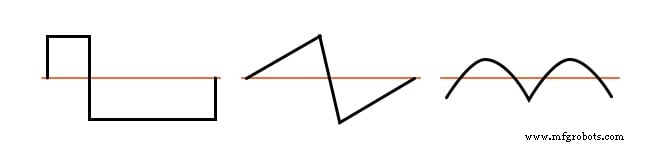
非対称波形の例—高調波も存在します。

可能な高調波周波数の半分は、非線形負荷の通常対称的な歪みによって除去されますが、奇数次の高調波は依然として問題を引き起こす可能性があります。これらの問題のいくつかは、単相またはその他のすべての電力システムに共通しています。

たとえば、渦電流損失による変圧器の過熱は、任意ので発生する可能性があります。 高調波成分が多いAC電源システム。

ただし、多相電力システムに固有の高調波電流によって引き起こされるいくつかの問題があり、このセクションで特に取り上げるのはこれらの問題です。

高調波効果に関するSPICEシミュレーション

多くの複雑な数学を回避し、調和効果をより直感的に理解するために、SPICEで非線形負荷をシミュレートできると便利です。

線形ACシステムシミュレーション

まず、非常に単純なAC回路からシミュレーションを開始します。純粋に線形の負荷と関連するすべての抵抗を備えた単一の正弦波電圧源です。

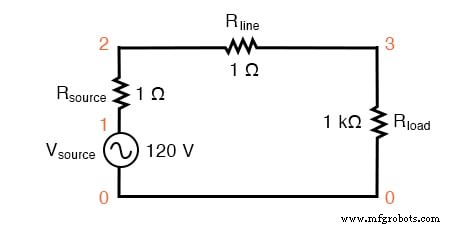
単一の正弦波ソースを備えたSPICE回路。

R _ソース およびR _line この回路の抵抗は、現実の世界を模倣するだけでなく、SPICEシミュレーションで電流を測定するための便利なシャント抵抗も提供します。1Ωの抵抗の両端の電圧を読み取ることにより、E =IRであるため、抵抗を流れる電流を直接示すことができます。 。

この回路のSPICEシミュレーション（SPICEリスト：「線形負荷シミュレーション」）と、R _line で測定された電圧のフーリエ解析 この回路のライン電流の高調波成分を表示する必要があります。本質的に完全に線形であるため、60 Hzのソースを想定すると、60 Hzの1次（基本波）以外の高調波は期待できません。

SPICEの出力「過渡応答のフーリエ成分v（2,3）」および下の図を参照してください。

線形荷重シミュレーション vsource 1 0 sin（0 120 60 0 0） rsource 1 2 1 rline 2 3 1 rload 3 0 1k .options itl5 =0 .tran 0.5m 30m 0 1u .plot tran v（2,3） .four 60 v（2,3） 。終わり 

 過渡応答のフーリエ成分v（2,3） DCコンポーネント=4.028E-12 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 5.793E-12 0.000000 51.122 123.122 3 1.800E + 02 7.407E-12 0.000000 -34.624 37.376 4 2.400E + 02 9.056E-12 0.000000 4.267 76.267 5 3.000E + 02 1.651E-11 0.000000 -83.461 -11.461 6 3.600E + 02 3.931E-11 0.000000 36.399 108.399 7 4.200E + 02 2.338E-11 0.000000 -41.343 30.657 8 4.800E + 02 4.716E-11 0.000000 53.324 125.324 9 5.400E + 02 3.453E-11 0.000000 21.691 93.691 全高調波歪み=0.000000パーセント 

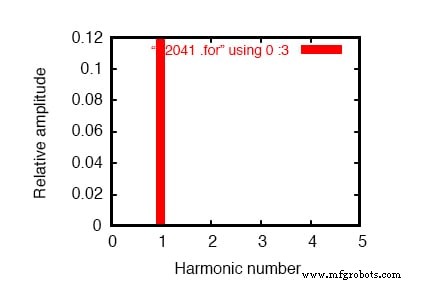
単一周波数成分の周波数領域プロット。 SPICEリスト：「線形負荷シミュレーション」を参照してください。

.plotコマンドがSPICEネットリストに表示され、通常、これにより正弦波グラフが出力されます。ただし、この場合、簡潔にするために波形表示を意図的に省略しました。.plotコマンドは、SPICEのフーリエ変換関数の癖を満たすためだけにネットリストに含まれています。

離散フーリエ変換は完全ではないため、SPICEがフーリエ解析を実行する限りの9次高調波（表）までのすべての周波数で、非常に小さな高調波電流が（ピコアンペア範囲で！）示されます。 。

1次高調波の「Fourierコンポーネント」または基本周波数に対して0.1198アンペア（1.198E-01）を示します。これは、予想される負荷電流です。電源電圧が120ボルト、負荷抵抗が1の​​場合、約120mAです。 kΩ。

単純な非線形単相ACシステムシミュレーション

次に、高調波電流を生成するために非線形負荷をシミュレートしたいと思います。これは、2つの根本的に異なる方法で行うことができます。 1つの方法は、SPICEで簡単にシミュレートできるダイオードやその他の半導体デバイスなどの非線形コンポーネントを使用して負荷を設計することです。もう1つは、負荷抵抗と並列にいくつかのAC電流源を追加することです。

後者の方法は、高調波をシミュレートするためにエンジニアに好まれることがよくあります。これは、既知の値の電流源が、非常に複雑な応答特性を持つコンポーネントよりも数学的なネットワーク解析に適しているためです。

SPICEにすべての計算作業を任せているので、半導体コンポーネントの複雑さは問題になりませんが、電流源を微調整して任意の量の電流を生成できるため（便利な機能）、次の図とSPICEリストの「非線形負荷シミュレーション」に示されている後者のアプローチを選択してください。

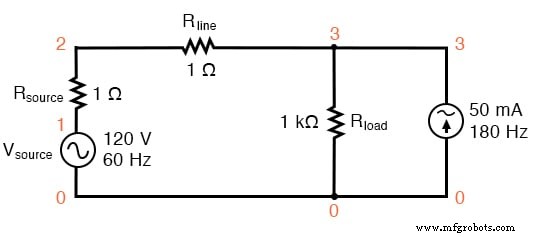
SPICE回路：3次高調波が追加された60Hzソース。

 非線形負荷シミュレーションvsource1 0 sin（0 120 60 0 0） rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin（0 50m 180 0 0） .options itl5 =0 .tran 0.5m 30m 0 1u .plot tran v（2,3） .four 60 v（2,3） 。終わり 

この回路には、50mAの大きさの電流源と180Hzの周波数があります。これは、60Hzのソース周波数の3倍です。 1kΩの負荷抵抗器と並列に接続すると、その電流が抵抗器に追加され、非正弦波の総ライン電流になります。

下の図に波形プロットを示します。これは、通常は単純な正弦波である全電流に対するこの3次高調波電流の影響を確認するためです。

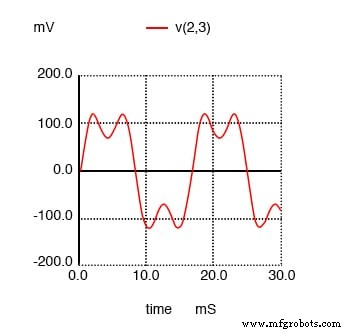
60Hzのソースと180Hzの3次高調波の合計を示すSPICE時間領域プロット。

過渡応答のフーリエ成分v（2,3） DCコンポーネント=1.349E-11 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 1.609E-11 0.000000 67.570 139.570 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2.400E + 02 1.074E-10 0.000000 -169.546 -97.546 5 3.000E + 02 3.871E-11 0.000000 169.582 241.582 6 3.600E + 02 5.736E-11 0.000000 140.845 212.845 7 4.200E + 02 8.407E-11 0.000000 177.071 249.071 8 4.800E + 02 1.329E-10 0.000000 156.772 228.772 9 5.400E + 02 2.619E-10 0.000000 160.498 232.498 全高調波歪み=41.666663パーセント 

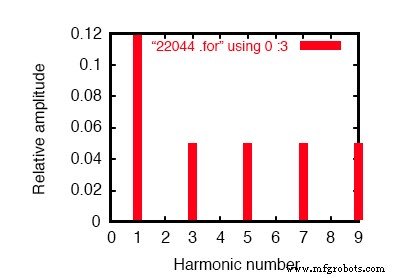
60Hzのソースと180Hzの3次高調波を示すSPICEフーリエプロット。

フーリエ解析では（上の図と「過渡応答v（2,3）のフーリエ成分」を参照）、混合周波数は混合されておらず、別々に表示されます。

ここでは、最初のシミュレーションで行ったのと同じ0.1198アンペアの60 Hz（基本）電流が表示されますが、3次高調波行に表示されるのは、49.9mAです。50mA、180Hzの電流源が動作しています。なぜ私たちはラインを通して50mA全体を見ないのですか？

その電流源は1kΩの負荷抵抗の両端に接続されているため、その電流の一部は負荷を介してシャントされ、ラインを通過してソースに戻ることはありません。これは、負荷の一部が「通常」（抵抗）であり、他の部分が電流源によって模倣される、このタイプのシミュレーションの必然的な結果です。

複数の電流源を使用した非線形単相ACシステムシミュレーション

「負荷」にさらに電流源を追加すると、理想的な正弦波形からの線電流波形の歪みがさらに見られ、それらの各高調波電流がフーリエ解析の内訳に表示されます。下の図とSPICEリスト「非線形負荷シミュレーション」を参照してください。

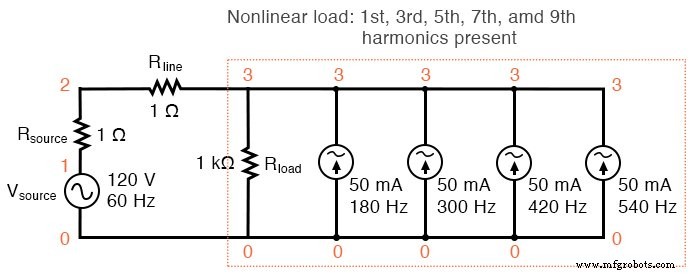
非線形負荷：1次、3次、5次、7次、および9次高調波が存在します。

非線形負荷シミュレーション vsource 1 0 sin（0 120 60 0 0） rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin（0 50m 180 0 0） i5har 3 0 sin（0 50m 300 0 0） i7har 3 0 sin（0 50m 420 0 0） i9har 3 0 sin（0 50m 540 0 0） .options itl5 =0 .tran 0.5m 30m 0 1u .plot tran v（2,3） .four 60 v（2,3）.end 

過渡応答のフーリエ成分v（2,3） DCコンポーネント=6.299E-11 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.198E-01 1.000000 -72.000 0.000 2 1.200E + 02 1.900E-09 0.000000 -93.908 -21.908 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2.400E + 02 5.469E-09 0.000000 -116.873 -44.873 5 3.000E + 02 4.990E-02 0.416667 0.000 72.000 6 3.600E + 02 6.271E-09 0.000000 85.062 157.062 7 4.200E + 02 4.990E-02 0.416666 -144.000 -72.000 8 4.800E + 02 2.742E-09 0.000000 -38.781 33.219 9 5.400E + 02 4.990E-02 0.416666 72.000 144.000 全高調波歪み=83.333296パーセント 

フーリエ解析：「過渡応答v（2,3）のフーリエ成分」。

フーリエ解析（上の図）からわかるように、すべての高調波電流源は、それぞれ49.9mAのライン電流で等しく表されます。これまでのところ、これは単相電力システムのシミュレーションにすぎません。

三相ACシステムシミュレーション

三相シミュレーションにすると、物事はより面白くなります。 2つのフーリエ解析が実行されます。1つはライン抵抗の両端の電圧、もう1つはニュートラル抵抗の両端の電圧です。

前と同じように、それぞれ1Ωの固定抵抗の両端の電圧を読み取ると、それらの抵抗を流れる電流が直接示されます。下の図とSPICEのリスト「高調波を使用したY-Yソース/負荷4線式システム」を参照してください。

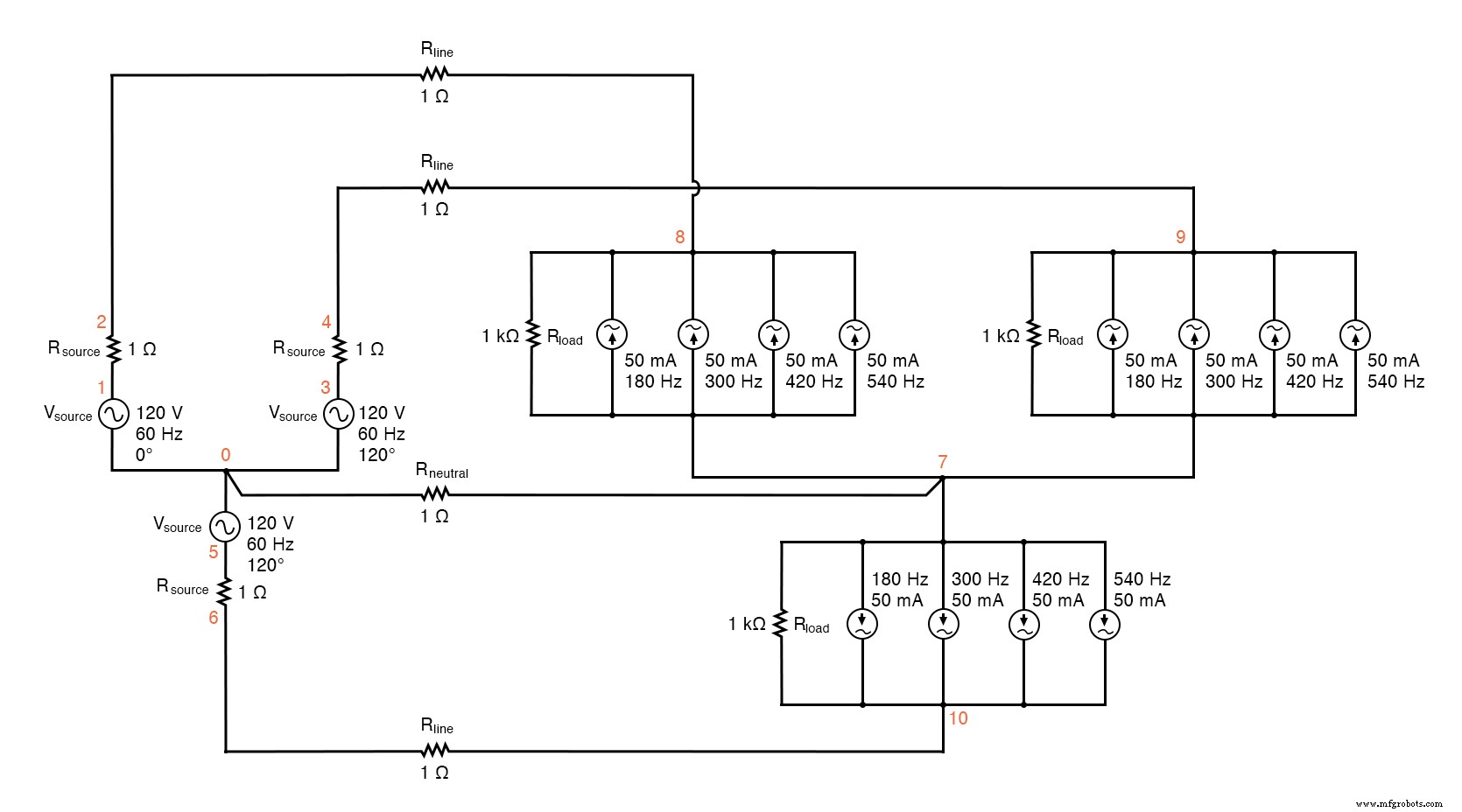
SPICE回路：「ライン電流」と「ニュートラル電流」の分析、高調波を使用したY-Yソース/負荷4線式システム。

 Y-Yソース/ロード4線式システム、高調波 * *フェーズ1電圧源およびr（120 v / _ 0度） vsource1 1 0 sin（0 120 60 0 0） rsource1 1 2 1 * *フェーズ2電圧源およびr（120 v / _ 120度） vsource2 3 0 sin（0 120 60 5.55555m 0） rsource2 3 4 1 * *フェーズ3電圧源およびr（120 v / _ 240度） vsource3 5 0 sin（0 120 60 11.1111m 0） rsource3 5 6 1 * *ラインおよびニュートラルワイヤの抵抗 rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 rneutral 0 7 1 * *負荷のフェーズ1 rload1 8 7 1k i3har1 8 7 sin（0 50m 180 0 0） i5har1 8 7 sin（0 50m 300 0 0） i7har1 8 7 sin（0 50m 420 0 0） i9har1 8 7 sin（0 50m 540 0 0） * *負荷のフェーズ2 rload2 9 7 1k i3har2 9 7 sin（0 50m 180 5.55555m 0） i5har2 9 7 sin（0 50m 300 5.55555m 0） i7har2 9 7 sin（0 50m 420 5.55555m 0） i9har2 9 7 sin（0 50m 540 5.55555m 0） * *負荷のフェーズ3 rload3 10 7 1k i3har3 10 7 sin（0 50m 180 11.1111m 0） i5har3 10 7 sin（0 50m 300 11.1111m 0） i7har3 10 7 sin（0 50m 420 11.1111m 0） i9har3 10 7 sin（0 50m 540 11.1111m 0） * *分析のもの .options itl5 =0 .tran 0.5m 100m 12m 1u .plot tran v（2,8） .four 60 v（2,8） .plot tran v（0,7） .four 60 v（0,7） 。終わり 

ライン電流のフーリエ解析：

過渡応答のフーリエ成分v（2,8） DCコンポーネント=-6.404E-12 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.198E-01 1.000000 0.000 0.000 2 1.200E + 02 2.218E-10 0.000000 172.985 172.985 3 1.800E + 02 4.975E-02 0.415423 0.000 0.000 4 2.400E + 02 4.236E-10 0.000000 166.990 166.990 5 3.000E + 02 4.990E-02 0.416667 0.000 0.000 6 3.600E + 02 1.877E-10 0.000000 -147.146 -147.146 7 4.200E + 02 4.990E-02 0.416666 0.000 0.000 8 4.800E + 02 2.784E-10 0.000000 -148.811 -148.811 9 5.400E + 02 4.975E-02 0.415422 0.000 0.000 全高調波歪み=83.209009パーセント 

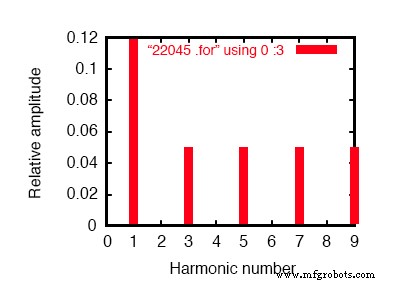
平衡Y-Yシステムにおけるライン電流のフーリエ解析。

中性カレントのフーリエ解析：

過渡応答のフーリエ成分v（0,7） DCコンポーネント=1.819E-10 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 4.337E-07 1.000000 60.018 0.000 2 1.200E + 02 1.869E-10 0.000431 91.206 31.188 3 1.800E + 02 1.493E-01 344147.7638 -180.000 -240.018 4 2.400E + 02 1.257E-09 0.002898 -21.103 -81.121 5 3.000E + 02 9.023E-07 2.080596 119.981 59.963 6 3.600E + 02 3.396E-10 0.000783 15.882 -44.136 7 4.200E + 02 1.264E-06 2.913955 59.993 -0.025 8 4.800E + 02 5.975E-10 0.001378 35.584 -24.434 9 5.400E + 02 1.493E-01 344147.4889 -179.999 -240.017 

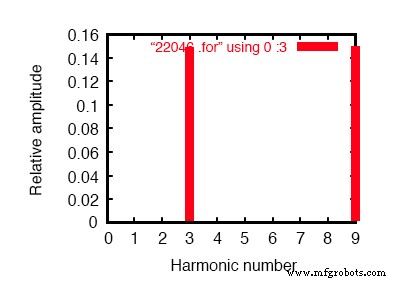
中性カレントのフーリエ解析は、高調波がないことを示しています。上の図のライン電流と比較してください。

これはバランスの取れたY-Y電力システムであり、各相は前にシミュレートした単相ACシステムと同じです。したがって、3相システムの1相の線電流のフーリエ解析が単相システムの線電流のフーリエ解析とほぼ同じであることは当然のことです。基本波（60 Hz）の線電流は0.1198アンペアおよびそれぞれ約50mAの奇数次高調波電流。

上の図とフーリエ解析を参照してください：「過渡応答のフーリエ成分v（2,8）」

ここで驚くべきことは、R _{ニュートラル}の両端の電圧降下によって決定されるニュートラル導体の電流の分析です。 SPICEノード0と7の間の抵抗。

平衡三相Y負荷では、中性電流はゼロであると予想されます。各相電流（それ自体が中性線を通ってソースYの供給相に戻る）は、すべて同じ大きさであり、すべて120°離れているため、中性線に関して互いに打ち消し合う必要があります。

調和電流のないシステムでは、これは 何が起こるか、中性線にゼロ電流を残します。

システム内の高調波電流の影響

ただし、ハーモニックについて同じことを言うことはできません。 同じシステムの電流。

基本周波数（60 Hz、または1次高調波）電流は、中性線には実質的に存在しないことに注意してください。フーリエ解析では、R _{ニュートラル}の両端の電圧を読み取ったときに、第1高調波が0.4337 µAしかないことが示されています。 。 5次および7次高調波についても同じことが言えますが、どちらの電流も無視できる大きさです。

対照的に、3次および9次高調波は中性線内で強く表され、それぞれ149.3 mA（1Ωで1.493E-01ボルト）です。これは、個別に150 mAに非常に近く、つまり電流源の値の3倍です。

負荷の高調波周波数ごとに3つのソースがあるため、各フェーズの3次および9次高調波電流が追加されているように見えます。 中性電流を形成します。フーリエ解析を参照してください：「過渡応答v（0,7）のフーリエ成分」

時間領域グラフ分析

これはまさに起こっていることですが、なぜそうなのかは明らかではないかもしれません。

これを理解するための鍵は、相電流の時間領域グラフで明らかになります。 1-2-3の相シーケンスで、時間の経過に伴う平衡相電流のこのプロットを調べます。 （下の図）

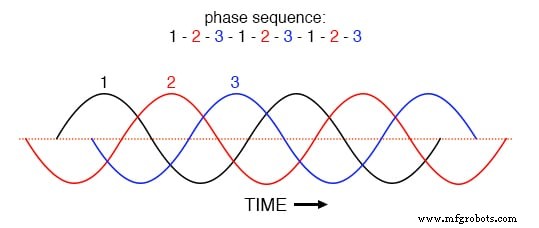
等間隔の波の位相シーケンス1-2-3-1-2-3-1-2-3。

グラフの時間軸を横切って均等にシフトされた3つの基本波形を使用すると、中性線にゼロの結果として生じる電流を与えるために、それらがどのように互いに打ち消し合うかを簡単に確認できます。ただし、フェーズ1の3次高調波波形が下の図のグラフに重ねて表示される様子を考えてみましょう。

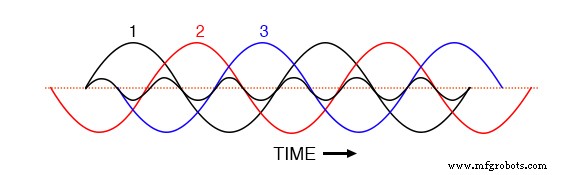
三相基本波形に重ね合わせた第1相の3次高調波波形。

この高調波波形が、2番目と3番目の基本波形と1番目の基本波と同じ位相関係にあることを確認します。任意のの各正の半サイクルで 基本波形のうち、高調波波形の正の半サイクルが2つ、負の半サイクルが1つあります。

これが意味するのは、3つの120°位相シフトされた基本周波数波形の3次高調波波形が実際には同相であるということです。 お互いに。三相ACシステムで一般的に想定される120°の位相シフトの数値は、基本周波数にのみ適用され、高調波の倍数には適用されません！

3つの3次高調波波形すべてを同じグラフにプロットすると、それらが正確に重なり合い、単一の統一された波形として表示されます（下の図に太字で示されています）

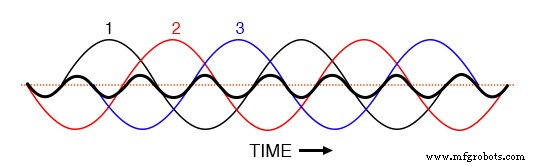
基本波の3相波形に重ね合わせると、フェーズ1、2、3の3次高調波はすべて一致します。

時間領域グラフの数学的分析

より数学的に傾いている場合、この原理は象徴的に表現されるかもしれません。 A 1つの波形を表し、 B もう1つは、両方とも同じ周波数ですが、位相に関して互いに120°シフトしています。各波形の3次高調波を A 'と呼びましょう および B ’ それぞれ。

A ’間の位相シフト および B ’ 120°ではありません（つまり、 A 間の位相シフトです および B ）、ただしその3倍、 A ’ および B ’ 波形は A の3倍の速さで交互になります および B 。波形間のシフトは、位相角でのみ正確に表現されます。 同じ角速度を仮定した場合。

異なる周波数の波形を関連付ける場合、位相シフトを表す最も正確な方法は、時間の観点からです。;およびタイムシフト A ’の間 および B ’ 3分の1の周波数で120°、または A ’の周波数で360°に相当します および B ’ 。 360°の位相シフトは0°の位相シフトと同じです。つまり、位相シフトはまったくありません。

したがって、 A ’ および B ’ 互いに同相である必要があります：

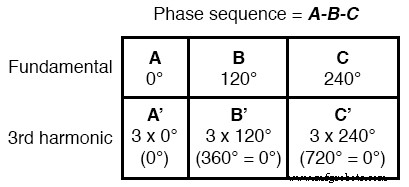
三相システムの3次高調波のこの特性は、3次高調波の整数倍にも当てはまります。

つまり、各基本波の3次高調波波形は互いに同相であるだけでなく、6次高調波、9次高調波、12次高調波、15次高調波、18次高調波、21次高調波なども同相です。

波形の歪みが中心線に対して対称であるシステムでは奇数次の高調波のみが発生し、ほとんどの非線形負荷は対称的な歪みを生成するため、3次高調波の偶数倍（6、12、18など）は一般に重要ではなく、奇数の倍数（3、9、15、21など）は、中性電流に大きく影響します。

3つ以外のいくつかの相を持つ多相電力システムでは、この効果は同じ倍数の高調波で発生します。たとえば、基本波形間の位相シフトが90°であるスター接続された4相システムの中性線に追加される高調波電流は、4、8、12、16、20などになります。

トリプレンハーモニクス

三相電力システムにおけるそれらの豊富さと重要性のために、3次高調波とその倍数には独自の特別な名前があります：三重高調波 。

すべてのトリプレン高調波は、4線式Y接続負荷の中性線で互いに加算されます。実質的な非線形負荷を含む電力システムでは、三重高調波電流は、中性線を過熱させるのに十分な大きさである可能性があります。

他の安全上の懸念により中性線が過電流保護されることを禁じているため、これは非常に問題があります。したがって、これらの大電流を自動的に遮断する機能はありません。

Y-Y回路におけるトリプレン高調波の影響の分析

次の図は、負荷で生成された3次高調波電流が中性線内でどのように追加されるかを示しています。記号「ω」は角速度を表すために使用され、数学的には2πfに相当します。したがって、「ω」は基本周波数を表し、「3ω」は3次高調波を表し、「5ω」は5次高調波を表します。（下図）

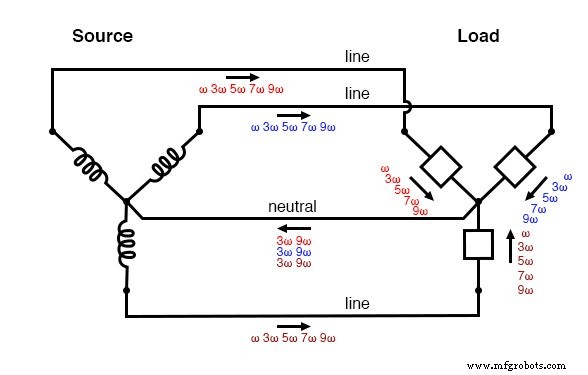
「Y-Y」トリプレンソース/負荷：高調波電流が中性線に追加されます。

これらの付加的なトリプレン電流を軽減するために、中性線を完全に取り除いたくなるかもしれません。三重電流が一緒に流れることができる中性線がない場合、それらはそうではありませんか？

残念ながら、そうすると別の問題が発生します。負荷の「Y」中心点がソースと同じ電位ではなくなります。つまり、負荷の各相は、ソースによって生成される電圧とは異なる電圧を受け取ります。

1ΩR_{ニュートラル}なしで最後のSPICEシミュレーションを再実行します 抵抗して何が起こるか見てみましょう：

 Y-Yソース/ロード（ニュートラルなし）、高調波あり * *フェーズ1電圧源およびr（120 v / 0度） vsource1 1 0 sin（0 120 60 0 0） rsource1 1 2 1 * *フェーズ2電圧源およびr（120 v / 120度） vsource2 3 0 sin（0 120 60 5.55555m 0） rsource2 3 4 1 * *フェーズ3電圧源およびr（120 v / 240度） vsource3 5 0 sin（0 120 60 11.1111m 0） rsource3 5 6 1 * *ライン抵抗 rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 * *負荷のフェーズ1 rload1 8 7 1k i3har1 8 7 sin（0 50m 180 0 0） i5har1 8 7 sin（0 50m 300 0 0） i7har1 8 7 sin（0 50m 420 0 0） i9har1 8 7 sin（0 50m 540 0 0） * *負荷のフェーズ2 rload2 9 7 1k i3har2 9 7 sin（0 50m 180 5.55555m 0） i5har2 9 7 sin（0 50m 300 5.55555m 0） i7har2 9 7 sin（0 50m 420 5.55555m 0） i9har2 9 7 sin（0 50m 540 5.55555m 0） * *負荷のフェーズ3 rload3 10 7 1k i3har3 10 7 sin（0 50m 180 11.1111m 0） i5har3 10 7 sin（0 50m 300 11.1111m 0） i7har3 10 7 sin（0 50m 420 11.1111m 0） i9har3 10 7 sin（0 50m 540 11.1111m 0） * *分析のもの .options itl5 =0 .tran 0.5m 100m 12m 1u .plot tran v（2,8） .four 60 v（2,8） .plot tran v（0,7） .four 60 v（0,7） .plot tran v（8,7） .four 60 v（8,7） 。終わり 

ライン電流のフーリエ解析：

過渡応答のフーリエ成分v（2,8） DCコンポーネント=5.423E-11 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.198E-01 1.000000 0.000 0.000 2 1.200E + 02 2.388E-10 0.000000 158.016 158.016 3 1.800E + 02 3.136E-07 0.000003 -90.009 -90.009 4 2.400E + 02 5.963E-11 0.000000 -111.510 -111.510 5 3.000E + 02 4.990E-02 0.416665 0.000 0.000 6 3.600E + 02 8.606E-11 0.000000 -124.565 -124.565 7 4.200E + 02 4.990E-02 0.416668 0.000 0.000 8 4.800E + 02 8.126E-11 0.000000 -159.638 -159.638 9 5.400E + 02 9.406E-07 0.000008 -90.005 -90.005 全高調波歪み=58.925539パーセント 

2つの「Y」中心点間の電圧のフーリエ解析：

過渡応答のフーリエ成分v（0,7） DCコンポーネント=6.093E-08 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.453E-04 1.000000 60.018 0.000 2 1.200E + 02 6.263E-08 0.000431 91.206 31.188 3 1.800E + 02 5.000E + 01 344147.7879 -180.000 -240.018 4 2.400E + 02 4.210E-07 0.002898 -21.103 -81.121 5 3.000E + 02 3.023E-04 2.080596 119.981 59.963 6 3.600E + 02 1.138E-07 0.000783 15.882 -44.136 7 4.200E + 02 4.234E-04 2.913955 59.993 -0.025 8 4.800E + 02 2.001E-07 0.001378 35.584 -24.434 9 5.400E + 02 5.000E + 01 344147.4728 -179.999 -240.017 全高調波歪み=************パーセント 

負荷相電圧のフーリエ解析：

過渡応答のフーリエ成分v（8,7） DCコンポーネント=6.070E-08 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.198E + 02 1.000000 0.000 0.000 2 1.200E + 02 6.231E-08 0.000000 90.473 90.473 3 1.800E + 02 5.000E + 01 0.417500 -180.000 -180.000 4 2.400E + 02 4.278E-07 0.000000 -19.747 -19.747 5 3.000E + 02 9.995E-02 0.000835 179.850 179.850 6 3.600E + 02 1.023E-07 0.000000 13.485 13.485 7 4.200E + 02 9.959E-02 0.000832 179.790 179.789 8 4.800E + 02 1.991E-07 0.000000 35.462 35.462 9 5.400E + 02 5.000E + 01 0.417499 -179.999 -179.999 全高調波歪み=59.043467パーセント 

確かに、奇妙なことが起こっています。

まず、負荷をソースに接続するラインでは、3次高調波電流（3番目と9番目）がほとんど消えていることがわかります。 5次および7次高調波電流は通常のレベル（約50 mA）で存在しますが、3次および9次高調波電流の大きさはごくわずかです。

次に、2つの「Y」中心点の間にかなりの高調波電圧があり、その間に中性線が接続されていたことがわかります。 SPICEによると、これら2つのポイント間には3次と9次の両方の高調波周波数が50ボルトあります。これは、線形（高調波なし）の平衡Yシステムでは明らかに正常ではありません。

最後に、負荷のフェーズの1つ（SPICE分析のノード8と7の間）で測定された電圧は、同様に、それぞれ50ボルトの強力な3次高調波電圧を示しています。

下の図は、前述の効果をグラフでまとめたものです。

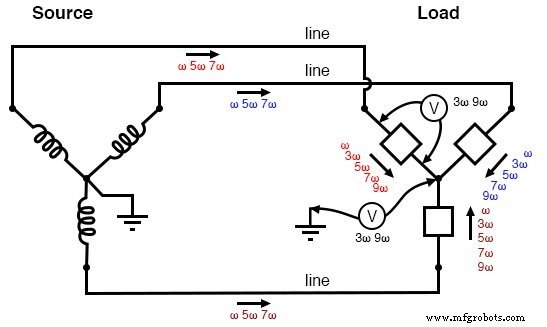
3線式「Y-Y」（ニュートラルなし）システム：「Y」中心間に三重電圧が発生します。トリプレン電圧は負荷フェーズ全体に現れます。非三重電流は線導体に現れます。

要約すると、中性線を除去すると、負荷「Y」の「ホット」な中心点が発生し、同じ大きさの高調波負荷位相電圧も発生します。これらはすべて3連周波数で構成されます。

4線式のY接続システムを使用した以前のシミュレーションでは、高調波による望ましくない影響は、過度の中性電流でした。 、ただし、少なくとも負荷の各相は、高調波がほとんどない電圧を受け取りました。

デルタ-Y（Y）回路におけるトリプレン高調波の影響の分析

中性線を取り除くことは、高調波によって引き起こされる問題を取り除くのに効果がないように思われるので、おそらくΔ構成に切り替えることでうまくいくでしょう。 Yの代わりにΔソースを試して、負荷を現在のY構成に保ち、何が起こるかを見てみましょう。

測定されるパラメータは、ライン電流（R _line の両端の電圧）になります。 、ノード0および8）、負荷相電圧（ノード8および7）、およびソース相電流（R _{ソース間の電圧} 、ノード1および2）。 （下の図）

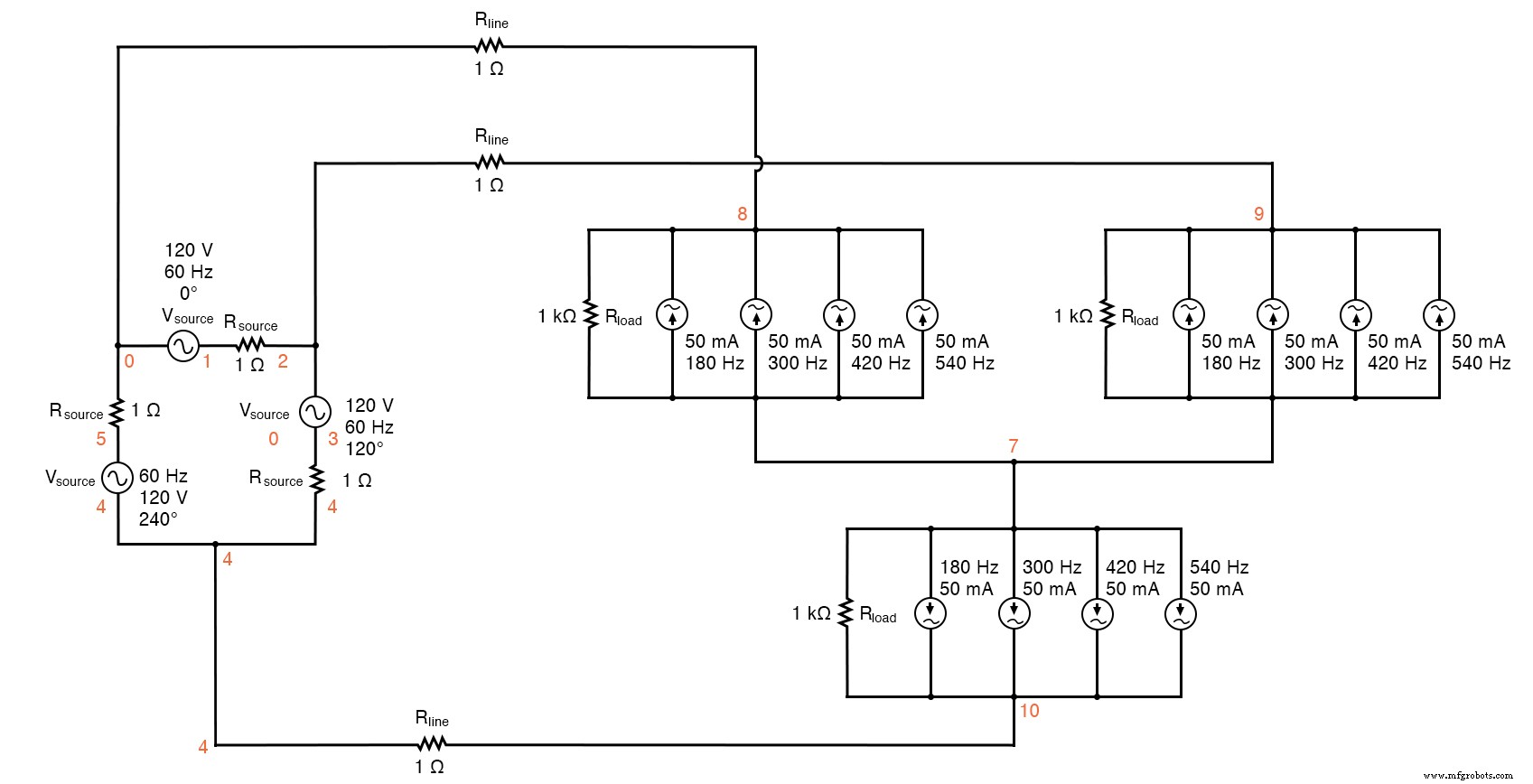
高調波を含むDelta-Yソース/ロード

高調波を含むDelta-Yソース/負荷 * *フェーズ1電圧源およびr（120 v / _ 0度） vsource1 1 0 sin（0 207.846 60 0 0） rsource1 1 2 1 * *フェーズ2電圧源およびr（120 v / _ 120度） vsource2 3 2 sin（0 207.846 60 5.55555m 0） rsource2 3 4 1 * *フェーズ3電圧源およびr（120 v / _ 240度） vsource3 5 4 sin（0 207.846 60 11.1111m 0） rsource3 5 0 1 * *ライン抵抗 rline1 0 8 1 rline2 2 9 1 rline3 4 10 1 * *負荷のフェーズ1 rload1 8 7 1k i3har1 8 7 sin（0 50m 180 9.72222m 0） i5har1 8 7 sin（0 50m 300 9.72222m 0） i7har1 8 7 sin（0 50m 420 9.72222m 0） i9har1 8 7 sin（0 50m 540 9.72222m 0） * *負荷のフェーズ2 rload2 9 7 1k i3har2 9 7 sin（0 50m 180 15.2777m 0） i5har2 9 7 sin（0 50m 300 15.2777m 0） i7har2 9 7 sin（0 50m 420 15.2777m 0） i9har2 9 7 sin（0 50m 540 15.2777m 0） * *負荷のフェーズ3 rload3 10 7 1k i3har3 10 7 sin（0 50m 180 4.16666m 0） i5har3 10 7 sin（0 50m 300 4.16666m 0） i7har3 10 7 sin（0 50m 420 4.16666m 0） i9har3 10 7 sin（0 50m 540 4.16666m 0） * *分析のもの .options itl5 =0 .tran 0.5m 100m 16m 1u .plot tran v（0,8）v（8,7）v（1,2） .four 60 v（0,8）v（8,7）v（1,2） 。終わり 

注：次の段落は、私のSPICEネットリストのすべての詳細をフォローしている好奇心旺盛な読者向けです。サーキットで何が起こっているのかを知りたいだけなら、この段落をスキップしてください！

異なる周波数と異なる位相のAC電源を持つ回路をシミュレートする場合、SPICEでそれを行う唯一の方法は、遅延時間で電源を設定することです。 または位相オフセット 秒単位で指定します。したがって、0°ソースには次の5つの指定値があります。「（0207.846 60 0 0）」は、0ボルトのDCオフセット、207.846ボルトのピーク振幅（3の平方根の120倍、負荷相電圧が各120ボルト）、60 Hz、0時間遅延、0減衰係数。

120°位相シフトされたソースには、「（0 207.846 60 5.55555m 0）」という数値があります。これは、5.55555ミリ秒の時間遅延係数、または16.6667ミリ秒の全周期の1/3を除いて、すべて最初のものと同じです。 60Hzの波形。

240°ソースは、その2倍の時間遅延が必要です。これは、240/360の16.6667ミリ秒、つまり11.1111ミリ秒に相当します。

これは、Δ接続されたソース用です。一方、Y接続負荷は、Y負荷の相電圧がΔ電源の相電圧と同相ではないため、高調波電流源に対して異なる時間遅延値のセットを必要とします。

>

Δソース電圧VAC、VBA、およびVCBがそれぞれ0°、120°、および240°で参照される場合、「Y」負荷電圧VA、VB、およびVCの位相角は-30°、90°、およびそれぞれ210°。

これはすべてのΔ-Y回路の固有の特性であり、SPICEの癖ではありません。したがって、高調波ソースの遅延時間を指定するときは、15.2777ミリ秒（-30°または+ 330°）、4.16666ミリ秒（90°）、および9.72222ミリ秒（210°）に設定する必要がありました。

>

最後に、SPICEでACソースを遅延させると、遅延時間が経過するまで「オン」になりません。つまり、その時点までの数学的分析はエラーになります。したがって、.tranトランジェント分析ラインを設定して、開始後16ミリ秒まで分析を保留します。これにより、ネットリスト内のすべてのソースが、分析が行われる前に関与する時間が与えられます。

この分析の結果は、前回とほぼ同じくらい残念です。 （下の図）ライン電流は変化せず（5次および7次高調波のみが実質的な高調波成分）、負荷相電圧も変化せず、各負荷コンポーネントに50ボルトの3次高調波（3次および9次）周波数があります。

ソース相電流はライン電流の一部であり、当然のことです。ここでは、5次と7次の両方の高調波が表されており、3次高調波はごくわずかです。

ライン電流のフーリエ解析：

 過渡応答のフーリエ成分v（0,8） DCコンポーネント=-6.850E-11 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.198E-01 1.000000 150.000 0.000 2 1.200E + 02 2.491E-11 0.000000 159.723 9.722 3 1.800E + 02 1.506E-06 0.000013 0.005 -149.996 4 2.400E + 02 2.033E-11 0.000000 52.772 -97.228 5 3.000E + 02 4.994E-02 0.416682 30.002 -119.998 6 3.600E + 02 1.234E-11 0.000000 57.802 -92.198 7 4.200E + 02 4.993E-02 0.416644 -29.998 -179.998 8 4.800E + 02 8.024E-11 0.000000 -174.200 -324.200 9 5.400E + 02 4.518E-06 0.000038 -179.995 -329.995 全高調波歪み=58.925038パーセント 

負荷相電圧のフーリエ解析：

過渡応答のフーリエ成分v（8,7） DCコンポーネント=1.259E-08 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.198E + 02 1.000000 150.000 0.000 2 1.200E + 02 1.941E-07 0.000000 49.693 -100.307 3 1.800E + 02 5.000E + 01 0.417222 -89.998 -239.998 4 2.400E + 02 1.519E-07 0.000000 66.397 -83.603 5 3.000E + 02 6.466E-02 0.000540 -151.112 -301.112 6 3.600E + 02 2.433E-07 0.000000 68.162 -81.838 7 4.200E + 02 6.931E-02 0.000578 148.548 -1.453 8 4.800E + 02 2.398E-07 0.000000 -174.897 -324.897 9 5.400E + 02 5.000E + 01 0.417221 90.006 -59.995 全高調波歪み=59.004109パーセント 

ソース相電流のフーリエ解析：

過渡応答のフーリエ成分v（1,2） DCコンポーネント=3.564E-11 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 6.906E-02 1.000000 -0.181 0.000 2 1.200E + 02 1.525E-11 0.000000 -156.674 -156.493 3 1.800E + 02 1.422E-06 0.000021 -179.996 -179.815 4 2.400E + 02 2.949E-11 0.000000 -110.570 -110.390 5 3.000E + 02 2.883E-02 0.417440 -179.996 -179.815 6 3.600E + 02 2.324E-11 0.000000 -91.926 -91.745 7 4.200E + 02 2.883E-02 0.417398 -179.994 -179.813 8 4.800E + 02 4.140E-11 0.000000 -39.875 -39.694 9 5.400E + 02 4.267E-06 0.000062 0.006 0.186 全高調波歪み=59.031969パーセント 

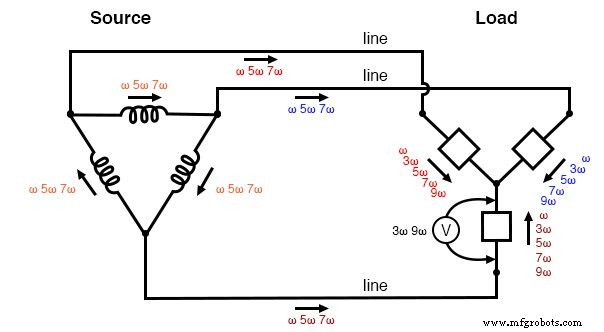
「Δ-Y」ソース/負荷：トリプレン電圧が負荷フェーズ全体に現れます。非三重電流は、線導体とソース相巻線に現れます。

実際、高調波の観点からのΔ-Y構成の唯一の利点は、負荷に衝撃の危険をもたらす中心点がなくなることです。それ以外の場合、負荷コンポーネントは同じ高調波に富む電圧を受け取り、ラインは3線式Yシステムの場合と同じ電流を受け取ります。

デルタ-デルタ回路におけるトリプレン高調波の影響の分析

システムをΔ-Δ配置に再構成する場合（下の図）、各負荷フェーズは各ソースフェーズと直接並列に接続されるため、各負荷コンポーネントが非調和電圧を受け取ることが保証されます。

Δ-Δシステムに中性線または「中心点」が完全にないため、奇妙な電圧や付加電流が発生するのを防ぎます。

それは理想的な解決策のように思われます。ライン電流、負荷相電圧、およびソース相電流をシミュレートして観察してみましょう。 SPICEリスト：「高調波を伴うデルタ-デルタソース/負荷」、「フーリエ解析：過渡応答v（0,6）のフーリエ成分」、および「過渡応答v（2,1）のフーリエ成分」を参照してください。

>

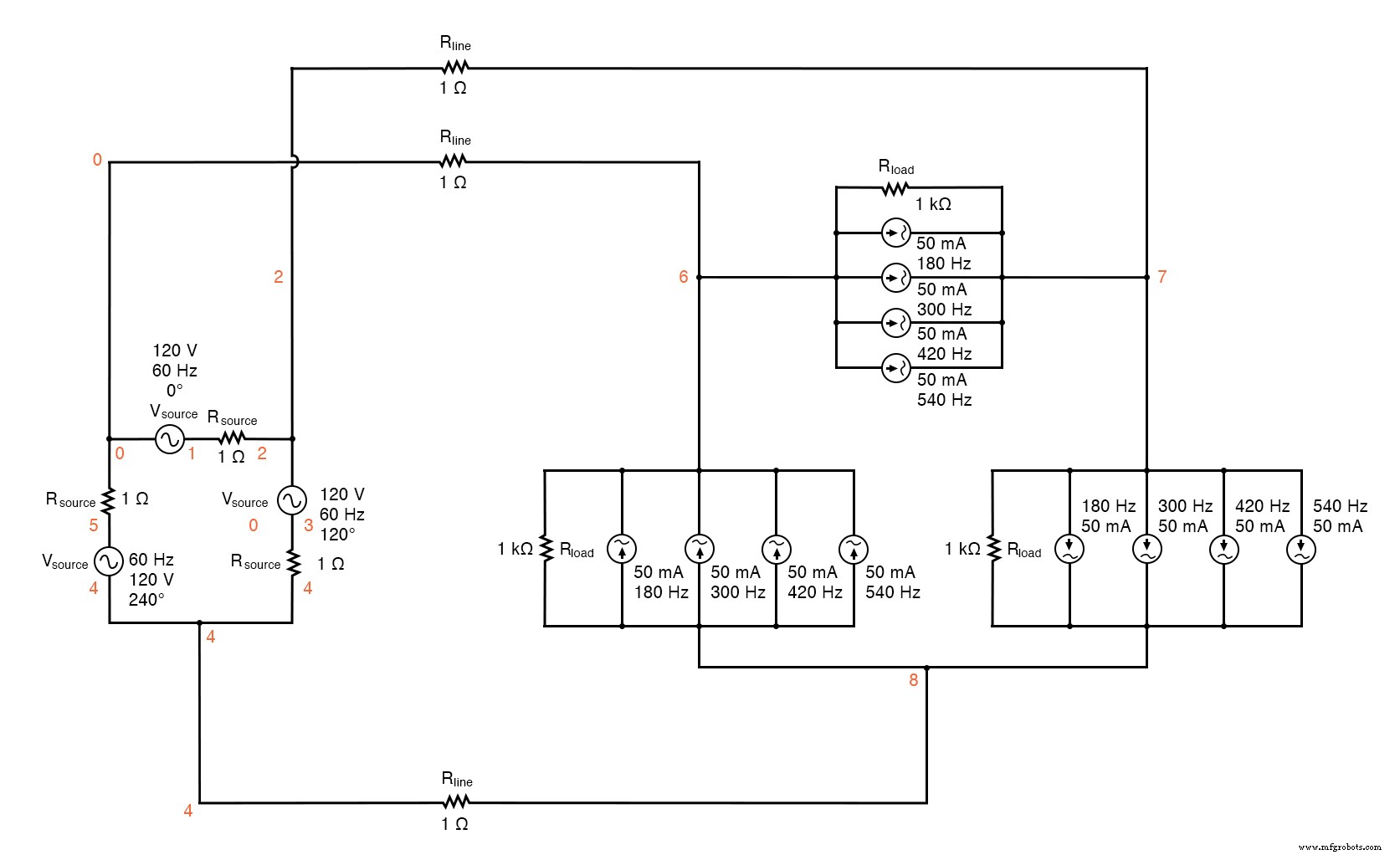
デルタ-高調波を含むデルタソース/ロード。

デルタ-高調波を含むデルタソース/負荷 * *フェーズ1電圧源およびr（120 v / _ 0度） vsource1 1 0 sin（0 120 60 0 0） rsource1 1 2 1 * *フェーズ2電圧源およびr（120 v / _ 120度） vsource2 3 2 sin（0 120 60 5.55555m 0） rsource2 3 4 1 * *フェーズ3電圧源およびr（120 v / _ 240度） vsource3 5 4 sin（0 120 60 11.1111m 0） rsource3 5 0 1 * *ライン抵抗 rline1 0 6 1 rline2 2 7 1 rline3 4 8 1 * *負荷のフェーズ1 rload1 7 6 1k i3har1 7 6 sin（0 50m 180 0 0） i5har1 7 6 sin（0 50m 300 0 0） i7har1 7 6 sin（0 50m 420 0 0） i9har1 7 6 sin（0 50m 540 0 0） * *負荷のフェーズ2 rload2 8 7 1k i3har2 8 7 sin（0 50m 180 5.55555m 0） i5har2 8 7 sin（0 50m 300 5.55555m 0） i7har2 8 7 sin（0 50m 420 5.55555m 0） i9har2 8 7 sin（0 50m 540 5.55555m 0） * *負荷のフェーズ3 rload3 6 8 1k i3har3 6 8 sin（0 50m 180 11.1111m 0） i5har3 6 8 sin（0 50m 300 11.1111m 0） i7har3 6 8 sin（0 50m 420 11.1111m 0） i9har3 6 8 sin（0 50m 540 11.1111m 0） * *分析のもの .options itl5 =0 .tran 0.5m 100m 16m 1u .plot tran v（0,6）v（7,6）v（2,1）i（3har1） .four 60 v（0,6）v（7,6）v（2,1） 。終わり 

ライン電流のフーリエ解析：

過渡応答のフーリエ成分v（0,6） DCコンポーネント=-6.007E-11 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 2.070E-01 1.000000 150.000 0.000 2 1.200E + 02 5.480E-11 0.000000 156.666 6.666 3 1.800E + 02 6.257E-07 0.000003 89.990 -60.010 4 2.400E + 02 4.911E-11 0.000000 8.187 -141.813 5 3.000E + 02 8.626E-02 0.416664 -149.999 -300.000 6 3.600E + 02 1.089E-10 0.000000 -31.997 -181.997 7 4.200E + 02 8.626E-02 0.416669 150.001 0.001 8 4.800E + 02 1.578E-10 0.000000 -63.940 -213.940 9 5.400E + 02 1.877E-06 0.000009 89.987 -60.013 全高調波歪み=58.925538パーセント 

負荷相電圧のフーリエ解析：

過渡応答のフーリエ成分v（7,6） DCコンポーネント=-5.680E-10 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.195E + 02 1.000000 0.000 0.000 2 1.200E + 02 1.039E-09 0.000000 144.749 144.749 3 1.800E + 02 1.251E-06 0.000000 89.974 89.974 4 2.400E + 02 4.215E-10 0.000000 36.127 36.127 5 3.000E + 02 1.992E-01 0.001667 -180.000 -180.000 6 3.600E + 02 2.499E-09 0.000000 -4.760 -4.760 7 4.200E + 02 1.992E-01 0.001667 -180.000 -180.000 8 4.800E + 02 2.951E-09 0.000000 -151.385 -151.385 9 5.400E + 02 3.752E-06 0.000000 89.905 89.905 全高調波歪み=0.235702パーセント 

ソース相電流のフーリエ解析：

過渡応答のフーリエ成分v（2,1） DCコンポーネント=-1.923E-12 高調波周波数フーリエ正規化位相正規化 いいえ（hz）コンポーネントコンポーネント（度）フェーズ（度） 1 6.000E + 01 1.194E-01 1.000000 179.940 0.000 2 1.200E + 02 2.569E-11 0.000000 133.491 -46.449 3 1.800E + 02 3.129E-07 0.000003 89.985 -89.955 4 2.400E + 02 2.657E-11 0.000000 23.368 -156.571 5 3.000E + 02 4.980E-02 0.416918 -180.000 -359.939 6 3.600E + 02 4.595E-11 0.000000 -22.475 -202.415 7 4.200E + 02 4.980E-02 0.416921 -180.000 -359.939 8 4.800E + 02 7.385E-11 0.000000 -63.759 -243.699 9 5.400E + 02 9.385E-07 0.000008 89.991 -89.949 全高調波歪み=58.961298パーセント 

以前に予測したように、負荷相電圧はほぼ純粋な正弦波であり、Δ-Δシステムのソース相との直接接続のおかげで、高調波成分はごくわずかです。

しかし、トリプレン高調波はどうなりましたか？ 3次および9次高調波周波数は、ライン電流にも、負荷相電圧にも、ソース相電流にも実質的な量で現れません。 3次および9次高調波電流源が意図的に負荷の相に配置されているため、3倍電流が存在することはわかっていますが、これらの電流はどこに流れましたか？

デルタ-デルタ回路におけるトリプレン高調波の影響の分析

120°位相シフトされた基本周波数の3次高調波は互いに同相であることを忘れないでください。

負荷フェーズ内の電流源の矢印が指している方向に注意し、代わりに3次および9次高調波源がDC源である場合にどうなるかを考えてください。

現在、Δ接続されたフェーズによって形成されるループ内を循環している 。これは、三重高調波電流が流れた場所です。これらは、負荷のΔ内にとどまり、線導体またはソースの巻線に到達することはありません。

これらの結果は、下の図にそのようにグラフで要約できます。

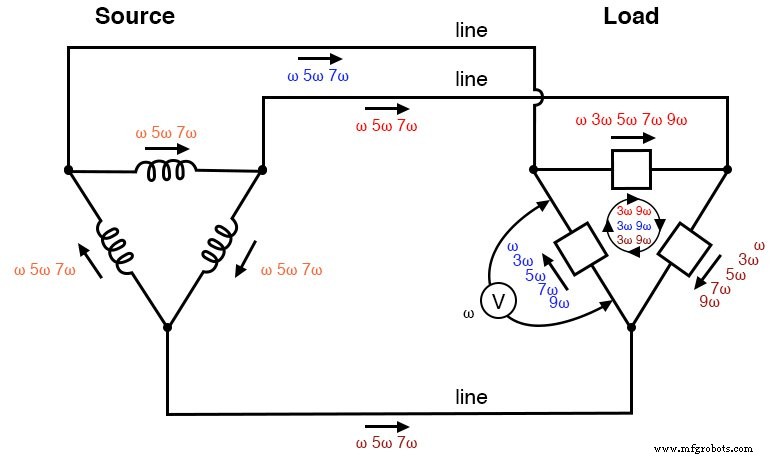
Δ-Δソース/負荷：負荷フェーズは、歪みのない正弦波電圧を受け取ります。トリプレン電流は、負荷フェーズ内を循環するように制限されています。非三重電流は、線導体とソース相巻線に現れます。

これは、Δ-Δシステム構成の主な利点です。三重高調波電流は、それらを作成するコンポーネントのセットに限定されたままであり、システムの他の部分に「拡散」しません。

レビュー：

• 非線形 コンポーネントは、正弦波（正弦波）電圧によって通電されたときに非正弦波（非正弦波）の電流波形を引き出すコンポーネントです。元々純粋な正弦波の歪みは高調波周波数を構成するため、非線形成分は高調波電流を生成すると言えます。
• 正弦波の歪みが波形の平均中心線の上下で対称である場合、存在する高調波のみが奇数番号になります。 、偶数ではありません。
• 3次高調波、およびその整数倍（6次、9次、12次、15次）は、トリプルとして知られています。 高調波。それぞれの基本波形は互いに120°位相がずれているにもかかわらず、それらは互いに同相です。
• 4線式Y-Yシステムでは、3次高調波電流が中性線内に追加されます。
• Δ接続されたコンポーネントのセット内のトリプレン高調波電流は、Δによって形成されるループ内を循環します。

関連するワークシート：

• 混合周波数信号ワークシート