ベン図とセット

数学者はベン図を使用します セットの論理的な関係を表示する （オブジェクトのコレクション）互いに。おそらく、代数や他の数学の研究でベン図を見たことがあるでしょう。持っている場合は、重なり合った円とユニオンを覚えているかもしれません。 および交差点 セットの。

ベン図の重なり合う円を確認します。デジタルエレクトロニクスで使用される用語であるため、和集合と共通部分の代わりにORとANDという用語を採用します。

ベン図は、前の章のブール代数をカルノー図にブリッジします。ブール代数についてすでに知っていることをベン図に関連付けてから、カルノー図に移行します。

セット 以下に示すように、宇宙からのオブジェクトのコレクションです。 メンバー セットのは、セット内に含まれるオブジェクトです。セットのメンバーには通常、共通点があります。ただし、これは必須ではありません。

たとえば、実数の世界から、すべての正の整数{1,2,3…}のセットがセットになります。セット{3,4,5}は、より小さなセット、つまりサブセットの例です。 すべての正の整数のセットの。別の例は、大学生の宇宙から出たすべての男性のセットです。セットの例をもう少し考えていただけますか？

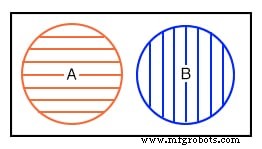
左上には、長方形の領域である宇宙U内の円の集合Aを示すベン図があります。円の内側がすべてAの場合、円の外側はAではありません。したがって、中心より上では、円Aの外側の長方形の領域にUではなくAのラベルを付けます。BとBはAではなく表示されます。同様の方法。

AとBの両方が同じ宇宙に含まれている場合はどうなりますか？ 4つの可能性を示します。

上記の4つの可能性のそれぞれを詳しく見てみましょう。

最初の例は、ベン図によると、セットAとセットBに共通点がないことを示しています。 AとBの円形のハッチング領域の間にオーバーラップはありません。たとえば、セットAとBに次のメンバーが含まれているとします。

 set A ={1,2,3,4} セットB ={5,6,7,8} 

セットAのメンバーはセットBに含まれず、BのメンバーもAに含まれません。したがって、円の重なりはありません。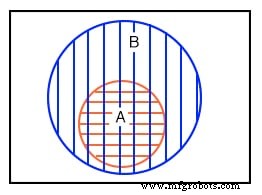

上記のベン図の2番目の例では、セットAはセットBに完全に含まれています。この状況をどのように説明できますか？セットAとBに次のメンバーが含まれているとします。

 set A ={1,2} セットB ={1,2,3,4,5,6,7,8} 

セットAのすべてのメンバーはセットBのメンバーでもあります。したがって、セットAはセットBのサブセットです。セットAのすべてのメンバーはセットBのメンバーであるため、セットAはセットBの境界内に完全に描画されます。

>

4つの例を含む5番目のケースが示されていません。ヒント：最後の（4番目の）例に似ています。この5番目のケースのベン図を描きます。

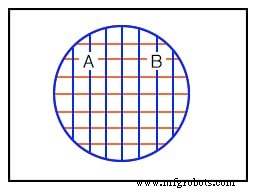
上記の3番目の例は、セットAとセットBの完全なオーバーラップを示しています。両方のセットに同じ同じメンバーが含まれているようです。セットAとBに次のものが含まれているとします。

 set A ={1,2,3,4} セットB ={1,2,3,4} 

したがって、

セットA =セットB 

セットとBは、両方とも同じメンバーを持っているため、同じです。上記の対応するベン図内のA領域とB領域は、完全に重なり合っています。上記のパターンが何を表しているのか疑問がある場合は、上または下の図を参照して、重なり合う前の円形の領域がどのようになっていたかを確認してください。

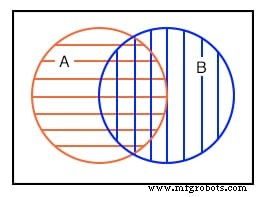
上記の4番目の例は、重複領域のセットAとセットBの間に共通点があることを示しています。たとえば、ポイントを説明するために、次のセットを任意に選択します。

 set A ={1,2,3,4} セットB ={3,4,5,6} 

セットAとセットBの両方に、共通の要素3と4があります。これらの要素が、AとBに共通する中央のオーバーラップの理由です。この状況を詳しく調べる必要があります。