粗い表面の通常の荷重による接触面積の変化：原子スケールから巨視的スケールまで

背景

ほとんどの巨視的表面は粗くフラクタルであると考えられています[1、2]。粗い表面間の接触挙動は、完全に滑らかな表面の接触挙動よりもはるかに複雑です[3、4]。実際の接触面積は、見かけの表面積よりもはるかに小さい離散接触領域（クラスター）の大きな集合によって形成されます。接触クラスターの法線力とサイズ、形状、および分布は、接触挙動を明らかにするための鍵となります。これは、摩擦に関する以下の研究に不可欠です[5,6,7]。

接触面積と荷重の関係を把握するために、1960年代から数多くのモデルが提案されてきました[1、8、9、10、11、12、13、14]。その中で、アスペリティモデルは最もシンプルで最も人気のあるモデルです。アスペリティモデルの初期のアプリケーションの1つで、GreenwoodとWilliamson [8]は、アスペリティの半径は同じで高さが異なると仮定して、接触界面の粗さを説明しています。それ以来、アスペリティモデルが普及し、この分野には膨大な量の文献が登場しています。 Whitehouse and Archard [15]は、アスペリティチップのランダムな曲率半径を考慮して、Greenwood and Williamson（G-W）モデルを開発しました。 Nayak [16,17,18]は、ランダムプロセス理論[19、20]の手法をガウス粗さの分析に導入しました。これは、その後Bush etalによって使用されました。 [9]粗い表面接触。

アスペリティモデルの基本的な仮定の1つは、アスペリティ間の相互作用を無視できることです。これは、潜在的な接触アスペリティが表面形状によって事前に決定できることを示しています。ただし、この仮定により、接触力と接触面積の推定が不正確になる可能性があります。接触するクラスターの進化とそれらの間の相互作用を取得するために、グリーン関数分子動力学（GFMD）[21,22,23]を利用して、フラクタルの粗い表面を研究します。

この作業は、通常の接触動作のために、原子スケールと巨視的スケールの間のギャップを埋めることです。原子スケールから巨視的スケールへの接触面積の進化は、アスペリティ相互作用を考慮した数値例を通して示されます。以降の説明では、最初に、フラクタル表面生成、GFMDモデル、接触クラスター検出アルゴリズム、および数値実験計画法のアプローチについて簡単に説明します。次に、接触するクラスターの形成と開発、およびこれらのプロセスがインターフェースの動作に与える影響に焦点を当てます。

メソッド

大まかなフラクタル表面の生成

粗い表面の接触挙動を研究するには、数値モデルの表面を生成する必要があります。フラクタル面にはいくつかのアルゴリズムが使用されています[24]。この作業では、図1に示すように、フーリエ変換法を使用してフラクタル粗面を生成します。フラクタル粗面のジオメトリを決定するには、4つのパラメータが必要です。これらは最大頻度です（ w _H ）、最小頻度（ w _L ）、ハースト指数（ H ）、および振幅の標準偏差（ P ）。 RMS（二乗平均平方根）高さ\（\ left（\ sqrt {M_0} \ right）\）、RMS勾配\（\ left（\ sqrt {M_2} \ right）\）、 およびRMS曲率\（\ left（\ sqrt {M_4} \ right）\）は、インターフェースの動作の主要なパラメーターです。ここで、 M _i i です 表面スペクトルの半径方向モーメント[19、20]。表面統計パラメータ M は注目に値します _i プロファイル統計パラメータ m に関連しています _i 次の式で：\（{M} _0 ={m} _0、{M} _2 =2 {m} _2、{M} _4 =\ frac {4} {3} {m} _4 \）。アスペリティ密度 n はよく知られています （表面の山または谷）は、次の式で決定できます。

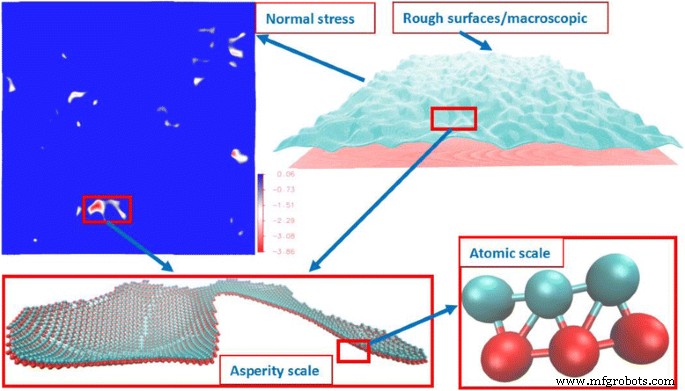
原子スケールから巨視的スケールまでのさまざまなスケールでのGFMDモデル（σ ）

さらに、表面の合計山頂/谷の数 N

ここで A ₀ は見かけの表面積です。自己アフィンフラクタル表面の場合、表面統計パラメータは入力パラメータ（ w ）に関連しています。 、 H 、 P ）次の式で：

ここで B は表面粗さ定数で、 P に関連しています。 。式（3）と（2）は、フラクタル表面の頂上/谷の数が波長とハースト指数に依存することを示しています。フラクタル表面の統計的特性の詳細な議論は、文献[25、26]にあります。

フーリエ変換アルゴリズムでは、典型的な例として、ハースト成分を H に設定します。 =0.5、最大頻度は w _L =1 /（24 σ ）、最小頻度は w _H =1 /（256 σ ）、周波数振幅の標準偏差は P =0.69、システムサイズは512×512原子（初期間隔は1.12 σ） ）。これらの入力パラメータは、その後、次の統計パラメータを使用してサーフェスを生成します：サーフェスRMS勾配\（\ sqrt {M_2} =0.077 \）およびRMS曲率\（\ sqrt {M_4} =0.0077 \）。 表面の頂上/谷の総数は、式（1）に基づいて150です。 （2）数値的に数えると、表面の山頂の数は158、谷の数は159です。誤差は5％以内であり、統計的な意味でシステムサイズが許容できることを示しています。実際、システムサイズを2048×2048原子まで増やすと（初期間隔は1.12 σに等しい） ）、統計パラメータの結果は、小規模なシステムの結果と一致しています。

GFMDモデル

粒子間の相互作用を実験的に捉えることは非常に困難です[6、27]。最近、分子動力学は、接触/摩擦メカニズムの分子起源を調査することを目的として、粒子間相互作用をシミュレートするために使用されています。ただし、大規模な分子動力学シミュレーションでは、計算コストがかなり高くなります。そのため、GFMDは、その高効率のために表面をシミュレートするために導入されました。 GFMDは、分子動力学法を使用して界面の原子（ここでは2つの層）の相互作用をシミュレートしますが、通常は弾性挙動を示す非界面層は、グリーン関数によってシミュレートされます。したがって、大きな原子系が界面で2層原子に減少し（図1を参照）、計算コストが大幅に削減されます。 GFMDの詳細な議論は、文献[21、22、23、28]で見ることができます。 GFMDモデルでは、レナードジョーンズ（LJ）ポテンシャルを使用して、粒子間の相互作用をシミュレートします。方程式は次のように記述されます

ここで、ε ポテンシャル井戸の深さ、σ は粒子間ポテンシャルがゼロになる有限距離であり、 r 粒子間の距離です。 εを取ります 、σ 、およびε / σ それぞれ、エネルギー、距離の単位、および力の単位として。 LJポテンシャルによると、 r =2 ^1/6 σ ≈1.12σ 、粒子間力はゼロです。 r の場合> 1.12 σ 、粒子間力は魅力的です。 r のとき <1.12 σ 、粒子間力は反発力です。この作業では接着を考慮していないため、カットオフ距離は1.12 σに設定されています。 。原子層に使用される結晶構造は面心立方（FCC）です。対称性があるため、図1に示すように、インターフェイスのレイヤーのみを使用してサーフェスジオメトリを形成し、平面の下の弾性ブロックをグリーン関数でシミュレートします。

クラスター認識方法への連絡

図1に示すように、インターフェースで観察される3つのスケールがあります。（1）原子スケール。LJポテンシャルによってシミュレートされます。 （2）接触原子のグループ効果であるアスペリティスケール。 （3）接触クラスターのグループ効果である巨視的スケール。接触クラスターのサイズ、形状、位置、および分布は、分子の挙動と界面特性の間の重要な橋渡しです。ナノスケールでは、原子接触領域を定義することは困難です[6]。ここでは、通常の成分力fz> 0によって接触原子を定義します。続いて、接続された接触原子は接触クラスターとして定義されます。ラベル付け手法[29、30]は、接触しているクラスターを検索するために使用されます。ここでは、再帰的な検索プロセスを回避する、加速のための修正されたアルゴリズムを使用します。アルゴリズムのフローチャートを図2に示します。ここでは、原子間力データがグリーン関数の分子動力学シミュレーションから抽出されています。アルゴリズムは、次のように8つの主要なステップに分かれています。

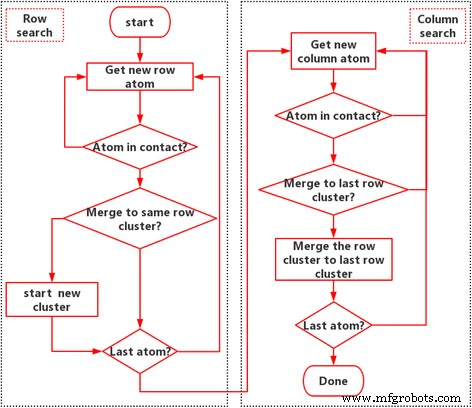
接触クラスター検出アルゴリズム：ラベリング手法

手順1.行検索を開始し、新しい原子データを取得します。つまり、行から行へと原子を検索します。

ステップ2.原子が接触しているかどうかを確認します。接触していない場合は、手順1に戻ります。接触している場合は、次の手順に進みます。

ステップ3.現在の原子を同じ行の前の原子と比較します。前の原子も接触している場合は、前の原子が属するクラスターに原子をマージしてから、前の原子と同じ番号で原子にラベルを付けます。前の原子が接触していない場合は、前の番号に1を加えた新しい番号で原子にラベルを付けます。

ステップ4.それが最後のアトムであるかどうかを判別します。そうでない場合は、ステップ1に戻るか、列検索プロセスに進みます。

ステップ5.列検索を開始し、新しい原子データを取得します。つまり、列から列へと原子を検索します。

ステップ6.原子が接触しているかどうかを確認します。接触していない場合は、手順5に戻ります。接触している場合は、次の手順に進みます。

ステップ7.現在の原子を同じ列の前の原子と比較します。前のアトムも接触していて別のクラスターに属している場合は、現在のクラスターを前のアトムが属するクラスターにマージしてから、同じ番号でアトムにラベルを付けて保存します。前の原子が接触していないか、同じクラスターに属している場合は、次のステップに進みます。

ステップ8.現在の原子が最後の原子であるかどうかを判別します。そうでない場合は、手順5に戻るか、検索プロセスが完了します。

数値実験計画

等価弾性率 E * を導入することにより、1つの複合剛体粗面と平坦な弾性面の問題として2つの粗面接触問題を簡略化できることはよく知られています。 、これは

ここで E ₁ および E ₂ は、それぞれ上面と下面の弾性率です。簡単にするために、弾性のある滑らかな表面と接触する剛性の粗い表面を検討し、接触するクラスターの形成と発達、およびその力-面積の振る舞いを研究します。以下の説明では、上で生成されたサーフェスを使用します（上面は剛性があり、粗い（ E ） ₁ =∞）、下面は滑らかで弾力性があります（ E ₂ =3 ε / σ ³ ）） v の両方で、接触行動を研究する ₁ および v ₂ 0.5に設定されています。システムサイズは512×512原子です（初期間隔は1.12 σです。 ）、および周期境界条件は x で使用されます - y 飛行機。弾性ブロックの深さは1024原子層に設定されています（初期間隔は1.12 σに等しい ）。通常の分子動力学シミュレーションでは、システムは268,697,600個の原子で構成されます。図1に示すように、GFMDモデルでは、その数が524,288（2層の原子）に減少します。粗い表面（上部）を平らな弾性表面に徐々に押し込みます。剛体表面の荷重は、変位によって制御されます。各変位荷重ステップは0.01 σに設定されます 、およびGFMDアルゴリズムは、原子間力が収束基準 L を満たすまで、各原子の位置を更新します。 ¹ -norm =0.01 ε/σ。 無限ループを回避するために、最大反復回数は50,000に設定されています。

結果と考察

クラスターの配布と開発への連絡

アスペリティモデルは、アスペリティが球形または楕円形であると見なし、接触するアスペリティ間の相互作用を考慮しません。この作品では、アスペリティモデルで使用されるアスペリティは、上記で生成されたサーフェスから抽出されます。アスペリティモデルでは、接触する可能性のあるアスペリティは、その高さに基づいて事前にサーフェスジオメトリによって決定できます。つまり、表面の頂上/谷は、それらの高さに応じて接触クラスターとして形成されます。ただし、実際には、アスペリティは不規則な形状をしており、通常、図2に示すように、いくつかの隣接するアスペリティが大きなアスペリティに融合することがあります。最初に、接触力として6つの独立したアスペリティがあることが観察されます。増加すると、最終的に大きな接触クラスターに統合されます（図3）。これは、アスペリティ間の距離が、アスペリティが互いに影響を及ぼさないように十分に遠いという仮定が、不正確な結果につながる可能性があることを示唆しています。

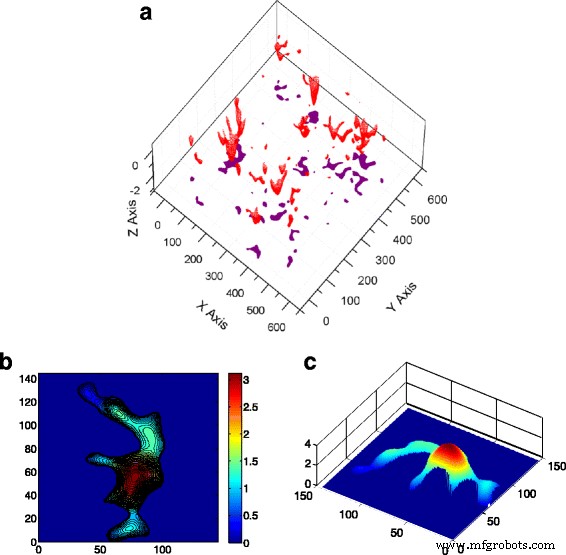
クラスターの形状とマージ効果。 a 接触クラスターの3Dビューと x への投影 - y 平面（σ内 ）。 b 6つの独立したアスペリティで構成される典型的なコンタクトクラスター。 c コンタクトクラスタのジオメトリの3Dビュー（σ内） ）

図4は、接触面積が増加するとクラスター数が最初に増加し、次に減少するのに対し、接触面積が増加すると表面の凹凸が常に増加することを示しています。これは、図3で説明されているマージ効果によるものです。

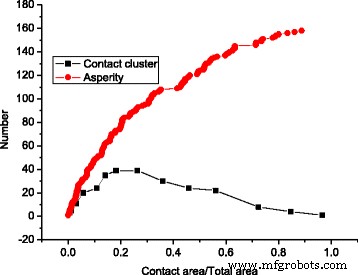
異なる接触領域での表面の谷とクラスター数

接触クラスターのマージ効果は、アスペリティモデルとGFMDモデルの両方で観察されています。ただし、同じ接触面積では、図5に示すように、GFMDモデルの接触クラスター数はアスペリティモデルの接触クラスター数よりもはるかに大きくなります。GFMDモデルの接触クラスター数は、そのほぼ2倍であることが観察されます。図5に示すように、アスペリティモデルでは、これの主な理由は、アスペリティモデルがアスペリティ間の相互作用を考慮していないことです。ただし、GFMDモデルでは、接触クラスターは相互に影響を及ぼします。接触クラスターによって生成された変位場は、表面積全体にわたって連続しています。クラスターの大きな集合の変位は、弾性表面上に新しい形状をもたらし、これは新しい接触クラスターの形成に影響を及ぼします。したがって、接触クラスターの形成は、剛性の粗い表面の高さに基づくだけでなく、滑らかな弾性表面の変形によっても影響を受ける可能性があります。これは、図6でも確認できます。この図は、アスペリティモデルとGFMDモデルのそれぞれのさまざまな領域での接触クラスターの分布を示しています。図6に示すように、接触面積が5％の場合、接触クラスター数はアスペリティモデルとGFMDモデルでそれぞれ17と34ですが、接触面積が10％の場合、接触クラスター数は24と52になります。 、 それぞれ。これは、GFMDモデルの接触クラスターがアスペリティモデルの接触クラスターよりも離散的であることを示唆しています。 GFMDモデルでは、平均クラスターサイズは小さくなりますが、図7に示すように、ほとんどのクラスターは山頂/谷と一致します。さらに、アスペリティモデルは、谷または山頂のいずれかを潜在的なアスペリティと見なします（どちら側が接触しているかによって異なります）。ただし、図8では、接触面積が大きくなると、山頂と谷の両方が接触する可能性があることがわかりました。図8では、接触面積が小さい場合、接触するほとんどの凹凸は表面の谷です。ただし、接触面積が表面積の10％を超えると、接触クラスターとして形成される山頂も増える可能性があります。

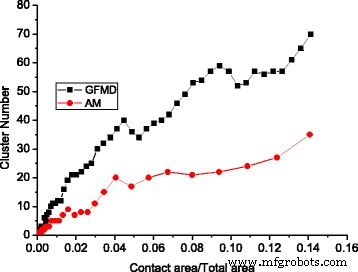
さまざまなモデルのクラスター開発

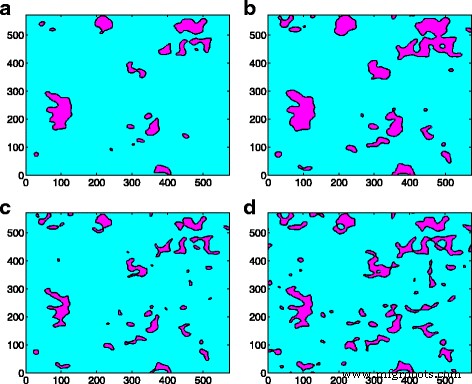
クラスター分布の等高線（σ ）それぞれ、アスペリティモデルとGFMDモデルの異なる接触領域で。 a 接触面積が5％のアスペリティモデル。 b 接触面積が10％のアスペリティモデル。 c 接触面積が5％のGFMDモデル。 d 接触面積が10％のGFMDモデル

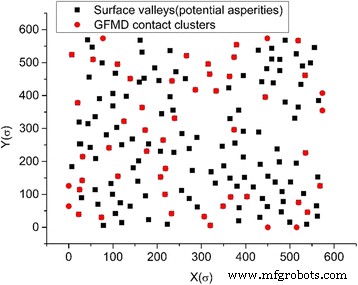
接触クラスターの位置と10％の接触面積での表面の谷

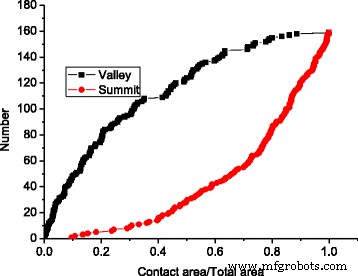
表面の谷と山頂の数は、さまざまな地域で増加しています

接触領域と荷重の関係

通常の荷重下での力と面積の関係は、接触挙動に不可欠です。以前のモデルでは、凹凸は通常、球形で楕円形であると見なされていました。ただし、実際の連絡先クラスターははるかに複雑です。このセクションでは、3つのモデルの接触力と面積の関係を比較しました。（1）GFMDモデル。 （2）アスペリティモデル（AMとマーク）。GFMDを使用してこれらのアスペリティを平らな弾性表面に押し込む前に、アスペリティを表面から直接抽出します（これにより、接触中に予期しない接触クラスターが形成されることはありません）; （3）Greenwood and Williamsonモデル（G-Wとしてマーク）。このモデルでは、アスペリティが同等の球に変換されます。球の半径は

GFMDモデルと、表面から正確に抽出されたアスペリティを使用したアスペリティモデルの場合、GFMDから抽出された各接触クラスターの力を合計することにより、インターフェイスの合計力を取得できます。 Greenwood and Williamsonモデルでは、各アスペリティ力にヘルツ理論を使用します（GFMDモデルで使用されているのと同じ材料特性を使用）。つまり、総力 F

ここで Z _i は凹凸の高さ、 d は剛体表面に適用される変位であり、 f は、ヘルツ接触理論に基づくアスペリティ接触力です。

図9では、線形関係を示す3つのモデルの力と面積の関係を比較しました。 GFMDの総力は、アスペリティモデルおよびG-Wモデルの総力よりもはるかに小さいことが観察されます。 F アスペリティモデルでは、GFMDで予測されたものの1.80倍であり、 F G-Wモデルでは、GFMDで予測された値の1.54倍です。これは、接触クラスターのRMS勾配によって説明できます。通常の負荷はRMS勾配、つまり\（L \ propto \ sqrt {M_2} \）に比例することが知られています。 GFMDモデルでは、接触面積は多数のクラスターで構成されており、その浸透はアスペリティモデルよりも浅い。アスペリティチップの勾配が小さいため、GFMDモデルの接触クラスターのRMS勾配も小さくなります。図10は、3つのモデルの接触クラスターのRMS勾配を示しています。 GFMDでの接触クラスターのRMS勾配は、表面のRMS勾配0.077よりも小さいのに対し、他の2つのモデルの接触クラスターのRMS勾配は、表面のRMS勾配よりも大きいことがわかります。

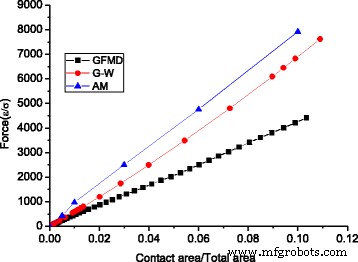
異なるモデルの接触面積と荷重の関係

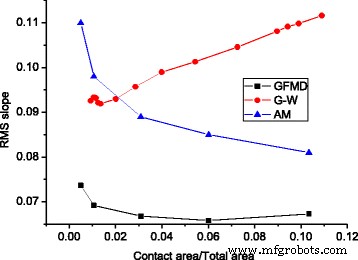
モデルごとに異なる接触面積を持つ接触クラスターのRMS勾配、表面のRMS勾配は0.077

結論

原子スケールから巨視的スケールへの接触面積の変化を見つけるために、GFMDモデルを使用して粗いフラクタル表面接触問題が研究されました。ゼロより大きい力の存在によって原子接触を定義し、同じシステムで3つの異なる長さスケールを研究しました。アスペリティ間の相互作用は、接触クラスターの形成に不可欠であることがわかります。一部のクラスターは、大きなクラスターにマージできるほど十分に接近しています。実際の接触領域は、弾性のある滑らかな表面の弾性変形により、表面の形状によって予測される領域よりもはるかに複雑です。接触クラスターの位置のほとんどは、表面の頂上/谷と一致しています。ただし、クラスターのサイズは小さく、その形成は表面の凹凸の高さによって決定されません。接触面積が増加すると、山と谷の両方が接触クラスターとして形成される可能性があります。 GFMDモデルでは、力はアスペリティモデルよりもはるかに小さく、GFMDモデルの接触クラスター数ははるかに大きくなります。 GFMDモデルの接触クラスターのRMS勾配は、アスペリティモデルのそれよりも小さいため、アスペリティモデルがより高い圧力につながる理由を説明しています。私たちの調査結果は、実際の接触面積は表面の形状だけでは予測できないことを示唆しています。通常の荷重との実際の接触面積は、以下の摩擦に関する研究にとって重要です。