ポリマーナノコンポジットのヤング率に対するナノ粒子の凝集/凝集の影響を研究するための2段階の方法論

背景

多くの研究者は、処理-構造-特性の関係における効果的なパラメータを決定し、機械的、熱的、物理的、およびバリア特性によって測定される全体的な性能を最適化するために、近年ポリマーナノコンポジットに焦点を当てています[1,2,3,4 ]。ポリマーナノコンポジット中のナノ粒子の含有量が少ないと、複合材料業界で非常に魅力的な、大きな界面面積、高弾性率、軽量、および安価な製品が生成されます。したがって、ナノ粒子の適用は、ポリマーマトリックスの性能を改善するための簡単で効率的かつ経済的な方法です。ケイ酸塩層（ナノクレイ）、カーボンナノチューブ（CNT）、およびシリカ（SiO ₂ などの無機フィラーを含むポリマーナノコンポジットの特性に対する多くの材料および処理パラメーターの影響 ）、および炭酸カルシウム（CaCO ₃ ）調査済み[5,6,7,8]。

ポリマーマトリックス中のナノ粒子のサイズと分散/分布品質は、ポリマーナノコンポジットの一般的な特性を変化させます。ファンデルワールス力や化学結合などのナノ粒子間の引力[9]や、フィラーサイズが小さくなると表面分離が大幅に減少する[10]ため、ナノ粒子は凝集して凝集する傾向があります。したがって、ナノスケールでポリマーマトリックスにナノ粒子を分散させることは困難です。凝集と凝集はどちらもナノ粒子の集合体であり、凝集には粒子の強力で高密度のコロニーが含まれますが、凝集には、機械的な力によって破壊される可能性のある緩く結合した粒子が含まれます。凝集/凝集は、フィラー含有量が高い場合に明らかであり、フィラーのナノスケールを劣化させ、ナノコンポジットに多くの欠陥と応力集中を引き起こします[11、12、13]。凝集/凝集はまた、ポリマーマトリックスとナノ粒子の間の界面面積を減少させ、ナノ粒子へのポリマー鎖の機械的関与を減少させ、硬化効果を排除します。私たちの最近の発見[14、15]とJiらの研究。機械的特性に関する[16]は、凝集/凝集がポリマーナノコンポジットのナノ粒子の硬化効果に深刻なダメージを与えることを示しています。

ナノコンポジットの実験的特性評価に加えて、構成相の特性およびナノ粒子の幾何学的形態に対する機械的挙動の依存性を定量化する理論的調査は、最近の研究において魅力的な課題をもたらしました。理論的研究は、実験結果を解明し、非常に有望なナノコンポジットの最適な合成を促進するのに役立つ可能性があります。ナノコンポジット中のナノ粒子は、隣接するマトリックスに無秩序を導入し、フィラーを取り囲む相間ゾーンの形成をもたらします。これは、バルクマトリックスやナノ粒子とは異なる特性を示します[17、18、19]。相間特性に関する理論的研究は魅力的な結果を示しており、ポリマーナノコンポジットでのナノ粒子の使用を正当化しています[20、21、22]。

ナノコンポジットの機械的性能に対する凝集/凝集の影響は、以前の研究[11、14、23、24]で調査されました。これらの研究は一般に、大きな粒子による凝集/凝集を考慮していました。最近、マルチスケールモデリング手法がナノコンポジットの特性を研究するために使用されています[25、26、27]。現在の論文では、ナノコンポジットの凝集/凝集相の割合と凝集体/凝集体のナノ粒子の部分を想定して、ポリマーナノコンポジットのヤング率におけるナノ粒子の凝集/凝集の役割を調べるために2段階の方法が提案されています。この点で、ポールとマクスウェルの2つのマイクロメカニカルモデルを適用して、ナノコンポジットのヤング率を表現します。予測を評価するために、多数の実験データが提示されています。さらに、ナノコンポジットのヤング率に対する凝集/凝集パラメータの影響が研究されています。

メソッド

ナノサイズの粒子の一部が凝集/凝集すると、ナノコンポジットのナノ粒子の不均一な分布が示されます。その結果、図1に示すように、一部のナノ粒子はマトリックス内の球状領域で凝集/凝集相と見なすことができ、その他のナノ粒子はポリマーマトリックス内に均一に分散していると見なすことができます。計算では、2つの異なるフェーズを、それぞれ球の内側と外側の領域を示す凝集/凝集フェーズと効果的なマトリックスフェーズと見なしました（図1）。

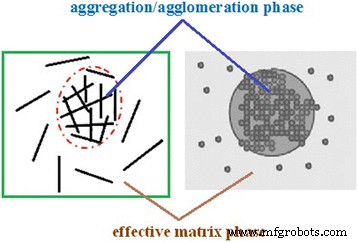
層状および球状のナノ粒子を含むポリマーナノコンポジットの凝集/凝集および効果的なマトリックス相の概略図

ポリマーナノコンポジット中のナノ粒子の凝集/凝集レベルについては、次の2つのパラメーターが推奨されます。

ここで、「 V _agg 」と「 V 」は、それぞれ凝集/凝集相とナノコンポジットの総量を示します。また、「 V _f ^agg 」と「 V _f 」は、それぞれ凝集/凝集相とナノコンポジット全体のナノ粒子の体積を示しています。凝集/凝集段階に組み込まれたナノ粒子の体積分率は、次のように表されます。

ここで、「 ϕ _f 」は、ナノコンポジット中のナノフィラーの体積分率です。また、有効なマトリックス相（凝集/凝集相から）に組み込まれた十分に分散したナノ粒子の体積分率は、次のように計算されます。

この研究では、マイクロメカニカルモデルに基づく2段階の方法論を使用して、凝集/凝集パラメータ（ z ）を決定します。 および y ）ヤング率によるポリマーナノコンポジット。まず、凝集/凝集係数と有効マトリックス相がポールのモデルによって計算されます。次に、凝集/凝集相は有効マトリックス内の球状介在物と見なされ、ナノコンポジットのヤング率は、分散粒子を含むコンポジットのマクスウェルのモデルによって計算されます。

Paul [28]は、複合材料の2つのコンポーネントの巨視的に均一な応力を次のように想定するモデルを提案しました。

ここで、「 E _m 」と「 E _f 」は、それぞれポリマーマトリックス相とフィラー相のヤング率です。最初のステップでは、凝集/凝集係数（ E _agg ）および有効行列（ E _マット ）フェーズは、「 ϕ 」を置き換えることにより、Paulのモデルによって計算されます。 _f 」と「\（{\ phi} _f ^ {agg} \）」および「\（{\ phi} _f ^ {mat} \）」を次のように使用します：

また、分散フィラーを含む複合材料のマクスウェルモデル[29]は、次の式で与えられます。

2番目のステップでは、Maxwellモデルを適用して、有効なマトリックス（マトリックスおよび十分に分散したナノ粒子）と凝集/凝集相を含む複合材料の弾性率を「 ϕ 」に置き換えて計算します。 _f 」と「 z 」（式1を参照）、「 E _f 」と凝集/凝集相の係数（ E _agg ）および「 E _m 」と有効行列の係数（ E _マット ）as：

これは、ナノコンポジットのヤング率を、骨材/凝集体の弾性率、有効マトリックス、および「z」パラメーターと相関させます。 「 E _agg 」と「 E _マット 」から7と8は後者の方程式に入力され、ナノコンポジットの弾性率は、フィラー濃度、フィラー弾性率、マトリックス弾性率、および「 z 」を使用して表されます。 」と「 y " パラメーター。ポリマーとナノ粒子の特性、およびフィラーの凝集/凝集の程度がナノコンポジットの弾性率を制御するため、弾性率のこれらのパラメーターへの依存性は合理的です。現在の方法論では、 y > z \（{VV} _f ^ {\ mathrm {agg}}> {V} _f {V} _ {\ mathrm {agg}} \）。

結果と考察

提案された方法は、PVC / CaCO ₃ を含む以前の研究からのいくつかのサンプルにおけるナノ粒子の凝集/凝集を評価するために適用されます [30]、PCL /ナノクレイ[31]、ABS /ナノクレイ[32]、PLA /ナノクレイ[33]、PET / MWCNT [34]、およびポリイミド/ MWCNT [35]。図2は、ヤング率の実験結果と2段階法の予測を示しています。計算は、さまざまなナノフィラー濃度での実験データに正しく従っており、提案された方法の正確さを示しています。ただし、ナノ粒子の凝集/凝集が適切なレベルの「 z 」によって想定される場合、実験データと理論データの間で最も高い一致が得られます。 」と「 y " パラメーター。 「 z の最高の予測 」と「 y 」パラメータは z として計算されます =0.2および y =PVC / CaCO ₃ の場合は0.95 ナノコンポジット。また、（ z 、 y ）PCL /ナノクレイ、PLA /ナノクレイ、PET / MWCNTのサンプルでは、​​それぞれ（0.3、0.75）、（0.1、0.99）、（0.35、0.7）の値が得られます。さらに、（ z 、 y ）（0.2、0.93）および（0.15、0.9）のレベルは、それぞれPET / MWCNTおよびポリイミド/ MWCNTナノコンポジットについて計算されます。これらのレベルの「 z 」と「 y 」パラメータは、言及されたナノコンポジットにおける凝集/凝集ナノ粒子の形成を示しています。これらのサンプルの弾性率のわずかな改善は、ポリマーマトリックスにおける弱い分散と高レベルのナノ粒子蓄積を確認します。たとえば、7.5 wt％のCaCO ₃ の追加 PVCに変換すると、ニートPVC（1.13 GPa）のモジュラスが1.3GPaに増加するだけです。また、PCLに10 wt％のナノクレイを組み込むと、ニートPCLの弾性率が0.22から0.37GPaに向上するだけです。ただし、ナノ粒子はポリマーマトリックスと比較して高い弾性率を示します。 CaCOのヤング率 ₃ 、ナノクレイ、およびMWCNTは、それぞれ26、180、および1000 GPa [36]と報告されていますが、現在のポリマーマトリックスのヤング率はほとんど2.5GPaに達していません。その結果、凝集/凝集したナノ粒子はナノコンポジットの弾性率を大幅に低下させ、現在の方法論は、ポリマーナノコンポジットのナノ粒子の凝集/凝集に関する許容可能なデータを示唆しています。

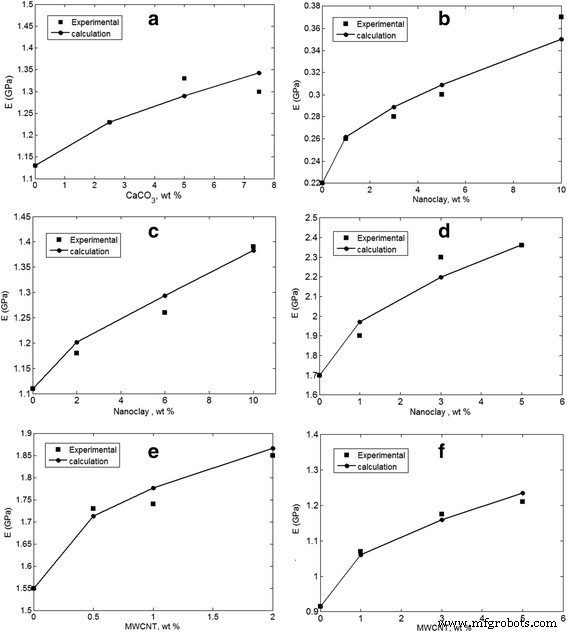
a のナノ粒子の凝集/凝集を想定した実験結果と理論結果の違い PVC / CaCO ₃ [30]、 b PCL /ナノクレイ[31]、 c ABS /ナノクレイ[32]、 d PLA /ナノクレイ[33]、 e PET / MWCNT [34]、および f ポリイミド/ MWCNT [35]サンプル

現在の方法論によって予測された最大および最小の弾性率は、平均 E で計算され、図3に示されています。 _m =2GPaおよび E _f =200GPa。最大係数は、「 z 」の最小値によって得られます。 」と「 y " パラメーター;たとえば、 z =0.00001および y =0.00001（0にすることはできません）。一方、「 y 0.99のレベルでは、すべてのナノ粒子が凝集/凝集し、弾性率が大幅に低下します。また、最高レベルの「 z 」（凝集の最大範囲）は、最小の弾性率を引き起こします。 「 z 」は、ナノコンポジット内の凝集したフィラーの体積分率がすべてのナノ粒子の体積分率よりも小さいためです（ ϕ _f ）。つまり、 z = ϕ _f わずかなレベルのモジュラスを示唆することができます。弾性率の上限値と下限値の有意差は、ナノコンポジットの剛性におけるナノ粒子の凝集/凝集の重要な役割を示しています。ナノコンポジット内のナノ粒子の凝集/凝集は、さまざまなフィラー濃度でヤング率を大幅に低下させますが、凝集/凝集のないナノ粒子の微細分散は、良好な弾性率を生成します。また、ナノフィラーの含有量が多い場合の高い凝集/凝集は、「 ϕ 」が増加すると、弾性率の成長率を低下させます。 _f 」。したがって、材料と処理パラメータを調整して、ポリマーナノコンポジットの応力集中と欠陥または剥離を促進するナノ粒子の凝集/凝集を防ぐことが重要です[37、38]。

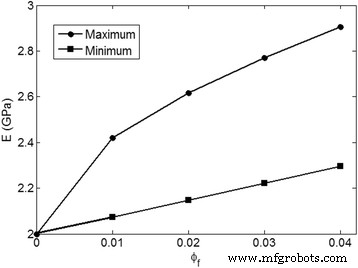
平均 E で現在の方法論によって予測された弾性率の最大および最小レベル _m =2GPaおよび E _f =200 GPa

図4は、「 z 」の効果を示しています 」と「 y 」 E での弾性率のパラメータ _m =3 GPa、 E _f =150 GPa、および ϕ _f =0.02。最高のモジュラスは、「 z 」の最小レベルで得られます。 」と「 y 」パラメータ、ナノコンポジットの弾性率に対するナノ粒子の良好な分散/分布の積極的な役割を確認します。ただし、モジュラスは「 y 」として大幅に減少します。 」パラメータが増加します。式によると。 2、「 y 」は、凝集/凝集段階でのナノ粒子の濃度を示しています。高い「 y 」では、低い弾性率が観察されます 」レベル。これは、凝集/凝集段階のナノ粒子の大部分がナノコンポジットを弱めることを示しています。したがって、凝集/凝集したナノ粒子は、ナノコンポジットの弾性率に悪影響を及ぼします。したがって、ポリマーとナノ粒子の間の界面相互作用/接着および処理パラメータに依存する、ポリマーマトリックス中のナノ粒子の分散/分布を促進するために多くの努力を払う必要があります。以前の研究では、この分野で貴重な結果が報告されており、この分散を改善するためのさまざまな手法が提案されています[39,40,41]。

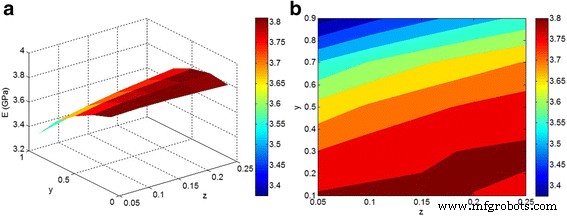
a 、 b 式による弾性率の計算。 「 z 」の関数としての10–11 」と「 y 」 E _m =3 GPa、 E _f =150 GPa、および ϕ _f =0.02

図5は、予測された係数の「 E 」への依存性を示しています。 _m 」と「 E _f 」パラメータの平均 ϕ _f =0.02、 z =0.3、および y 現在の手法では=0.5。弾性率は両方の「 E 」に依存することが観察されます _m 」と「 E _f 」は、 E が低い場合の要因 _f <150GPa。ただし、ナノ粒子の弾性率が高くても、ナノコンポジットの弾性率は変わりません。結果として、ナノコンポジットの弾性率は「 E 」にのみ依存します _m 」の場合「 E _f 」は150GPaを超えています。これは、高いナノ粒子剛性がナノコンポジットの弾性率に主要な役割を果たしていないことを示唆しており、ナノ粒子の分散/凝集/凝集に多くの注意を払う必要があります。

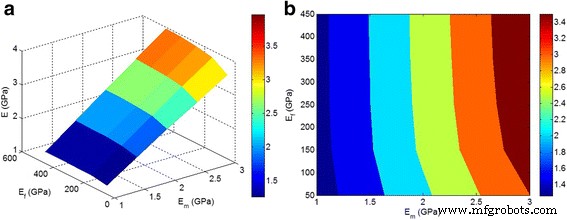
a 、 b 「 E の効果 _m 」と「 E _f 」式による予測弾性率について。平均で10〜11 ϕ _f =0.02、 z =0.3、および y =0.5

結論

ポリマーナノコンポジットのヤング率に対する凝集/凝集ナノ粒子の影響を判断するために、2段階の手法が提案されました。 PaulモデルとMaxwellモデルを適用して、凝集/凝集の係数と有効なマトリックス相を計算しました。提案された方法論の予測は、正しい凝集/凝集パラメーターを仮定して、さまざまなサンプルの実験データとの良好な一致を示しました。したがって、本方法論は、ポリマーナノコンポジットにおけるナノ粒子の凝集/凝集について許容できる結果を与えることができる。ナノ粒子の凝集/凝集はヤング率を大幅に低下させましたが、ナノ粒子の微細分散は高い弾性率を生み出しました。最小の「 z 」で最高の弾性率が得られました 」と「 y 」パラメータは、ナノコンポジットの弾性率におけるナノ粒子の良好な分散/分布の積極的な役割を確認しました。ただし、「 y 」パラメータが増加しました。さらに、高弾性率などのナノ粒子の優れた特性は、ポリマーナノコンポジットで最適な特性を達成するのに十分ではないことがわかりました。したがって、ポリマーとナノ粒子の間の界面相互作用/接着および処理パラメータに応じて、ポリマーマトリックス中のナノ粒子の分散/分布に多くの注意を向ける必要があります。