ナノ粒子の跳ね返りに及ぼす弾性剛性と表面接着の影響

背景

間違いなく、粒状力学の最も基本的なプロセスは、2つの粒子の衝突です。大きな粒子速度では、衝突後に粒子が再び分離し、衝突の結果は非弾性衝突の古典力学によって特徴付けることができます。ただし、粒子速度が小さい場合、粒子は付着します。スティッキング衝突とバウンス衝突の境界[1]は、バウンス速度 v と呼ばれることがあります。 _b 。このパラメータはナノグレインにとって特に重要であり、たとえば天体物理学で衝突ダスト凝集の説明に入るアプリケーションがあります[2、3]。

v の予測を導き出すために、巨視的な接触力学が使用されてきました _b 。これは、基本的な物理入力として弾性剛性と表面接着を使用して2つの接着球の衝突を説明するJohnson-Kendall-Roberts（JKR）理論[4]に基づいています。定量的には、これらの量は押し込み係数 E で表されます。 _ind = E /（1- ν ² ）、ここで E はヤング率であり、ν ポアソン数、および表面エネルギーγ 。球の半径 R と質量密度ρ 、2つの同一の球の跳ね返り速度は[1、5、6]を読み取ります

定数 C の値 衝突中のエネルギー散逸の仮定に強く依存し、0.3から60の間の値を仮定することが議論されています[1,7]。

この予測の妥当性は、主にそのサイズ依存性に関して研究されてきました[1、5–8]。粒子サイズが小さくなると、接着力がより重要になり、バウンド速度が増加します。実際、ナノ粒子（AgおよびNaCl粒子）の実験[9]は、 v を見つけます。 _b 粒子サイズが数10nmの場合は1m / sの範囲になりますが、小さい粒子の場合は急激に増加します。分子動力学（MD）に基づく原子シミュレーションにより、予測された R が確認されました。 ^−5/6 サイズ R のアモルファスシリカ粒子間の衝突の依存性 =15〜25 nm [7]。

これまで、 v の予測される依存関係 _b 材料パラメータについて E _ind およびγ 詳細なテストは行われていません。異なる材料は通常両方の量が異なるため、これは実験では簡単に行うことはできません。ただし、MDを使用すると、同じプロパティを持つモデルマテリアルを作成できますが、 E のいずれか1つの側面のみが異なります。 _ind またはγ 。この論文では、Cu [10]のモデルを選択しますが、材料パラメータを実際の値から最大1桁大きく変化させます。このシステムではアモルファスナノ粒子の跳ね返りがないため、結晶性（fcc）粒子に焦点を当てます。

メソッド/実験

モースポテンシャルを使用します

距離 r の2つの原子間の相互作用を説明する 。 3つのモールスパラメータ D 、α 、および r ₀ 格子定数 a を記述するために決定されます 、体積弾性率 B 、および凝集エネルギー E _coh バルクfccソリッドの。

明確にするために、格子定数を a に固定します。 この研究では=3.615Å（Cuに適切）であり、質量密度ρを維持するために、Cuの原子量も採用しています。 式で。 （1）修正済み。ポテンシャルは r で遮断されます _c =2.5 a ;したがって、合計248個の原子を含む12個の隣接するシェルが、各原子と相互作用します。 B について100個のポテンシャルが評価されます 403〜1008 GPaの範囲で、 E _coh 0.35から3.54eVの範囲で。ここで検討した体積弾性率は、実際のCu（ B ）の値よりも大きく、凝集エネルギーは小さいことに注意してください。 =134.4 GPa、 E _coh =3.54 eV [11]）、実数値の場合、バウンスは観察されなかったため。

押し込み係数 E を決定します _ind ヤング率からの（100）方向の一軸応力およびこの方向のポアソン数（[12]、p.32）。図1aは、 E の依存関係を示しています。 _ind B 。これらの量は線形関係に従うことがわかります。一定の体積弾性率では、凝集エネルギーが減少すると、 E _ind 増加します。

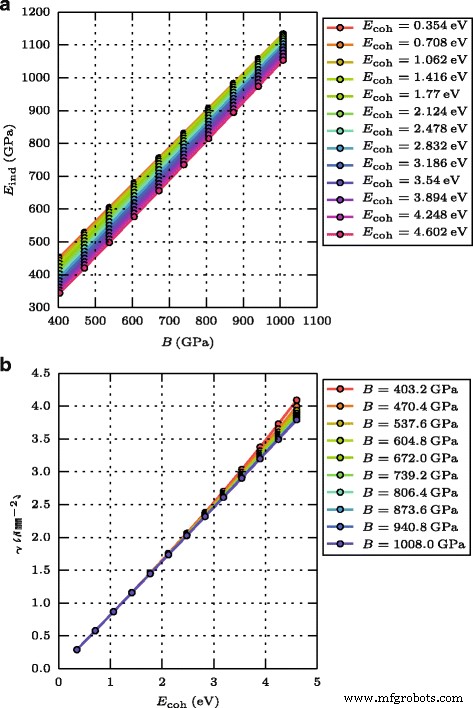
材料パラメータ。 a の依存関係 インデント係数 E _ind 体積弾性率 B および b 表面エネルギーγ 凝集エネルギーについて E _coh

（100）ファセットの表面エネルギーは、バルク結晶と開いた（100）表面を持つ結晶のエネルギー差から、開いた表面の面積で割ることによって計算されます[13]。図1bは、γを示しています。 E にほぼ比例します _coh ;偏差は、剛性が小さく、材料が強く結合している場合にのみ表示されます。

半径 R の球を切断して粒子を作成します =9 a =fcc格子から33Å、約12,000個の原子を含みます。それらの構造のために、それらはファセット表面を持っています。それらはそれらの表面を平衡化するためにリラックスしています。わずかな表面緩和が見られましたが、表面の再構築は観察されませんでした。衝突は、粒子を複製し、相対速度 v で粒子を互いに向かって発射することから始まります。 。中央衝突のみが考慮され、2つの向かい合う（100）ファセットが正面衝突します。図2を参照してください。

衝突の初期設定

跳ね返る速度を決定するために、いくつかの速度で衝突を実行します。ここで使用されるアルゴリズムは、単純な二分法に基づいています。ここで検討したすべての衝突システムで、速度250 m / sの衝突が跳ね返っていることを確認しましたが、速度が消えると衝突は発生し続けます。次に、シミュレーションは、既知の最低の跳ね返り速度と既知の最高の付着速度の算術平均で実行されます。この手順は、最高の粘着速度と最低の跳ね返り速度の差が平均値の10％未満になるまで繰り返されます。 v _b 最高の付着速度と最低の跳ね返り速度の算術平均と見なされます。後者の2つの値は、プロットでの計算のエラーを示すためにも使用されます。シミュレーションはオープンソースソフトウェアLAMMPS [14]を使用して実行され、コードはシリカ[7]と水氷粒子[15]の衝突に関する以前の研究で使用されたものと本質的に同じです。

結果

図3は、得られた結果の概要を示しています。全体的なべき乗則の適合は

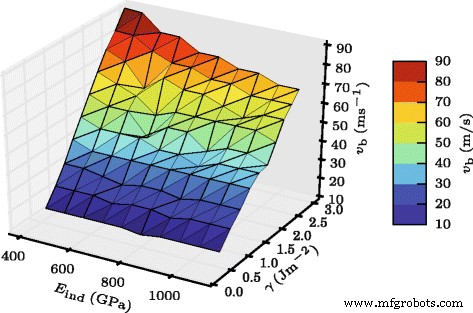
跳ね返る速度。跳ね返り速度 v の依存性の3次元プロット _b 押し込み係数 E _ind と表面エネルギーγ

したがって、JKR法の主な特徴は次のとおりです。 （1）- v の増加 _b 接着力と弾性剛性の低下が再現されますが、依存関係はJKRの場合よりも弱くなります。

図4は、これらの依存関係をより詳細に調べています。 B が固定された材料の跳ね返り速度を決定したので または E _coh 、これらの固定値について分析しますが、 E の観点から依存関係を示します _ind およびγ JKR予測と接続するために、式。 （1）。一定の凝集エネルギーの場合 E _coh 、 v _b べき乗則のように弾性剛性に依存します

跳ね返る速度。跳ね返る速度の依存性 v _b a で 押し込み弾性率 E _ind と b 表面エネルギーγ 。線はべき乗則の適合を示します。 c べき指数 a の依存関係を表示します 、式（4）、凝集エネルギーについて。線は、目をガイドする線形フィットを示します

ここで a =0.28（0.26、0.02）（ E の場合） _coh =3.54（2.12、0.35）eVしたがって、指数 a =0.33 JKRによって予測された値は、実際、高い表面エネルギーでほぼ回復しています。ただし、γが減少すると、依存関係は柔らかくなります。 粘着性の弱い表面では完全に消えます。表面エネルギーが消失する場合、すべての衝突は跳ね返る必要があることに注意してください。これは、この場合の弾性剛性の消失の役割を説明しています。

図4cは、 v の依存性のべき指数を示しています。 _b （ E _ind ）、式。 （4）、シミュレーションから得られた。プロットは、 E への依存度の増加を明確に示しています _ind 赤い線形フィットラインで示されているように、凝集エネルギー、したがって表面エネルギーが増加します。

固定弾性剛性の場合、 B 、 v の依存関係 _b γ はより簡単な図を示しています。図4cを参照してください。べき法則に適合、 v _b ∝ γ ^{− b} 、 b のかなり一貫した値を与える B の場合は=0.67（0.59、0.53） =403（739、1008）GPaであるため、 B への依存度はわずかです。 したがって、 E _ind 。ただし、これらの依存関係は b の値よりもソフトであることに注意してください。 =0.83式で予測（1）。剛性が高くなると、JKR予測からの偏差が大きくなります。確かに、JKRは硬すぎるシステムでは失敗することが知られています[16、17]。このようなシステムでは、Derjaguin-Muller-Toporov（DMT）理論[18]がより適切に適用されると考えられています。ただし、その理論からは跳ね返る速度の予測は出ていないようです。

全体として、ここで見つかった跳ね返り速度は100 m / s未満です。 Cuに適したモースポテンシャルの現実的な値については、速度の全範囲にわたって固執し、跳ね返らないことを強調します。これは、Pogorelkoらによって実行されたAl表面とのCu球（直径7〜22 nm）の衝突の最近のシミュレーションと一致しています。 [19、20] 1000 m / sの速度にこだわる人。シミュレーションでバウンスが見られる理由は、実際のCuを特徴付ける値に対して、弾性率が大幅に増加し、表面結合が減少するモデルポテンシャルを使用するためです。

バウンスしきい値を超えると、衝突は反発係数によって特徴付けられます。

衝突後の相対速度 v を比較します ^' 、衝突前のそれに、 v 、したがって、衝突の非弾性を測定します。スティッキングコリジョンの場合、明らかに e =0。 JKR理論は法則を示唆しています[4–6]

ここで、係数αを導入しました エネルギー散逸を考慮に入れる[7]。

図5は、 e の速度依存性の2つのケースを示しています。;これらは、調査した剛性と接着力の値の全範囲を代表するものであることがわかります。これらすべての場合において、衝突中の大きなエネルギー散逸はありません。 α 約0.9です。十分に大きな表面エネルギーで、図5 a、 e JKRの予測に非常によく従っています。 （6）。小さいγ ただし、図5bでは、より狭い遷移ゾーンが見られ、 e 0からほぼ1に切り替わります。この遷移ゾーンは、JKRの予測では十分に説明されていません。 （6）。

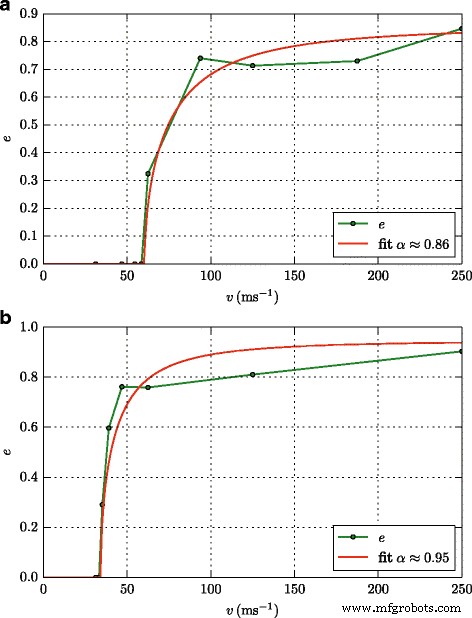
反発係数。反発係数の依存性、 e 、衝突速度について、 v 、強く（γ =2.32 J / m ² ）（ a ）そして弱く（γ =0.89 J / m ² ）（ b ）接着面。体積弾性率はどちらの場合も同じです、 B =940.8。記号はシミュレーション結果を示し、曲線はJKR予測に適合しています。 （6）、α =0.86（ a ）および0.95（ b ）

ディスカッション

スティッキングレジームでは、反発係数は1未満にとどまり、衝突中の非弾性エネルギー損失を示します。衝突中に永続的な可塑性が生成されなかったという意味で、衝突が純粋に弾性であることを確認しました。ソフトウェアツールOVITO [21]を使用して、転位の生成をチェックしました。より高速の場合、 v > 100 m / s、および順応性のある球体、転位は一時的に形成されましたが、衝突後に再び消失しました。一般的なレナードジョーンズポテンシャルを介して相互作用する同様のサイズの結晶性ナノスフェアの衝突中に、十分な転位生成を検出できた[22、23]一方で、アモルファスシリカスフィアの衝突でせん断変換ゾーンが特定されたことに注意してください[7]。したがって、衝突システムは可塑性を示します。私たちの場合、高い弾性率は塑性変形の確立を防ぎます。非弾性エネルギー損失は、衝突した球の振動の励起によってのみ引き起こされます。跳ね返る衝突の存在は、衝突中の非弾性損失の抑制、したがって塑性変形の抑制に関連していると結論付けることができます。

e の動作 小さいγの場合 v に関する上記の調査結果を強調します _b 弱接着システムでは、JKRからの大きな偏差が見られます。弱い接着の場合、バウンス速度、およびバウンス後のシステムの状態は、 E などの他のシステム特性にわずかに依存すると結論付けます。 _ind および v 。

結論

接着弾性接触のJKR理論の予測は、モデルポテンシャルを使用したナノ粒子の専用MDシミュレーションによってテストされています。材料の剛性と材料の接着力を最大1桁変化させると、跳ね返り速度の依存性の全体的な傾向がJKR理論によってかなりよく再現されることがわかります。ただし、接着力の弱い粒子には系統的な偏差が見られます。この場合、バウンスしきい値は材料の剛性に依存せず、反発係数は v を超えるとほとんど速度依存性を示しません。 _b 。また、より強い接着のために、バウンス速度のγへの依存性 JKRによって予測されたものよりも体系的に小さいです。

これらの偏差は、巨視的接触理論によるナノ粒子衝突の不完全な記述を示しています。今後の作業では、この研究を他の方向で半径が大きい結晶粒、およびアモルファス粒に拡張することを試みます。