MBiおよびMSb（M：Ti、Zr、およびHf）ハニカムにおける量子異常ホール効果の予測

背景

量子スピンホール（QSH）絶縁体などの新しい2D材料の探索に向けて、厳密な研究努力が継続的に集中されてきました。二次元トポロジカル絶縁体（2D TI）としても知られるこれらの新しい材料は、バルクシステムが絶縁体であるにもかかわらず、エッジがスピン偏極したギャップレス状態を持つという独特の特性を示します[1]。 QSH絶縁体は、スピントロニクスデバイスアプリケーションで非常に重要な散逸のないスピン/電荷輸送を示します[2]。最近、QSH絶縁体の時間反転対称性（TRS）の破れが、らせん状のエッジ状態がキラルなエッジ状態に変換される量子異常ホール効果（QAHE）システムにつながることが発見されました[3]。外部磁場を必要としない無散逸電荷輸送は、低エネルギー消費スピントロニクス[4、5]で有望なアプリケーションを提供し、より多くのQAHEシステムの探索を促しました[6、7]。 1988年にHaldaneによって予測された、QAHEは、トポロジカル絶縁体の薄膜を磁気的にドーピングすることによって2013年に実験的にのみ達成されました[8]。理論的研究により、量子異常ホール（QAH）相は、強磁性を導入し、強力なスピン軌道相互作用（SOC）効果によってバンド反転遷移を誘導することによってTIのTRSを破壊することによって達成できることが示唆されています[9、10]。したがって、QSH絶縁体は、QAHEを達成するための優れた出発材料です。いくつかの研究では、グループIV（Sn）[11–13]およびV（Bi、Sb）[6、14–17]の薄膜が、化学的機能化によっても達成できるQSH相をサポートすると予測しています[17、18]。グループIVおよびV元素に加えて、[19–21] III-Vハニカムは、自立型と機能化型の両方の場合にQSH相をサポートすることも予測されました。これらの結果は、QAHEフェーズを見つけるための道を開きました。研究によると、QAHEは機能化されたグループIV [22]およびV [17、18、22]の薄膜に存在することがわかっています。さらに、第一原理計算は、フッ素化[23]および化学的に官能化された[24] III-VハニカムのQAHEを示しています。さらに、いくつかの理論的研究は、ハニカムへの遷移金属のドーピングがQAH相を誘発する可能性があることを予測しています[17、25–27]。これは、CrおよびVドーピングによって実験的に実現されています[8、28、29]。 III-Vハニカム材料がQSH絶縁体であるという発見[19]と、磁性材料のドーピングが磁性を誘発する可能性があるという理論的予測[10]に裏付けられて、III族元素を遷移金属（M =Ti、Zr、およびHf）。遷移金属炭化物MC（M =ZrおよびHf）[30]および遷移金属ハロゲン化物MX（M =ZrおよびHf）[31]も、QSH絶縁体として存在すると予測される別の材料ファミリーです。ただし、QAHEをサポートする可能性はまだ検討されていません。これらの発見に動機付けられて、遷移金属プニクチドMPn（M =Ti、Zr、およびHf; Pn =SbおよびBi）の電子特性がQAH相を示すと予測します。この作業では、第一原理計算を使用して、遷移金属（M =Ti、Zr、およびHf）がBi / Sbハニカムに固有の磁性を誘発する能力を予測します。座屈と平面の両方のケースを調べ、ひずみによる相変化を特定します。 QAHフェーズは、チャーン数を計算し、バンドの反転を観察することによって検証されます。

結果と考察

座屈構造と平面構造の両方を採用できる純粋なBiハニカム（ユニットセルに2つの原子を持つ）と同様に、私たちの材料は、ユニットセル内の遷移金属[たとえば、Ti、Zr、およびHf]でBiの半分を置き換えることによって得られます。 1×1ユニットセルの輪郭が描かれたM-Bi / Sbの上面図を図1aに示し、座屈および平面のM-Bi / Sbハニカムの側面図をそれぞれ図1b、cに示します。対称性の高い点でラベル付けされた対応する最初のブリルアンゾーン（BZ）を図1dに示します。

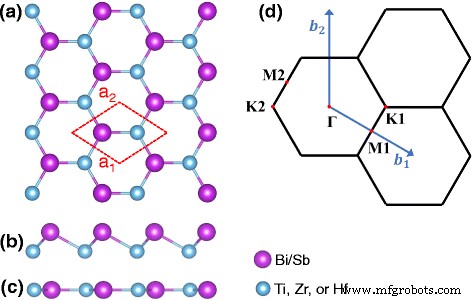
a M-Sb / Biハニカムの結晶構造。 b 、 c それぞれ座屈および平面構造の側面図。 d 対称性の高い点を持つ最初のブリルアンゾーン（BZ）

格子定数を変化させ、座屈した場合と平面の場合の両方で原子を弛緩させることにより、ハニカムの安定性とひずみの影響を研究します。次に、チャーン数の計算を通じて、さまざまな株の下でのトポロジカル相を特定しました。結果は、図2に示す状態図で示されます。TiBi、ZrBi、およびHfBiのエネルギー曲線は、それぞれ図2a〜cに示されています。 MBiハニカムは、座屈の少ない平面相を持っていることがわかりました。これらの図から、さらに分析するための平衡格子定数を特定します。この図は、座屈したMBiがエネルギー的に好まれる構造であることも示しています。ただし、ほとんどのQAH相は、ひずみが増加すると観察され、材料が座屈から平面ハニカムに変形します。また、QAH相は、座屈したHfBiで観察される可能性がありますが、格子定数の狭い範囲内でのみ観察されることに注意してください[図2cを参照]。

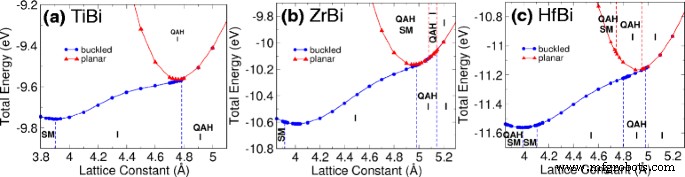
a の状態図 TiBi、 b ZrBi、および c さまざまな格子定数での総エネルギーを示すHfBi。この図は、QAH（量子異常ホール相）、I（絶縁体）、およびSM（半金属）とラベル付けされたさまざまな領域に分割されています。青い円と赤い三角形は、それぞれ座屈した場合と平面の場合を表しています

表1と表2は、M-BiおよびM-Sb構造の平衡格子定数を示しています。関連するバンドギャップ、磁気モーメント、位相、および材料の分類も示されています。 QAHEは、計算されたChern数Cがゼロ以外の整数である場合に存在します。バンドギャップは、最も低い占有バンドと最も高い占有バンドの差として計算されます。私たちの計算によると、QAH絶縁体相は、それぞれ15および7meVのバンドギャップを持つ平面TiBiおよびHfBiに見られます。さらに、座屈距離を変化させ[図3を参照]、座屈したHfBiにひずみを誘発することにより、TiBiに相転移を誘発することができます[図3]。 4]。 TiBiでは、座屈距離の変化によるバンドの交差が、図3dに示す対称性の低いポイントで発生することがわかります。 HfBiでは、最初にK2（ a ）で2つのバンド交差（臨界遷移点）を観察しました。 =4.8Å）そしてK1（ a =5.0Å）図4c、gのひずみによる。

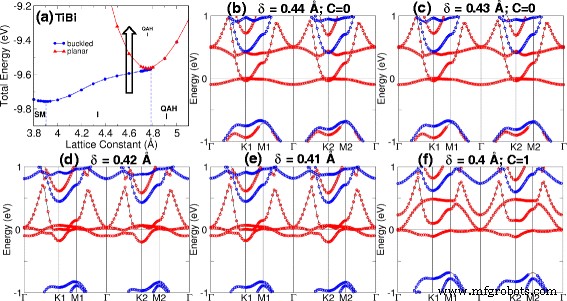
座屈距離を変化させた後の相転移。 a a でのTiBiの状態図 =4.6Å。矢印は遷移のパスを示しています。 b – f バンド構造は座屈距離（δ）として遷移します ）が0.44Åから0.4Åに減少しました。遷移はδで発生します =0.41Å

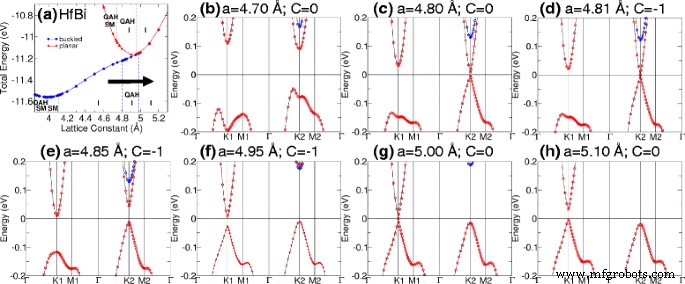
格子定数を変化させた後の相転移。 a 座屈したHfBiの状態図。矢印は遷移のパスを示しています。 b – h 格子定数が4.7から5.1Åに増加したときのバンド構造の遷移

図5a、bは、それぞれ平面構造と座屈構造のM-BiとM-Sbの平衡格子定数での電子バンド構造を示しています。赤と青の円は、それぞれスピンアップとスピンダウンの寄与です。 QAHフェーズ（ C を使用） =1）最大のバンドギャップは平面TiBiで観測された15meVです。 Planar HfBiは、7 meVの小さなバンドギャップを持つQAH絶縁体でもあります（ C =-1）。ただし、座屈した形では、HfBiは C が高い半金属です。 =−3。一方、座屈したZrBi、TiSb、ZrSb、および平面ZrSbは、些細な絶縁体であることがわかります。

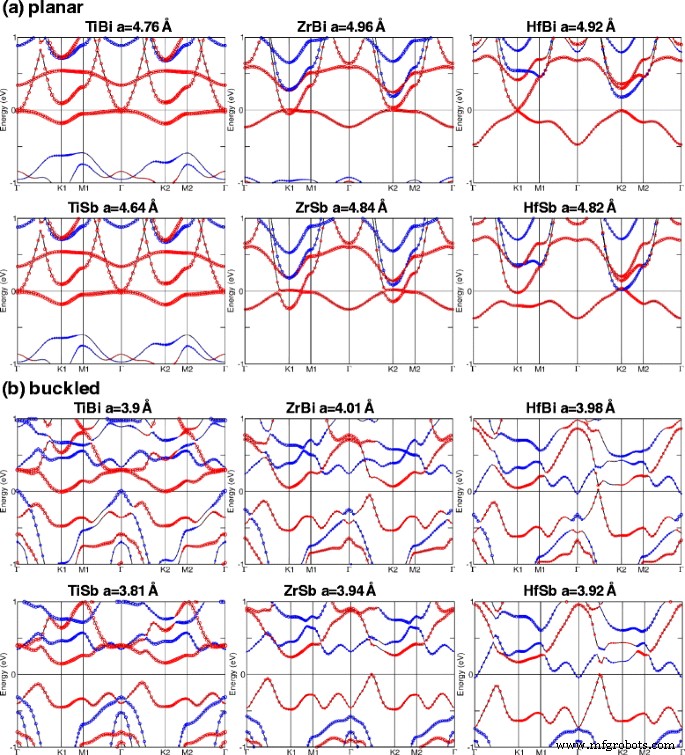
a の平衡格子定数でのM-Pn（M =Ti、Zr、およびHf; Pn =SbおよびBi）の電子バンド構造 平面および b 座屈したケース。平衡格子定数はバンド構造の上に示されています。赤と青の円は+ s を示します _z および− s _z それぞれ貢献

QAHEの性質は、非磁性および強磁性の計算におけるSOCの影響を調べることでさらに理解できます。この目的のために、平面TiBi（ a を使用）を選択しました 例として=4.76Å）。 SOCを使用した場合と使用しない場合の非磁性および強磁性の計算で得られたバンド構造を図6に示します。計算によると、この構造の磁気モーメントは1.05 μです。 _B 主にTi原子によって提供される単位格子あたり。非磁性計算では、システムが金属であることがわかります[図。 6a、c]。図6bで、遷移金属Tiの影響を受ける強磁性秩序によって正味の磁気モーメントが誘導されることがわかります。さらに、システムはギャップのないスピンアップ状態（赤い線）とギャップのあるスピンダウン状態を持ち、強磁性計算にSOCを適用することにより、15meVのギャップが得られます。これは、バンドの反転がSOCによって引き起こされ、ギャップの開口部がQAHEをもたらすことを示しています。

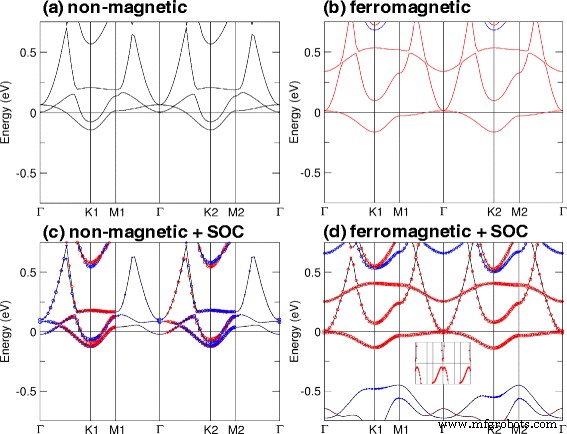
a での平面TiBiフィルムの電子バンド構造 =非磁性計算の場合は4.76Å（ a ）SOCなしおよび（ c ）SOCおよび強磁性計算（ b ）SOCなしおよび（ d ）SOCを使用。赤と青の円は+ s を示します _z および− s _z それぞれ、（ c ）非磁性（ d 強磁性）SOCによる計算

最後に、ワニエ関数を介して導出された強結合ハミルトニアンを使用して、平面HfBiハニカムのエッジバンドスペクトルにエッジ状態の存在を検査します。図7に示すように、ジグザグエッジと幅127ÅのHfBiリボンを作成しました。この図は、右エッジと左エッジをそれぞれ表す赤と青の円のサイズで示され、サイズに比例するエッジ状態の存在も確認しています。 。別々のエッジ状態は、左右のジグザグエッジの非対称性によるものです。フェルミ準位を横切る奇数のエッジバンドも観察できます。この数はチャーン数の絶対値と同じであることがわかり、平面HfBiのQAHフェーズがさらに確認されます。

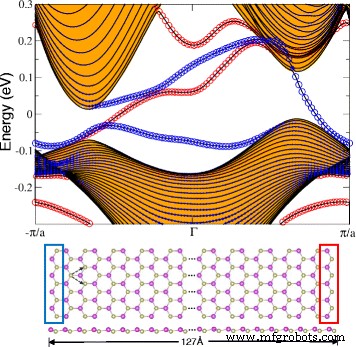
a を備えた座屈したHfBiジグザグナノリボンのエッジに沿ったバンド構造 =4.9Åおよび127Åの幅。青（赤）の円は、左（右）の端からの寄与を示します。バルクバンドはオレンジ色で塗りつぶされた領域で示されます

さらに、各システムのフォノンスペクトルを計算し、これらのシステムが負の周波数を持っていることに注目しました。したがって、前述のシステムは安定化するために基板を必要とします。また、前述の計算は1つずつユニットセルを使用して行われたものであり、強磁性（FM）構成の材料が最も安定した状態であることに注意してください。ただし、より大きなスーパーセルの場合、FMは座屈した場合の反強磁性（AFM）構成よりもエネルギーが低く、平面の場合はFMとAFMの両方の構成のエネルギーが縮退していることがわかりました。

結論

要約すると、私たちの第一原理計算は、SbまたはBiハニカム膜上の遷移金属（Ti、Zr、およびHf）の置換が潜在的にQAH相を示す可能性があることを予測しています。これらの材料は座屈した形でエネルギー的に安定していますが、それを平面状に変換すると、非常に妥当な範囲の格子定数でQAH相が生成されます。このような相は、座屈距離を変化させたり、計算された状態図のようにひずみを加えたりすることによっても誘発できます。平面TiBiおよびHfBi構造は、それぞれ15および7meVのバンドギャップを持つQAH絶縁体として存在することがわかります。これらの調査結果は、スピントロニクスアプリケーションで使用できる可能性のあるハニカム材料のQAHフェーズを実現する別の方法を提供します。

メソッド/実験

密度汎関数理論（DFT）フレームワーク内の第一原理計算は、Vienna Ab-Initio Simulationで実装されている一般化勾配近似（GGA）[32–36]およびプロジェクター拡張波（PAW）[37]法を使用して実行されました。パッケージバージョン5.3（VASP）[38、39]。運動エネルギーカットオフを350eVに設定し、残留力が5×10 ^-3 以下になるまで結晶構造を最適化しました。 eV /Å。収束の自己整合性基準は10 ^-6 に設定されました スピン軌道相互作用がある場合とない場合の電子構造計算のeV。 z に沿って少なくとも20Åの真空層を挿入することにより、薄膜をシミュレートします。 24×24×1ガンマ中心のMonkhorst-Packグリッドのサンプリングされた2Dブリルアンゾーンの方向[40]。 WANNIER90パッケージ[41]を使用して、最大にローカライズされたワニエ関数を計算し、エッジ状態の計算に使用しました。トポロジカル相は、ハイブリッドワニエ電荷中心を追跡する手法を利用するZ2Packパッケージ[42、43]を使用してチャーン数を計算することによって特定されました。