マヨラナ束縛状態にサイドカップリングされた相関量子ドットにおける熱電効果
要約
マヨラナ束縛状態(MBS)と異なる温度に保持された左右の非磁性電極に接続された量子ドット(QD)をホストするトポロジカル半導体ナノワイヤで構成されるハイブリッドデバイスの熱電効果を理論的に研究します。 QDでの電子-電子クーロン相互作用は、非平衡グリーン関数手法によって考慮されます。 MBSの検出に役立つ熱電能の符号の変化は、QD-MBS混成強度、ナノワイヤの両端のMBS間の直接重なり、およびシステム温度を変化させることによって発生することがわかります。マヨラナのキラル性により、MBSはQDの特定のスピン方向の1つの電子にのみ結合するため、QDまたは磁気電極でゼーマン分裂がない場合でも100%のスピン偏極または純粋なスピン熱電能の大きな値が現れます。フェルミオン。さらに、サーモパワーの大きさは、MBSの存在によって明らかに強化されます。
はじめに
ゼロエネルギーマヨラナ束縛状態(MBS)の準備と検出は、現代の物性物理学において特に重要です。基本的に、MBSはマヨラナフェルミ粒子のソリッドステート対応物であり、非アーベル統計に関連付けられており、デコヒーレンスのない量子計算での潜在的なアプリケーションでトポロジカルに保護された量子情報を可能にします[1–3]。これとは別に、MBSはスピントロニクスなどの高効率電子デバイスの設計にも有望です[4]。十分に分離されたMBSは、さまざまなシステムで作成できます。その中で最も重要なスキームには、非中心対称超伝導体[5]、超伝導体に結合した3次元または2次元のトポロジカル絶縁体[6]、トポロジカル超伝導体の静電欠陥[7]、 p波超伝導体[8]、従来のs波超伝導体に固有の強いスピン軌道相互作用を伴う半導体[9]または強磁性[10]ナノワイヤ、およびジョセフソン接合[11]。
MBSの検出に関しても、マヨラナフェルミ粒子はそれ自体の反粒子であり、固有の粒子-正孔対称性のために電荷に中立であるため、非常に困難です。 4 πなどの現象を通じてMBSの存在を確認するために、さまざまな実験が行われてきました。 トポロジカル超伝導体間の接合部における周期的ジョセフソン電流相[12]、トポロジカル超伝導体とトポロジカル量子異常ホール絶縁体で構成されるハイブリッド構造の強制場における半整数コンダクタンスプラトー[13]、バルクに結合されたラシュバナノワイヤを使用したトンネリング分光法-波状超伝導体[14]、およびワイヤのエッジでの微分コンダクタンスのゼロバイアス[14、15]。ただし、これらの現象には、MBSを除いて他の物理的原因が考えられるため、代替スキームが提案されています。それらの1つは、エネルギー準位、電子-電子クーロン相互作用、粒子数、および外部環境への結合強度がすべて十分に制御可能なゼロ次元量子ドット(QD)などの他のナノスケール構造とのMBSのハイブリッド化です[ 16、17]。低温では、QDのエネルギーレベルがリードのフェルミエネルギーに整列しているときの最大コンダクタンスの半分が、MBSのペアの形成の明確な証拠として理論的に予測されました[18]。この結果は、QDエネルギーレベルの調整によって変更されずに完了し[19]、InAs-Alナノワイヤに結合されたQDでの実験で正常に観察されました[20]。最近、QD構造に基づく光学スキームも理論的に提案され、光ポンププローブ技術の助けを借りてMBSを検出しました。 [21、22]リング型またはT型のQDベースのシステムでは、量子干渉現象はMBS [23–25]の影響を大きく受け、たとえば、ファノ効果[26–28]。
最近、電気エネルギーと熱エネルギーの間の変換に焦点を当てた、熱電効果によるMBSの検出に関するいくつかの研究もあります。この古い研究トピックは、熱電性能が明らかに改善されているメゾスコピックデバイスとナノ構造の成長と製造の急速な進歩により、新たな注目を集めています[29、30]。最近、GaAs / AlGaAs界面の二次元電子ガスなどで定義された量子ドットに基づく高効率環境発電機が報告されています[31、32]。それらの熱電効果の強化は、境界散乱による熱伝導率の大幅な低下と、これらの低次元システムに特有の電気輸送特性の最適化に起因する可能性があります[30–32]。熱電能(ゼーベック係数)は、熱電効果の中心的な量です。これは、自由な電子キャリアを備えた固体材料に適用される温度勾配に応答する開回路電圧の強さです。 Hou etal。マヨラナエッジ状態をホストするQDと超伝導体の間の熱電能は、モットの公式を満たし、Landauer-Büttiker形式を使用しても一般的に消失しないと理論的に予測されました[33]。このような性質に基づいて、微分コンダクタンスと熱出力を測定することにより、マヨラナエッジ状態の温度を推測することができます。 Leijnseは、調整可能なエネルギー準位を持つQDとMBSの間の結合が粒子と正孔の対称性を壊し、熱電能の変化がマヨラナ状態の存在を証明する新しい方法を提供することを理論的に示しました[34]。このようなセットアップの熱電特性は、超伝導体の温度を検出し、MBSの散逸減衰に関する情報を抽出するためにも使用できます[34]。 2つの電極に結合されたQDを持つ構造において、Lópezetal。は、MBS間の直接混成を変更することにより、熱電能がその符号を変更することを示しました。これは、MBSの存在の良い証拠です[35]。その後、熱電能の符号の変化は、2つの[36]または3つの[37]電極を備えたQDのシステムでも見られました。さらに、ショットノイズと熱電量の関係が、電荷に中立なMBSを検出するための純粋に電気的な方法を提供する可能性があることが実証されました[38、39]。
本論文では、MBSと電極に結合されたQDで構成されるハイブリッドシステム(図1を参照)を提案し、熱電能の特性を研究します。私たちが検討したナノシステムでは、以前の研究[18、22–24、34–39]で無視されていた、ドット内の強いクーロン相互作用が考慮されています。さらに、MBSのキラル性により、QDスピンの1つのスピン成分のみがMBSに結合していると考えられます[40]。ドット-MBS結合強度、MBS間の直接混成、およびシステム温度を変更することにより、熱出力の符号を効果的に反転できることがわかります。結果として得られる大きな100%スピン偏極および純粋なスピン熱電能は、閉回路における対応する100%スピン偏極および純粋なスピン電流であり、スピントロニクスに役立ちます。 2つのMBSの両方をQDに結合すると、熱出力の大きさがさらに向上しますが、MBSの1つだけがドットに結合されている場合の本質的な結果は変わりません。トポロジカル超伝導ナノワイヤと組み合わせたQDを介したMBSの現在高度な量子輸送測定に基づいて、私たちの提案は将来実験的にテストできると信じています。さらに、この作業での提案と調査結果は、QDでのMBSの形成を検出するための優れた方法を提供する可能性があります。
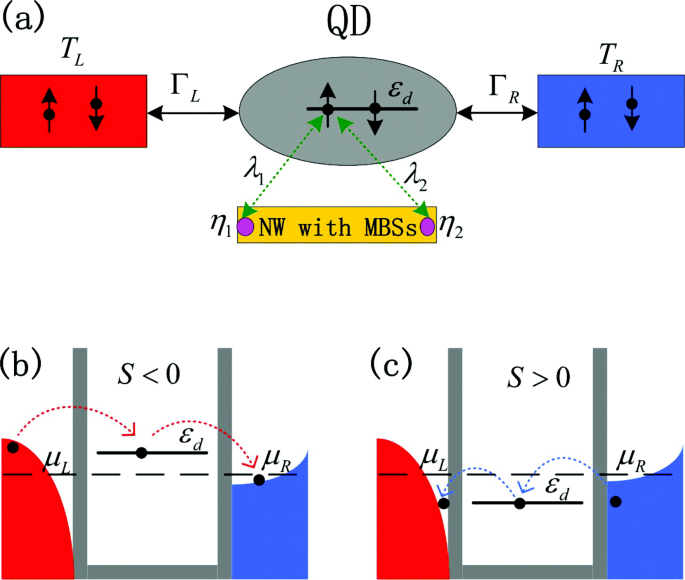
モデルの概略図(オンラインカラー)。 a ゲート調整可能なエネルギーレベルεのQDで構成されるシミュレーション構造の概略図 d これは、スピンアップ電子またはスピンダウン電子のいずれかによって占有される可能性があります。 QDは、結合強度Γで異なる温度に保持された左右のリード線に接続されます L / R 。 MBS η 1/2 半導体ナノワイヤの端に形成され、λの強度を持つマヨラナフェルミ粒子のキラル性によりQDのスピンアップ電子に結合します。 1 およびλ 2 、 それぞれ。スピンアップ電子のエネルギー状態はMBS-QD結合によって変化し、次に熱電能の強度と符号が変化します S 影響を受けます。現在のモデルでは、左側のリード線の温度 T を想定しています。 L 正しいものよりも高い T R 、そして、右のリードよりも左のリードの化学ポテンシャルの上(下)で励起される電子(空の状態)が多くなります。 b 、 c 電子トンネリングプロセスと、MBS-QD結合がない場合の結果として生じる熱電能。 b で 、QDエネルギーレベルε d リードの化学ポテンシャルを上回っていますμ L / R =μ 、そして、占有状態からの電子ε d > μ 左側の高温のリードはドット状態εをトンネリングします d 右の冷たいリード線で空の状態になり、結果として負のサーモポッパー S <0。 c で 、ε d <μ 、そして、それに応じて熱電能の符号が逆になります
モデルとメソッド
MBSおよび左右の通常の金属電極に結合されたQDの有効なハミルトニアンは次の形式を取ります[34、35]:
$$ \ begin {array} {@ {} rcl @ {}} H&=\ sum_ {k \ beta \ sigma} \ varepsilon_ {k \ beta} c_ {k \ beta \ sigma} ^ {\ dag} c_ { k \ beta \ sigma} + \ sum _ {\ sigma} \ varepsilon_ {d} d _ {\ sigma} ^ {\ dag} d _ {\ sigma} + Ud _ {\ uparrow} ^ {\ dag} d _ {\ uparrow} d_ {\ downarrow} ^ {\ dag} d _ {\ downarrow} \\&+ \ sum_ {k \ beta \ sigma}(V_ {k \ beta} c_ {k \ beta \ sigma} ^ {\ dag} d _ {\ sigma} + Hc)+ H _ {\ text {MBSs}}、\ end {array} $$(1)ここで、\(c_ {k \ beta \ sigma} ^ {\ dag}(c_ {k \ beta \ sigma})\)は、運動量の電子を作成(消滅)します k 、エネルギーε k β (通常の金属電極ではスピンへの依存性は無視されます)、スピンσ =↑ 、↓ 電極内β = L 、 R 。 QDの場合、\(d _ {\ sigma} ^ {\ dag}(d _ {\ sigma})\)は、ゲート電圧の調整可能なエネルギーレベルεを持つ電子の生成(消滅)演算子です。 d 、スピン-σ 、およびドット内クーロン相互作用 U 。 QDとリード間の結合強度は V で表されます。 k β 。最後の用語 H MBS 式で。 (1)は、半導体ナノワイヤの両端にあるゼロエネルギーMBSと、QDへの結合を表します[18]:
$$ \ begin {array} {@ {} rcl @ {}} {} H _ {\ text {MBSs}} =i \ delta_ {M} \ eta_ {1} \ eta_ {2} + \ lambda_ {1}( d _ {\ uparrow} -d _ {\ uparrow} ^ {\ dag})\ eta_ {1} + i \ lambda_ {2}(d _ {\ uparrow} + d _ {\ uparrow} ^ {\ dag})\ eta_ { 2}、\ end {array} $$(2)ここでδ M は、2つのMBS間のオーバーラップ振幅であり、演算子は\(\ eta _ {j} =\ eta _ {j} ^ {\ dag}(j =1,2)\)と{η> i 、η j } =δ i 、 j 。 MBSとスピン間のホッピング振幅-↑ QD内の電子はλによって説明されます j 。 ηと書くと便利です j 通常のフェルミ粒子演算子の観点から f as [18] \(\ eta _ {1} =(f ^ {\ dag} + f)/ \ sqrt {2} \)および\(\ eta _ {2} =i(f ^ {\ dag}- f)/ \ sqrt {2} \)、次に H MBS 次のように書き直されます:
$$ \ begin {array} {* {20} l} H _ {\ text {MBSs}}&=\ delta_ {M} \ left(f ^ {\ dag} f- \ frac {1} {2} \ right )+ \ frac {\ lambda_ {1}} {\ sqrt {2}} \ left(d _ {\ uparrow} -d _ {\ uparrow} ^ {\ dag} \ right)\ left(f ^ {\ dag} + f \ right)\\&-\ frac {\ lambda_ {2}} {\ sqrt {2}}(d _ {\ uparrow} + d _ {\ uparrow} ^ {\ dag})\ left(f ^ {\ dag }-怖じけ)。 \ end {array} $$(3)線形応答レジームのシステム、つまり、無限に小さいバイアス電圧Δの下でシステムを検討します。 V と温度差Δ T 左右のリード線の間で、各スピン成分の電流と熱電流は次のように取得されます。
$$ \ begin {array} {* {20} l}&I_ {e、\ sigma} =-e ^ {2} L_ {0、\ sigma} \ Delta V + \ frac {e} {T} L_ {1、 \ sigma} \ Delta T、\ end {array} $$(4)$$ \ begin {array} {* {20} l}&I_ {h、\ sigma} =eI_ {1、\ sigma} \ Delta V- \ frac {1} {T} L_ {2、\ sigma} \ Delta T、\ end {array} $$(5)ここで e は電子の電荷であり、 T システム平衡温度、および
$$ \ begin {array} {@ {} rcl @ {}} L_ {n、\ sigma} =\ frac {1} {\ hbar} \ int(\ varepsilon- \ mu)^ {n} \ left [- \ frac {\ partial f(\ varepsilon、\ mu)} {\ partial \ varepsilon} \ right] T _ {\ sigma}(\ varepsilon)\ frac {d \ varepsilon} {2 \ pi}、\ end {array} $$(6)ここで、\(\ hbar \)は縮小プランク定数です。リードの化学ポテンシャルを設定しますμ エネルギーゼロ点として=0。フェルミ分布関数は f で与えられます。 (ε 、μ )=1 / {1 + exp [(ε − μ )/ k B T ]} with k B ボルツマン定数です。透過係数 T σ (ε )は、遅延グリーン関数を使用して次のように計算されます。
$$ \ begin {array} {@ {} rcl @ {}} T _ {\ sigma}(\ varepsilon)=\ frac {\ Gamma_ {L} \ Gamma_ {R}} {\ Gamma_ {L} + \ Gamma_ { R}} [-2 \ text {Im} G _ {\ sigma} ^ {r}(\ varepsilon)]、\ end {array} $$(7)ここで、\(\ Gamma _ {L(R)} =2 \ pi \ sum _ {k} | V_ {kL(R)} | ^ {2} \ delta [\ varepsilon- \ varepsilon _ {kL(R)} ] \)は線幅関数です。グリーン関数を取得するために、標準の運動方程式手法を適用します。高階グリーン関数は、参考文献のスキーム2に従うことによって切り捨てられます。 [39]、すなわち、反対のスピンの電子の同時トンネリングを無視します。いくつかの簡単な計算の後、スピンアップ遅延グリーン関数は次の式で与えられます。
$$ {\ begin {aligned} G _ {\ uparrow} ^ {r}(\ varepsilon)=\ frac {\ varepsilon _ {-}-\ Sigma ^ {M} _ {1} -U \ left \ {1-ここで、MBSによって誘発される自己エネルギー
$$ \ Sigma ^ {M} _ {0} =B_ {1} + \ left(\ lambda_ {1} ^ {2}-\ lambda_ {2} ^ {2} \ right)^ {2} B \ tilde {B}、$$(9)および
$$ \ Sigma ^ {M} _ {1} =B_ {1} + \ left(\ lambda_ {1} ^ {2}-\ lambda_ {2} ^ {2} \ right)^ {2} B \ tilde {B} _ {U}、$$(10)と
$$ \ begin {array} {* {20} l}&B =\ frac {\ varepsilon} {\ varepsilon ^ {2}-\ delta_ {M} ^ {2}}、\ end {array} $$(11 )$$ \ begin {array} {* {20} l}&B_ {1} =\ frac {1} {2} \ left(\ frac {\ lambda_ {1} ^ {2}-\ lambda_ {2} ^ {2}} {\ varepsilon- \ delta_ {M}} + \ frac {\ lambda_ {1} ^ {2} + \ lambda_ {2} ^ {2}} {\ varepsilon + \ delta_ {M}} \ right) 、\ end {array} $$(12)$$ \ begin {array} {* {20} l}&\ tilde {B} =\ frac {B} {\ varepsilon _ {+} + B_ {2}}、 \ end {array} $$(13)$$ \ begin {array} {* {20} l}&\ tilde {B} _ {U} =\ frac {B} {\ varepsilon _ {+} + U-B_ {2}}、\ end {array} $$(14)$$ B_ {2} =\ frac {1} {2} \ left(\ frac {\ lambda_ {1} ^ {2}-\ lambda_ {2} ^ {2}} {\ varepsilon + \ delta_ {M}} + \ frac {\ lambda_ {1} ^ {2} + \ lambda_ {2} ^ {2}} {\ varepsilon- \ delta_ {M}} \ right)、$$(15)
およびε ± =ε ±ε d + i (Γ L + Γ R )/ 2。ドット-MBSハイブリダイゼーションがない場合(λ 1 =λ 2 =0)、\(\ Sigma ^ {M} _ {0,1} =0 \)があり、\(G _ {\ uparrow} ^ {r}(\ varepsilon)\)はrefの値を回復します。 [39]。これは、 n を変更することによるスピンダウン遅延グリーン関数でもあります。 ↓ n に ↑ 。職業数は、以下から一貫して計算されます:
$$ \ begin {array} {@ {} rcl @ {}} n _ {\ sigma} =\ int \ frac {d \ varepsilon} {2 \ pi} \ frac {\ Gamma_ {L} f_ {L}(\ varepsilon)+ \ Gamma_ {R} f_ {R}(\ varepsilon)} {\ Gamma_ {L} + \ Gamma_ {R}} [-2 \ text {Im} G _ {\ sigma} ^ {r}(\ varepsilon )]、\ end {array} $$(16)ここで f L / R (ε )は、左/右電極のフェルミ分布関数です。
グリーン関数から伝達関数が得られると、各スピン成分の電気コンダクタンスと熱電能(ゼーベック係数)は G で与えられます。 σ = e 2 L 0、σ および S σ =− L 1、σ /( e T L 0、σ )、それぞれ。
結果と考察
以下では、QDと電極間の対称結合を想定し、Γを設定します。 =2 Γ L =2 Γ R エネルギー単位として=1。ドット内クーロン相互作用は U として固定されています =10 Γ 。まず、ハイブリダイゼーション強度が異なるMBS-1のみに結合したQDの場合を検討しますλ 1 図2では、λを設定します。 2 =0。 λの場合 1 =0の場合、図2aの各スピン成分のコンダクタンスは、それぞれεに位置する2つのピークを生成します。 d =− μ および− μ − U 。ここで、QDにはMBSによって引き起こされるスピン偏極がなく、2つのスピン成分のコンダクタンスは互いに等しいことに注意してください( G ↑ = G ↓ )、 によると。 MBSとQD間のハイブリダイゼーションをオンにする(λ 1 ≠0)、 G の大きさ ↑ 図2aに示すように、は単調に抑制されます。これは、以前の結果と一致しています[18、34、35]。 G の値 ↓ ただし、職業番号 n でもほとんど変わりません。 ↓ λによって変更されます 1 ドット内クーロン相互作用の存在によるものです(これは図には示されていません)。一方、 G のピークの位置と幅 ↑ λの値によってわずかに変更されます 1 ドット-マヨラナ結合によるレベル繰り込みによる[18、34、35]。総コンダクタンスの構成 G = G ↑ + G ↓ 図2cは、 G の図に似ています。 ↑ 。
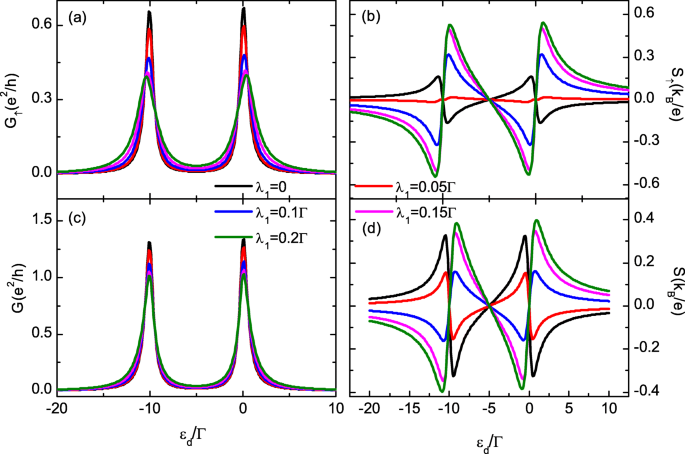
さまざまなドット-マヨラナ結合強度のスピン依存コンダクタンスと熱出力(オンラインカラー)。 a のスピンアップと総コンダクタンス 、 c および b の熱電能 、 d 詩のドットレベル。スピンダウンコンダクタンスと熱出力は、ドット-マヨラナ結合強度λによってほとんど変化しません。 1 、およびそれらは a の黒い実線と重なります および c 、 それぞれ。その他のパラメータは温度 T =0.025 Γ 、Δ M =0、 U =10 Γ 、およびλ 2 =0
サーモパワー S ↑ 図2bは、典型的な鋸歯状の構成を示しており、εに個別に3つのゼロ点があります。 d =μ 、− U / 2、およびμ − U [41、42]。 2つの共振状態(ε)のそれぞれで反対の符号を持つ一対の鋭いピークを発生させます d =μ 、μ − U )そしてεのたびに符号を変更します d 各ゼロ点を渡します。ドット-MBSハイブリダイゼーションがない場合(λ 1 =0)図2bの黒い実線で示されているように、 S ↑ εの場合は正(負)です d 主なキャリアは電子(正孔)であるため、はゼロ点より下(上)にあります。 λの増加に伴い 1 、スピンダウンサーモパワー S ↓ は変更されず、 S の絶対値 ↑ 最初に抑制され、次に強化されます。十分に大きいλの場合 1 、 S ↑ 図2bに示すように符号を変更します。さらに増加したλ 1 、 S の絶対値 ↑ S のそれを超える ↓ および総熱出力 S = S ↑ + S ↓ また、その符号を変更します。このような現象は、スピンレスモデルでも以前に発見されています[35–37]。実際、MBSのないQDベースのデバイスの熱出力の符号変化は、システム平衡温度[29]、電極の磁気モーメント[43]、クーロン相互作用[43、44]、結合などのいくつかの原因に起因していました。 QD間の強度、印加磁場、量子干渉効果、または複数ドットのものを貫通する磁束[45、46]。上記のメカニズムは現在の場合とはまったく異なり、QDとMBSの間の混成を変更することによる熱出力の符号の変更は、MBSの検出に役立ちます[35–37]。
図3a、bは、総コンダクタンス G を示しています。 とthemopower S ドットレベルによって異なりますε d 温度のさまざまな値 T 。 G のピーク値 図3aに示すように、最初に強化され、次に温度を上げることによって抑制されます。ただし、図3bの熱電能の大きさは、化学ポテンシャルの上(下)で励起される電子(正孔)が多いため、主に温度を上げることによって強化されます。さらに、 S T の場合の符号を変更します 図3bのピンクと緑の線で示されているように=0.1と0.2。これは、MBSのないQDベースの構造での熱電効果の場合と同様です。 T の場合 =0.2 Γ 、 S のピーク値 2 k に達する可能性があります B / e 、これは T よりも1桁大きい =0.001。実際、温度を上げることで熱電能の大きさをさらに高めることができることを確認しました。ただし、本稿では、 S の符号変更に焦点を当てます。 比較的低温で、これは通常、実験で形成されたMBSの場合です。図3c、dは、固定された T でのナノワイヤの両端にある2つのMBSの直接混成の異なる値のコンダクタンスと熱出力を示しています。 =0.025 Γ 。図3cのコンダクタンスのピーク値は、δを増加させることによって単調に増強されます。 M 、これはLópezらによって発見された結果と一致しています。 [35]。図3dの熱出力は、0.03 Γの符号を変更します。 <δ M <0.05 Γ 、温度 T よりも大きい =0.025 Γ 。参考文献で。 [32]、彼らは熱電能が約δでその符号を変えることを発見しました M ≈ k B T スピンレスモデルで。本稿では、 S の符号変更 比較的大きなδで発生します M MBSは1つのスピン方向の電子にのみ結合しているためです。さらに、サーモパワーのピーク値は、δを増やすことによっても高めることができます。 M 。
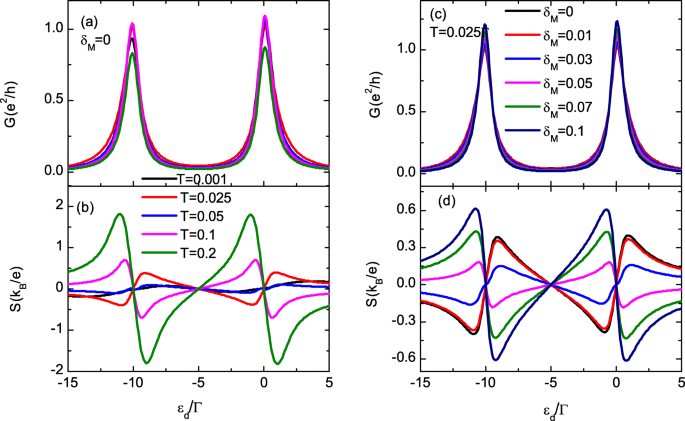
コンダクタンスとサーモパワー(オンラインカラー)。総コンダクタンスのカウンタープロット G およびサーモパワー S εの関数として d およびΔ M a で 、 b 、温度 T c で 、 d 、 それぞれ。 λの値 1 0.2 Γとして固定されています 。 a の温度 、 c は0.025 Γです 、および c 、 d Δ M =0。その他のパラメータは図2と同じです
λの関数としてスピン分解熱出力を個別に示します 1 およびδ M 図4のスピンアップサーモパワー S ↑ 図4aでは、最初に増加して最大に達し、次にλの増加とともに減少します。 1 。十分に大きいλ 1 、安定した値のままです。スピンダウンサーモパワーの値 S ↓ λによって変更されません 1 予想通り。 S の動作 ↑ および S ↓ 2つの興味深い結果をもたらします。1つは S の場合の100%スピン偏極熱出力です。 ↑ =0、ただし S ↓ 電子スピンのフィルタリングに使用できる有限値を持っています。もう1つは、有限の純粋なスピン熱電能 S です。 s = S ↑ − S ↓ ゼロチャージサーモパワー S c = S ↑ + S ↓ =0 S のときに発生しました ↑ =− S ↓ 図4bの点で示されているように。閉回路では、100%のスピン偏極と純粋なスピン熱出力は、個別に対応する電流であり、スピントロニクスデバイスでは仮想的です。同様の結果が図4b、dに見られます。ここで、 S ↑ δを変更することにより符号が変更されます M 、一方、 S ↓ 変更されません。現在の100%スピン偏極した純粋なスピン熱電能は、QDに磁場や磁性材料がない場合に出現することを強調します。
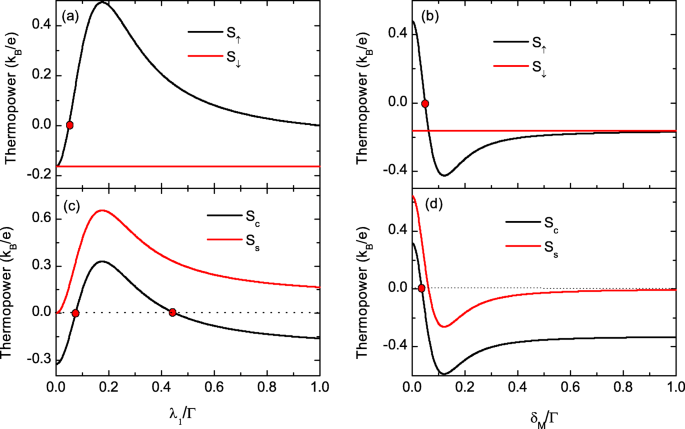
ドット-マヨラナ結合強度と直接重なりによって変化する熱出力。 λの関数としての熱出力 1 a で 、 b Δ M =0、およびΔ M c で 、 d λ 1 =0.2 Γ 、 それぞれ。その他のパラメータは図2と同じです
図5では、ナノワイヤの両端にある両方のMBSが、ワイヤとドットがδで十分に接近しているときにQDに結合されている場合を示しています。 M =0。図5aは、総コンダクタンス G を示しています。 λが存在する場合でもダブルピーク構成を維持します 2 。 λを大きくすると、ピークの高さが抑制されます。 2 。 S の線形 λの値によっても変更されません 2 図5bに示すように。 S のピーク値 サーモパワーはコンダクタンスに反比例するため、大幅に向上します。 λの場合 2 〜0.2 Γ 、熱電能の大きさは2 k に達する可能性があります B / e 。さらに、 S λの値を調整しても符号は変わりません 2 。図6は、εの関数としての総熱出力を示しています。 d MBS間の直接ハイブリダイゼーションの値が異なる場合δ M λを修正する 1 =λ 2 =0.2 Γ 。 δを調整することにより、大きさと符号の両方を効果的に変更できることを示しています。 M 、これは、MBSの1つだけがQDに結合されている場合と同様です。最後に、現在のデバイスの実験的実現について簡単に説明します。 MBSをホストするナノワイヤは、数ナノメートルのエピタキシャルAl層を用いた分子線エピタキシーによって成長させたInAsを使用して製造できます[47]。ワイヤ軸に沿って2Tを超える臨界磁場を印加することにより、このような種類のナノワイヤに硬い超伝導ギャップを誘導できることが実験的に証明されています[47、48]。 QDは、Alシェルのエッジでの状態密度勾配のためにワイヤの端の裸のInAsセグメントに形成されます[20、47、48]。
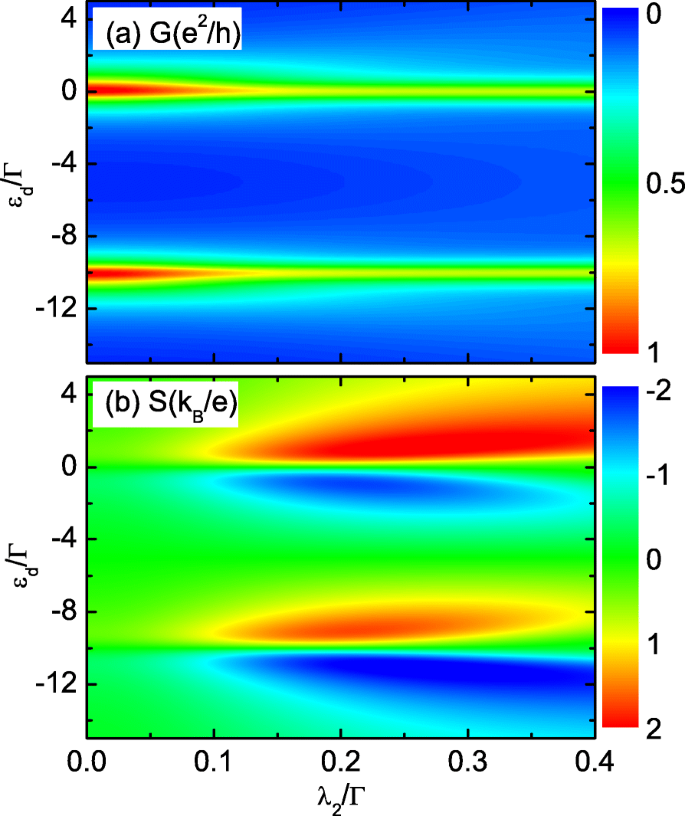
他のドット-マヨラナ結合が熱電能に与える影響(オンラインカラー)。 λの影響 2 総コンダクタンスについて( a )およびサーモパワー( b )λを使用 1 =0.2 Γ 、δ M =0。その他のパラメータは図2と同じです
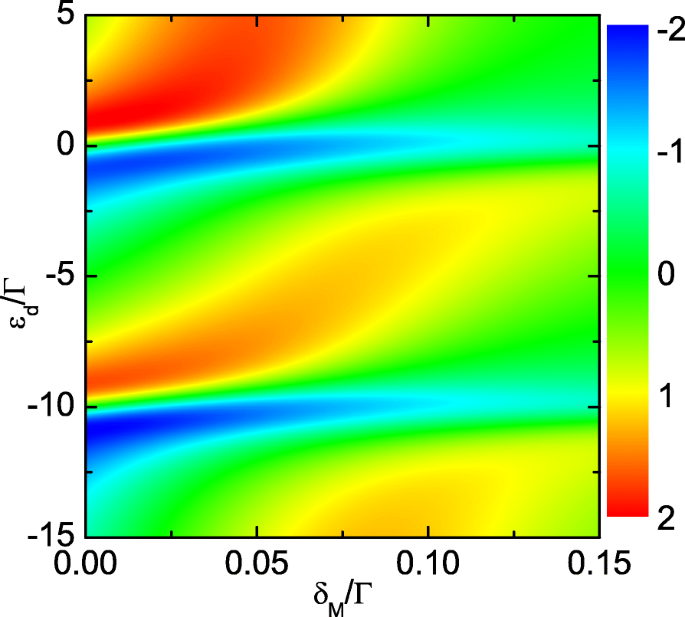
サーモパワーのカウンタープロット(オンラインカラー)。 εの関数としての熱出力のカウンタープロット d およびλ 2 λの場合 1 =0.2 Γ 。その他のパラメータは図2と同じです
結論
結論として、我々は、クーロン相互作用で左右の通常の金属電極に接続された量子ドットの電気コンダクタンスと熱電能の特性を研究しました。ドットは、半導体ナノワイヤで形成されたMBSにも結合されます。スピンアップ電子とスピンダウン電子はクーロン反発を介して相互作用しますが、MBSはそれが結合するだけのスピン成分のコンダクタンスと熱出力に影響を与えることがわかります。熱電能の符号は、ドット-MBSの混成強度、MBS間の方向混成、およびシステム温度を調整することで変更できます。非磁性QD構造では、100%スピン偏極または純粋なスピン熱出力のいずれかの大きな値を得ることができます。ドットと2つのMBSの両方の間の結合は、熱電能の大きさのみを変更でき、その符号は変更できません。私たちの結果は、熱電技術を介してMBSの存在を検出するのに役立つ可能性があります。
データと資料の可用性
この記事の結論を裏付けるデータセットは、記事に含まれています。
略語
- QD:
-
量子ドット
- MBS:
-
マヨラナ束縛状態
ナノマテリアル
- 量子輸送は弾道的になります
- 異なる電荷状態のイメージング分子
- 平面ナノホールスラブを使用した連続体の二重束縛状態によって誘発される高品質係数デュアルバンドファノ共鳴
- 効率的な光触媒水素生成のためのS、N共ドープグラフェン量子ドット/ TiO2複合材料
- マイクロピラーのInAs二重層量子ドットに基づく1.3μmの明るい単一光子源
- 自己組織化InAs / InGaAs量子ドット超格子における空間的に局在化した励起子の検出:光起電効率を改善する方法
- 変成InAs / InGaAs / GaAs量子ドットヘテロ構造の光起電力における双極効果:光感受性デバイスの特性評価と設計ソリューション
- コア/シェルCdSe / ZnS量子ドットフィルムの光励起発光に対する可逆的電気化学的制御
- ナノワイヤ/量子ドットハイブリッドナノ構造アレイ太陽電池の光起電力性能
- 1.3μm量子ドットレーザーの調製のためのInAs / GaAs量子ドットのバイモーダルサイズの排除
- MBiおよびMSb(M:Ti、Zr、およびHf)ハニカムにおける量子異常ホール効果の予測



