中赤外領域のシリコン回折格子上でのグラフェンによる高効率プラズモニック第3高調波発生

はじめに

調和生成は非線形光学プロセスであり、同じ周波数のN個の光子ω 非線形材料との相互作用が組み合わされて、周波数Nωの新しいフォトンが生成されます。 。コヒーレント光源を短波長に拡張する手段として、第3高調波発生（THG）が大きな研究関心を集めています。従来、高効率の高調波発生はエキゾチックな結晶で実現されていましたが、これは高密度フォトニック集積を損ないます[1]。シリコンは、高度に統合されたフォトニック回路で光信号を送信するための光情報キャリアとして成熟した材料の選択肢になりました。誘導ラマン散乱[2]やTHG [3,4,5]などの非線形光学効果は、シリコンフォトニクスの機能を広げる大きな可能性を秘めています。ただし、シリコンを使用した効率的な発光は、その間接バンドギャップのために依然として困難な問題です。 THGなどの非線形光学相互作用を使用することは、シリコンフォトニクスにコヒーレント光を提供するためのかなり有望なアプローチのようです。一般に、光導波路のTHG変換効率（CE）は、基本波モードと第3高調波モードの間の位相整合を使用することによって向上させることができます。この方法では通常、複雑な構成が必要であり、実際の状況では実装が困難です。 THG CEを強化するための効果的で堅牢な方法は、非線形材料内の光強度を増加させることによって作成できます。これにより、位相整合条件に対する厳しい要求を緩和する機会が得られます。これは最近、超高品質係数の低速光シリコンフォトニック結晶[3,4,5]、小モーダルボリュームのシリカマイクロロッド[6]、および表面プラズモン[7,8,9,10]を使用して実現されました。シリコンフォトニック結晶がTHGCEを〜10 ^-7 の大きさに改善したことが報告されています。 c / 40の群速度の低下による[4]。ごく最近、表面プラズモンがTHGCEを10 ^-5 のオーダーまで増加させることができることが証明されました。 タイトな電界増強による[7]。

近年、シリコンフォトニクスの動作波長は、化学的および生物学的センシングなどの多くの潜在的なアプリケーションにより、中赤外線および遠赤外線（IR）領域にまで拡大しています[11]。プラズモニック導波路の伝搬損失は長波長で劇的に減少し、またそのような導波路のモード断面はサブ波長であるため、中赤外および遠赤外領域でのプラズモニクスの使用は魅力的です。 THG変換[7、8、9、10、12、13]。最近の研究により、グラフェンは非線形効果を高める優れた非線形光学材料として機能し、4光波混合[14、15]、THG [16、17、18]、全光スイッチング[19]、三次非線形光学感受率が大きいため、光双安定性[20、21]。特に、グラフェンの大きな3次非線形光学感受率のおかげで、観測された光双安定性のしきい値を大幅に下げることができます[20、21]。さらに興味深いことに、金属のプラズモンモードとは対照的に、グラフェンプラズモン（GP）は、波数ベクトルが大幅に大きく、光の閉じ込めがはるかに高いため、THGのCEをさらに強化できることがわかります[13]。ただし、基本周波数（FF）GPと放射波の間の直接結合は、それらの運動量の不一致のために妨げられ、このスキームの実装は実際には困難な問題になります。研究者が結合の問題に対処するためにグレーティングのガイドモード共振を採用したのはこのためです[12、18、20]。参考文献で提案されたスキーム。 [18]は、FF GPを直接励起し、テラヘルツ領域の第3高調波周波数（THF）自由空間波のCEを強化するように意図的に設計されています。

この記事では、グラフェンシート上のFF GPを効率的に励起するために、グレーティングのガイドモード共振も使用しました。参考文献の構成とは異なります。 [18] GPを使用してテラヘルツ領域のTHF自由空間波のCEを強化する場合、ここでは、GPを使用してシリコンチップ上に赤外線周波数でTHFGPを生成します。グラフェンの大きな3次非線形感受性と組み合わせたFFGPの巨大な電界強度により、中IRおよび遠IR領域のグラフェンシート上のTHFGPのCEが著しく向上します。グラフェン表面のTHFGPのCEを改善するために準位相整合条件を使用することに関する以前の研究に注目します[13]。ただし、ここでは強調しますが、参考文献ではFFとTHFGPの間の高いCEが達成可能です。 [13]、放射波とGPの間の直接結合が欠落しています。対照的に、提示されたスキームは、空間FF波と直接結合できるだけでなく、THF GPを非常に効率的に生成できるため、シリコンフォトニックプラットフォームでの統合に適した提案になります。さらに、実証されたプラズモン周波数変換器は、小さな入射電力を必要とする一方で、コンパクトで高いCEという利点があります[22、23]。

メソッド

グラフェンの表面伝導率は、化学ポテンシャル（フェルミエネルギーとも呼ばれる）μを仮定して、広く使用されている久保公式によって推定できます。 _c 。赤外線およびテラヘルツ周波数では、| μ _c | ≫ k _B T （ k _B はボルツマン定数であり、 T は温度です）、グラフェンの表面抵抗率は次のように概算できます

ここで e は電子の電荷、ℏは減少したプランク定数、ωです。 はラジアン周波数であり、τ 損失メカニズムを表す運動量緩和時間です。私たちの研究では、動作温度は T であると想定されています =300K。個々のグラフェンシートを相互作用しない単分子層と見なすことにより、数層のグラフェンの光伝導率はnσになります。 _g [24]、ここで n はグラフェン層の数です（ n <6）。グラフェンを異方性材料としてモデル化し、有効面内誘電率は[25、26]と書くことができます。

ここでη ₀ （=377Ω）は空気のインピーダンス、 k ₀ は空中の波数ベクトルであり、 d _g は n の合計の厚さです -層グラフェンシート。グラフェンの面外誘電率、ε _y 、フェルミ準位に関係なく、2.5で一定に保たれます[27、28]。

結果と考察

シリコン格子を使用したFFGPの励起

まず、図1に示すように、誘電体格子（GSSDG）によって維持されたグラフェンシート上でのFFGPの励起とTHFGPの生成を検討します。グラフェンの面積が数百倍になるという実際の状況を考慮します。グレーティングセクションでは、グラフェンシートはグレーティングの上部で平らであり、グレーティングに適合していないと想定されます。グラフェンシートが平坦であると想定される格子によって維持されるグラフェンシートによってサポートされるGPに関するいくつかの調査研究に注目しました[12、13]。特に、実験結果は、モデリングでグラフェンシートが平坦であると仮定されているシミュレーション結果とよく一致していることがわかります[12]。 GSSDGは、 x に沿って無限であると見なされます z に沿った方向と周期 方向。グラフェンシート下のシリコン格子層の厚さは2μmと想定されています。この場合、グレーティングの下のシリコン基板はエアグラフェングレーティングモデルのGPの電界分布に影響を与えないため、グレーティング層はモデリングで無限に厚いと見なすことができます。この構成でサポートされるGPの分散関係は、[29]として表すことができます。

ここで、β z-に沿ったGPの伝播定数です 軸、ε ₀ は空気中の誘電率であり、ε _{r 1} （=1）およびε _{r 2} は、それぞれグラフェン層の上下の誘電体の誘電率です。回折格子の周期は空気中の光の波長よりもはるかに小さいため、シリコン回折格子は、同等の誘電率を持つ有効な媒体として近似的にモデル化できます[30]。

ここで、ε _シリコン （=11.9）は、赤外線およびテラヘルツ周波数[31]、および f でのシリコンの誘電率です。 （= w / p ）はシリコンの充填率（ f この作業では0.5に固定されています。

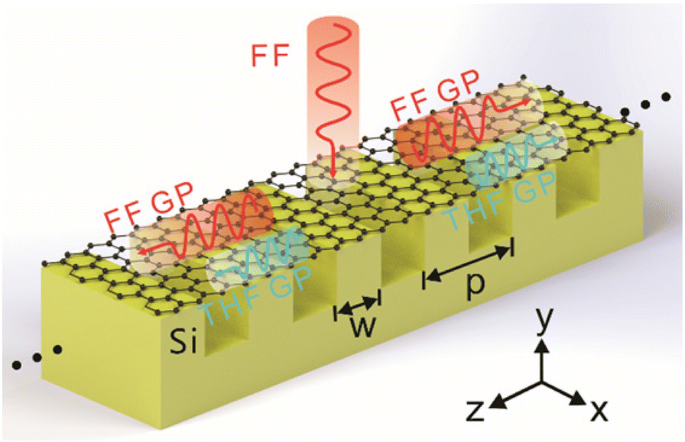
THG波長変換器としてのGSSDGのスキーム。 FF GP（赤い曲線）は、FFの法線入射x偏波平面波で励起され、グラフェンシートの下にあるシリコングレーティングによってTHF GP（青い曲線）を生成します。グレーティングの周期は p です。 、および w シリコンの幅を示します

さまざまなパラメータ（τ）に対するGSSDG上のGPの分散関係 、μ _c 、および d _g ）を図2に示します。全体の作業では、数値モデリングを行うために、Lumerical FDTD Solutionの商用ソフトウェアを使用した2次元有限差分時間領域（FDTD）が実行されます。この部分のシミュレーションでは、 y で完全一致層境界と周期境界が使用されます。 および z 構造全体が x に沿って無限であると想定されている間、それぞれ方向。 方向。 y に沿った0.1nmのメッシュサイズ 方向と z に沿った10nm 方向はグラフェンを表すために使用されますが、 y に沿って最大値が20nmの不均一なメッシュ z に沿った方向と10nmの均一メッシュ グラフェンシート以外の領域では方向を採用しています。図2a、d、gから、考慮した波長範囲内で、GPの波数ベクトルは空気の波数ベクトルの数十倍であることがわかります。これは、GPの光場がグラフェン表面。ただし、GPと放射波の間の位相の不一致により、GP間の直接結合が妨げられます。図1に示すグラフェンシートの下のシリコン回折格子は、波数ベクトルの差を克服するための追加の運動量を提供できるため、FFGPは平面波の入射で効率的に励起できます。グレーティング周期、 p 、次のように位相整合方程式を満たす必要があります

ここで、β _FF z に沿ったFFGPの伝播定数です。 -軸、 j は回折次数であり、θ は入射角です。 λの有効波長のFFGPを励起する _FF 基本回折次数 j 法線入射θの条件下で=1 =0、次の式が満たされる必要があります

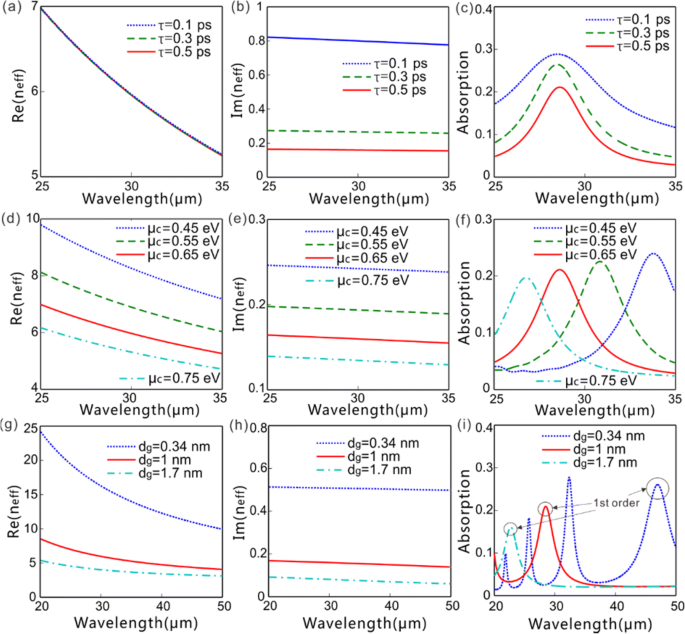
実際の[Re（ n _eff ）]および虚数[Im（ n _eff ）]実効屈折率の一部、およびμの値が異なる場合の吸収と波長の関係 _c 、τ 、および d _g 。 a – c Re（ n _eff ）、Im（ n _eff ）、および吸収対波長（τ =0.1、0.3、および0.5 ps、μに関連付けられています =0.14、0.42、0.69 m ² V ^-1 s ^-1 、それぞれ）μ _c =0.65eVおよび d _g =1nm。 d – f Re（ n _eff ）、Im（ n _eff ）、および吸収対波長（μ _c =0.45、0.55、0.65、および0.75 eV）、τ =0.5psおよび d _g =1nm。 g – i Re（ n _eff ）、Im（ n _eff ）、および吸収対波長[ d _g =0.34 nm（ n =1）、1 nm（ n =3）、および1.7 nm（ n =5）] μ _c =0.65eVおよびτ =0.5ps。すべての場合において、グレーティング周期は p に固定されています。 =4μm

図2は、実際の[Re（ n _eff ）]および虚数[Im（ n _eff ）] τの値が異なる光波長の実効屈折率と吸収の一部 、μ _c 、および d _g 。グラフェンのパラメータが、格子周期が4μmに固定されているFFの法線入射x偏光平面波の照明下で励起されたFFGPにどのように影響するかを明らかに説明しています。両方の実際の[Re（ n _eff ）]および虚数部[Im（ n _eff ）] FF GPの有効屈折率は、考慮される波長範囲内の光波長の増加とともに減少します（図2a、b、d、e、g、h）。これは、光の波長が短いほど、GPがグラフェンシートの周囲により強く閉じ込められ、伝搬定数が大きくなり、伝搬損失が大きくなることを意味します。吸収は波長に非常に敏感であり、入射波長が共鳴波長に近づくにつれて急激に増加します（図2c、f、i）。キャリア散乱時間τ キャリア移動度μを決定します グラフェンでは、フェルミ速度がνの\（\ tau ={\ mu \ mu} _c / e {\ nu} _F ^ 2 \） _F =9.5×10 ⁴ MS。 μのキャリア移動度を考慮すると> 10m ² V ^-1 s ^-1 高品質の懸濁グラフェン[32]で実験的に達成されており、τにつながります。> 1.5 ps、τの設定 ≤0.5psは、グラフェンの実際の輸送損失を控えめに反映できます。 τ 、キャリア移動度μに関連付けられています 、Re（ n に優しく影響します _eff ）およびFF GPの励起波長ですが、Im（ n _eff ）および吸収（図2a–c）。強化されたμ _c Re（ n _eff ）およびIm（ n _eff ）同時に、したがってFF GPの共振波長をそれに応じて減少させます（図2d–f）。 Re（ n _eff ）、Im（ n _eff ）、およびFF GPの共振波長は、グラフェン層の数に対応して、グラフェンの厚さが増加するにつれて減少します（図2g–i）。

以下では、τを取り上げます。 =0.5ps、μ _c =0.65 eV、および d _g 例として=1nm。 GSSDG上のGPの分散関係を図3aに示します。ここで、計算された分散曲線は、商用ソフトウェアLumerical FDTDSolutionsによって得られたシミュレーション結果とよく一致しています。図3bは、シリコン格子がある場合とない場合のグラフェンシートの光学応答を示しています。 λでは吸収効率（20％以上）が大幅に向上していることがはっきりとわかります。 =格子が含まれる場合は28.62μm（ p =4μm）。対照的に、グレーティングが考慮されていない場合、吸収効率は、考慮されるスペクトル範囲全体にわたって低レベル（2％未満）に保たれます。前者の場合の著しく増強された吸収は、λでのGPの励起に起因する可能性があります。 =28.62μm。 | E から見つけることができます | λでの分布 =28.62μm（図3c）、励起されたGPが基本的な誘導波共振モード（ j ）であること =1）。図3dから、数値シミュレーションからの格子周期に関する基本モードの共振波長は、式（1）によって予測された理論結果とよく一致していることがわかります。 （6）。

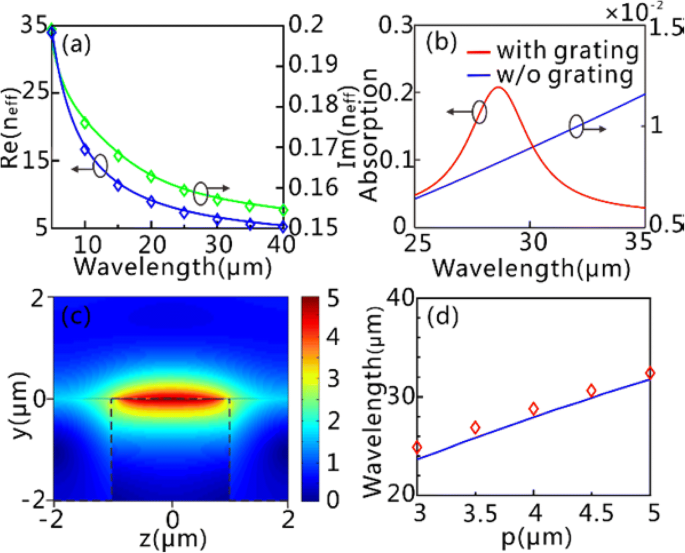
GSSDGでのFFGPとフィールド拡張。 a GSSDG上のGPの分散曲線。青と緑の実線は実際の[Re（ n _eff ）]および虚数[Im（ n _eff ）]式から取得した実効インデックスの一部。 （3）、それぞれ、青と緑のひし形は数値シミュレーションから得られます。 b 回折格子基板のある吸収スペクトル（赤い線）と回折格子のない純粋なシリコン基板（青い線）。 c 正規化された| E | 28.62μmでの基本的なGPモードの分布。黒い破線はシリコン層の輪郭を描いています。 d 基本GPモードの励起波長とグレーティング周期の関係。青い線は式から取得されます。 （6）、そして赤いひし形は数値シミュレーションからのものです。 b で および c 、 P 4μmに設定されています。すべてのシミュレーション結果は、商用ソフトウェアLumerical FDTDSolutionsによって取得されます

FF GPの群速度の大幅な低下（空気中の光速の数十分の1）により、グラフェン表面で大幅に強化されたプラズモン場が発生することに注意してください。プラズモニック場は、照明平面波の5倍の電界増強を受けます。これは、グラフェンの大きな3次光学非線形性と組み合わせて、CEが大幅に増強されたTHF GPを生成することが大いに期待できます[16、17]。グラフェンの非線形応答は、[17]として定義される非線形伝導係数で表すことができます。

ここで、フェルミ速度ν _F =9.5×10 ⁴ m / s。

THFGPの生成

次に、グラフェンシートが格子の有無にかかわらず維持されている場合のグラフェン表面上のTHFGPの電界強度を比較します。 FDTDシミュレーションの境界条件は、図1および2で使用されたものと同じです。グラフェンシートが0.11MW / cmの電力密度の法線入射連続波（CW）光で照射された場合の、波長の関数としての正規化電界強度（NEFI）を図4aに示します。 ² 中心波長は28.62μmです。ここで、NEFIは、電界強度を格子構造で28.62μm（FF）の値に正規化することによって得られます。格子が含まれていないNEFIスペクトルと比較して、格子構造のあるNEFIスペクトル（GSSDG）のTHFで見かけのピークが発生していることがわかります。 CEを\（{\ int} _0 ^ p {P} _y ^ {THF} dz / \ left（{P} ^ {FF} p \ right）\）として定義します。ここで、\（{P} _y ^ {THF } \）は y です THFでのポインティングベクトルの成分、および P ^FF は入射光のパワー密度であり、CEは5.71×10 ^-7 に達します。 GSSDGの場合。 FF GPの励起は、THFGPのCEの向上に寄与することは容易に推測できます。 E の実数部のフィールド分布 _y 図4bに示すTHFで、グラフェン表面でのTHFGPの生成を検証します。

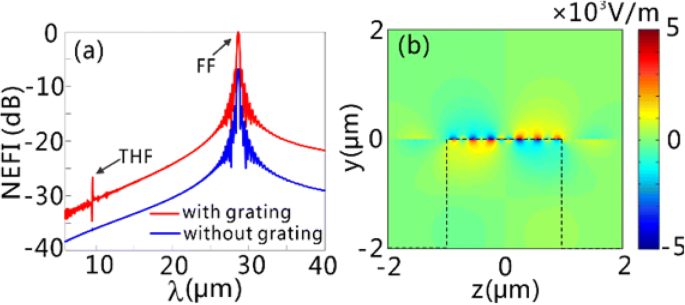
GSSDGでのTHFGPの生成。 a 0.11 MW / cm ² の電力密度のCW光で通常照らされる格子がある（赤い線）およびない（青い線）構造のNEFI 中心波長は28.62μmです。赤い線の2つのピークは、FF GP（λ）を示します。 =28.62μm）および生成されたTHF GP（λ =9.54μm）、それぞれ。 b E の実数部の分布 _y 生成されたTHFGPの場合。 b の黒い破線 シリコン層の輪郭を表します。 GSSDGの構造パラメータは図3と同じです

中赤外シリコンフォトニクスの光源としてのGSSDG

次に、GSSDGプラズモン波長コンバーターを使用して、シリコン集積フォトニック回路に直接光源を提供することを検討します。図5aに示す例として、2つのグラフェン-シリコンプラズモン導波路（GSPW）が両側のGSSDGに取り付けられています。 GSPWは、FFおよびTHFGPをカバーする広いスペクトル帯域でGPをガイドできるように選択されます。 GSSDGのFFおよびTHFGPモードのモードフィールド分布（グラフェン表面に対して非対称）は、GSPWでサポートされているGPモードと強い類似性を示すため、格子セクションが通常の入射で照らされると、次のように推測できます。 FF波、グレーティング領域上に生成されたFFおよびTHF GPは、両側のGSPWに効率的に結合できます。予測を検証するためにFDTDシミュレーションを実行しました。完全一致レイヤー境界は、両方の y で使用されます および z モデリングの方向。グレーティングセクションに衝突する法線入射FF光波をシミュレートし、FFおよびTHF GPの電界分布を示しました（図5b、c）。シミュレーションでは、グレーティングセクションのみが入射光で照らされるようにするために、全視野/散乱視野光源が使用されます[33]。完全に一致した吸収境界を使用して、計算領域の境界に到達するすべての光波を完全に吸収しました。図5bは、FF GPがグレーティングの上のグラフェン表面で励起され、両側のGSPWに沿って伝播することを示しています。図5cから、グレーティングセクションとGSPWの両方で、グラフェン表面のTHFGPの外観をさらに確認できます。ここで、CEは次のように定義されます

ここで、\（{P} _z ^ {\ mathrm {THF}} \）は z です。 -THFでのポインティングベクトルの成分、\（\ int {P} _z ^ {\ mathrm {THF}} \ mathrm {dz} \）は、GSPWにおけるTHFGPの出力電力密度 P > ^FF は入射FF光波のパワー密度であり、 N _p はグレーティング周期の数です。図5dから、THGのCEが最大値3.68×10 ^-7 に達していることがわかります。 （− 64.3 dB）格子境界で、グラフェンからのオーム吸収損失により、伝搬方向に沿って指数関数的に減衰します。

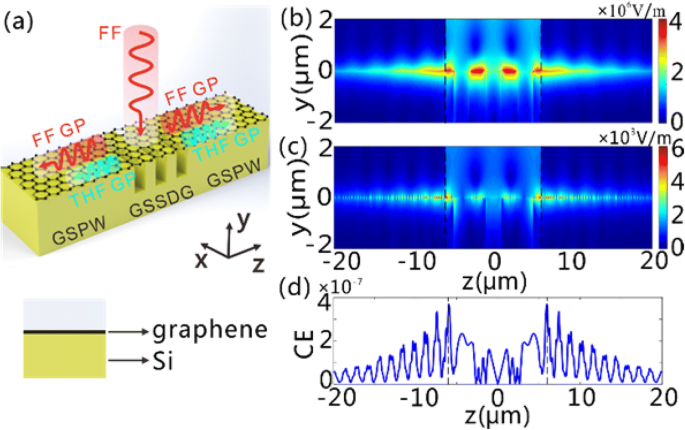
GSSDGおよび接続されたGSPWでのFFおよびTHFGPの生成。 a FFの法線入射x偏波平面波が構造を照らしているときのGSSDGと両側の接続されたGSPWの概略図。 FF GPがGSSDGで励起された後、THF GPが生成され、2つのGSPWに沿ってガイドされます。 GSPWの断面は下のパネルに示され、グラフェンシートとSi層が示されています。 b 、 c | E | b の分布 FFと c y のTHFGP - z グレーティングセクションとしての平面は、0.19 MW / cm ² の電力密度のCW光で照らされます。 28.62μmで。 d z に沿ったTHGのCE 方向。 b の黒い破線 – d GSSDGとGSPW間のインターフェイスを表します。 b で – d 、 N _p 3に設定されています

THG波長変換器のデバイス性能を評価するための鍵となるTHGCEに影響を与える要因について説明することが重要です。 THGプロセスの場合、比較的小さなポンプ出力で最大のCEを達成することが常に期待されます。以前の研究では、3次非線形材料の局所場強度を増加させると、ポンプ出力が大幅に低下し、THGのCEが著しく改善されることが示されました[3、4、7]。図6aは、入射光波のパワー密度がGSPWの最大CEに及ぼす影響を示しています。これは、パワー密度とともに増加します。最大CEは3.68×10 ^-7 に達することに注意してください 入射光波のパワー密度が0.19MW / cm ² と低くても 、これは同じスペクトル帯域内のものよりも6〜7桁小さい[22、23]。図6bに、使用されたグレーティング周期の数 N を示します。 _p 、GSPWのCEにも影響します。 N の場合 _p が増加すると、グラフェン吸収によって引き起こされる伝搬損失が増大するため、グレーティングの中央で生成されたTHFGPの還元部分がGSPWに到達します。それにもかかわらず、 N に関連する入力電力 _p 、線形拡張を示します。したがって、THF GPの最大CEは、 N の増加とともに減少します。 _p 。ここで、THF GPの絶対出力電力密度は、入射電力密度が固定された後、実際のアプリケーション用のTHG波長コンバーターの設計をガイドするためにより意味があるはずであることを強調します。 THFGPの最大CEは N にありますが _p =2この場合、THGの出力電力密度は N のときの最大値に近似します。 _p ≥3（図6b）。したがって、GSPWでのTHF GPの生成を実証するために、3周期のグレーティングを採用しました。現在の設計での将来の実験的実装のために、入力FFソースの面積はグレーティング領域を超え、異なるグレーティング数でTHFGPを生成するときに一定に保たれます。この場合、CEは次のように記述する必要があります

ここで、FFソースの領域 S 、は一定です。したがって、出力電力密度はCEに比例するため、THF GPの出力電力密度を最大化するには、最適な格子数を適切に選択する必要があります。

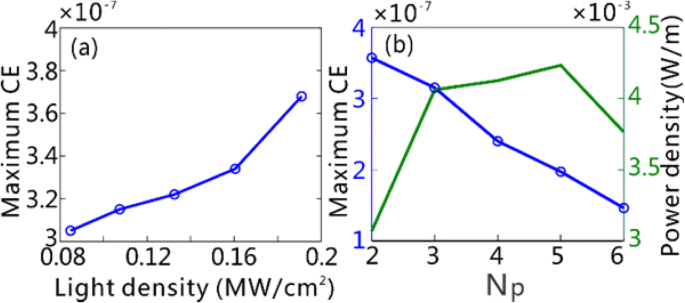
a N の入射電力密度の関数としてのTHGの最大CE _p =3. b グレーティング周期数の関数としてのTHGの最大CEおよび最大出力電力密度 N _p それぞれ使用されます。入射電力密度は0.11MW / cm ² に固定されています

グラフェンの物理的特性は、図5aに示す調査対象の構造の準備ができたら、THFGPのデバイス性能にも影響を与える可能性があります。フェルミエネルギー、μ _c 、およびグラフェン層の数は、FF GPの共振波長を大幅に変更し（図2f、i）、したがって、THFGPの生成波長にも影響を与えます。対照的に、τ 、キャリア移動度μに関連付けられています 、FFGPの共振波長とTHFGPの生成波長にはほとんど影響しません（図2c）。ただし、FFGPとTHFGPの伝搬損失は、はるかに大きなτを使用することで減らすことができます。 （図2b）、これにより、THFGPのCEが著しく増加します。 μのキャリア移動度を考慮すると> 10m ² V ^-1 s ^-1 （τ> 1.5ps）は実験[32]で達成可能であり、シミュレーション結果（τ （図3、4、5、および6）に示されている=0.5ps）は、図5aのTHFGPジェネレーターのデバイス性能を控えめに表すことができます。

最後に、デバイスの性能に対するグラフェンシートの表面粗さの影響について説明する価値があります。グラフェンの表面粗さはプラズモンを散乱させる可能性があるため、プラズモンの損失が増大します[34]。図5に示す提案されたTHFGPジェネレーターは、現在のマイクロ/ナノ製造技術に基づいて製造することができます。最初に、270 nmの厚さのポリメチルメタクリレート（PMMA）をシリコン基板上に回転させることができます。 PMMA層は、その後の電子ビームリソグラフィープロセスの後にMIKE \ IPAで現像されます。その後、電子ビーム蒸着蒸着法により、レジスト上に厚さ60nmのCr層を蒸着します。シリコン格子基板は、誘導結合プラズマ装置などのエッチング技術で形成することができます。続いてウェットエッチング法により、残留Cr層をウェットエッチング法により除去する。最後に、グラフェンシートがシリコン格子に転写され、図5に示す最終構造を形成します。

結論

中赤外および遠赤外領域で法線入射平面波を使用して、シリコン格子上のグラフェンシートでTHFGPが生成されることを数値的に示しました。グラフェン表面でTHFGPが生成および伝達され、グラフェンの大きな3次非線形感受性と組み合わせて励起されたFF GPの電界強度が大幅に増加するため、CEが劇的に向上することが示されました。生成されたTHFGPは、GSPWに便利に結合できます。これにより、シリコンプラットフォームへのグラフェンベースの波長変換器の統合が大幅に容易になります。私たちの提案は、シリコンプラットフォーム上で中赤外線および遠赤外線フォトニクス用のグラフェンベースの光源を作ることを刺激し、信号処理、分光法、センシングなどのシリコンフォトニクスの機能を広げることができます。

略語

CE：

変換効率

CW：

連続波

FDTD：

有限差分時間領域

FF：

基本周波数

GP：

グラフェンプラズモン

GSPW：

グラフェン-シリコンプラズモン導波路

GSSDG：

誘電体格子によって支えられたグラフェンシート

PMMA：

ポリメチルメタクリレート

THF：

3次高調波周波数

THG：

第三調和世代