2つの転位した平行金属格子におけるダイクロイック光ダイオード伝送

はじめに

光子を一方向に透過し、逆方向への透過を禁止する光ダイオードは、一方向の透過特性により大きな注目を集めています[1]。光と物質の相互作用の時間反転対称性が破られると、光ダイオード現象が観察されます。外部磁場[2]、バイアス電圧[3]、音波[4]、または時間依存変調[5、6]を適用して、光ダイオード効果を実現できます。さらに、非対称多層構造[7]、非対称フォトニック結晶[8]、非対称格子[9]など、空間反転対称性の破れの構造は別の選択肢です。ここ数十年で、金属マイクロナノ構造は、表面プラズモン（SP）の有望な特性のために大きな関心を集めました。プラズモニックデバイスは、メタ表面ホログラフィー[10,11,12,13,14]、屈折率センサー[15、16]、フィルター[17、18]などの多くの研究分野で提案されています。プラズモニックデバイスは、ナノスケールの電磁場の相互作用を強力に変更できます[19]。 SPの変調は、周囲の誘電環境と金属構造の幾何学的パラメータを変更することで実現できます[20、21]。ナノスケールの金属構造で構成される光ダイオード、例えば、プラズモン層サンドイッチ格子[22、23]、カスケードプラズモン格子[24、25]、プラズモンナノホール[26]、プラズモンスロット導波路[27]、およびプラズモンナノ粒子凝集体[28]。 、光学情報処理の目的で広く研究されています。

この論文では、ダイクロイック光ダイオードの透過率は、誘電体スラブを挟む2つの転位した平行な金属格子で得られます。狭いスリットからなる金属格子は異常な光透過を示し[29、30]、非対称構造は一方向透過を実現するため[27、28、29、30]、透過の向上と高い分離コントラスト比の両方が逆透過方向の2つの動作波長帯で達成されます。 、31]。照射順序に従って、異なる格子定数を持つ2つの金属格子がそれぞれセレクターとエミッターとして機能します。セレクターはSPを励起して共鳴波長を選択し、SPの寄与によりエミッターは光の透過を実現します。入射方向が逆になると、2つのグレーティングの役割が交換され、SPが別の波長で励起されます。したがって、ダイクロイック光ダイオード透過が得られる。この論文で提案されている光ダイオード構造の厚さは、160nmと非常に薄いです。ナノファブリケーション技術の開発により、紫外線ナノインプリントリソグラフィー[32]、レーザー直接書き込みリソグラフィー[33]、電子ビームリソグラフィー[34]など、多くの方法を金属格子構造の製造に適用できます。光ダイオードの特性は、入射強度に依存しません。これらの特性は、私たちの構造が光学的統合において幅広い可能性を秘めていることを意味します。

メソッド

光ダイオード構造のスキームを図1に示します。構造は2つの銀格子 G で構成されています。 ₁ および G ₂ シリカ層を挟む。シリカ層の厚さは d で表されます。 。 G ₁ および G ₂ スリット幅が同じ s 、同じ厚さ h 、およびさまざまな格子定数Λ _i （ i =1、2）。構造は並進対称であり、ユニットセルには2ユニットの G が含まれています ₁ および3ユニットの G ₂ 。 Δ G の横方向の相対位置を示します ₁ および G ₂ ユニットセル内。ドルーデモデル[35]は、銀の誘電機能を説明するために使用されます。シリカの屈折率は、分散を無視して1.5です。周囲の誘電体は空気であり、その屈折率は1です。 p の垂直入射平面波 -偏光は、光ダイオードの効果を調査するために使用されます。

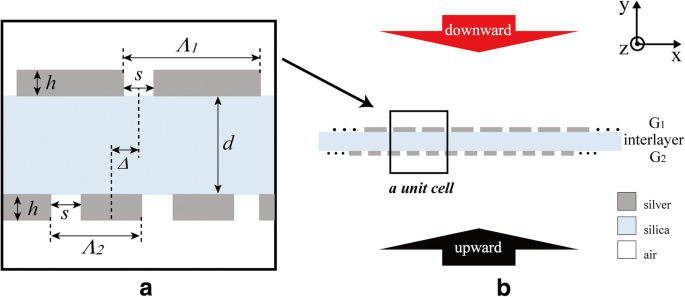
光ダイオード構造の概略図。 a ユニットセル。 b 全体像

透過率 T 光ダイオード構造の定義は次のとおりです。

ここで P _i は入射電力であり、 P _o は出力電力です。 T は、有限差分時間領域（FDTD）法を使用して数値的にシミュレートされます[36]。周期境界条件は左側と右側に採用され、完全一致層境界はシミュレーションモデルの上面と下面に適用されます。 T _D および T _U それぞれ、下向き入射と上向き入射の透過率を表します。光ダイオードの特性は、分離コントラスト比ηで表されます。 ：

したがって、η =1は最高の光ダイオード性能を意味します。

結果と理論的分析

光ダイオード構造の透過率とアイソレーションコントラスト比を図2に示します。 T _D T とは異なります _U 入射波長がλよりも小さい場合 _C 。 T _D 最大値0.73に達し、 T _U は3.7×10 ⁻³ λで _D （1315 nm）。一方、 T _U 最大値0.82に達し、 T _D は3.6×10 ^-4 λで _U （921 nm）。 λでの分離コントラスト比 _D およびλ _U それぞれ0.990と0.999です。図2は、λ付近で光ダイオード効果が得られることを示しています。 _D およびλ _U 、および2つの波長帯の伝送方向は逆です。ダイクロイックダイオードの動作波長帯では、構造は異常な透過率を示します。

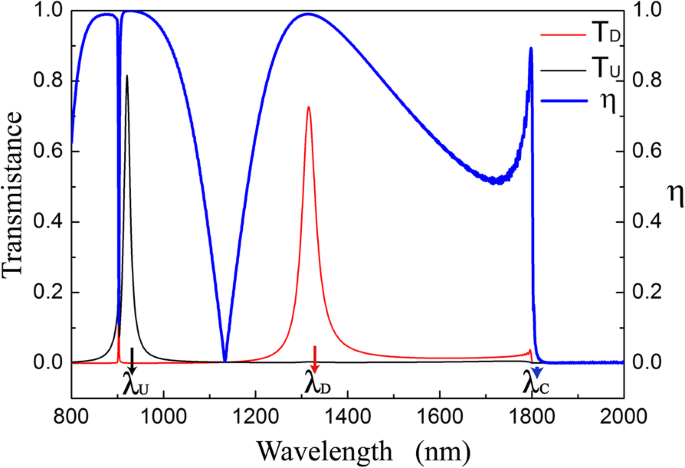
d の光ダイオード構造の透過スペクトルと分離コントラスト比 =200 nm、 s = h =50 nm、Λ ₁ =900 nm、Λ ₂ =600 nm、およびΔ =0 nm

ダイクロイック光ダイオードの透過率を理解するために、電界強度| E | ² 2つの動作波長帯でシミュレーションされます。図3a、dに示すように、光が光ダイオード構造を透過すると、2つのグレーティング間の電界が増強されます。一方、図3b、cは逆ブロッキング状態を示しています。 2つのグレーティング間の電磁界の増強は、2つの隣接する銀/シリカ界面のSPによるものです。 2つのグレーティングのSPのタイプは異なり、それぞれ構造化SP（SSP）と誘導SP（ISP）に分類されます。 SSPは励起され、最初に照射されたグレーティング（セレクター）で生成されます。 ISPは、SPPと隣接する銀/シリカ界面との間の結合によって後者のグレーティング（エミッタ）で誘導されます。 SSPとISPにより、光は光ダイオード構造を透過します。

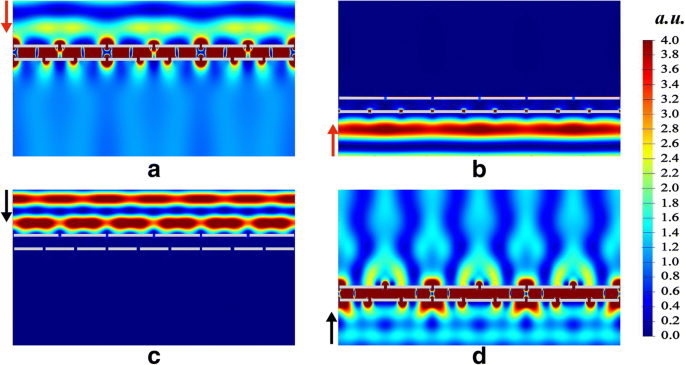
電界強度の分布| E | ² λでの下方入射の場合 _D =1315 nm（ a ）、λでの上方入射 _D =1315 nm（ b ）、λでの下方入射 _U =921 nm（ c ）、およびλでの上方入射 _U =921 nm（ d ）

銀/シリカ界面および E の表面電荷密度 _y 電界分布の成分を図4に示し、SPの結合機能を示します。図4aでは、 G ₁ および G ₂ 隣接する表面に反対の電荷があります。これは平板コンデンサに似ています。下向きの入射の条件下で、 G ₁ λでSSPを励起するセレクターとして機能します _D 。周期的な表面電荷密度分布は、SPPが G の格子定数によって決定されることを表しています。 ₁ 。 G ₂ SPPによって誘導されるISPをサポートし、送信用のエミッターとして機能します。 E _y G の間 ₁ および G ₂ 図4bに示すように、SPPとISP間の結合により強化されます。図4c、d、 G に示す上向きの入射状態の場合 ₂ セレクターおよび G として機能します ₁ エミッターとして機能します。

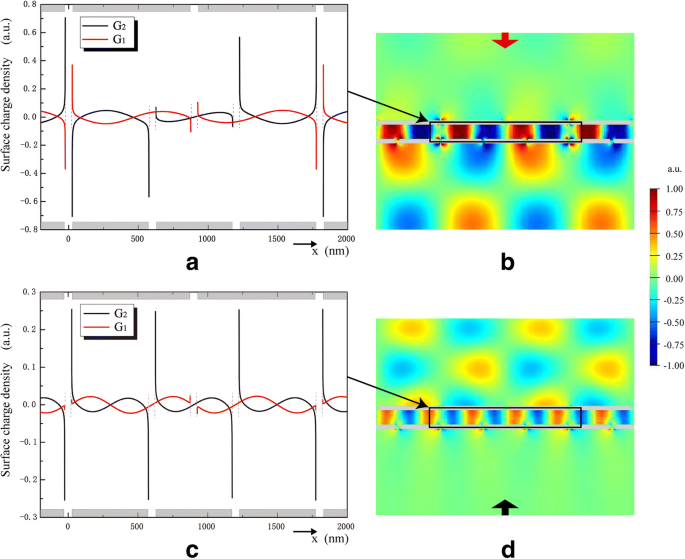
G での銀/シリカ界面の表面電荷密度 ₁ および G ₂ 、λでの下方入射の条件下 _D =1315 nm（ a ）およびλでの上方入射 _U =921 nm（ c ）。 Ey λで下向きに入射する条件下での電界の成分 _D =1315 nm（ b ）およびλでの上方入射 _U =921 nm（ d ）

図4からわかるように、透過場は周期的であり、水平方向（ x ）で不均一です。 -軸）方向。期間Λ （Λ =2 Λ ₁ =3 Λ ₂ ）送信フィールド分布の）は、一体型光ダイオード構造によって変調され、2π/ Λを満たします。 =| g ₁ -g ₂ |、ここ g _i G _i の格子ベクトルです （ i =1、2）。 SPが存在するため、グレーティングの回折効率が向上します。横波数ベクトルκ 透過光の量は g の重ね合わせに由来します ₁ および g ₂ ：

そして、それは臨界波長λを決定します _C （λ _C =2π/ |κ|） T の場合 _D ≠ T _U 。式によると。 （3）、λ _C 上記の構造では1800nmであり、シミュレーション結果λとよく一致しています。 _C =1806nmを図2に示します。光ダイオードの効果はλの範囲で現れます。 ≤λ _C 。シミュレーション結果によると、統合されたグレーティングの周期（1800 nm）は、ダイオードの動作波長（1315nmおよび921nm）よりも大きくなっています。多次回折成分は、統合された格子からの光散乱で得ることができます。したがって、光が遠方界に透過されたとしても、透過場は格子に平行な方向に沿って均一ではありません。

銀格子のSSPは、SSPが放射モード[37]であるのに対し、SPが完全に表面結合モードであることを除いて、平面銀/シリカ界面のSPと同様です。 SSPは、ほぼ格子のスリットが非常に狭い場合に、平面銀/シリカ界面のSPとして扱うことができます。したがって、SSPの分散関係は、[38]のように書くことができます。

ここで k ₀ は自由空間の波数ベクトルであり、ɛ _m およびɛ _d はそれぞれ銀とシリカの誘電係数です。式（1）で表される分散関係。 （4）を図5に示します。この論文のドルーデモデルパラメータ[35]を使用して計算された分散曲線は、光子エネルギーが2.75 eV（λ> 450 nm）。図5では、赤と黒の縦の破線は| g を表しています。 _{1 |} および| g ₂ |、それぞれ。ベクトルマッチング条件[40]が満たされると、SSPはグレーティングによって励起されます。

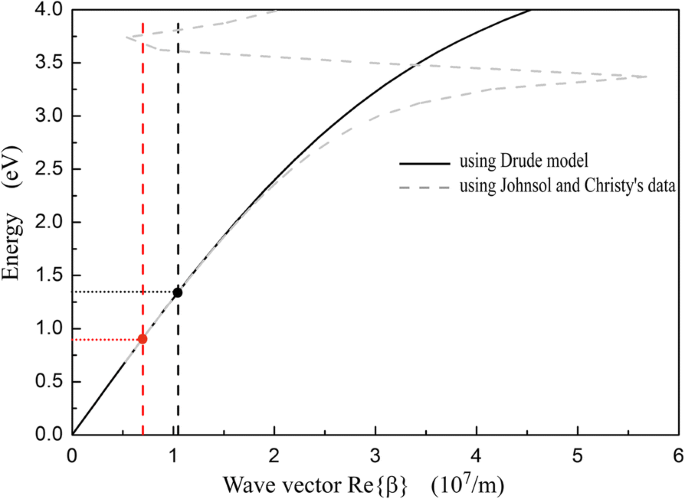
ドルーデモデルとジョンソンおよびクリスティの光学定数データを使用して計算された平面銀/シリカ界面でのSPの分散。赤と黒の縦の破線は、格子ベクトル係数| g を表します。 ₁ |および| g ₂ |、それぞれ

法線入射の場合（θ =0°）、1次（ N =1）グレーティングの回折は、回折効率が最も高く、つまり、SSPの励起効率が最も高くなります。したがって、式。 （5）は、図5に示す赤と黒の点で満たされます：

光ダイオード構造では、G ₁ 下向きの入射と G のためにSSPを励起するためのセレクターです ₂ 上向き入射のセレクターです。 G ₁ および G ₂ 異なる格子定数を持っているため、SSPは逆入射方向に対して異なる波長で励起されます。図5では、赤い点での光子エネルギーは0.91 eV、波長は1365 nmであり、これはλに対応します。 _D （1315 nm）図2に示されています。同様に、黒い点で示される光子エネルギーは1.04 eVであり、その波長は924 nmであり、λに対応します。 _U 図2の（921 nm）。格子からプレートへの近似として、SSPの共振波長は式（1）を使用して計算されます。 （4）と式。 （6）は、図2に示すFDTD法を使用してシミュレーションしたものと正確に同じではありません。

式（5）は、入射角θを示しています。 SSPへのグレーティングの波数ベクトルマッチング条件に影響を与えます。 θの変更に伴い 、λでの透過率と分離コントラスト比 _D （1315 nm）およびλ _U （921 nm）をシミュレートし、それぞれ図6a、bに示します。 θを使用 0°から10°に増加、 T _D λで _D および T _U λで _U g 間の波数ベクトルの不一致の減少 _i およびSSP。 （ T _D λで _D θのときに0に減少します ≈40°および T _U λで _U θのときに0に減少します ≈35°。）0°≤θ≤の入射角範囲で 5°、 T _D λで _U および T _U λで _D ほぼ0であり、η 両方のλで常に0.98より大きく保たれます _U およびλ _D 。図6は、この構造がλで良好な光ダイオード効果を示すことを示しています。 _D およびλ _U 小角度の入射下で。

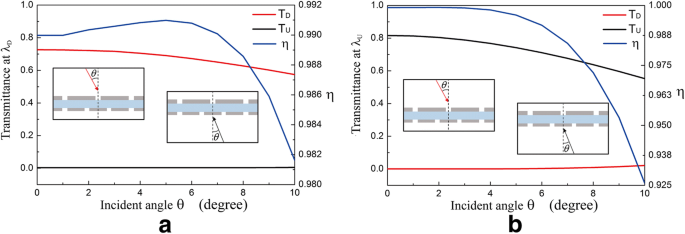
λでの透過率と分離コントラスト比に対する入射角の影響 _D =1315 nm（ a ）およびλ _U =921 nm（ b ）

調査とディスカッション

このセクションでは、透過スペクトルと分離コントラスト比に対する構造パラメータの影響を調査します。

中間層の厚さ d およびグレーティングの横方向の相対位置Δ 製造精度によって制限されます。 d の影響 およびΔ 透過スペクトルと分離コントラスト比については、図1と図2に示します。それぞれ7と8。図7は、光ダイオードの動作波長帯が d のときにわずかな赤方偏移を示すことを示しています。 増加します。一方、 T の最大値 _D 減少はほとんどありませんが、 T の最大値 _U 大幅に減少します。 d の増加 構造を通る光の透過距離を長くし、 G 間の電磁相互作用を弱めます ₁ および G ₂ 、およびエミッタの表面に誘導される電荷​​密度を損ないます。図4に示すように、エミッタのスリットコーナーに分布する電荷は、送信フィールドの電気双極子源として機能します。エミッタのスリットコーナーの電荷密度 G ₂ （図4a）は、エミッタのスリットコーナーよりもはるかに大きい G ₁ （図4c）、つまり d T の最大値への影響は少ない _D T よりも _U 。その上、 d の増加に伴い 、FP ₁ としてマークされた小さなピーク およびFP ₂ T に表示されます _U FP ₁ の透過ピーク 大きな赤方偏移を示します。電界強度| E | ² 分布は、FP ₁ およびFP ₂ ファブリペロー共鳴の結果です。

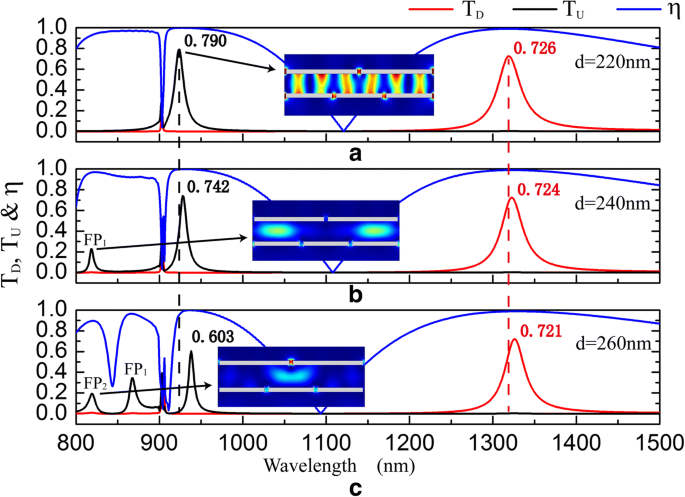
d の影響 透過スペクトルと分離コントラスト比について。 d =220 nm（ a ）、 d =240 nm（ b ）、および d =260 nm（ c ） s の場合 = h =50 nm、Λ ₁ =900 nm、Λ ₂ =600 nm、およびΔ =0nm。挿入図は電界強度の分布です| E | ² 上向きの伝送共振用

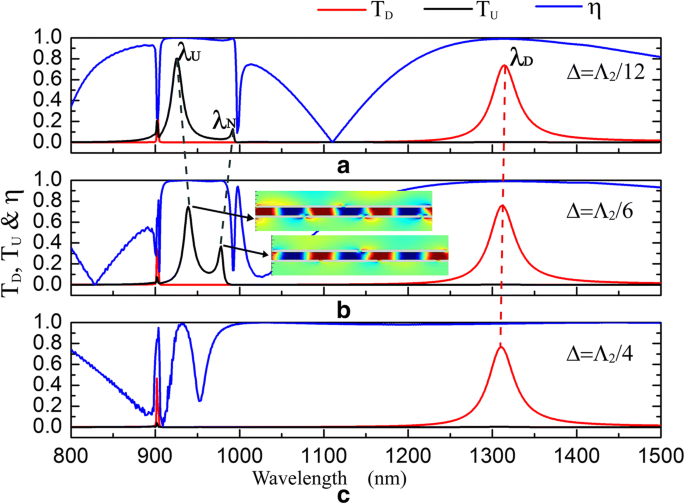
Δの影響 透過スペクトルと分離コントラスト比について。 Δ =50nm =Λ ₂ / 12（ a ）、Δ =100 nm =Λ ₂ / 6（ b ）、およびΔ =150 nm =Λ ₂ / 4（ c ） d の場合 =200 nm、 s = h =50 nm、Λ ₁ =900 nm、およびΛ ₂ =600nm。 （ b の挿入図 ）は E _y 上向き透過共振の分布

図1に示すように、光ダイオードの構造は周期的であり、Δ=a の場合は同じユニットセルを持ちます。 ±M Λ ₂ / 2（0 nm < a <Λ ₂ / 2および M =0、1、2…）。また、Δのユニットセル = a Δ=と左右対称に反転します − a ±M Λ ₂ / 2そして彼らは同じ伝達効果を実現することができます。したがって、光ダイオード構造の透過率はΔの影響を受けます。 として： T （Δ ）= T （Δ + Λ ₂ / 2） =T （− Δ + Λ ₂ / 2）。図8に示すように、λでの光ダイオード効果 〜921 nmは、Λの期間内にオンとオフを切り替えます ₂ / 2 as Δ 増加します。ただし、 T の透過ピーク _D λでわずかな青方偏移と光ダイオード効果を示します Δの場合、〜1315nmは常にオンです 増加します。図8aに見られるように、λでの新しい透過ピーク _N T に登場 _U λ付近の曲線 _U 。 Δの場合 Λから増加 ₂ / 12からΛ ₂ / 6、λのピーク _N λのピークが青方偏移を示す _U 赤方偏移を示します（図8a、b）。 E _y λでの透過共鳴の分布 _U およびλ _N 図8bに挿入されています。シミュレーション結果によると、λでの共振 _N エネルギー分割のために生成されます。 Δの場合 Λに増加します ₂ / 4、図8cに示す、 T _U が抑制され、2つの透過共振がなくなり、λで光ダイオード効果がオフになります。 〜921nm。

理論解析によれば、光ダイオードの動作波長帯は、グレーティングパラメータを最適化することにより、特定の範囲で取得できます。図9は、ダイクロイック光ダイオードの透過が、構造パラメータ d を使用して可視光範囲で達成されることを示しています。 =100 nm、Λ ₁ =450 nm、Λ ₂ =300 nm、 s = h =30 nm、およびΔ =0nm。ダイクロイックダイオード透過波長帯の最大透過率は、80％（上向き入射の場合は522 nm）と71％（下向き入射の場合は732 nm）であり、対応するアイソレーションコントラスト比η 0.998と0.993です。

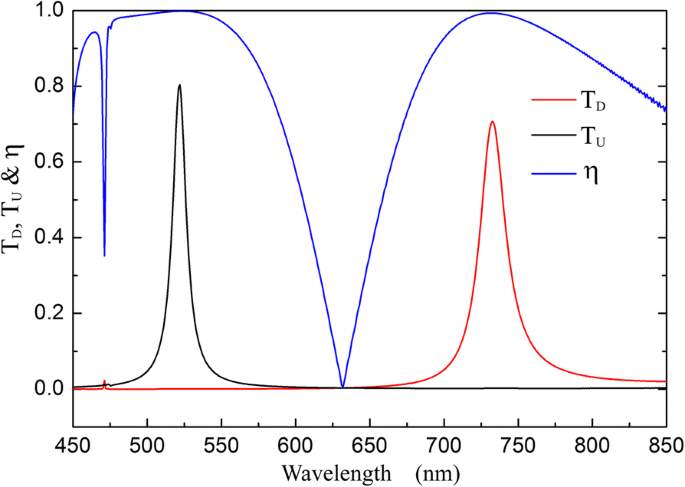
d の光ダイオード構造の透過スペクトルと分離コントラスト比 =100 nm、Λ ₁ =450 nm、Λ ₂ =300 nm、 s = h =30 nm、およびΔ =0 nm

さらに、私たちの構造のユニットセルのコンポーネントも光ダイオード現象に影響を与えます。式によると。 （5）、ダイオード効果の波長帯はΛに依存します ₁ およびΛ ₂ 。私たちの調査では、2ユニットの G で構成されるユニットセルを選択します。 ₁ および3ユニットの G ₂ 、つまり2 Λ ₁ =3 Λ ₂ 、光ダイオード波長帯で高い透過率と良好なアイソレーションコントラスト比を同時に得るために。たとえば、図10は、3ユニットの G で構成されるユニットセルを備えた光ダイオード構造のダイクロイック透過を示しています。 ₁ および4ユニットの G ₂ 。光ダイオードの効果は、 T を使用して530nmで得られます。 _U =72％および659 nm、 T _U =76％。 | g の差により、2つの波長での分離コントラスト比は0.912と0.987に減少します。 ₁ | および| g ₂ | は小さく、セレクターとして機能するグレーティングは、異なる効率で両方のグレーティングのSSPを励起できます。また、Λの場合 ₁ =2 Λ ₂ 、 G の一次回折によって引き起こされる光ダイオード構造のSP透過共鳴 ₂ G の2次回折によっても励起できます ₁ 2 g ₁ = g ₂ 、これにより、分離コントラスト比が低下します。したがって、良好な光ダイオード特性には、2つのグレーティング定数に十分な差があり、整数倍の関係を回避する必要があります。

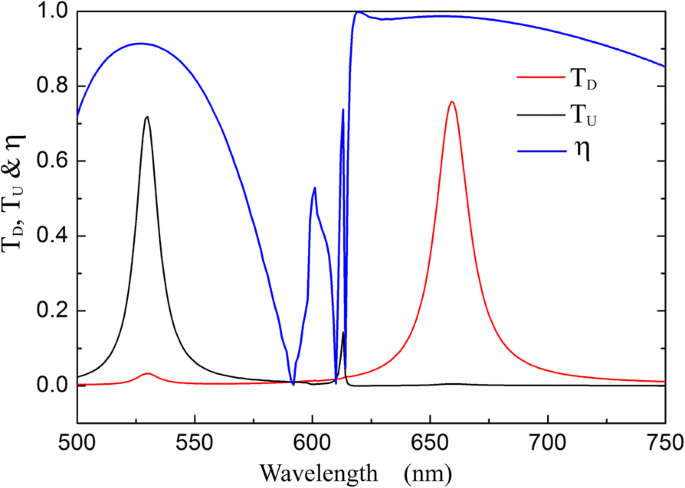
3ユニットの G を含むユニットセルを備えた光ダイオード構造の透過スペクトルと分離コントラスト比 ₁ および4ユニットの G ₂ 。 d =100 nm、Λ ₁ =400 nm、Λ ₂ =300 nm、 s = h =30 nm、およびΔ =0 nm

結論

SPに基づくダイクロイック光ダイオード伝送は、2つの転位した平行な銀格子とシリカ中間層で構成される当社の構造で実現されています。最初に照らされた金属格子は、SSPを励起することによって透過波長帯を選択し、他の金属格子は、表面電子振動を介して電磁エネルギーを前方に放出します。光の入射方向を逆にすると、2つのグレーティングの役割が交換され、別の光ダイオード透過波長帯が現れます。光アイソレータ比はほぼ1に達する可能性があります。構造パラメータを変更することにより、光ダイオードの透過波長帯をさまざまな領域に調整できます。光ダイオードの動作波長帯と透過率は、入射強度に依存しません。構造の厚さはわずか数百ナノメートルです。私たちの構造のこれらの特性は、集積回路で幅広いアプリケーションを提供します。

略語

ISP：

誘導された表面プラズモン。

SP：

表面プラズモン

SSP：

構造化表面プラズモン